高速列車型面不同磨耗狀態下的過岔性能研究分析

肖 乾，李 超，昌 超，孫加林

(1.華東交通大學 載運工具與裝備教育部重點實驗室，江西 南昌 330013；2.西南交通大學 牽引動力國家重點實驗室，四川 成都 610031；3.中國鐵道科學研究院 鐵道科學技術研究發展中心, 北京 100081)

道岔是鐵路上最易損壞的部件之一。道岔的結構比較特殊且相對脆弱，因此在研究車輛振動特性時應與正線軌道區別對待。高速列車長期在線路上運營，在牽引、制動等工況的作用下，車輪型面不可避免會發生磨耗。其中最為常見的車輪磨耗形式便是踏面圓周凹形磨耗。在列車高速運行的情況下，車輪磨耗會對輪岔以及輪軌之間的動態相互作用產生較大的負面影響，進而影響列車的動力學性能。因此研究車輪型面在不同磨耗狀態下的過岔性能，對提升高速列車運行的安全性和穩定性有積極作用。

目前，國內外學者對車輛-道岔耦合動力學開展了大量的研究工作，取得了一系列重要研究成果。文獻[1]提出Semi-Hertz接觸方法，相較于以往的方法能更精確地模擬輪岔滾動接觸作用。文獻[2-3]通過對比兩種類型的車輛模型與道岔的動態耦合關系，認為軌道為剛體時，達到了與預期一致的效果，并求出擴展頻率范圍內系統動力響應的時域解。文獻[4]通過輪岔有限元模型深入研究道岔鋼軌破壞機理，得到了影響道岔壽命最重要的兩個因素是車輛的過岔速度和車輛軸重的結論。文獻[5]為了探究不同的道岔形狀、尺寸以及車輪型面對輪岔作用的影響，利用多體動力學軟件Simpack建立了4種車輪型面和兩種道岔的模型，進行了詳細的分析。文獻[6]深入研究了鐵路道岔輪岔接觸的幾何關系，對輪岔多點接觸的計算和判斷方法進行了詳細說明。文獻[7-8]系統研究了高速鐵路和重載線路兩種道岔情況下的車岔線橋相互作用規律。文獻[9]通過仿真對比分析了單開道岔側線尖軌不同結構形式下各個輪岔作用的響應特點，為尖軌的減磨設計提供了理論依據。文獻[10]通過跡線法和有限元法研究了車輪與道岔鋼軌的磨耗問題。文獻[11]利用Simpack與Abaqus軟件聯合仿真，建立了車岔橋剛柔耦合動力學分析模型，全面分析了高速列車直向和側向經過道岔時車輛、橋梁和道岔的動力學特性。總體來看，上述研究成果推動了道岔區輪軌和車輛軌道動力學的發展。但上述研究較少涉及以下兩個方面的問題：一是車輪磨耗引起的輪岔相互作用問題；二是不同里程下磨耗型面對輪岔的作用規律。

文獻[12-15]開展了關于輪軌型面磨耗對車輛動力學、軌道動力學特性影響的相關研究工作，但關于車輪型面磨耗對車岔作用的研究相對較少。本文采用數值模擬方法，采用多體動力學軟件UM, 以350 km/h客運專線60 kg/m鋼軌18號高速道岔和國內某型號高速列車為研究對象，建立車輛-道岔耦合動力學模型，考慮不同里程下的車輪磨耗型面，利用輪軌非橢圓多點接觸算法，系統研究不同等級速度下通過18號高速可動心軌道岔的振動特性。

1 變截面道岔模型與車輪型面磨耗實測分析

1.1 變截面道岔模型

圖1所示為單開道岔，單開道岔結構包括撤叉區、轉轍區和連接部分。高速列車在單開道岔線路行駛時，鋼軌截面是實時變化的，同時鋼軌的結構特性如高度、廓形、軌頂寬度也會實時變化。鋼軌結構的不斷變化，不可避免會增加鋼軌的振動。如圖2、圖3所示，通過輪軌型面測量儀得到高速鐵路線路道岔各處截面的數據，將得到的數據通過擬合處理獲得道岔的空間結構外形。變截面鋼軌的擬合處理示意圖如圖4所示，在變截面道岔模型中對鋼軌截面形式變化等非線性特征進行了考慮。在建模過程中還參考了18號道岔的現實尺寸情況，創建了完整的右開道岔swt格式文件。 18號道岔各關鍵截面參數見表1。

圖1 道岔區間示意圖

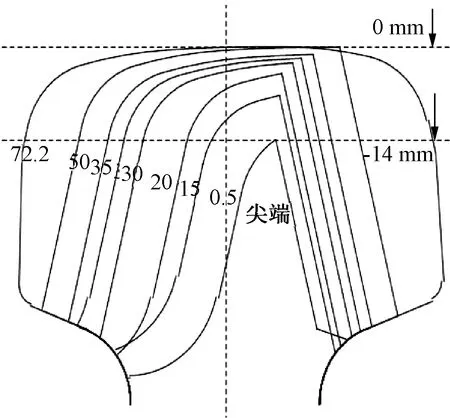
圖2 尖軌CAD圖示

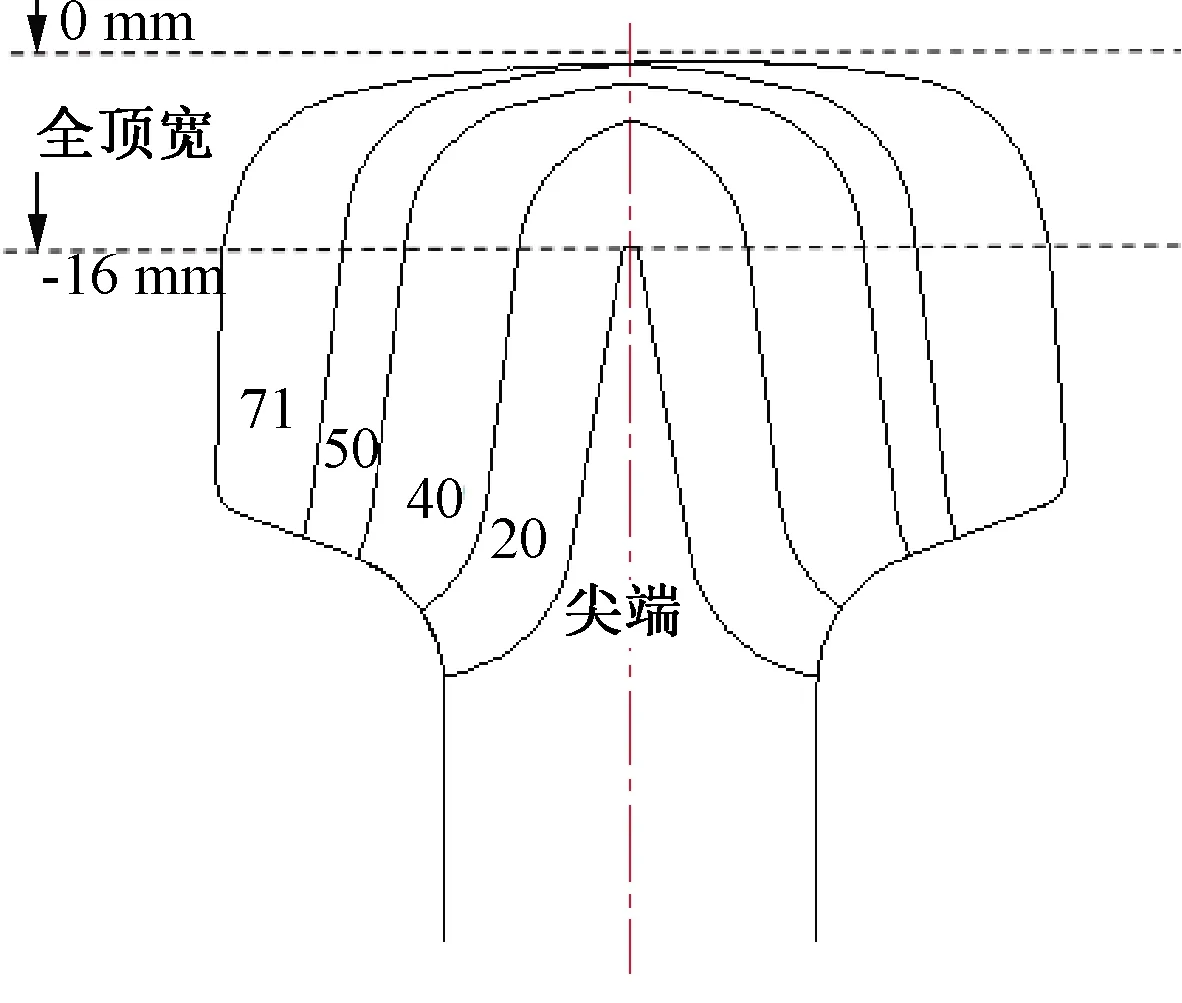
圖3 心軌CAD圖示

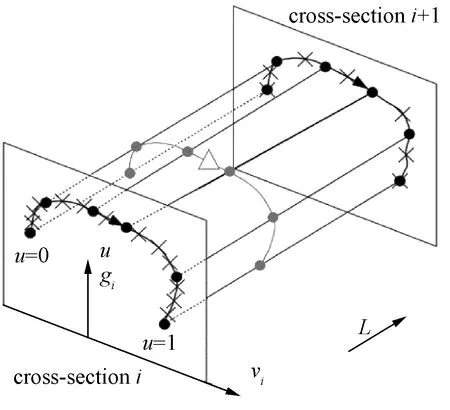
圖4 變截面鋼軌擬合示意

1.2 車輪型面跟蹤實測與磨耗特性分析

通過對該型號動車組車輪型面的磨耗情況進行跟蹤實測(圖5、圖6)，選取測試的運營里程數分別為11.6萬、15.3萬、20.8萬、25.3萬km，平均間隔里程約5萬km。規定距輪緣內側70 mm處為車輪圓周磨耗數值的測量位置。所測試的4個運營里程階段的車輪磨耗深度見表2。將現場實測型面曲線與初始型面曲線(圖7)進行對比，可以得出車輪的磨耗主要分布在兩個區域：輪緣直線區域和名義滾動圓附近區域。

表1 18號高速道岔變截面鋼軌各關鍵截面參數 mm

型面磨耗的分布范圍與運營里程數關系不大且基本固定；磨耗深度和運行里程關系較大，運行里程越大磨耗越深。車輪的輪緣位置處有輕微的磨耗且主要的磨耗形式為圓周凹形磨耗[12]。

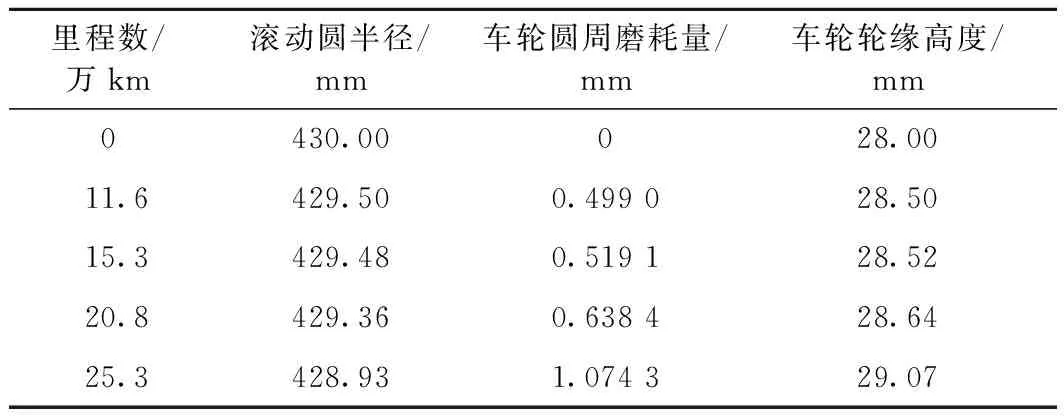
表2 車輪型面磨耗情況統計

圖5 車輪型面現場測試

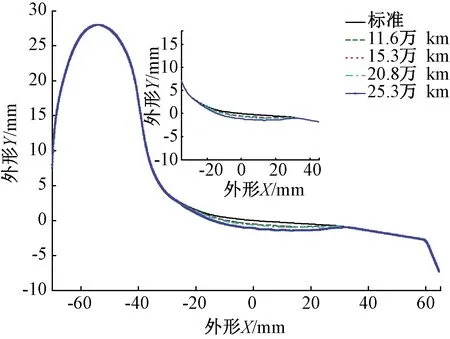
圖6 LMA實測不同運營里程下的磨耗型面

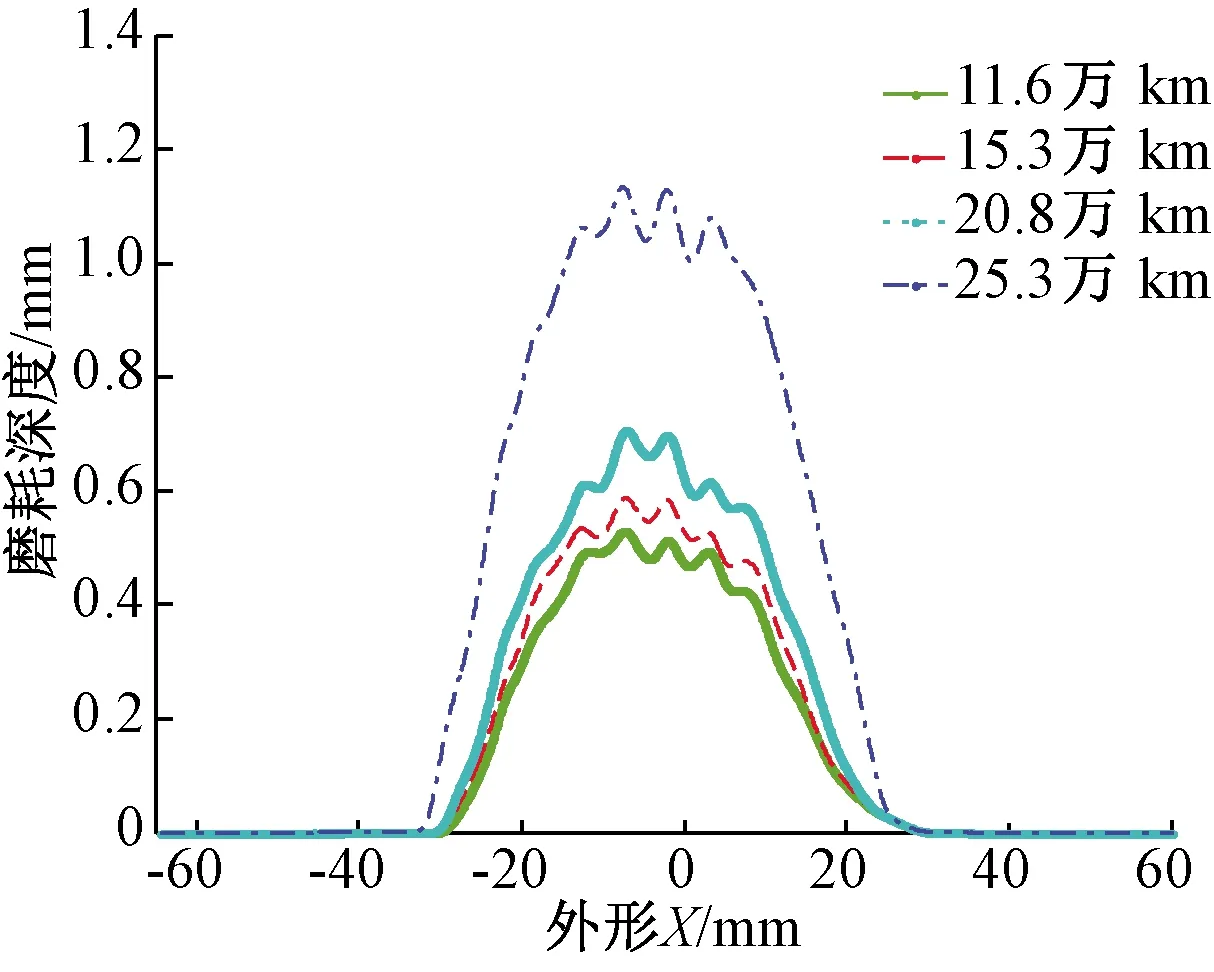
圖7 車輪型面不同位置磨耗深度示意

2 車輛-道岔耦合動力學模型

2.1 車輛系統動力學模型

在動力學軟件UM中建立50自由度的高速列車車輛模型，模型中共15個剛體，剛體的種類、數目以及各剛體的自由度見表3。在利用UM軟件建模時，彈簧、減振器等元件均忽略了其質量，以力元的形式代替。例如空氣彈簧使用的力元為Bipolar force，同時綜合考慮阻尼；一系鋼簧使用的力元為Linear force；轉臂節點使用的力元為Special force。動力學模型使用的基本軌為CHN60鋼軌，車輪踏面類型為LMA。將擬合處理好的道岔線型輸入至UM軟件中，圖8所示為建立好的車輛-道岔耦合動力學體系。

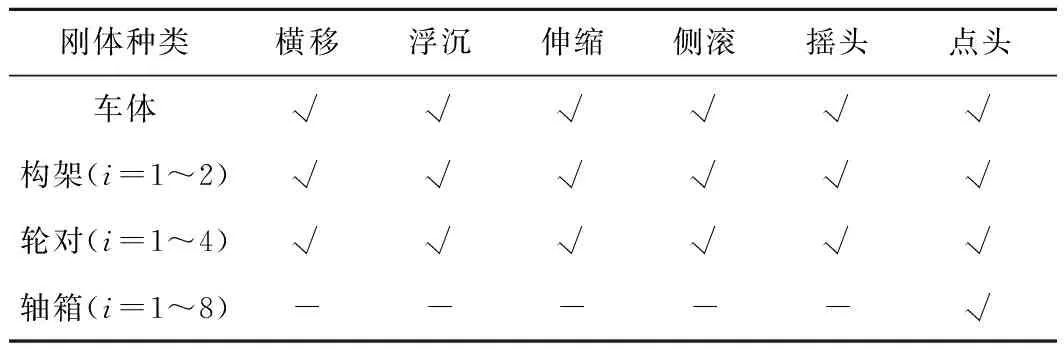
表3 剛體種類及自由度

圖9 無磨耗型面與磨耗型面輪岔接觸特性對比

圖8 車輛-道岔耦合動力學模型

2.2 輪軌滾動接觸力學模型

研究表明，列車在轉轍區域行駛過程中，將會由開始的基本軌緩慢過渡至尖軌。同時為使列車安全平穩駛過道岔，鋼軌的結構會隨著行駛狀態的改變而變化。圖9(a)、圖9(c)為初始型面頂寬分別為30、50 mm的接觸點分布圖。圖9(b)、圖9(d)為運行25萬km，頂寬分別為30、50 mm的磨耗型面接觸點分布圖。從圖9可知，輪軌型面磨損時，輪軌接觸部分容易發生多點接觸。由于接觸斑區域內的車輪和鋼軌曲率不是常數，不再滿足赫茲接觸理論的假設條件[16-17]。為更準確模擬輪軌接觸狀態，同時滿足工程上計算效率的需求，本文采用文獻[16]提出的基于虛擬滲透法的輪軌非橢圓多點接觸算法(簡稱K-P算法)。

K-P算法中考慮輪軌接觸的法向接觸應力pz為

( 1 )

滲透區域的函數為

( 2 )

h(y)=zw(y)-zr(y)

( 3 )

式中:δ0為滲透量；h(y)代表x=0界面上輪軌型面曲線zw(y)、zr(y)兩點間距離。接觸斑近似服從

( 4 )

由此可通過積分得到

( 5 )

其中，yl表示在y方向的接觸斑邊界。

則(0,0)處的法向變形位移w0為

( 6 )

可知(0,0)處的滲透值為δ0=2w(0,0)=2w0，由此可得

( 7 )

( 8 )

如圖10所示，若輪軌處發生多點接觸，根據接觸點的滲透量δ0、δi，可求解出輪軌法向力N1、Ni。

計算出輪軌接觸的法向接觸力以及間隙量后, 可以利用FASTSIM算法得出任意輪軌接觸區域上的切向蠕滑力。以80 km/h側向過岔作為研究對象，分別應用CONTACT、FASTSIM、K-P三種算法進行對比計算。根據圖11、圖12以及表4的計算結果可知，K-P算法的計算結果精度高，同時通過計算統計可知，K-P算法的計算效率比CONTACT算法高。從數值分析可知，K-P算法和CONTACT算法的計算結果相近。

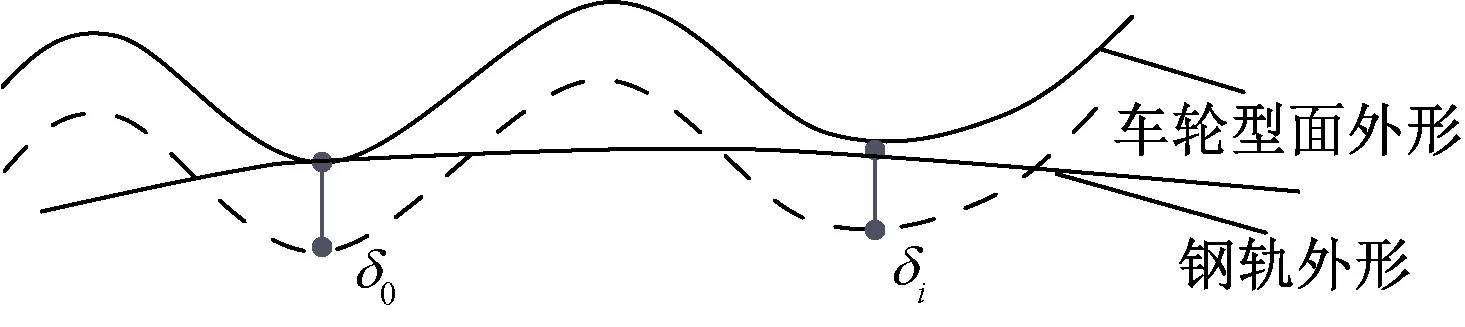
圖10 輪軌多點接觸示意圖

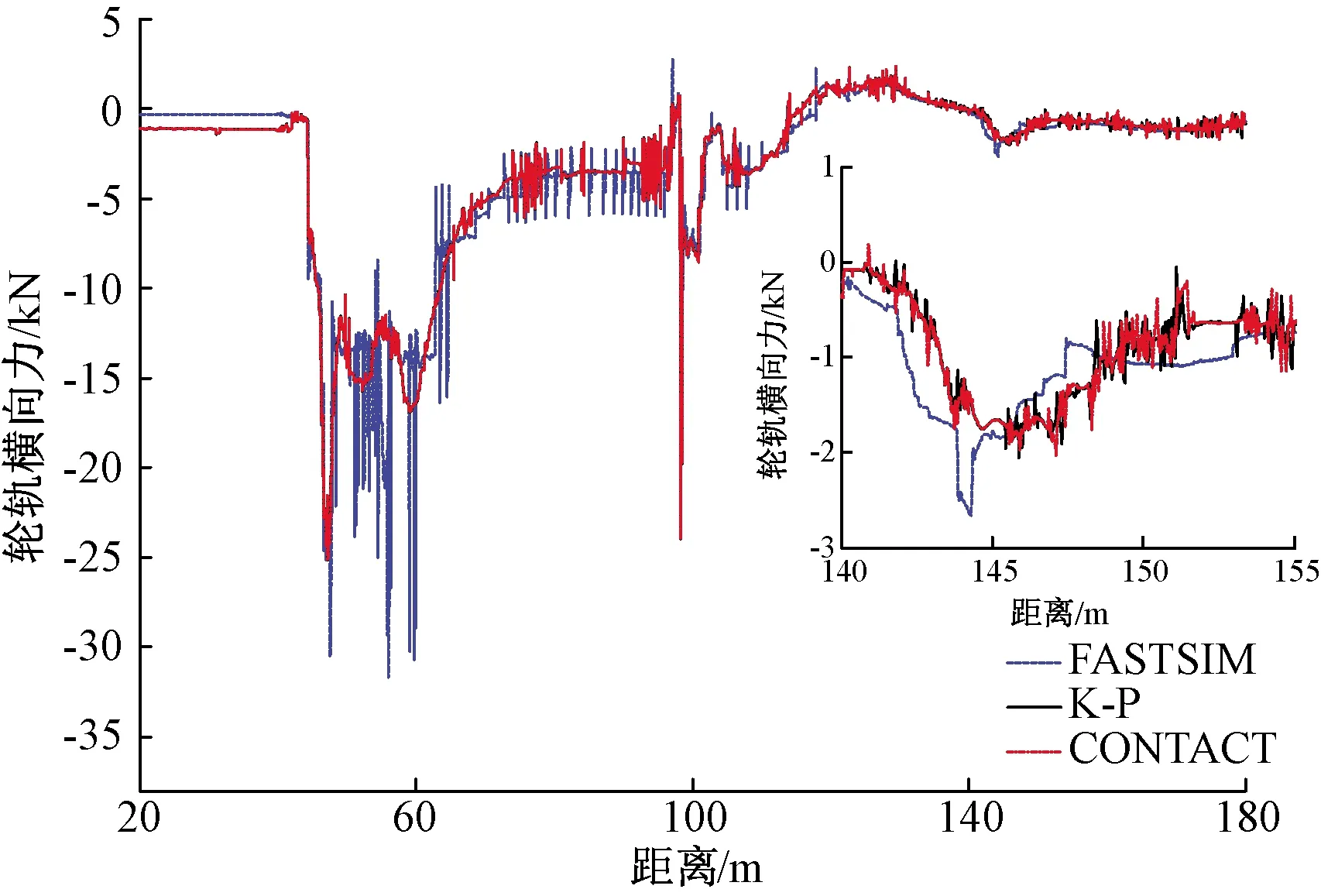
圖11 不同輪軌接觸理論下輪軌橫向力計算結果對比

圖12 不同輪軌接觸理論下輪軌垂向力計算結果對比

表4 不同輪軌滾動接觸計算方法結果比較

3 車輛通過道岔的振動特性分析

為研究車輛通過道岔的振動特性，根據建立的車輛-道岔耦合動力模型，設置60～100 km/h，步長為10 km/h的5個速度等級，以及車輛在不同運行里程下的磨耗型面。應用車輛振動特性分析指標分析磨耗型面對過岔時的振動特性影響。

圖13 輪軌力峰值變化情況

3.1 輪岔相互作用

圖13(a)為不同速度和磨耗里程型面輪軌橫向力的極大值變化情況，輪軌橫向力達到最大值時的情況為：車輪通過道岔轉轍區；車輪通過尖軌位置。輪軌橫向力最大值與速度成正比，且速度提高對輪軌橫向力的增長呈現非線性趨勢。但是當型面磨耗增大到一定程度時，其輪軌橫向力最大值反而會減小。出現這種情況的原因在于當磨耗增大到一定程度時，車輪經過道岔時接觸形式會變成多點、共形接觸，這種接觸形式會改善橫向的輪軌匹配特性[12]。例如，車輛在采用無損型面與已運行25萬km的型面進行分析時，同樣以80 km/h通過岔道，輪對橫向力最大值分別為27.43 kN和22.39 kN，下降幅度可達18.37%。圖13(b)為輪軌垂向力最大值的變化情況，輪軌垂向力最大值與磨耗深度成正比，磨耗深度越大，輪軌垂向力最大值越大。根據高速列車動力學規范，輪軌垂向力極限值Pmax=170 kN。當磨耗為0.5 mm，車輛以100 km/h的過岔速度運行時，輪軌垂向力峰值為176.87 kN，超出運行允許極限值。

以80 km/h過岔速度分析，圖14為輪軌力功率譜密度變化的對數圖，在12 Hz后顯露出差異，其中15.3萬km的功率譜數值最大，說明該里程的磨耗型面產生的輪軌橫向力作用最劇烈。輪軌垂向力功率譜密度變化曲線表明，輪軌垂向力頻率分布主要為10 Hz以下的低頻。對比初始型面的曲線和各磨耗階段的功率譜曲線不難發現，在大于100 Hz的中高頻，隨著車輪型面磨耗量增加，功率譜密度值隨著運營里程數增大而明顯上升。

圖14 輪軌力功率譜密度變化情況

3.2 車輛運行安全平穩性

3.2.1 安全性

圖15～圖17對車輛的脫軌系數、輪重減載率和磨耗功率的峰值變化進行了說明。其中輪軌橫向力最大值通常在轍叉區產生，這與脫軌系數表現出的規律大致相同。磨耗量逐漸增加時，脫軌系數整體波動較小。當車輛使用未產生磨耗的車輪以100 km/h的速度通過道岔時，脫軌系數達到最大值0.51。輪重減載率由于作用時間極短(小于0.01 s)，會經常出現超過標準的情況[6]，因此需要對其進行濾波處理。經過20 Hz的低通濾波處理，輪重減載率變化情況如圖16所示，車輪型面磨耗量增加后，5條曲線均表現出了減小的趨勢，且車輛運行速度越大，減小趨勢就越明顯。

圖15 脫軌系數峰值變化情況

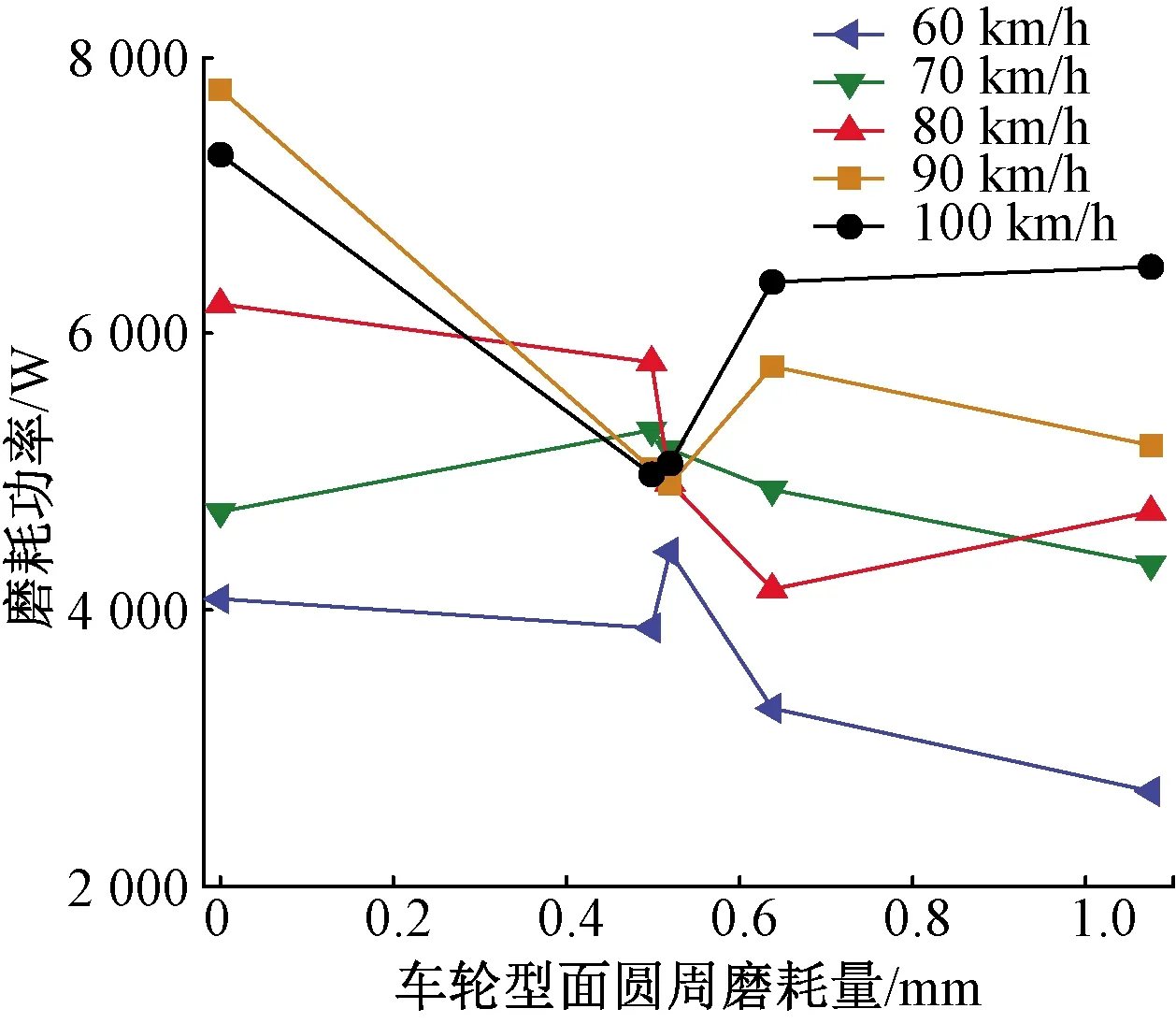
圖17 磨耗功率峰值變化情況

利用磨耗功率評價車輪的磨耗性能。

Mwear=|Fx·ξx|+|Fy·ξy|+|Mn·wn|

( 9 )

式中：F為蠕滑力，下標x表示方向為縱向，即縱向蠕滑力；ξ為蠕滑率，下標y表示方向為橫向，即橫向蠕滑率；Mn為自旋蠕滑力矩；wn為自旋蠕滑率。

從磨耗功率峰值變化情況可知，在磨耗進入一定階段后(磨耗量0.5 mm左右)，無論哪個速度等級，輪軌磨耗功率會達到約5 kW的一個相對穩定的數值，其后峰值會隨著速度等級不同繼續增大或者減小[12]。

3.2.2 平穩性

(1)車體振動特性

圖18、圖19為車輛以80 km/h標準過岔速度通過時的車體橫向和垂向加速度功率譜密度對數變化圖。從圖中可以看出，隨著運營里程數增加，車體橫向加速度功率譜密度曲線波動情況并不明顯。車體橫向振動加速度主頻為1.4 Hz，垂向振動加速度主頻為0.8 Hz。垂向加速度功率譜曲線整體幅值上升。由于道岔結構不平順主要表現為短波，主要引起輪軌間的高頻沖擊力，而車體加速度主要受長波軌道不平順的影響較大，因此對車體垂橫向加速度的影響較小。

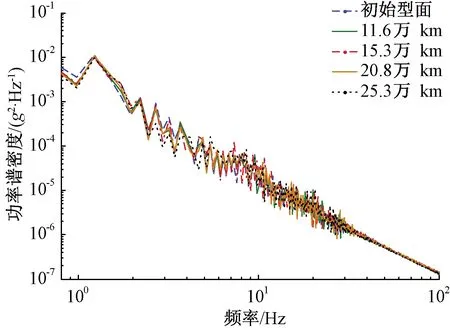
圖18 車體橫向加速度功率譜變化情況

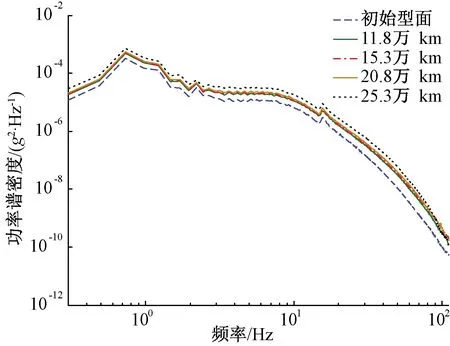
圖19 車體垂向加速度功率譜變化情況

Sperling指標通常作為衡量車輛乘坐舒適性和運行品質的指標。Sperling指標變化情況如圖20、圖21所示，其中橫向Sperling指標隨著磨耗量增加無明顯變動，最大值為100 km/h過岔速度時，達到2.16。說明橫向Sperling指標主要對速度變化敏感。垂向Sperling指標隨著磨耗量累積逐漸上升。說明車輪型面的磨耗會影響列車乘坐舒適性，尤其對垂直方向舒適度影響明顯。車輪初始型面在80 km/h過岔速度條件下，垂向Sperling指標為1.07，運行25.3萬km后，指標的最大值達到1.15。橫垂向的Sperling指標在5種速度等級下均小于安全限度值2.5，表明車輪磨耗對乘坐舒適度的影響在可接受規范內。

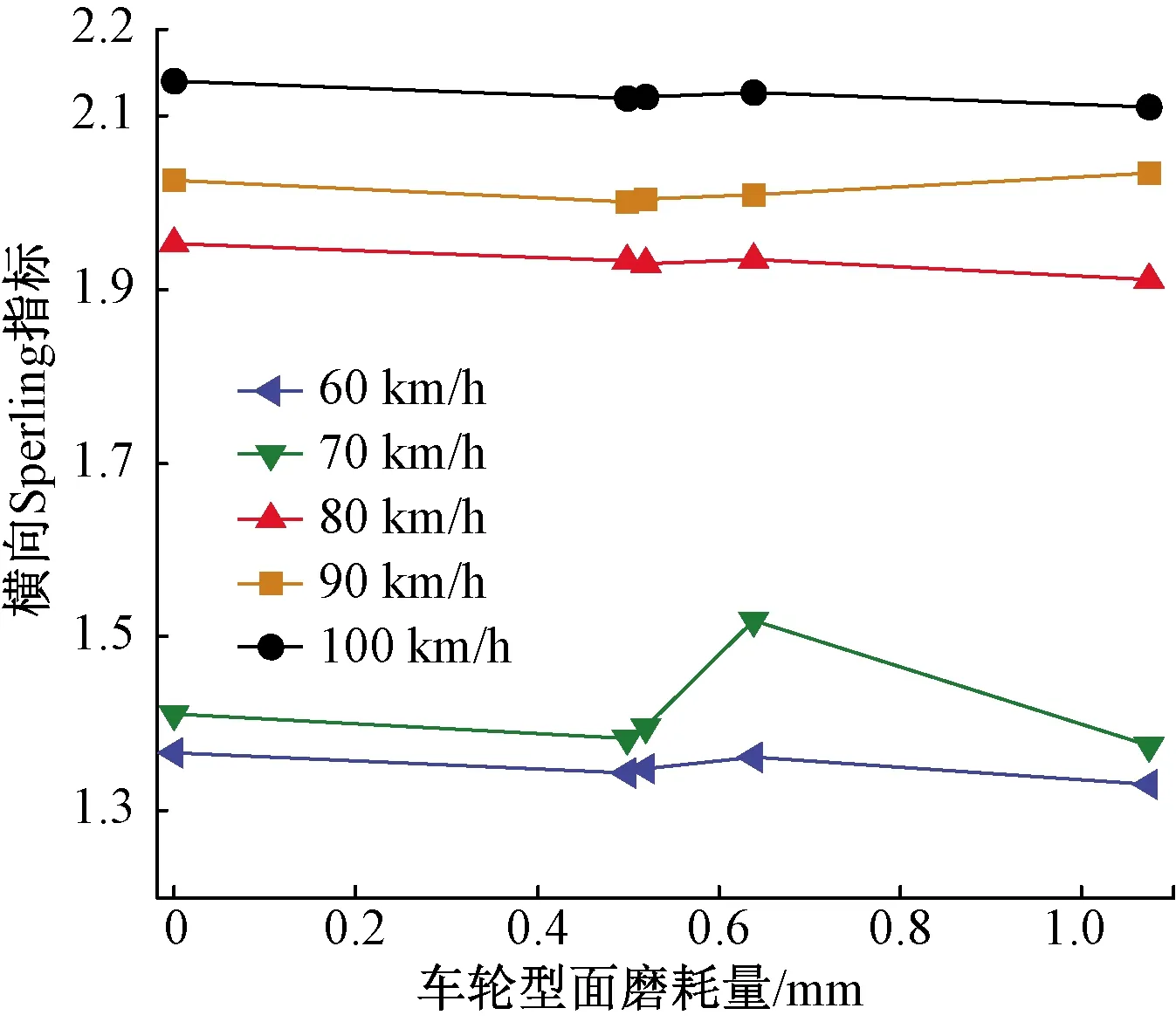
圖20 車體橫向Sperling指標變化情況

圖21 車體垂向Sperling指標變化情況

(2)構架振動特性

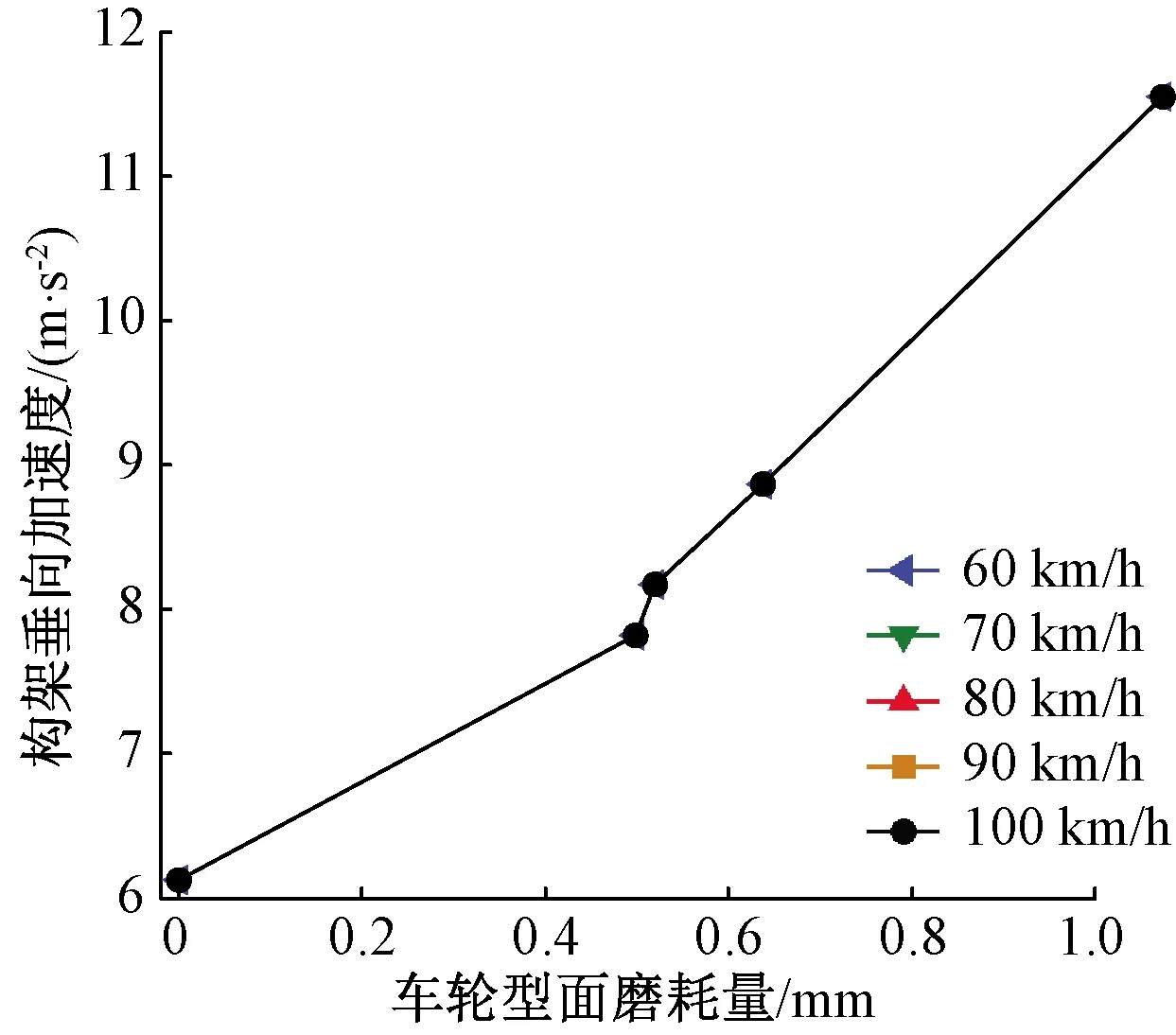
圖22 構架垂向振動加速度峰值變化情況

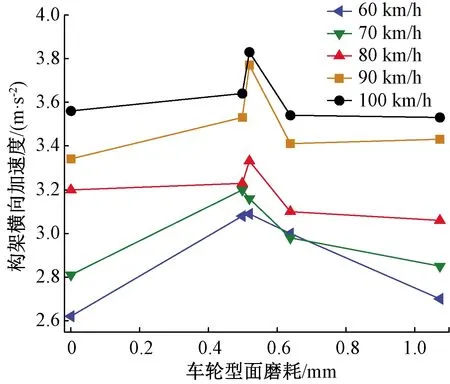
圖23 構架橫向振動加速度峰值變化情況

圖22、圖23分別是車輛構架垂向和橫向振動加速度峰值變化圖，從圖中可以看出，構架的垂向加速度峰值基本不隨速度變化而波動，5種速度下的峰值曲線基本重合。車輪凹形磨耗對構架垂向振動加速度峰值影響較為突出，隨著磨耗的惡化，加速度峰值出現明顯增長，從初始型面的6.15 m/s2增大到11.6 m/s2，提高了88.61%。構架橫向振動加速度峰值先小幅度上升，再下降回歸，運營25.3萬km下的橫向振動加速度值和初始無磨耗型面振動數值相似。構架橫向振動加速度峰值最大可達3.83 m/s2。

(3)輪對振動特性

圖24、圖25為輪對加速度峰值變化圖。輪對垂向振動加速度和構架垂向加速度變化規律相似，在車輪磨耗量小于0.5 mm的階段，輪對的垂向最大加速度值保持穩定，基本沒有變化。但是當磨耗量超過0.5 mm后，輪對的垂向最大加速度值變化幅度較大，加速度最大值由64 m/s2增大到102 m/s2。當車輪磨耗量從0增加到0.5 mm時，橫向振動加速度最大值會逐漸減小，車輪磨耗量為0.5～0.6 mm時，橫向振動加速度最大值會有小幅度變化。總體看來，輪對橫向振動加速度峰值會隨著磨耗量增加略有降低。

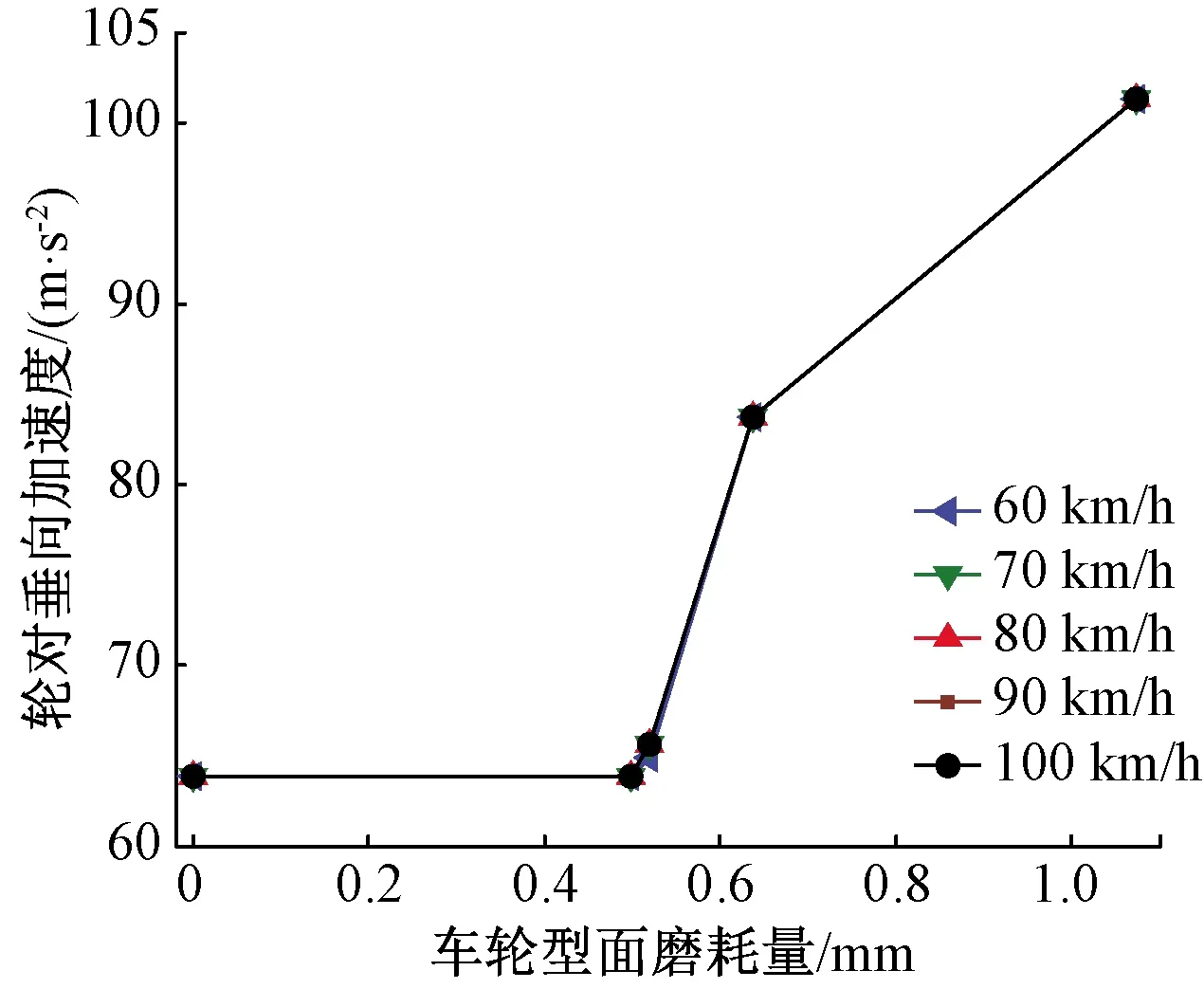
圖24 輪對垂向最大振動加速度變化情況

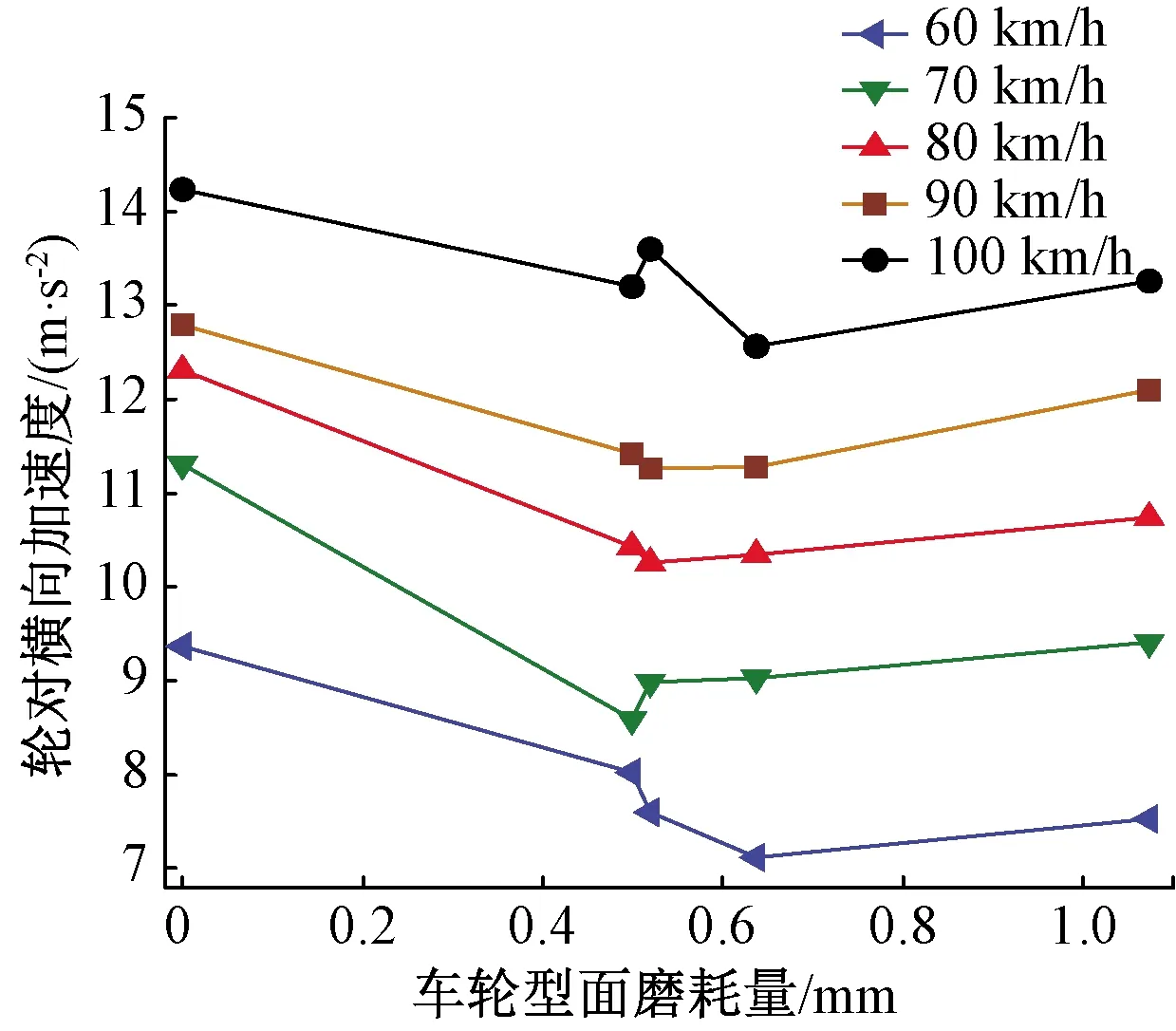
圖25 輪對橫向最大振動加速度變化情況

3.3 道岔振動特性分析

圖26、圖27所示為鋼軌振動位移峰值變化情況，車輪型面磨耗量相同的情況下，列車通過道岔速度越大，鋼軌的橫、垂向振動位移峰值越大；在列車通過道岔速度相同的情況下，車輪型面磨耗量增大的過程中，橫向振動位移峰值逐漸減小但垂向振動位移峰值有先減小后增大的趨勢。

圖26 鋼軌垂向振動位移峰值變化情況

圖27 鋼軌橫向振動位移峰值變化情況

4 結論

(1)車輪型面磨耗量與輪軌垂向力大小成正比，與輪軌橫向力成反比。

(2)磨耗功率在列車不同運營里程內變化，會統一達到一個相對穩定數值5 kW左右。車體振動加速度、Sperling指標、構架和輪對振動加速度，均在垂向方向對車輪型面磨耗較敏感，但橫向方向變化相對較小。

(3)道岔區域鋼軌的各方向振動位移峰值與車輪型面磨耗的關系差異較大，其中橫向聯系較為緊密，垂向影響較小。

(4)對道岔尖軌、心軌等關鍵部位進行設計時，需重點考慮不同運營里程下的車輪磨耗型面帶來的影響，以提升列車運行品質。