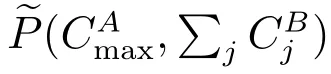同時最優化時間表長與總完工時間的雙代理單機序列分批排序問題

何 程, 韓鑫鑫

(河南工業大學理學院，鄭州 450001)

1 Introduction

The multi-agent scheduling problem was introduced by Agnetis et al[1]and Baker and Smith[2]. There are several agents, each agent has a job set. The agents have to schedule their jobs on a common processing resource, i.e., a single machine, and each agent wishes to minimize an objective function that depends on the completion times of his own set of jobs. The problem is to find a schedule that satisfies each agent’s requirements for his own objective function.

Scheduling problems involving multiple agents arise naturally in many applications in which negotiation procedures are needed. For example, in industrial management,the multi-agent scheduling problem is formulated as a sequencing game, where the objective is to devise some mechanisms to encourage the agents to cooperate with a view to minimize the overall cost (Curiel et al[3]and Hamers et al[4]).

By now, the multi-agent scheduling problem has been extensively investigated.Agnetis et al[5]studied single-machine scheduling problems with multiple agents, and the considered objective functions are the maximum of regular functions, the number of tardy jobs, and the total weighted completion time. Cheng et al[6,7]and Yuan[8]also the studied the multi-agent scheduling on a single machine.

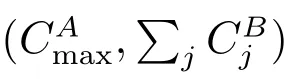
2 Preliminaries

1) pXjis the processing time of job JXj(X ∈{A,B}, j =1,2,··· ,nX).

2) CXj(σ) is the completion time of job JXjin σ(X ∈{A,B}, j =1,2,··· ,nX).

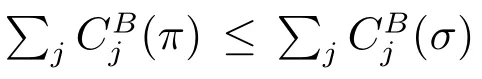
3 Pareto optimal algorithm

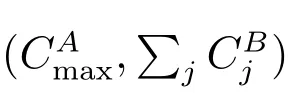
Without loss of generality, we may regard the batches of agent A as a single big batch BAwith the processing time

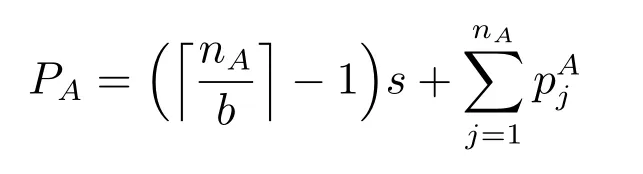
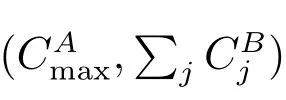
Lemma 2For each Pareto optimal point of problem,there exists a corresponding effective Pareto optimal schedule.

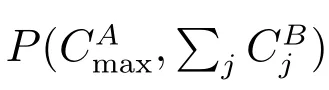
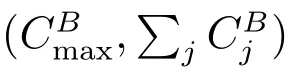
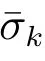
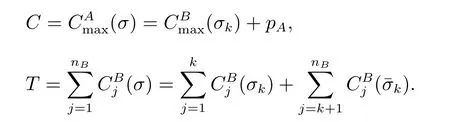
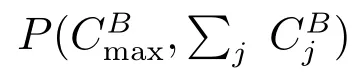
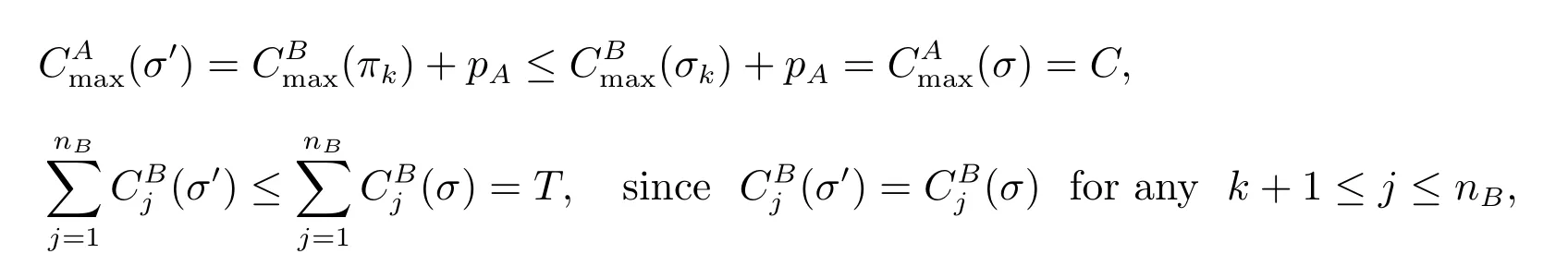
and at least one of the inequalities is strict, which contradicts to the Pareto optimality of σ. So (i) follows.

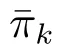
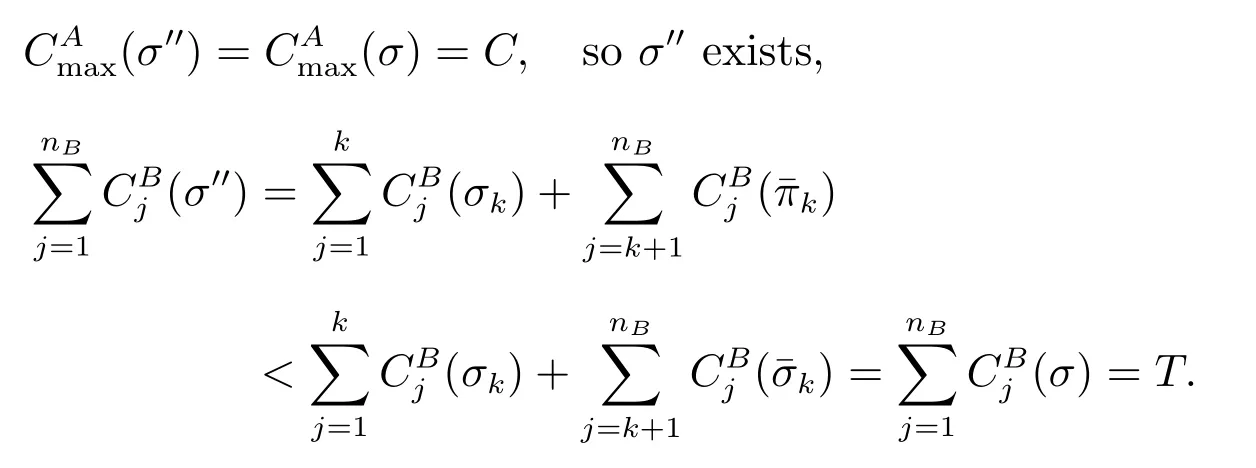
This contradicts to the Pareto optimality of σ. So (ii) follows.

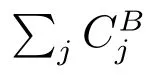
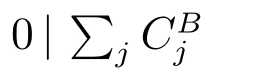
Let Fl(j) be the minimum total completion time of jobs {JB1,JB2,··· ,JBj} with l batches and the starting time be zero. The recursion equation for l ≤j ≤lb is:

with initial conditions

F0(0)=0 and F0(j)=+∞, for j >0,

Fl(j)=+∞, for j lb,

where αlj=max{l ?1,j ?b}, βlj=min{j ?1,(l ?1)b}.

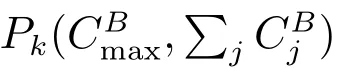
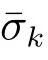
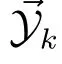
Then we define

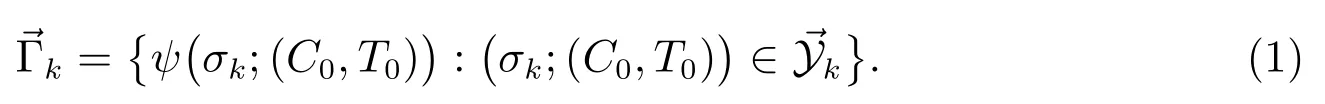
Finally, we define

Thus, we have the following conclusion by Lemma 3.

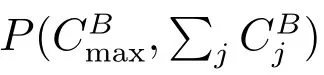
Algorithm POP Step 0Calculate

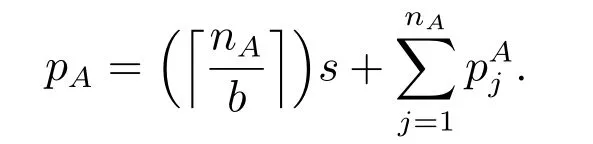
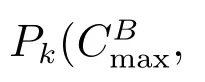
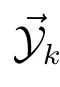
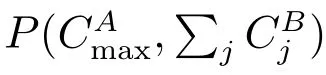
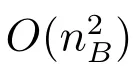
4 Unbounded model

Similar to Lemma 1, we may get the following lemma.

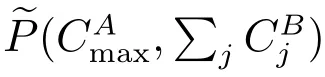
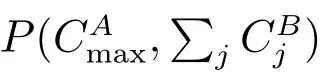
with the initial conditions

F0(0)=0 and F0(j)=+∞, for j >0,

Fl(j)=+∞, for j