基于修理設備可更換和修理延遲策略的兩不同型部件冷貯備可修系統
魏瑛源, 唐應輝
(1- 河西學院數學與統計學院,甘肅張掖 734000; 2- 四川師范大學數學科學學院,成都 610068)
1 引言
冷貯備可修系統的研究中,已有文獻通常都假定修理設備是完全可靠的.事實上,由于磨損和老化等情況,在修理故障部件的過程中,修理設備也可能會發生失效,此時需要被更換后再繼續工作.另外,部件發生故障后,要先判斷故障原因,或者修理工不在崗(休假或去做輔助性工作),使得故障部件不可能立即得到修理.基于這樣的實際情況,文獻[1–12]把“修理有延遲”或“修理設備可發生失效且可更換”的策略引入到可修系統的研究中,這是一類更一般的可修系統,既有實際應用背景,又有理論分析意義.
文獻[13]在假定部件的工作壽命、故障部件的修理時間和修理延遲時間都具有概率密度函數的條件下(這個假定條件較苛刻),研究了修理有延遲的兩個不同型部件組成的冷貯備可修系統,得到了系統首次故障前時間和系統的可用度等可靠性指標.文獻[14]研究了修理設備可更換的兩個不同型部件組成的冷貯備可修系統,得到了系統和修理設備的一些可靠性指標.正是在這些文獻研究的綜合啟發下,本文討論修理設備可更換且修理有延遲的冷貯備可修系統,其中故障部件的修理時間和修理延遲時間、修理設備失效后的更換時間都服從任意分布(不一定是連續型),擺脫了對一般連續型分布的依賴性,從模型方面極大地推廣了已有文獻的研究,使得研究的系統更具一般性,其分析也更復雜.我們使用Markov 更新過程理論、全概率分解技術、L 變換和LS 變換,給出了系統和修理設備的可靠性指標的表達式.系統的描述如下:
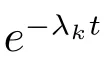
1) 在系統正常工作期間,修理設備處于冷關閉狀態,不發生失效;
2) 工作部件發生故障時,貯備部件立即去替換而轉為工作狀態,轉換開關是完全可靠的,狀態轉換是瞬時完成的;
3) 當一個部件故障時,若修理設備處于關閉狀態,則該部件的修理有延遲;在先故障部件的修理延遲時間內或修理時間內故障的部件,其修理沒有延遲,但是需要等待先故障部件修復好后再接受修理;
4) 當修理設備失效時,正在接受修理的部件需等待其更換后再繼續接受修理,修理設備更換后立即轉為工作狀態,部件已修理過的時間依然有效;
5) 當部件被修復好后,若此時系統中無待修部件,則修理設備自行關閉,否則,接著修理待修部件;
6) 修復好的部件,或進入冷貯備狀態(若此時另一個部件正在工作),或立即進入工作狀態(若此時另一個部件已故障);
7) 故障部件被修復好后,完全恢復其功能;
8) Xk, Yk, Wk, U, V, k =1,2 相互獨立.
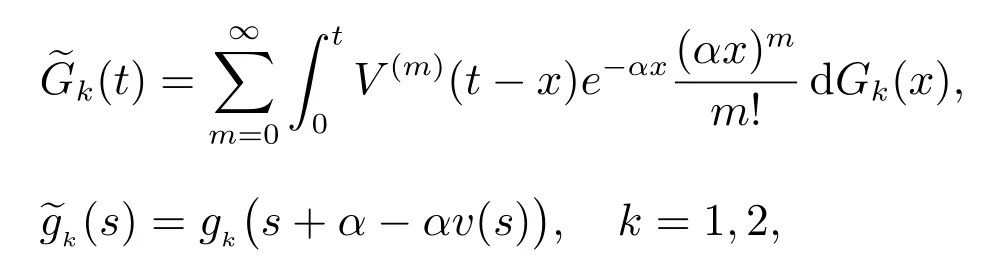
其中
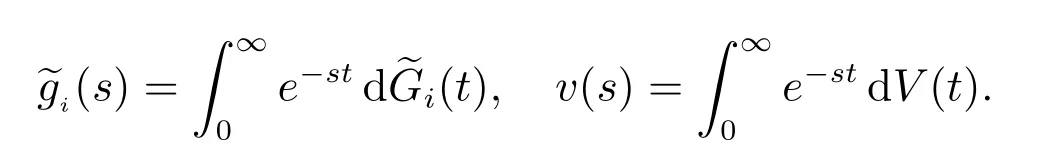
注1本文一律用g(s)和g?(s)分別表示G(t)的Laplace-Stieltjes 變換(簡稱LS 變換)和Laplace 變換(簡稱L 變換),即
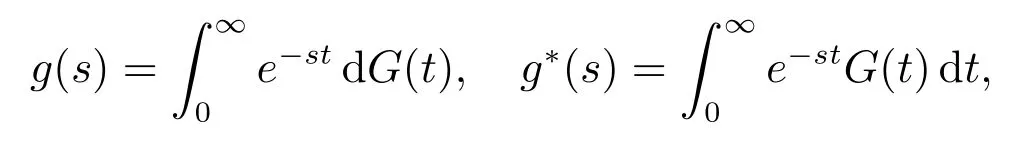
G(k)(t)表示G(t)的k 重卷積,且G(0)(t)=1, t ≥0;Z0表示t=0 時系統的狀態;?(s)表示復變數s 的實部.
2 更新過程
系統的狀態定義為:狀態0(1)表示部件1(2)正在工作,部件2(1)開始冷貯備;狀態2(3)表示部件2(1)正在工作,部件1(2)開始修理延遲;狀態4(5)表示部件2(1)正在工作,部件1(2)開始被修理;狀態6(7)表示部件2(1)正在待修,部件1(2)開始被修理.
用Z(t) = j 表示系統在時刻t 處于狀態j, j = 0,1,··· ,7.由負指數分布的無記憶性可知,進入狀態0,1,··· ,7 的時刻都是系統的再生點.用Tn表示系統第n 次發生狀態轉移的時刻,T0= 0;令Zn= Z(Tn+0)表示系統在第n 次狀態轉移時所進入的狀態.容易驗證,{Zn, Tn; n=0,1,···}是一個狀態空間為E ={0,1,··· ,7}的齊次Markov 更新過程,{Z(t), t ≥0}是一個齊次半Markov 過程.由半Markov 核的定義
Qij(t)=P{Zn+1=j, Tn+1?Tn≤t|Zn=i}, i,j =0,1,··· ,7, n=0,1,··· ,
可以計算出所有半Markov 核為
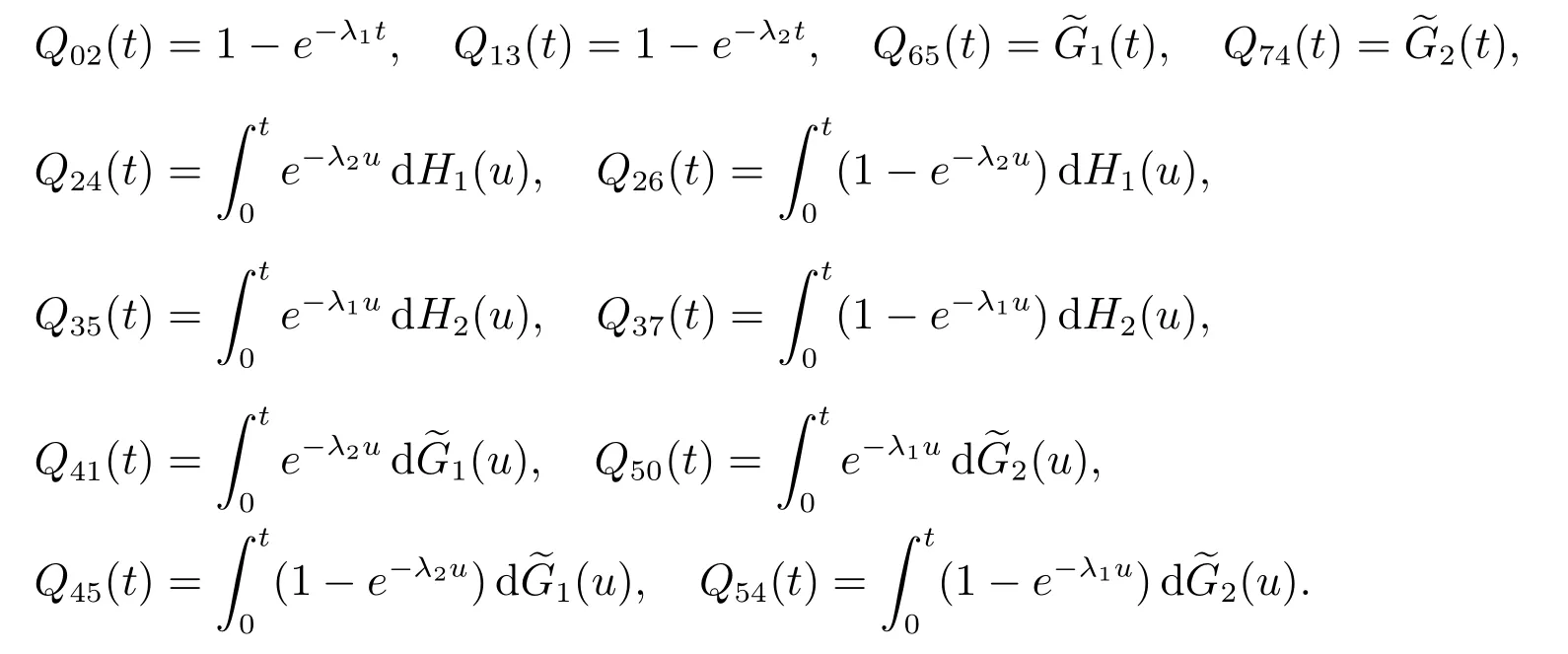
為下面討論問題方便,引進四個虛設狀態:
狀態8(9):部件1(2)正處于修理延遲,部件2(1)開始待修;
狀態10(11):部件1(2)正在被修理,部件2(1)開始待修.
由于故障部件的修理延遲時間和修理時間均服從任意分布,因而進入狀態8, 9, 10, 11的時刻不是系統的再生點.顯然狀態6,7,··· ,11 都是系統的故障狀態,且
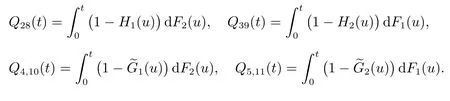
對以上各式作LS 變換,并記
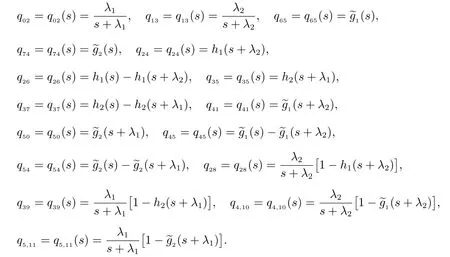
另外,記
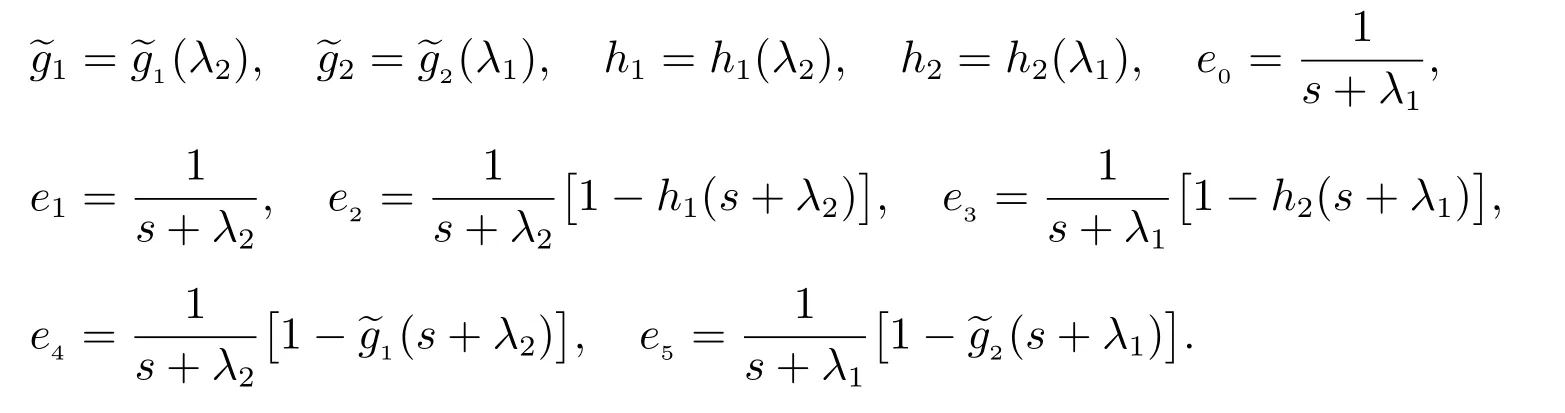
3 系統的可靠性指標
3.1 系統首次故障前時間的分布
令
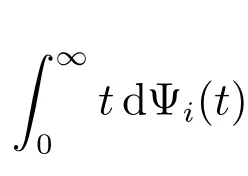
如果一個可修系統一旦發生故障將產生災難性后果,那么系統首次故障前時間的分布及其均值是該系統最重要的可靠性數量指標.另外,根據Ψi(t),能得到系統在時刻t 以前都正常的概率為1 ?Ψi(t) = P{δ > t|Z0= i},這也是可修系統在時間區間(0,t]內不故障的概率.
定理1對?(s)>0,Ψi(t)的LS 變換為
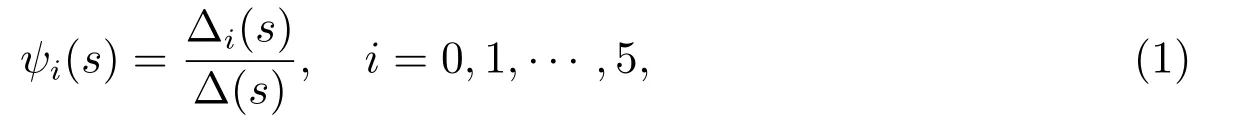
其中
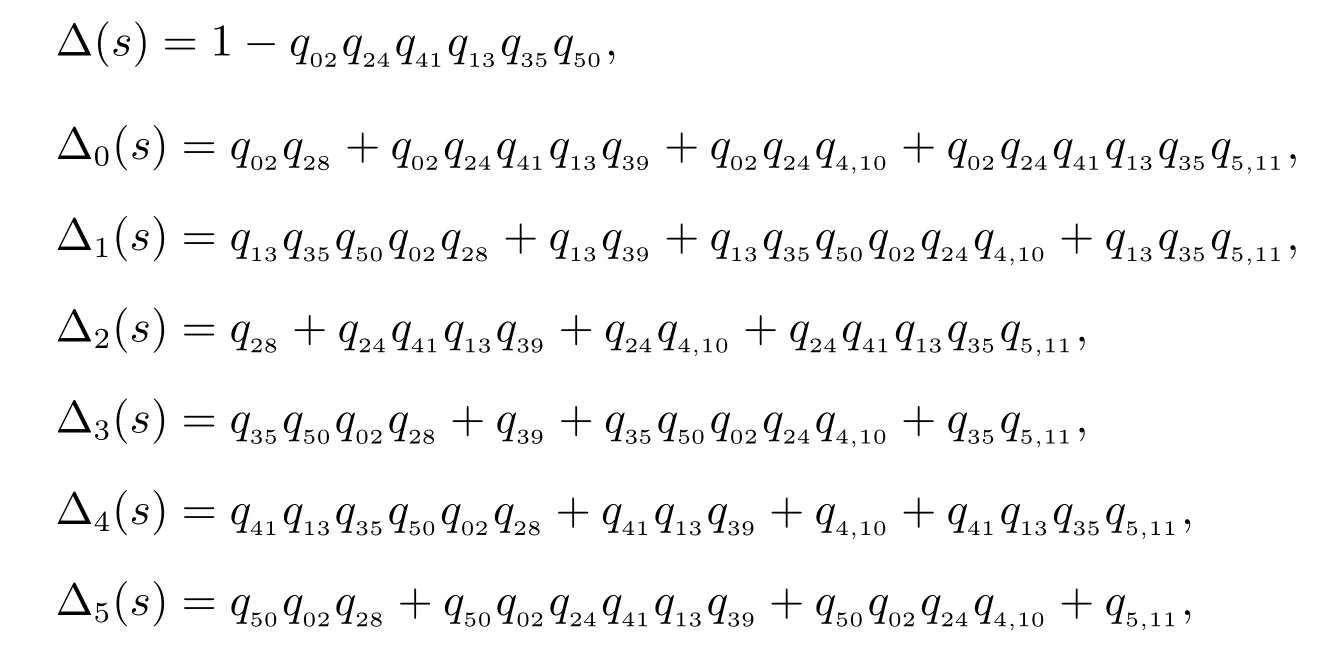
且系統首次故障前的平均時間為
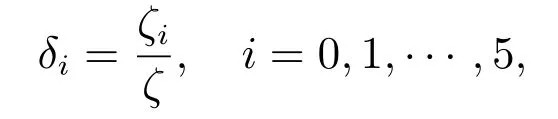
其中
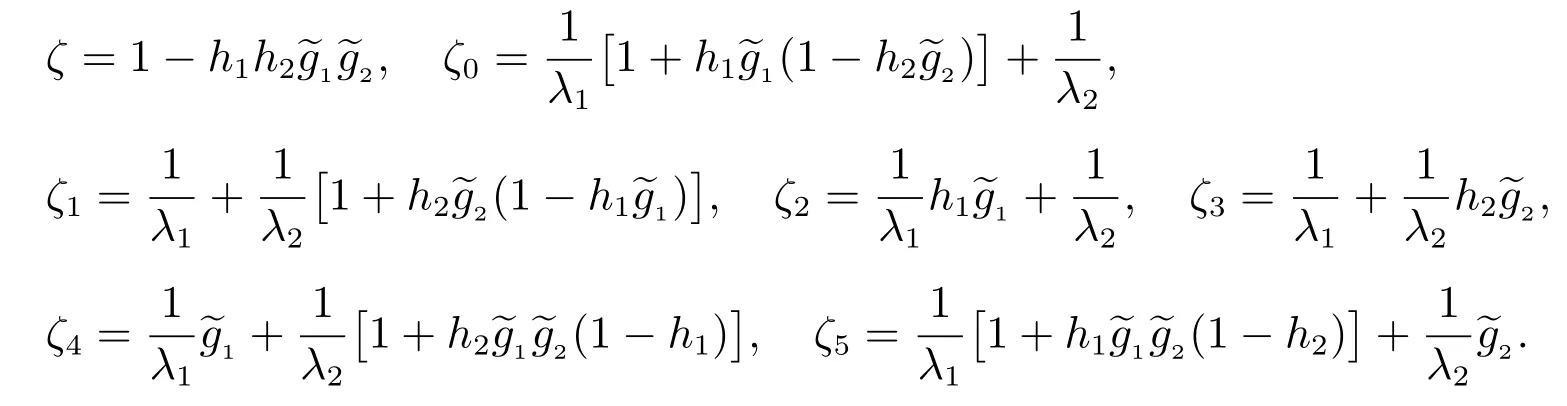
證明 由Ψ2(t)的定義及系統狀態的轉移關系,得
Ψ2(t)=P{δ ≤t,T1≤t|Z0=2}+P{δ ≤t,T1>t|Z0=2}
=Q24(t)?Ψ4(t)+Q28(t).
類似地,可得
Ψ0(t)=Q02(t)?Ψ2(t), Ψ1(t)=Q13(t)?Ψ3(t), Ψ3(t)=Q35(t)?Ψ5(t)+Q39(t),
Ψ4(t)=Q41(t)?Ψ1(t)+Q4,10(t), Ψ5(t)=Q50(t)?Ψ0(t)+Q5,11(t).
對各式兩端作LS 變換,可得(1)式.再由
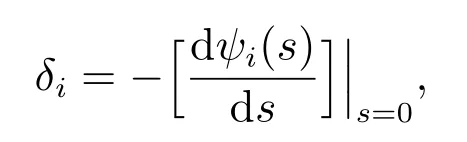
可得系統首次故障前平均時間.
3.2 系統的可用度
對t ≥0,令

定理2對?(s)>0,Ai(t)的L 變換為

其中
η(s)=(1 ?q41q13q37q74)(1 ?q50q02q26q65)?(q41q13q35+q45)(q50q02q24+q54),
η0(s)=q02η2(s)+e0η(s), η1(s)=q13η3(s)+e1η(s),
η2(s)=(q24+q26q65q54)(e1+q41q13e3)+(q41q13q35+q45)(q24e0?q54e2)+(1 ?q41q13q37q74)(q26q65e0+e2),
η3(s)=(q35+q37q74q45)(e0+q50q02e2)+(q50q02q24+q54)(q35e1?q45e3)+(1 ?q50q02q26q65)(q37q74e1+e3),
η4(s)=(q41q13q35+q45)(e0+q50q02e2)+(1 ?q50q02q26q65)(e1+q41q13e3),
η5(s)=(1 ?q41q13q37q74)(e0+q50q02e2)+(q50q02q24+q54)(e1+q41q13e3),
η6(s)=q65η5(s), η7(s)=q74η4(s),
且系統的穩態可用度為

與初始狀態i 無關,i ∈E,其中
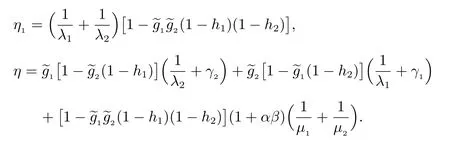

證明 令則由Ai(t)的定義及系統狀態的轉移關系,得
A2(t)=P{X(t)=1,T1≤t|Z0=2}+P{X(t)=1,T1>t|Z0=2}
=Q24(t)?A4(t)+Q26(t)?A6(t)+1 ?Q24(t)?Q26(t).
類似地,可得
A0(t)=Q02(t)?A2(t)+1 ?Q02(t), A1(t)=Q13(t)?A3(t)+1 ?Q13(t),
A3(t)=Q35(t)?A5(t)+Q37(t)?A7(t)+1 ?Q35(t)?Q39(t),
A4(t)=Q41(t)?A1(t)+Q45(t)?A5(t)+1 ?Q41(t)?Q4,10(t),
A5(t)=Q50(t)?A0(t)+Q54(t)?A4(t)+1 ?Q50(t)?Q5,11(t),
A6(t)=Q65(t)?A5(t), A7(t)=Q74(t)?A4(t).
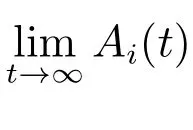
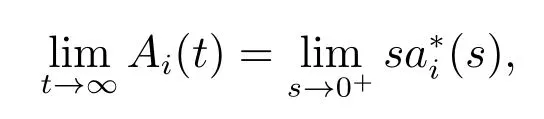
于是再使用L’Hospital 法則,可得(3)式.
3.3 系統在有限區間(0,t]內發生故障的平均次數
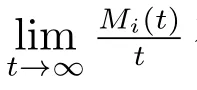
定理3對?(s)>0,Mi(t)的LS 變換為

其中
ρ0(s)=q02ρ2(s), ρ1(s)=q13ρ3(s), ρ6(s)=q65ρ5(s), ρ7(s)=q74ρ4(s),
ρ2(s)=(q41q13q35+q45)(q24q5,11?q28q54)+(q41q13q39+q4,10)(q24+q26q65q54)+(1 ?q41q13q37q74)(q26q65q5,11+q28),
ρ3(s)=(q50q02q24+q54)(q35q4,10?q39q45)+(q50q02q28+q5,11)(q35+q37q74q45)+(1 ?q50q02q26q65)(q37q74q4,10+q39),
ρ4(s)=(q41q13q35+q45)(q50q02q28+q5,11)+(1 ?q50q02q26q65)(q41q13q39+q4,10),ρ5(s)=(q50q02q24+q54)(q41q13q39+q4,10)+(1 ?q41q13q37q74)(q50q02q28+q5,11),
且系統的穩態故障頻度為

與初始狀態i 無關,i ∈E,其中η 由定理2 給出,
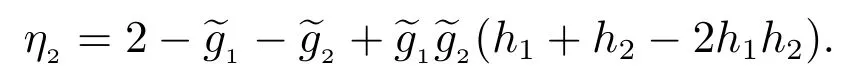
證明 類似于定理2 的證明.
3.4 系統在時刻t 等待修理的概率
系統在時刻t 等待修理是指在時刻t 兩部件都故障,且都沒有被修理.因此,考察時刻0 系統由狀態i 出發,在時刻t 等待修理的概率,可進一步明確系統的不可用度.對t ≥0,令
Di(t)=P{系統在時刻t 等待修理|Z0=i}, i ∈E.
定理4對?(s)>0,Di(t)的L 變換為

其中
ξ0(s)=q02ξ2(s), ξ1(s)=q13ξ3(s), ξ6(s)=q65ξ5(s), ξ7(s)=q74ξ4(s),
ξ2(s)=(q24+q26q65q54)q41q13(q39?q37)+(q28q26)(1 ?q41q13q37q74?q41q13q35q54?q45q54),
ξ3(s)=(q35+q37q74q45)q50q02(q28?q26)+(q39q37)(1 ?q50q02q26q65?q50q02q24q45?q54q45),
ξ4(s)=(q41q13q35+q45)q50q02(q28?q26)+(1 ?q50q02q26q65)q41q13(q39?q37),
ξ5(s)=(q50q02q24+q54)q41q13(q39?q37)+(1 ?q41q13q37q74)q50q02(q28?q26),
且穩態概率為

與初始狀態i 無關,i ∈E,其中η 由定理2 給出,
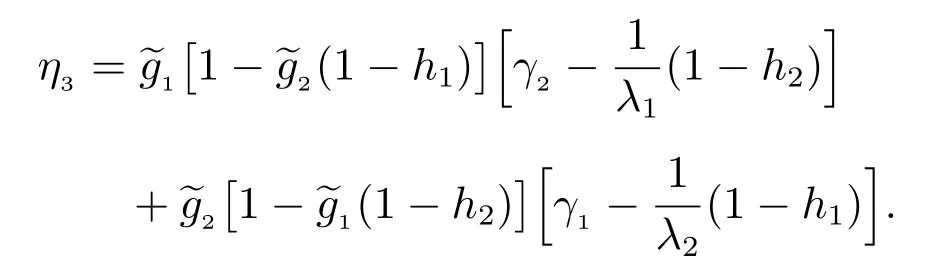
證明 類似于定理2 的證明.
3.5 修理延遲時間對δ0, A0 的影響分析
討論修理延遲時間的改變對系統首次故障前平均時間和系統的穩態可用度的影響程度.假設:
(i) 部件1 和部件2 是兩個同型部件,壽命服從參數為λ 的負指數分布;
(ii) α=0,即修理設備完全可靠,不發生失效;
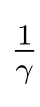
(iv) 部件故障后的修理時間服從參數為μ的負指數分布;
(v) Z0=0,即時刻0 系統從狀態0(部件1 在工作,部件2 開始冷貯備)開始.
用δ0和A0分別表示系統首次故障前平均時間和系統的穩態可用度.
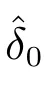
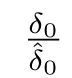
表1: μ和γ(γ =)的不同值所對應的δAd 的值
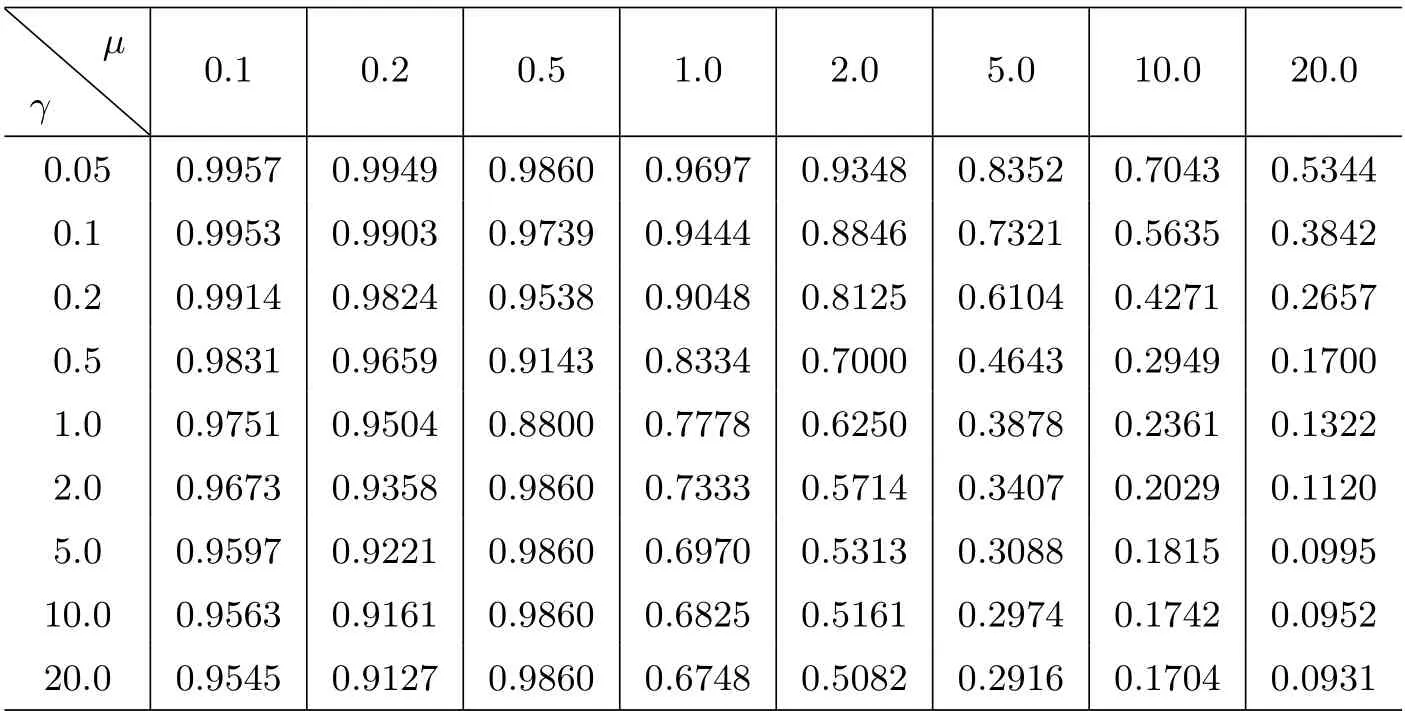
表1: μ和γ(γ =)的不同值所對應的δAd 的值
μγ 0.1 0.2 0.5 1.0 2.0 5.0 10.0 20.0 0.05 0.5344 0.1 0.9957 0.9949 0.9860 0.9697 0.9348 0.8352 0.7043 0.3842 0.2 0.9953 0.9903 0.9739 0.9444 0.8846 0.7321 0.5635 0.2657 0.5 0.9914 0.9824 0.9538 0.9048 0.8125 0.6104 0.4271 0.1700 1.0 0.9831 0.9659 0.9143 0.8334 0.7000 0.4643 0.2949 0.1322 2.0 0.9751 0.9504 0.8800 0.7778 0.6250 0.3878 0.2361 0.1120 5.0 0.9673 0.9358 0.9860 0.7333 0.5714 0.3407 0.2029 0.0995 10.0 0.9597 0.9221 0.9860 0.6970 0.5313 0.3088 0.1815 0.0952 20.0 0.9563 0.9161 0.9860 0.6825 0.5161 0.2974 0.1742 0.9545 0.9127 0.9860 0.6748 0.5082 0.2916 0.1704 0.0931
表2: μ和γ(γ =)的不同值所對應的AAd 的值
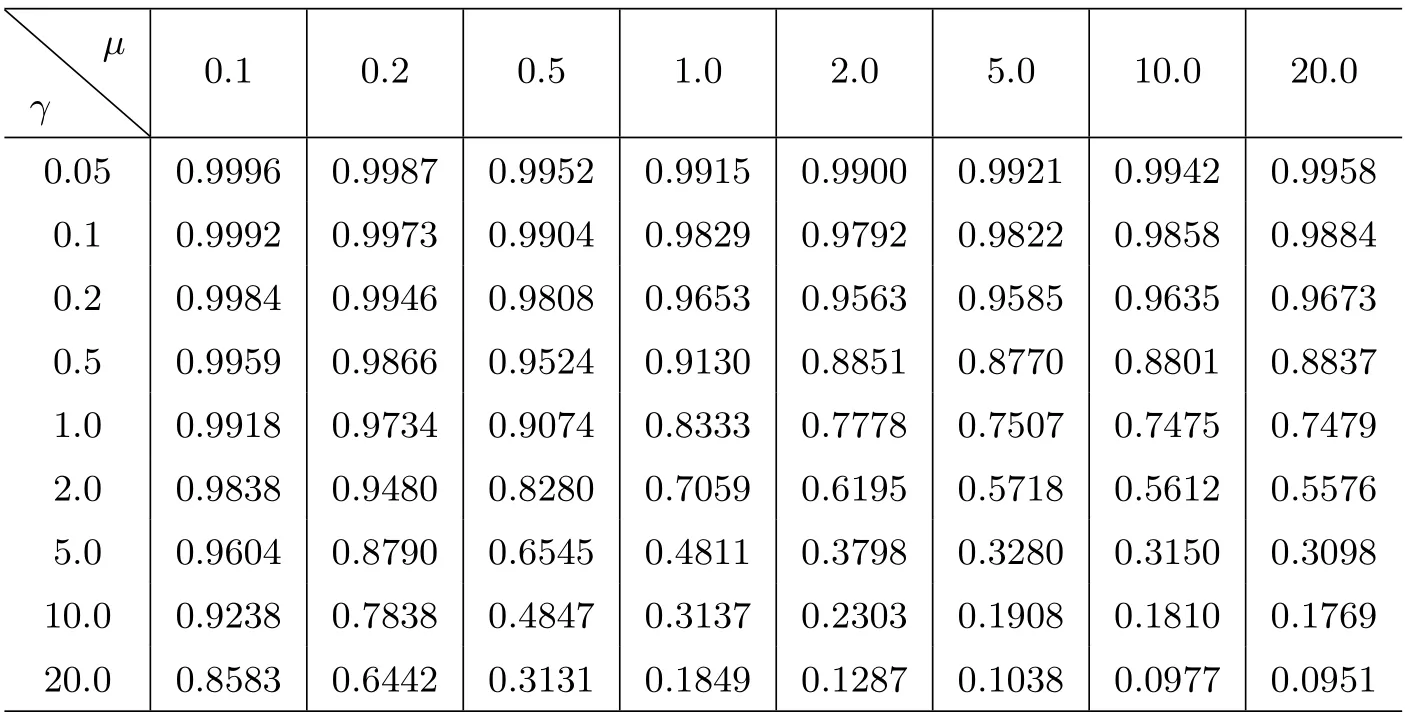
表2: μ和γ(γ =)的不同值所對應的AAd 的值
μγ 0.1 0.2 0.5 1.0 2.0 5.0 10.0 20.0 0.05 0.9958 0.1 0.9996 0.9987 0.9952 0.9915 0.9900 0.9921 0.9942 0.9884 0.2 0.9992 0.9973 0.9904 0.9829 0.9792 0.9822 0.9858 0.9673 0.5 0.9984 0.9946 0.9808 0.9653 0.9563 0.9585 0.9635 0.8837 1.0 0.9959 0.9866 0.9524 0.9130 0.8851 0.8770 0.8801 0.7479 2.0 0.9918 0.9734 0.9074 0.8333 0.7778 0.7507 0.7475 0.5576 5.0 0.9838 0.9480 0.8280 0.7059 0.6195 0.5718 0.5612 0.3098 10.0 0.9604 0.8790 0.6545 0.4811 0.3798 0.3280 0.3150 0.1769 20.0 0.9238 0.7838 0.4847 0.3137 0.2303 0.1908 0.1810 0.8583 0.6442 0.3131 0.1849 0.1287 0.1038 0.0977 0.0951
3.6 修理設備的失效率和更換率對系統可靠性指標的影響分析
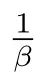
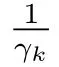
取λ1= 0.2, λ2= 0.5, μ1= 2, μ2= 1, γ1= 3, γ2= 5,圖1 至圖4 給出了以α 為自變量的δ0, A0, M 和D 的變化圖形,四條曲線分別對應于β =0.1, β = 1, β =2, β =5.從圖1 至圖4 可以看出,δ0, A0, M 和D 隨著α 的增大而減小,并逐漸趨于穩定值;另外,當修理設備失效后的平均更換時間β 越來越短時,δ0, A0,M 和D 有所增大.
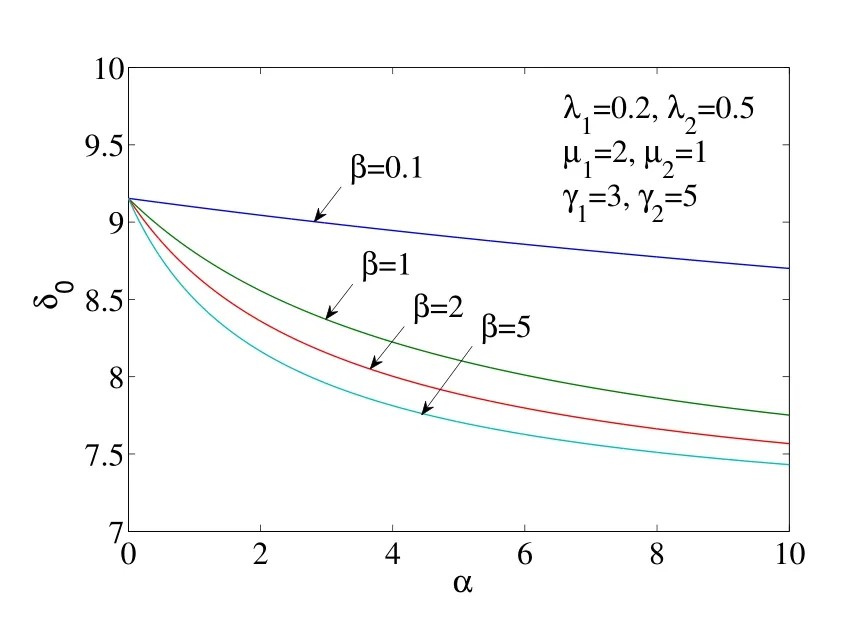
圖1: 以α 為自變量的δ0 的圖形
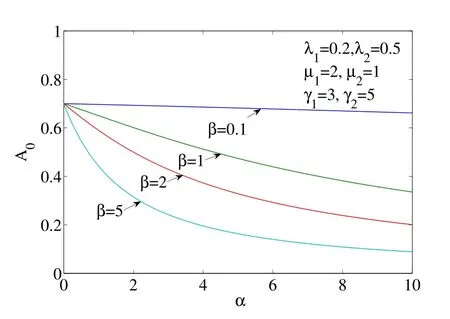
圖2: 以α 為自變量的A0 的圖形
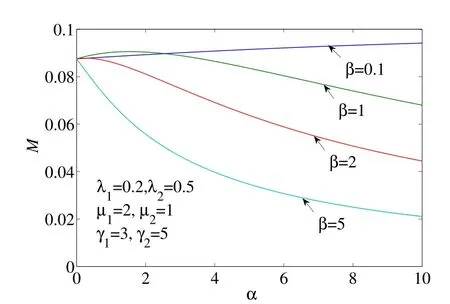
圖3: 以α 為自變量的M 的圖形
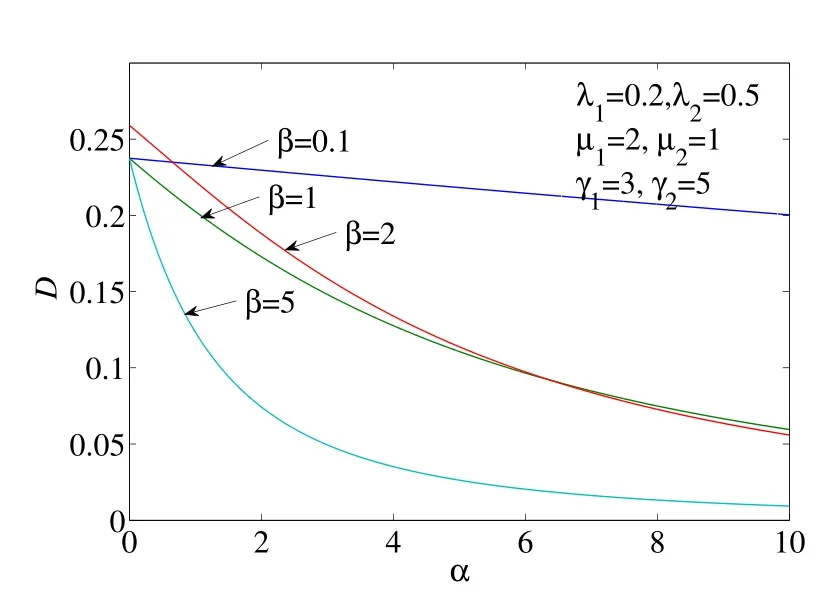
圖4: 以α 為自變量的D 的圖形
4 修理設備的可靠性指標
4.1 修理設備的閑期和“廣義忙期”
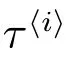

定理5對?(s)>0,則R(t)和R0(t)的LS 變換為
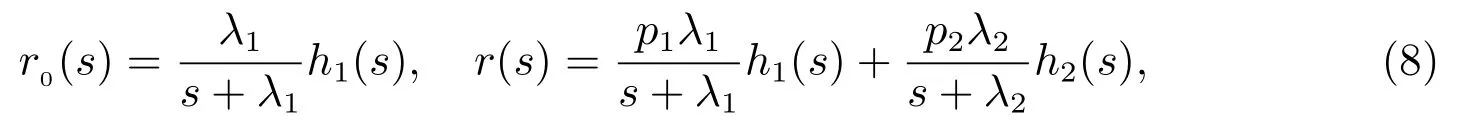
且修理設備閑期的平均長度為
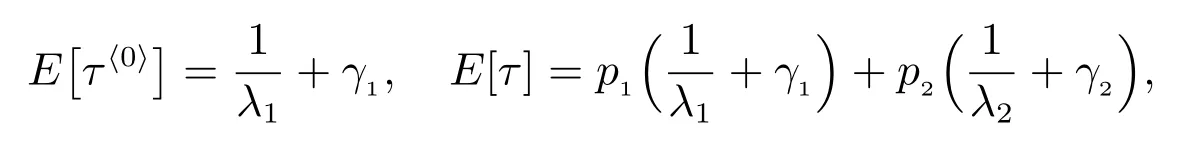
其中
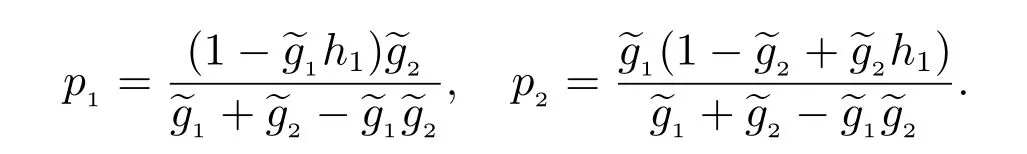
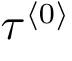
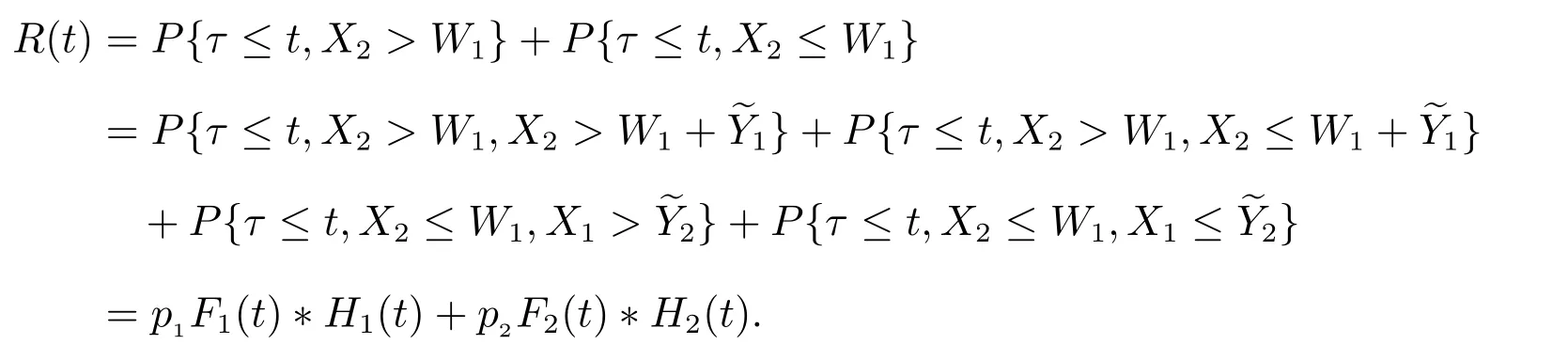
對上式作LS 變換,可得(8)式.再由
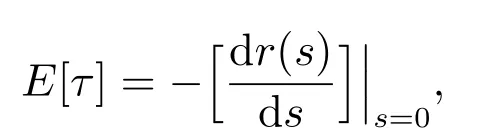
可得修理設備閑期的平均長度.
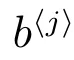
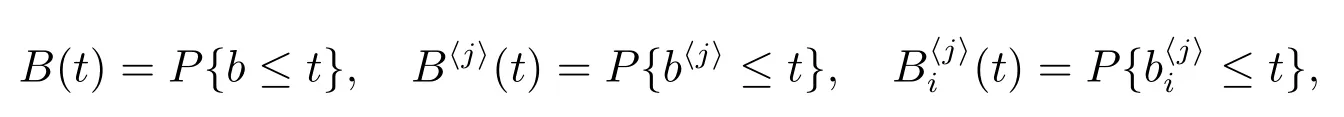
且
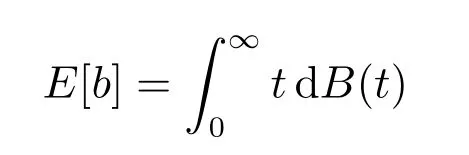
為“廣義忙期”的平均長度.
修理設備的“廣義忙期”這段時間是修理設備連續繁忙的時間,它反映了系統中修理設備的工作強度.均值E[b]表示系統經過長期運行,大約有E[b]長的時間修理設備是繁忙的,它是反映修理能力的配備是否合理的一個數量指標.
定理6對?(s)>0,則B(t)的LS 變換為
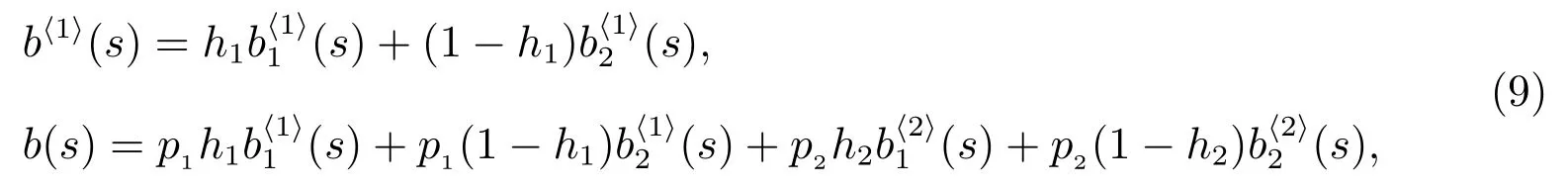
且“廣義忙期”的平均長度為
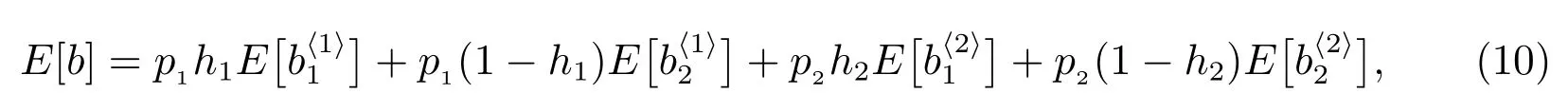
其中p1, p2由定理5 給出,
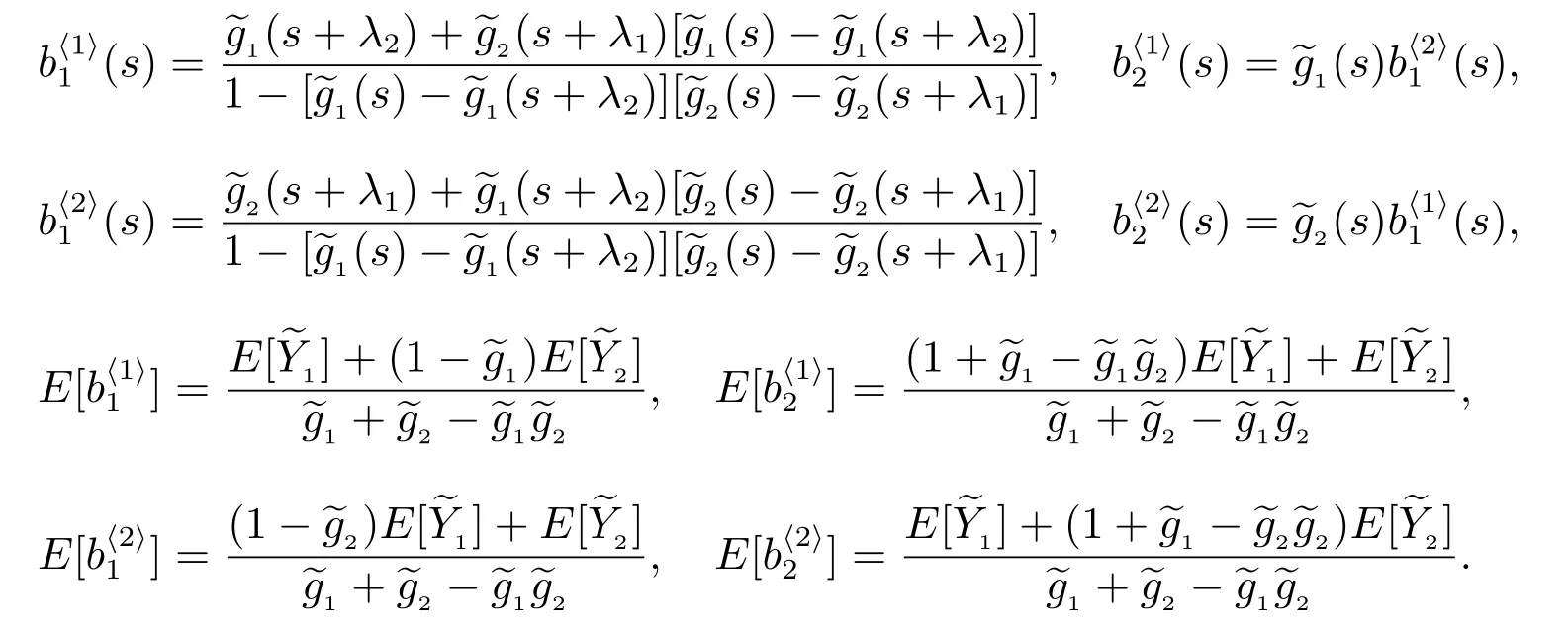
證明
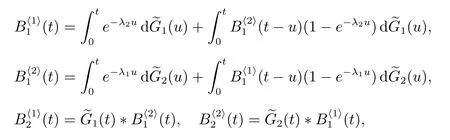
從而得
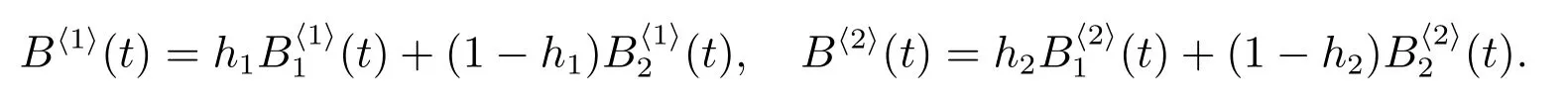
類似于定理5 的證明,可得
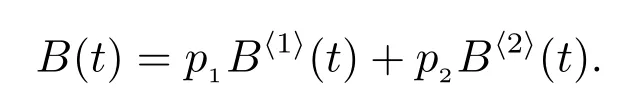
作LS 變換,得(9)式.再由
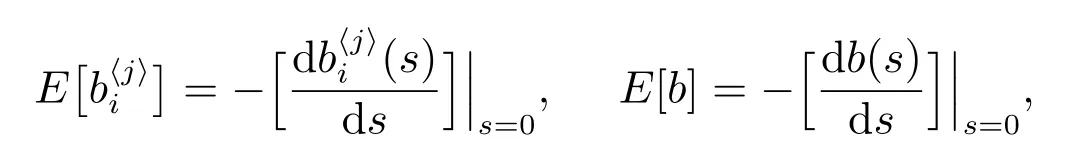
得(10)式.
對t ≥0,令

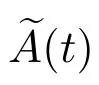
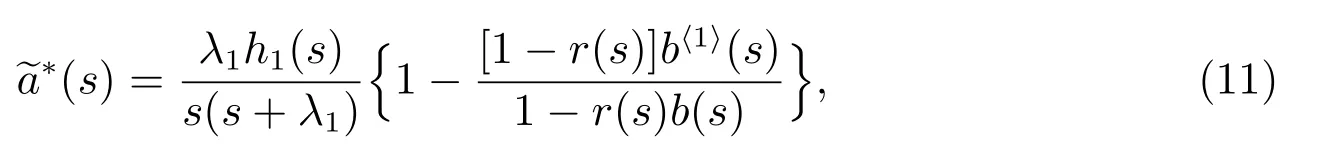
且穩態概率為
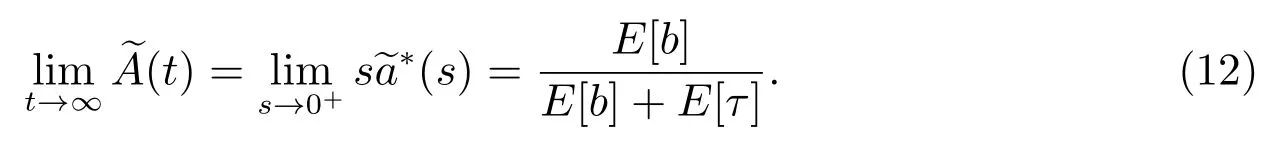
證明 根據模型的描述,修理設備的閑期與“廣義忙期”構成一個延遲交替更新過程,故根據延遲交替更新過程理論[16,17]可得.
4.2 修理設備的不可用度
由單部件組成的可修系統是最簡單的可修系統,當部件工作時系統工作,當部件故障時系統故障.假設部件的壽命U 服從參數為α 的負指數分布U(t) = 1 ?e?αt, t ≥0,部件故障后立即被修理,其修理時間V 服從任意分布V(t), t ≥0,平均修理時間為β.部件修復好后,其壽命與新部件相同,并立即進入工作狀態,進一步假設時刻0 部件是新的,且U 與V 相互獨立.對t ≥0,令
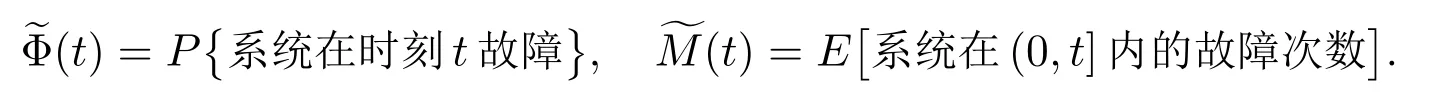
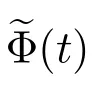

而且有穩態結果
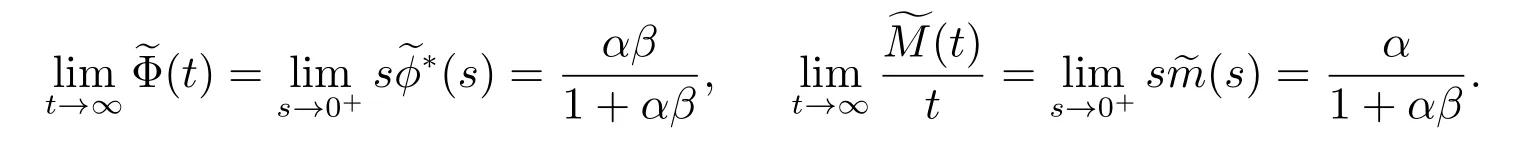
下面,我們討論修理設備在時刻t 發生失效且處于更換狀態的概率,即修理設備的不可用度.
對t ≥0,令
Φ(t)=P{修理設備在時刻t 發生失效且處于更換狀態}.
定理8對?(s)>0,Φ(t)的L 變換為
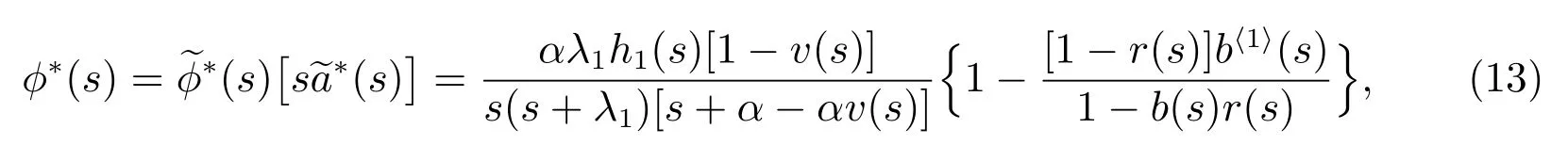
且穩態概率為
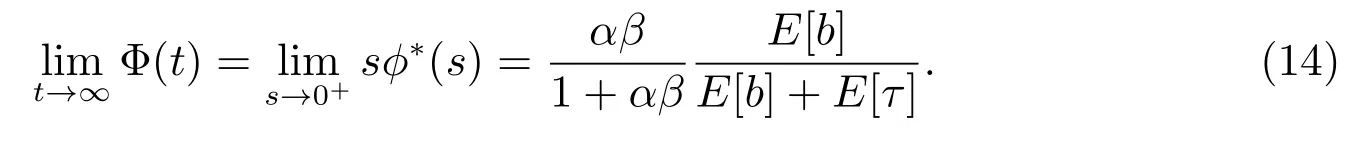
證明 1) 令τj, bj分別表示修理設備的第j 個閑期與第j 個“廣義忙期”,j =1,2,···.根據模型的描述,修理設備在其閑期內是不會發生失效的,而且在每個“廣義忙期”開始的時刻和結束的時刻都正常,其壽命仍然為U,所以修理設備在時刻t 發生失效且處于更換狀態,當且僅當時刻t 落入某個“廣義忙期”中,并且修理設備在時刻t 發生失效,從而有
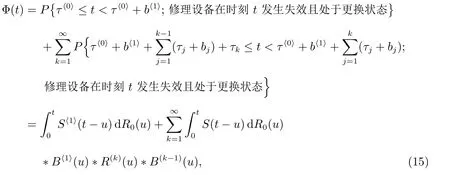
其中

S(t)=P{0 ≤t 2) 對t ≥0,有 定理9令K 表示在“廣義忙期”內修理設備修復好的故障部件數,則其概率分布函數為 且均值為 根據 定理得證. 定理10對?(s)>0,M(t)的LS 變換為 且穩態更換頻度為 證明 1) 令 則有 2) 因為修理設備僅在“廣義忙期”中發生失效,所以 對各式兩端分別作LS 變換,整理可得(17)式. 本文在由兩個不同型部件組成的冷貯備可修系統中,考慮了“修理有延遲”和“修理設備在修理故障部件的過程中可能發生失效而需要被更換”的策略,使得推廣的模型更符合實際應用背景.利用Markov 更新過程理論,得到了一些可靠性指標,并且通過數值實例分析了修理延遲時間和修理設備的失效率對相關指標的影響,使得所得的理論結果有更清晰的應用意義. 致謝:本文作者對審稿人表示衷心感謝!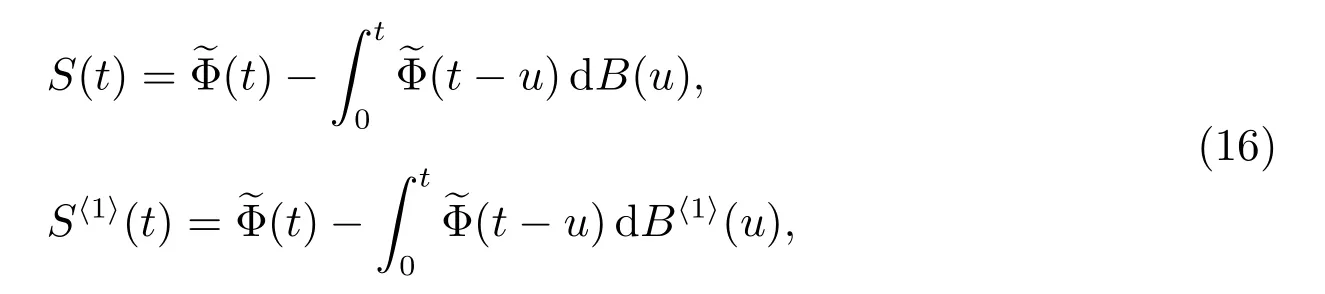
4.3 在廣義忙期內修理設備修復好的故障部件數
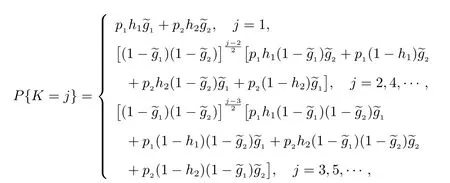
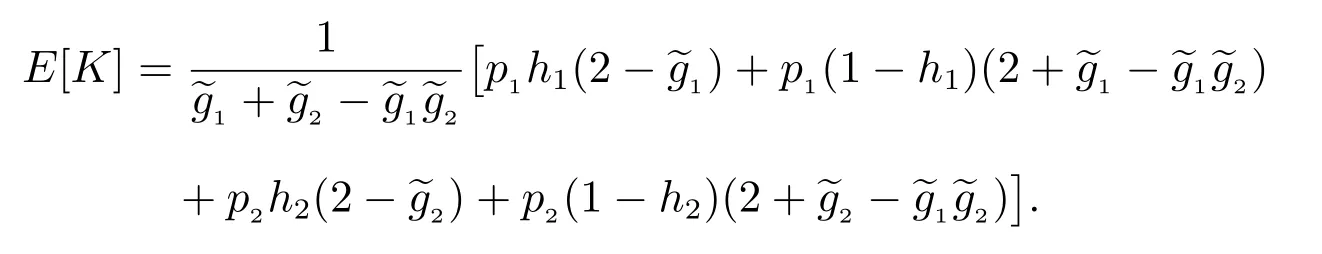
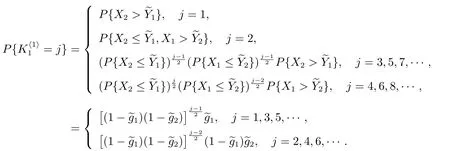
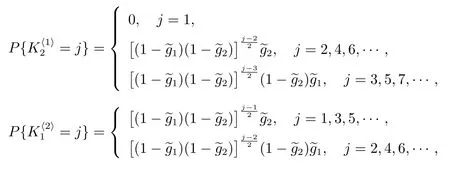
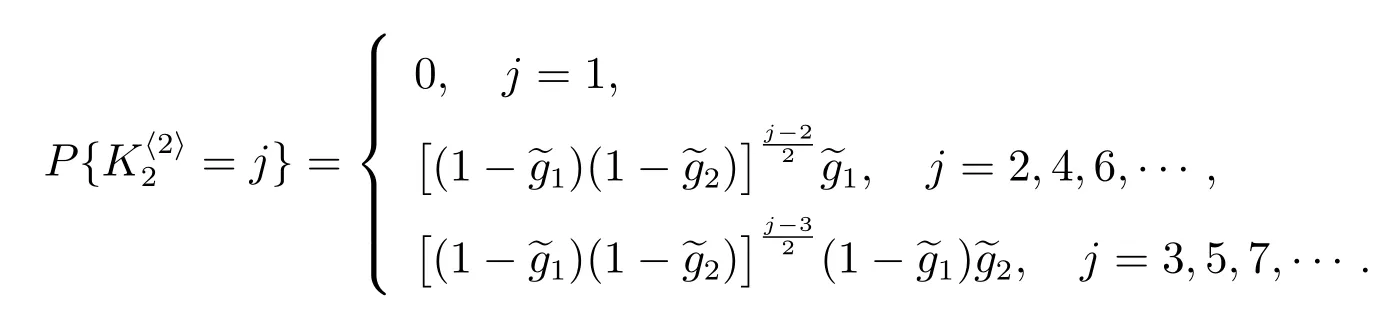
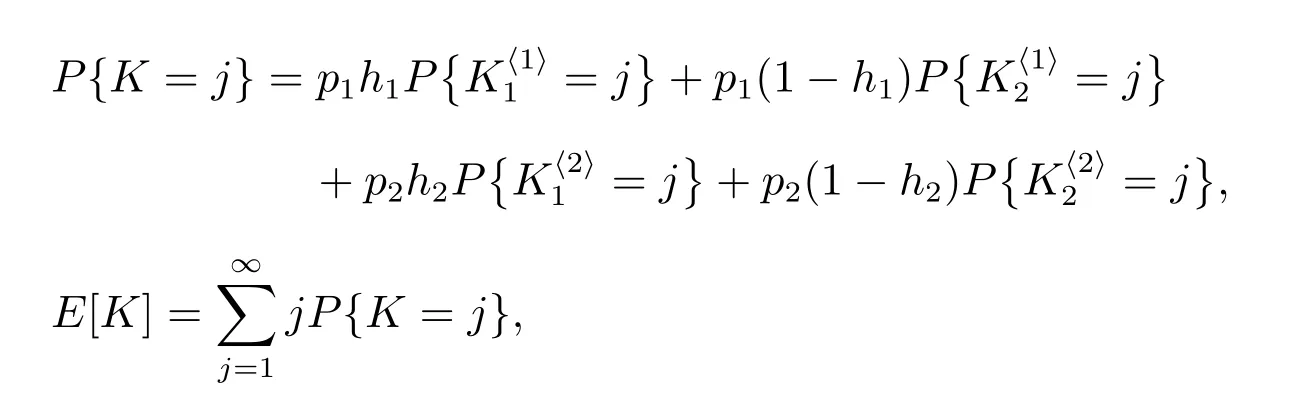
4.4 修理設備發生失效所需的更換次數
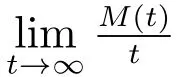
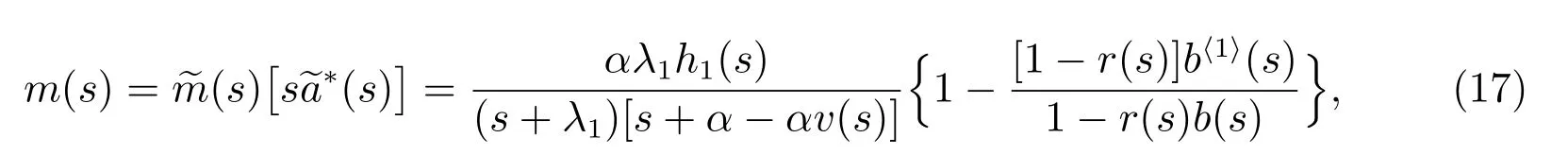
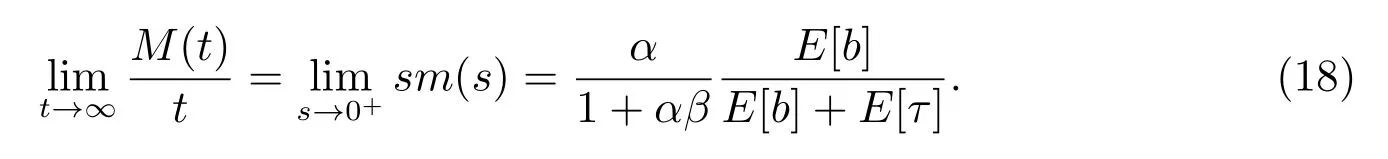

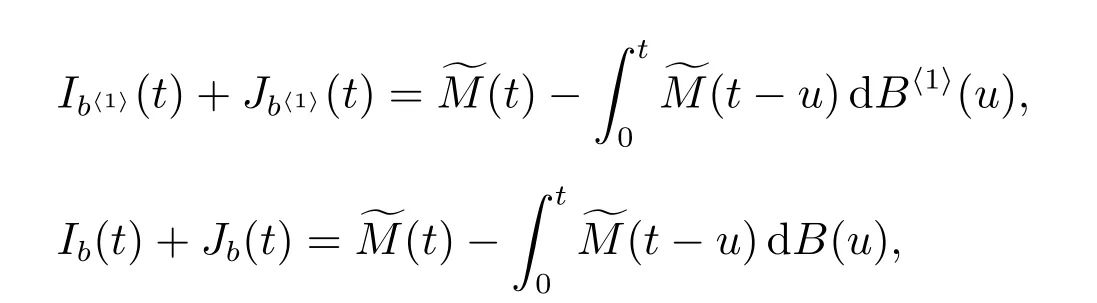
5 結論

