基于部件級三維參數化電磁模型的SAR目標物理可解釋識別方法

文貢堅 馬聰慧 丁柏圓 宋海波

①(國防科技大學電子科學學院自動目標識別重點實驗室 長沙 410073)②(航天工程大學 北京 101416)③(解放軍96901部隊25分隊 北京 100094)

1 引言

合成孔徑雷達(Synthetic Aperture Radar,SAR)具有全天時全天候獲取大范圍區域數據的能力，在偵查戰場信息方面發揮了巨大作用[1]。目前主要由經驗豐富的圖像分析師來解譯這些數據，制約了SAR在實際中優勢的發揮，迫切需要發展自動目標識別(Automatic Target Recognition, ATR)技術。

林肯實驗室于1992年發布了一種綜合的ATR系統—半自動圖像情報處理系統(Semi-Automated IMINT (IMage INTelligence) Processing,SAIP)[2]。這是一種典型的基于模板的方法，該方法將目標庫的示例數據視為模板，并根據與測試圖像最相似的模板完成對測試圖像的分類。基于模板的方法易于實現，并且當測試圖像接近或類似于模板庫中的圖像時，該方法可以獲得良好的結果。

為了保持可用于分類的目標信息并減少算法的計算復雜度，基于模板的方法通常包括特征提取過程。在這種情況下，模板和觀測圖像之間的相似性是通過提取的特征進行度量的，如何設計提取合適的特征是整個識別過程的關鍵。目前基于模板的方法所使用的特征中，一些是從光學圖像派生的傳統特征，包括幅度圖像的峰值、邊緣和紋理等。此外，有更多的特征是專門為SAR目標識別設計的。Park等人[3]根據目標的投影長度和像素提取了12種判別特征。Anagnostopoulos等人[4]使用橢圓傅里葉描述子表征目標的形狀以用于識別。此外，線性子空間、維數約減和稀疏表示等方法也被引入SAR ATR中[5,6]。Dong等人[7]提出了一種基于單演信號稀疏表示的目標分類方法。散射中心特征，例如屬性散射中心，也被證明對SAR ATR有效[8,9]。圖像以其在較低維度空間中的投影形式表示，這能捕獲目標大部分的重要特征。這類方法的例子包括主成分分析(Principal Component Analysis, PCA)[5]、線性判別分析(Linear Discriminant Analysis,LDA)[5]和非負矩陣分解[6]等。Liu等人[10]基于流形學習理論從二維圖像矩陣中提取了樣本判別分析特征。Huang等人[11]引入鄰域幾何中心縮放以構造鄰域關系，最終完成特征提取。這些方法旨在通過計算具有常數的轉換向量，將每個數據回歸到其標記向量。總地來說，在這類方法中，大部分工作集中在如何設計一組合適的特征提取器來表示目標，以及如何利用這些特征向量來訓練分類器進行識別。這些人工設計的特征提取器通常與具體數據及特定的應用背景有直接關系，并且會顯著影響識別精度。

最近對卷積神經網絡(Convolutional Neural Network, CNN)的諸多研究顯示了它們在目標分類和識別任務中的巨大優勢，并為基于學習的SAR ATR帶來了新的繁榮。CNN由兩階段架構構成：特征提取階段和分類階段。其所使用的特征不是人工設計的，而是從像素到分類器逐層學習得到的。每一層都從上一層的輸出中提取特征，然后將所有層聯合起來進行訓練。Ding等人[12]利用CNN對訓練數據進行特定域的數據增強操作(平移，散斑噪聲和姿態合成)以用于SAR目標識別。Chen等人[13]提出了一種全卷積網絡(A-ConvNets)來減少自由參數的數量，以避免由于有限的訓練圖像而導致嚴重的過度擬合。這些工作表明基于CNN的方法可以有效地學習和保留目標的二維結構信息，從而有助于提高識別性能。

盡管以上基于模板的方法很受歡迎，但是有兩個主要因素限制了其在實際情況下的性能。一方面，獲得有效的訓練數據既昂貴又耗時[14]。另一方面，這些訓練樣本無法涵蓋場景參數、目標姿態和擴展操作條件(EOC，指的是在實際戰場場景下的遮擋、掩體、連接、重新配置和多樣化的背景)下的所有情況[15,16]，這會導致識別性能的下降。

為了克服模板方法在表征目標方面的缺陷，基于模型的方法被提出。該方法通過合適的模型而不是模板來編碼目標的先驗信息。在DARPA和空軍聯合提出的具有代表性的動靜目標捕獲與識別(Moving and Stationary Target Acquisition and Recognition, MSTAR)項目[17]中，目標的散射是基于其CAD模型通過高頻計算軟件來模擬的。將在線候選目標的CAD模型預測的參考特征與從未知類型目標提取的特征進行匹配。然后，將支持或反駁候選目標的證據作為匹配分數進行累積，以確定該候選目標解釋觀測圖像的程度。最后，將未知目標判別為具有最高匹配分數的候選目標。在這種基于物理模型的表達式中，其是通過基于目標物理模型的電磁計算來模擬目標散射響應的，因而該方法還可以很容易地在線預測不同視角下的特征(例如峰值、灰度、標簽和山脊等)。而且在該方法中，目標的散射與目標的物理部分具有直接對應關系，這在目標的預測特征和其幾何結構之間保持了良好的對應關系。因此，模型可以被靈活地重新配置并添加多變的EOC背景。這些優勢使得基于模型的方法具備在現實情況下解決ATR問題的潛力。因此，基于模型的方法已成為SAR ATR的新趨勢。基于物理模型識別由于要將模型預測的散射中心與從觀測圖像中提取的散射中心進行匹配，因而導致其應用實際的一個的主要困難在于計算上昂貴的窮舉搜索步驟，特別是當預測特征集或測試特征集中存在缺失或虛假特征時。此外，當目標出現配置、連接或遮擋的變化時，模型需要重新動態建模，而且還需要大量的電磁計算。這些缺陷使該方法既耗時又效率低下。

在高頻域，一個目標的散射響應可以很好地近似為各個散射中心的響應之和[18]。散射中心模型可以對目標的電磁散射響應提供物理上相關且簡潔的參數化描述。通常，模型是精度和簡潔性之間的平衡。一方面，該模型是一個數值近似值，以適應目標在數據域中的散射響應。另一方面，該模型使得參數在物理上是有意義的。在這種基于參數化散射模型的ATR中，目標是由多個散射中心表示的，而反過來散射中心又可被用作識別目標的特征。該識別問題被視為將模型預測的參數特征與從觀測圖像中提取的特征進行匹配的問題。散射中心包含目標的位置和幅度信息，這些信息可以被視為一個屬性集。那么首先在散射中心提取階段，從參考圖像和觀測圖像中獲得可以充分描述目標散射特性的散射中心。接下來通過匹配階段來對應散射體，并根據參考圖像和觀測圖像求解兩個散射體集之間的變換關系。然后，基于散射體的匹配結果設計匹配得分。最后在識別階段，根據匹配分數將目標分類為合適的參考目標類別。具體而言，Chiang等人[19]提出了一種貝葉斯方法，其中模型預測的散射體和數據提取的散射體在匹配階段進行組合，以計算候選假設的后驗概率。其中遮擋被視為散射體丟失問題，并且散射體之間的關系被忽略了。在實際情況中，由于雜波和其他非理想因素，總是存在冗余或丟失的散射體，這使得散射體匹配成為一個難題。Zhou等人[20]提出了一種區域到點匹配的方法，該方法易于實現并且對諸如噪聲和姿態估計誤差之類的非理想因素不敏感。散射體匹配方法中存在兩個棘手的問題：首先，很難從SAR數據中提取散射體，并且可能會遺漏或錯誤地提取某些散射體。其次，當存在丟失或錯誤的散射體時，很難建立兩個散射體組之間的一一對應關系。這兩個因素可能會增加計算負擔，并降低目標識別的準確性和可靠性。此外，在某些情況下，模型中某一部件的散射可以通過幾個散射中心表示。因此，很難在模型和物理目標之間建立直接的對應關系。因此，很難更改參數化模型使其適用于重新配置的情況，更不用說知識層的推理和解譯了。

為了克服上述缺點并保持上述模型的優點，針對SAR ATR[20—24]和雷達測量[25,26]，3-D散射中心模型[21,22,27—29]被提出來，其中部件級三維參數化電磁模型(Three Dimensional Parametric Electromagnetic Part Mode, 3D-PEPM)[21,22]就是典型定位代表。在此模型中，目標通過一組屬性電磁部件(例如高帽，二面體，三面體，平板等)描述。其中散射機制和目標特性都被編碼在這些典型的電磁部件中，并且每個部件的參數與目標的物理結構有著清晰的關系。這些穩定且物理上有意義的參數可用于目標理解和推理，這使得3D-PEPM成為一個良好候選特征以用于ATR。而且，其可以以更簡單的方式模擬目標姿態和連接方式的變化，以優化EOC情況下的識別效果。因此，3D-PEPM為有望解決實際情況中多變性的部件級目標識別方法提供了一個新的方向[22]。

本文在文獻[22]的基礎上，更加詳細地描述了基于3D-PEPM的SAR ATR框架，尤其是目標識別過程中所采用的具體方法和策略。本文ATR框架主要涉及如下3個子問題：(1) 3D-PEPM到2D測量平面投影；在給定測量測試的條件下，利用3D-PEPM獲得相應的模型投影特征。(2) 3D-PEPM和觀測數據之間的相似度測量；對觀測數據進行特征提取并與3D-PEPM投影特征進行相似度計算。(3) 參數尋優。通過調整模型的參數，對當前觀測樣本與模型之間的相似度進行最大化尋優，獲得觀測數據與模型之間的真實相似度。

本文主要貢獻是基于部件級3D-PEPM的SAR ATR的理論和實驗結果。更加關注方法的可擴展性、魯棒性和在散射體的物理層面可理解的實驗結果。所提基于散射體的框架不是在整個目標層面上獲得一個匹配分數，而是針對目標中每個散射體得到一個匹配分數。所有散射體的匹配得分都用于對目標物理結構的理解。整個匹配測量過程使用了從粗到精的策略，粗層面是度量整個目標的相似性，而精層面是度量目標中各個散射體的相似性并匯總各個散射體的匹配分數，以便對整個目標進行理解和識別。這樣就可以獲得目標詳細的信息。基于3D-PEPM的ATR方法具有能提供2D SAR圖像中的特征和像素與模型上的物理幾何結構的對應信息這樣一個顯著優勢，其有助于從物理層面上理解觀測目標。

本文其余章節安排如下：在第2節中，簡要介紹了3D-PEPM，并概述了基于3D-PEPM的ATR框架；第3節討論了3D-PEPM投影問題；在第4節中，度量了3D-PEPM與觀測SAR數據之間的相似性并研究了視角調整問題；第5節介紹了使用仿真數據進行的實驗；第6節給出總結。

2 基于3D-PEPM的ATR框架

在本節中，首先簡要介紹三維參數電磁部件模型(3D-PEPM)，然后提出了基于3D-PEPM的ATR框架。

2.1 三維參數化電磁部件模型 (3D-PEPM)

在高頻區域，目標的散射場可以看作是幾個獨立散射體的散射之和[18]。在前向構建的3 DPEPM中，經驗豐富的操作人員會根據電磁理論將一個復雜目標分為多個幾何部件，復雜目標的散射響應與這些部件的散射響應關系為

其中， EModel(f,θ,φ;S)表 示目標在雷達頻率 f、視角(即仰角 θ和方位角 φ)下的散射響應。S =[S1,S2,··,Sn]是 散射體集，其中 Si包 括第i散射體的參數。 EiModel代表第i散射體的散射響應。

在本文中，前向參數化3D-PEPM嵌入了目標更多的屬性先驗信息。每個散射體的散射響應可以表示為

其中，屬性集 Si=[Ai,xi,yi,zi,αi,li]包 含了第i散射體豐富的物理屬性。 Ai表示散射體的振幅。xi,yi,zi是散射體在3D目標坐標系中的空間位置。PiModel是散射形狀函數，在不同的散射機理上有所不同。 αi表 示頻率依賴因子，li是散射體的長度。

3D-PEPM具有以下特征：

(1) 它使用參數化方法來表征目標在頻率、仰角和方位角下的3D電磁散射。當這些參數被設定后，可以有效地獲得目標在不同視角和頻率下的散射場。

(2) 目標表示為多個散射部件的組合。通過描述每個部件的散射特性，3D-PEPM可以表征整個目標的散射響應。由于這些散射體的散射與目標的物理結構密切相關，因此進行部件級的推理和識別是可行的。而且可以重新布置散射體以模擬對目標不同的操作條件，這意味著3D-PEPM具有應對目標變化的潛力。

(3) 每個散射體的散射響應對應于目標某一幾何結構，該結構涉及目標某些相關的物理屬性。那么每個散射體的屬性信息可以清晰地顯示出目標的組成，并有助于人類對目標的理解。

2.2 3D-PEPM驅動的ATR框架

基于3D-PEPM的ATR框架的流程圖如圖1所示，主要涉及3個子問題：(1) 模型投影；(2)相似度計算；(3) 視角調整。

(1) 模型投影。給定傳感器的數據采集測量參數以及包括頻率、極化、近似仰角和方位角的成像幾何，投影將產生仿真散射數據。在這一部分中，在模型散射數據生成過程中考慮了所有測量參數的情況。因此，當沒有噪聲或其他干擾時，3D-PEPM產生的數據與觀測數據相同。由于3D-PEPM由散射體組成，因此通過對3D-PEPM的投影可以獲得任意視角下單個散射體的投影信息和整個目標的投影信息。

(2) 相似度計算。通過相似度計算可以知道3D-PEPM與觀測數據之間的散射體對應關系。將3D-PEPM投影到2D圖像平面后，基于散射體的特性可檢查各個部件是否存在并評估該部件的相似度，那樣可以對目標有一個全面的了解。此外根據該模型可以直接建立數據提取的散射體和模型預測的散射體之間的對應關系，并獲得每個散射體對對應的相似度，這便給出了觀測圖像中的目標如何與3D-PEPM相似的清晰解釋。另外，由于3D-PEPM是基于目標中每個散射體的物理實體構造的，因此散射體匹配結果將更深入地揭示散射體在目標物理結構中的散射情況，從而在散射體層面解釋觀測數據。而且該基于散射體部件的方法具有噪聲魯棒性并且適用于部分遮擋的情況。

(3) 視角調整。由于雷達與目標的視角(包括仰角和方位角)只能近似估計，視角的最優估計是通過迭代不斷優化整個過程并調整視角，在3D-PEPM和SAR數據之間產生最佳的相似度測量值時得到的。

3 3D-PEPM向二維圖像平面投影

基于3D-PEPM的ATR方法的基本思想是通過散射體識別目標。每個散射體的屬性分別通過3DPEPM進行預測并從測得的SAR數據中提取出來。3D-PEPM描述了在3D空間中視角變化時目標電磁散射響應的變化，而SAR數據是在2D圖像平面中測量的。為了使這兩項具有可比性，我們引入傳感器的測量參數將3D-PEPM投影到2D測量平面，從而在2D圖像域中生成每個散射體的散射數據和特征(例如位置和散射特性)。空間位置描述了散射部件的幾何信息，而散射體形狀描述了散射體的屬性。在這一部分中，誤差校正試圖使模型產生的數據與測量數據相同，以弱化測量過程中引起的非理想因素。

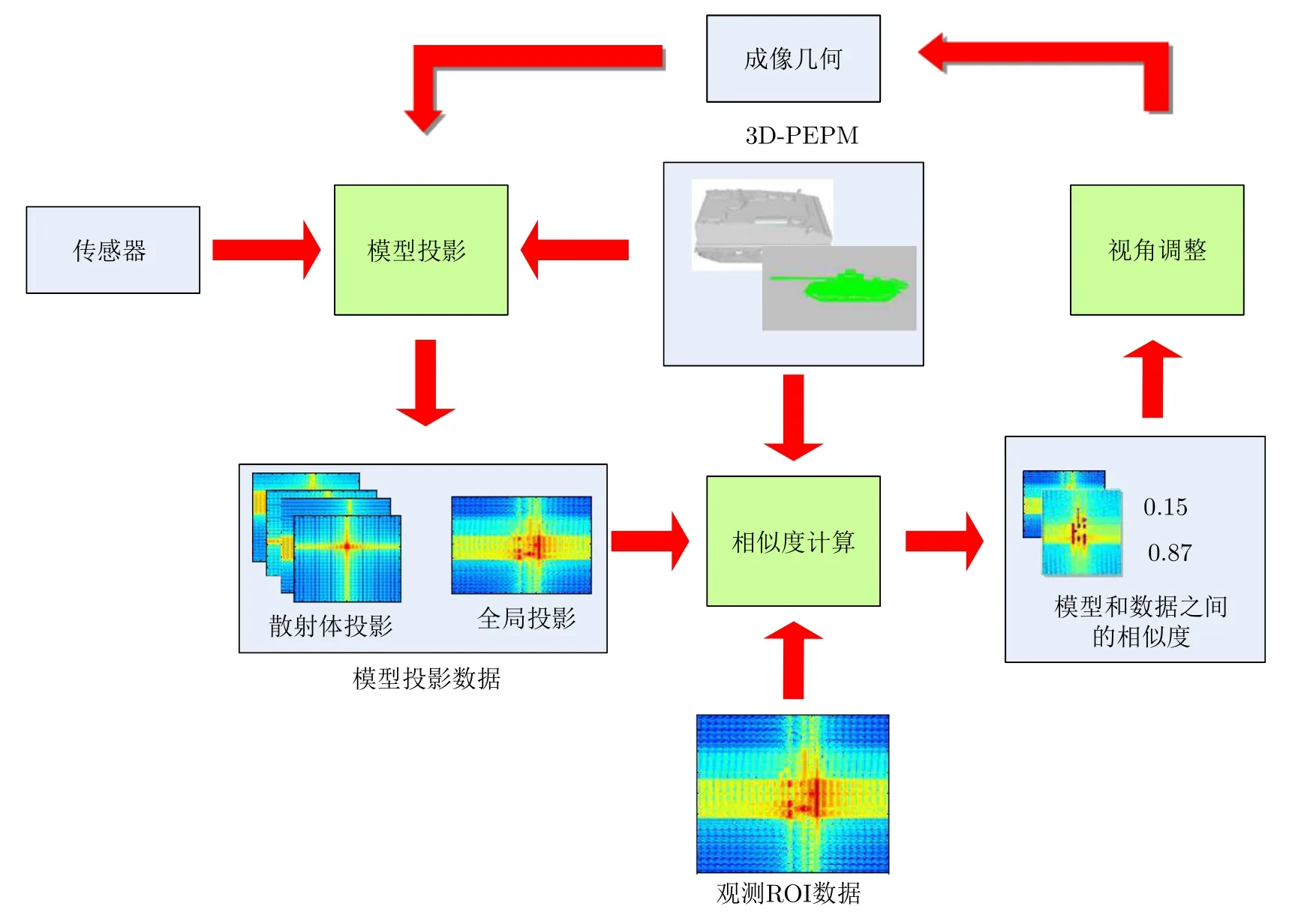
圖 1 基于3D-PEPM ATR框架的流程圖Fig. 1 The flow chart based on 3D-PEPM ATR framework

3.1 3D-PEPM的投影

圖2 顯示了在聚束模式下側視SAR的成像幾何。為了簡化討論過程，假定目標坐標系和測量坐標系一致。假設雷達沿著飛行路徑移動并在視線(Line Of Sight, LOS)方向上測量目標，那么覆蓋飛行路徑和LOS的平面被叫做成像平面或測量平面。如SAR成像幾何所示方位角為 φ ， 仰角為θ 。

目標坐標系中的一個3D點 S3D=(x,y,z)T可以通過旋轉矩陣 R投影到2D成像平面中。其中旋轉矩陣 R為

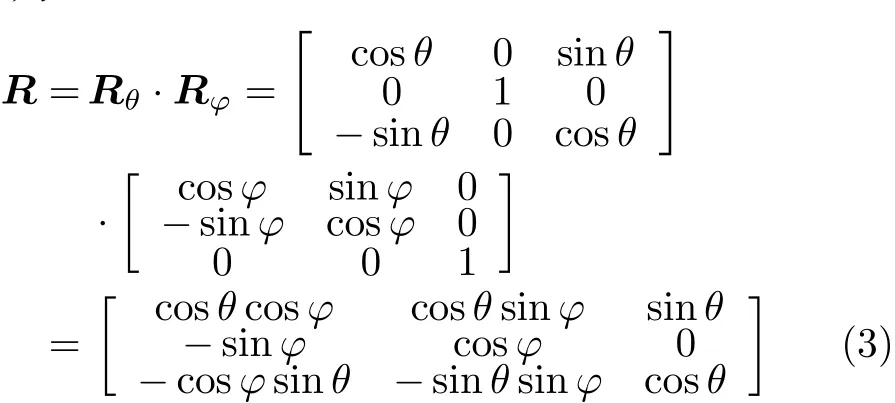
在成像平面中，將第3個坐標設置為零，則3D散射中心 S3D產 生的2D位置參數 s2D=(x2i,y2i)T可以表示為

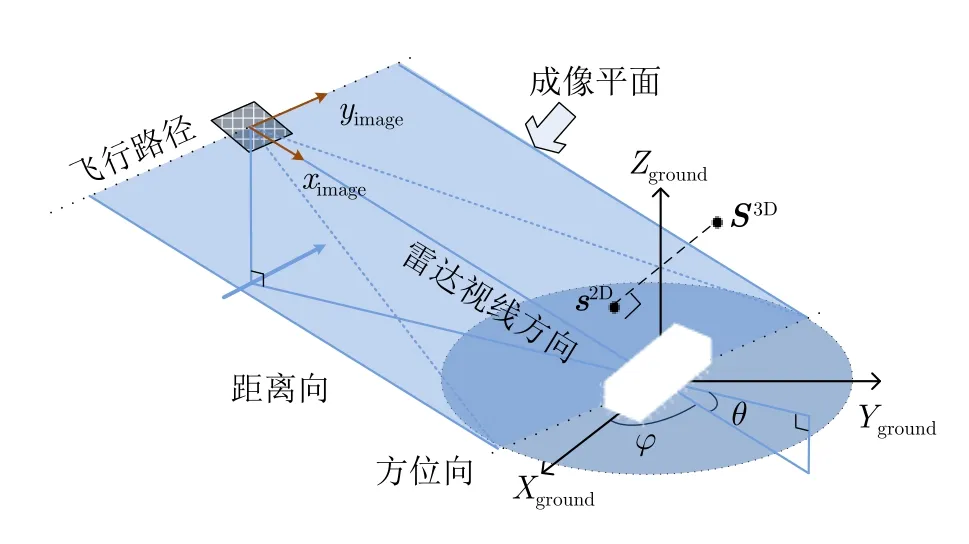
圖 2 SAR成像幾何Fig. 2 SAR imaging geometry

其中，矩陣 H表示3D到2D的投影矩陣。

對于具有一定幾何長度的散射結構而言，在不同視線下，散射中心的位置會產生偏移，故在投影中還需考慮其變化。對于半徑為 r的圓柱面散射部件而言，不同視線下，散射中心會發生位置偏移

則，圓柱面散射部件的等效散射中心坐標為

對于長度為 L的散射部件，在大側視角度范圍下表現為兩個端點處的散射點，只有在小角度下(譬如：—5°～5°)可見，理論上的投影變化關系為

為了較好地描述散射體的形狀屬性，其代表性的特征應足夠豐富以區別不同的散射體，并具有魯棒性。從理論上講，所有這些參數Si=[Ai,xi,yi,zi,αi,li]可以用于更好地描述散射體。但是 α對噪聲和雜波敏感。因此在本文方法中，引入圖像塊的能量來描述散射體的外觀，每個散射體的能量可以通過式(8)方式獲得

其中， f e2i為 在設定的成像條件下第i個散射部件的電磁散射回波能量，‖ · ‖2是l2范數。

因此，通過將3D-PEPM投影到2D平面上，可以獲得每個散射體的位置 (x2i,y2i)及其散射屬性fe2i。 投影后得到的特征用 SR={s1R,s2R,··,snR}和

3.2 誤差校正

通常通過3D-PEPM投影得到的2D圖像和通過實際飛行傳感器觀測得到的圖像之間可能會有差異。這些差異可能是由多種因素引起的：SAR傳感器的特性(包括工作模式、發射信號、天線方向圖調制)、平臺的運動(包括速度、加速度、軌跡、側傾、俯仰和偏航)、成像和后處理算法、大氣衰減、地形、測量誤差等。其中一些因素可以預先確定或在事后測量，而其他因素則是不確定的。本節將嘗試校正這些差異，提高投影圖像和觀測圖像之間的相似度，并降低兩個圖像中散射體的位置錯誤率。為此目的，針對不同情況提出了兩種方法，它們可以單獨使用或一起使用。

(1) 可量化的誤差糾正。一般情況下是可以定量測量由SAR傳感器和平臺這兩種因素引起的誤差。通過各種儀器(信號記錄儀、信號分析儀、飛行記錄儀)可以建立誤差的精確數學模型。在這種情況下，可以根據實際SAR傳感器的工作參數和工作模式，模擬從發射線性調頻信號到照射表征復雜目標的3D-PEPM以及最后接收的回波信號整個物理過程。那么仿真系統中的誤差數學模型可以用于獲得帶有誤差的3D-PEPM投影，則可以通過誤差數學模型的校正減小投影圖像和實際觀測圖像之間的差異。例如，通過仿真可以降低由SAR傳感器側傾引起的圖像失真。

(2) 不可量化的誤差糾正。對由成像和后處理算法、大氣衰減、地形、測量誤差等引起的誤差，通常無法通過數學模型對其進行建模。而且一些成像和后處理算法是沒有公開的。因此，無法通過系統仿真方法縮小由這些因素引起的誤差。在這種情況下，基于統計幾何校準和相對輻射校準，可以利用與觀測數據同時獲取的標準外部校準數據減少這一誤差。圖3顯示了幾何校準器和輻射校準器陣列的例子。

在所觀測的圖像中，與地面真實目標相比，幾何變形(目標的幾何形狀、大小、方向和其他特征)是位移、縮放、旋轉、扭曲、彎曲和其他變形的綜合結果。通過根據帶有控制點的外部校準數據對該變形進行幾何校準。在這種校準方法中，預先在SAR掃描區域內將反射器擺放在合適的位置和角度上。在測量之后，在實際觀測的圖像中找到這些反射器的對應位置。接下來，將地面真實情況下的控制點與圖像坐標系中的像素相對應。然后可以計算出變形矩陣中的各個參數。最后，根據該變形矩陣對圖像進行校準。因此根據變換函數，對于校準后的新圖像中的每個像素，可以估計出其在原始圖像上的位置。

圖 3 幾何和輻射校正陣列Fig. 3 Geometric and radiometric correction array

輻射誤差是目標電磁反射功率的真實值與其測量值之間的差。輻射校準是在給定位置區域上布置各種具有已知反向散射系數的角反射器的基礎上進行的。通過提取觀測圖像中與反射器對應的像素幅值，可以采用擬合的方法獲得輻射校準曲線。最后，對整幅圖像進行相對輻射校準。

4 3D-PEPM和SAR數據的相似度測量和視角優化調整

3D-PEPM和SAR數據之間的相似度測量是基于3D-PEPM的ATR的重要組成部分之一。本節中首先描述了測量的體系結構，然后討論了量化觀測數據與3D-PEPM匹配分數的幾種測量方法。

圖4給出了基于3D-PEPM的SAR ATR框架中3D-PEPM與數據之間相似度測量過程。我們將3D-PEPM的散射先驗信息引入到測量過程中，進而提出了一種新的3D-PEPM與SAR數據之間的相似度測量方法。首先，利用由3D-PEPM預測的每個散射體的位置和散射響應的信息，指導從2D SAR數據中提取散射體。其次，通過假設檢驗方法一一計算所有散射體對的相似度。然后將這些相似度合成為整體相似度或匹配分數。另外，整個過程增加了方位角搜索策略以用于調整視角并得到最佳相似度。這樣就獲得了3D-PEPM和2D SAR數據之間的相似度。

4.1 2D SAR數據的參數估計

根據屬性散射中心模型，可以將二維SAR數據表示為

圖 4 相似度測量框架Fig. 4 Similarity measurement framework

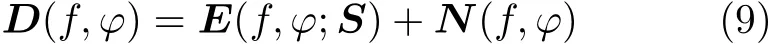
其中， E (f,φ;S)代 表模型項， S =[S1,S2,··,Sp]表示 p個散射體； N (f,φ)表示噪聲項，其被建模為高斯白過程。

散射體參數估計的表達式為[8]

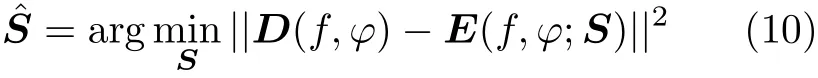
本文使用近似最大似然(Approximate Maximum Likelihood, AML)算法從觀測圖像中提取散射體。AML算法的詳細描述可以參考文獻[8]。然后，從觀測圖像中得到的第i散射體的估計參數集為Si=[Ae,xe,ye,Le,αe]T。

4.2 相似度測量

在3D-PEPM與SAR數據之間的散射體相似度測量過程中，一些準則應該被考慮：

(1) 每個散射體的位置和屬性參數都應用于相似度的測量，因為與其余參數相比，這些參數具有更高的可靠性。

(2) 相似度測量方法應足夠魯棒，以應對3DPEPM與觀測數據之間可能存在的不一致問題。

(3) 散射體與目標物理部分之間的對應關系應該用于基于知識的目標識別。

基于上述準則，本文提出了幾種相似度測量方法。接下來將逐一介紹這些方法。

(1) 基于散射體區域特征的相似度測量。每個散射體的散射響應在頻域和圖像域均不相同。在這一部分中，我們將通過圖像域中的散射響應來評估每個散射體對的相似度。為了較好的利用和描述散射響應，我們定義了散射主能量區域和第2能量區域為

在圖像中，主能量區域 Rm覆蓋了大部分散射能量，而第2能量區域 Rs描述了較弱的散射。假設這兩個區域的散射共同表征了一個散射體的散射。在實驗中，設定 η1=90% 和η2=90%。

此外，根據這些區域定義了一個散射對的相似度為

其中， fe 是 測量圖像的能量， fRs是測量圖像中區域 Rs的 能量，σe是控制參數。

(2) 基于假設檢驗的相似度測量。假設檢驗是統計數據分析中的重要工具[30,31]，可用于判斷樣本是否來自特定的概率分布。對具有給定屬性的目標稱之為零假設 H0， 相反的是另一種假設 H1。假設目標服從均值為 μ0且 方差為 σ0的正態分布，對其有n個觀測樣本且均值為 xˉ ， 檢驗統計量計算為|z|=這里 C是由顯著性水平 αS(0 ≤ αS≤ 1)確定的閾值。

這一方法將單個散射體對的相似性評估轉換為假設檢驗問題。這里零假設設置為“SAR圖像中存在模型預測的散射體”。然后為每個參數建立統計模型并計算檢驗統計量以確定假設檢驗的結果。概率 p設置為單個散射對的相似度f (si)。考慮到參數αi對 噪聲和雜波敏感，我們僅使用 Ai,xi,yi,li參數并且它們的高斯分布參數如表1所示。

對于目標的整個圖像，散射體根據模型中的能量從最強到最弱排序。之后，依次對每個散射體對執行假設檢驗。當通過假設檢驗確認某個散射體對的相似度時，將其散射響應從圖像中移除以避免其干擾其他散射體。

表 1 參數的統計模型Tab. 1 Statistical model of parameters

4.3 相似度合成

應當基于所有散射體的相似度來合成整個目標的相似性。可以使用不同的方法來實現此目的。這里我們提出以下3種簡單而有效的策略：D-S證據規則，求和規則和SVM訓練規則。

(1) D-S證據規則。D-S證據理論是一種可將不同來源的信息進行組合并做出更可靠決策的經典方法[32,33]。因此，其可以用來組合來自不同散射體的相似度，其中每個散射體的相似度均作為證據。每個散射體的相似度 f (si)都是D-S融合中的基本概率分配值。在給定視角下，3D-PEPM和SAR數據之間的組合相似度為

(2) 求和規則和SVM訓練規則。另一個直觀的想法是將各個散射點的相似度相結合，通過對它們進行求和來產生全局相似度

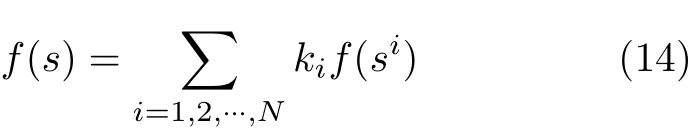
其中， ki是 散射體i的權重系數。該計算公式可以是不加權平均(即 ki=1/N)，也可以根據各個散射體的重要性為權重系數分配不同的值。

權重值也可以以使用最大利潤率SVM框架從驗證樣本中獲得的分數為依據學習得到。給定具有部件匹配得分的正驗證樣本 SP和 負驗證樣本 SN，我們希望通過最小化如下結構化的預測目標函數學習得到權重k i[34]

在訓練過程中，限定權重 ki＞ 0.001。權衡參數 W通過5重交叉驗證得到。這個問題可以通過標準的優化軟件包來解決。學習得到的結果 ki可以看作是部件對于判斷目標存在的權重貢獻。

至此得到了一個視角下的3D-PEPM和SAR數據之間的相似度。在實驗中使用了D-S證據規則并獲得了令人滿意的結果。

4.4 視角優化搜索

觀測仰角 θ可以根據雷達平臺的飛行高度及雷達與目標之間的距離近似估算，可以認為是已知值。而從觀測圖像估計的方位角可能與其真實值有一些差異，分別用 a zi0和 Δ azi表示估計的方位角和估計誤差。本文在一個方位角范圍[azi0-Δazi,azi0+Δazi]內計算目標的相似度。在每個方位角azik(azik∈[azi0-Δazi,azi0+Δazi])，計算得到一個相似度 mk。 選擇產生最高相似度 mp的方位角azip作為最佳視角，并將3D-PEPM與2D SAR數據之間的相似度設定為 mp。

從目標識別的角度來看，可以將相似度用作3D-PEPM和2D SAR數據之間的匹配分數。當相似度高于預設閾值 fH時，將模型視為候選類型，即它可能是觀測數據中的未知目標的類別。相反，如果相似度低于預設閾值 fL，我們認為觀測數據中的目標與模型無關。當觀測圖像與一個模型匹配而與其他模型顯著不同時，將觀測樣本指定為模型對應的類別是合理的。

5 實驗

5.1 實驗設置

(1) 3D-PEPM 。3D-PEPM是基于如圖5所示的目標CAD模型以前向的方式構造的。目標由具有理想散射特性的簡單散射體(三面角、二面角、頂帽和平面)組成，如圖6所示。通過比較模型生成的散射數據和基于電磁仿真軟件計算得到的CAD模型的散射數據，可以驗證3D-PEPM的有效性。這兩個模型對應的數據集的RCS對比如圖7所示。不同視角下基于3D-PEPM生成的SAR圖像如圖8所示。

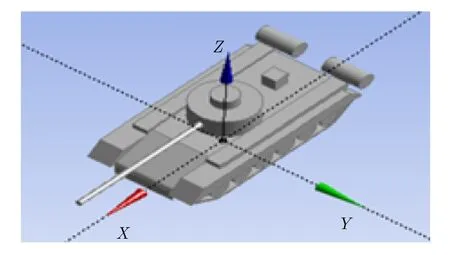
圖 5 簡易坦克的CAD模型Fig. 5 CAD model of the simple tank

(2) 觀測SAR數據。EM仿真軟件利用目標的CAD模型產生的仿真散射數據被設置為觀測數據，其被用來說明本文算法的整個處理過程并驗證算法的可行性。本實驗使用了3種CAD模型。與3D-PEPM具有相同目標類型的坦克模型用于檢測算法的正確識別率，與3D-PEPM不同目標類型的裝甲車模型和slicy目標模型[2]用于檢測算法的虛警率。仿真所使用的雷達信號是一個步進頻率脈沖信號，其中心頻率為f0=9 GHz，頻點數為M=101且頻率間隔為10 MHz。合成孔徑的方位角角度范圍為5°，角度個數為N=101，則角度間隔為0.05°。給定中心方位角 φ 和 仰角 θ，可以生成一個SAR圖像數據。在實驗中， θ在[20°～28°]范圍內以2°等間隔取值，φ在[5°～160°]范圍內以5°等間隔取值，那么每種模型都有 5 ×32=160幅觀測圖像。圖9顯示了這些數據集中在相同視角下3個模型的圖像。

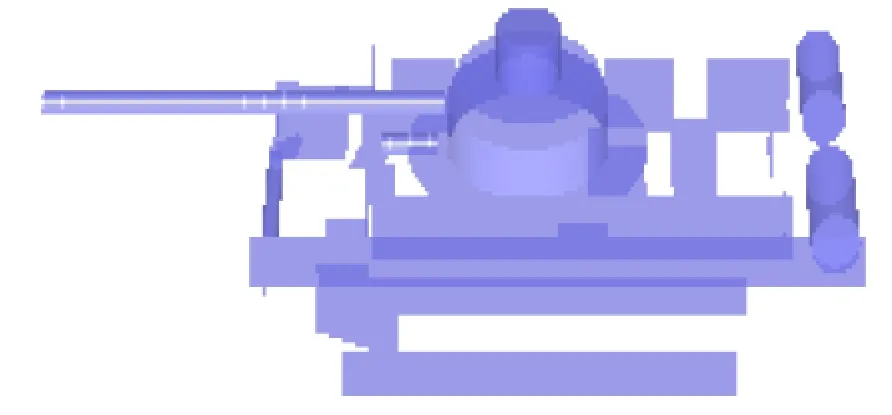
圖 6 簡易坦克中的散射體Fig. 6 Scatterers in the simple tank

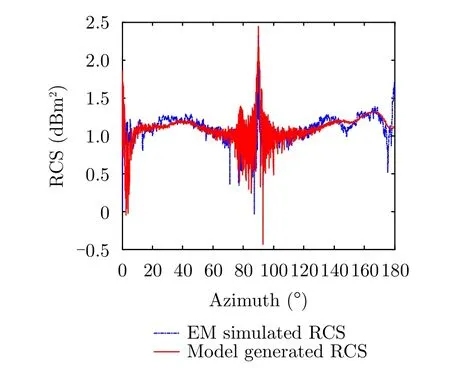
圖 7 模型和EM仿真軟件產生的目標RCS對比Fig. 7 Comparison of target RCS generated by 3D-PEPM and EM simulation software

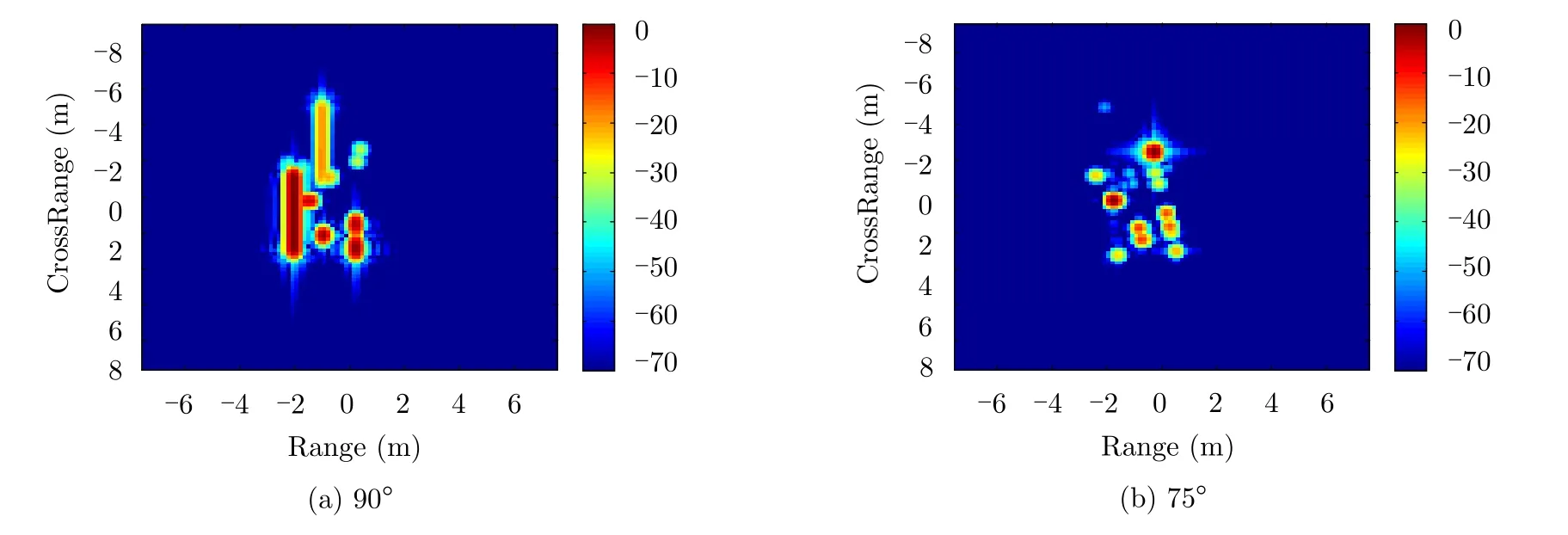
圖 8 不同視角下基于3D-PEPM生成的圖像Fig. 8 Images generated from different perspectives based on 3D-PEPM

5.2 實驗結果

本節測試了不同情況下基于3D-PEPM的ATR方法的性能。通過假設檢驗方法計算單個散射體的相似度，并使用D-S證據方法來合成整個目標的相似度。

(1) 理想情況下的相似度測量。圖10(a)顯示了θ= 3 0°和 φ=90°在坦克目標的仿真圖像。表1列出了假設檢驗中各參數的統計模型。實驗中將顯著性水平和檢驗閾值分別設置為0.05和1.96。給定的姿態下，共有10個可見的散射體。表2對比了從3D-PEPM投影得到的散射體參數與從對應觀測數據估計得到的散射體參數，同時也列出了它們的相似度。由表2可知，3D-PEPM中的散射體可以以很高的概率在觀測數據中找到其對應部分。在特定視角下，模型中大多數的散射體的相似度超過了0.5，并且根據式(13)計算得到的融合相似度為0.752。

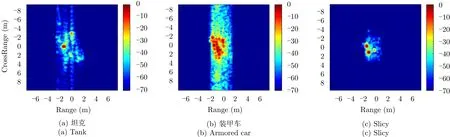
圖 9 相同視角下3個模型的觀測圖像Fig. 9 Observation images of three models in the same perspective

3D-PEPM中的散射體與目標中的實際物理部分相關。如圖10所示，基于模型得到的圖像中的像素與坦克目標的表面是有關的。圖11給出了一個更加直觀的例子，模型圖像中編號為1的散射體對應于目標中編號為11的二面角；模型圖像中編號為5的散射體對應于目標中編號為5的圓柱體。這樣，可以建立物理模型與觀測SAR數據之間的聯系，有助于理解和推理被觀測的目標。

通過基于模型的目標識別方法的處理流程，與三維電磁散射模型匹配得到的相似度結果如圖12所示。從該結果可以看出3類數據在相似度上有著較大的差異。其中，坦克目標的相似度較高，而裝甲車目標和SLICY目標的相似度一直保持在較低的水平，這也與實際情況是相符的。最終確定目標的類別時，當匹配度大于給定的閾值，可認為該測試目標與模型所表示的目標類別是相同的。否則，測試目標與模型的目標類別不一致。在設定閾值fT=0.35的條件下，160幅坦克測試數據中的156幅數據被正確識別為模型目標類別，同時160幅裝甲車數據中的153幅數據和所有的SLICY數據被正確識別為不屬于模型所表示的目標類別。

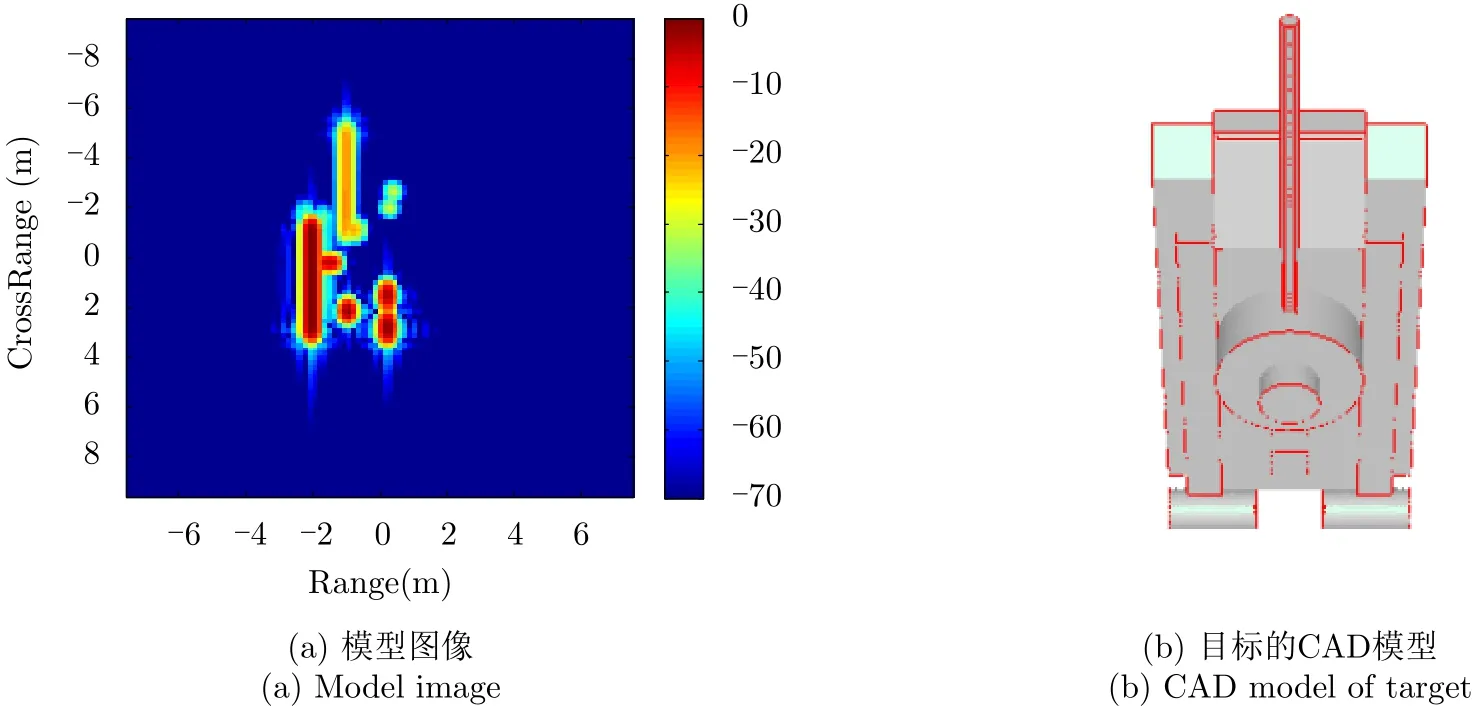
圖 10 模型圖像和3D-PEPM物理相關的散射體Fig. 10 Model image and 3D-PEPM physically related scatterers

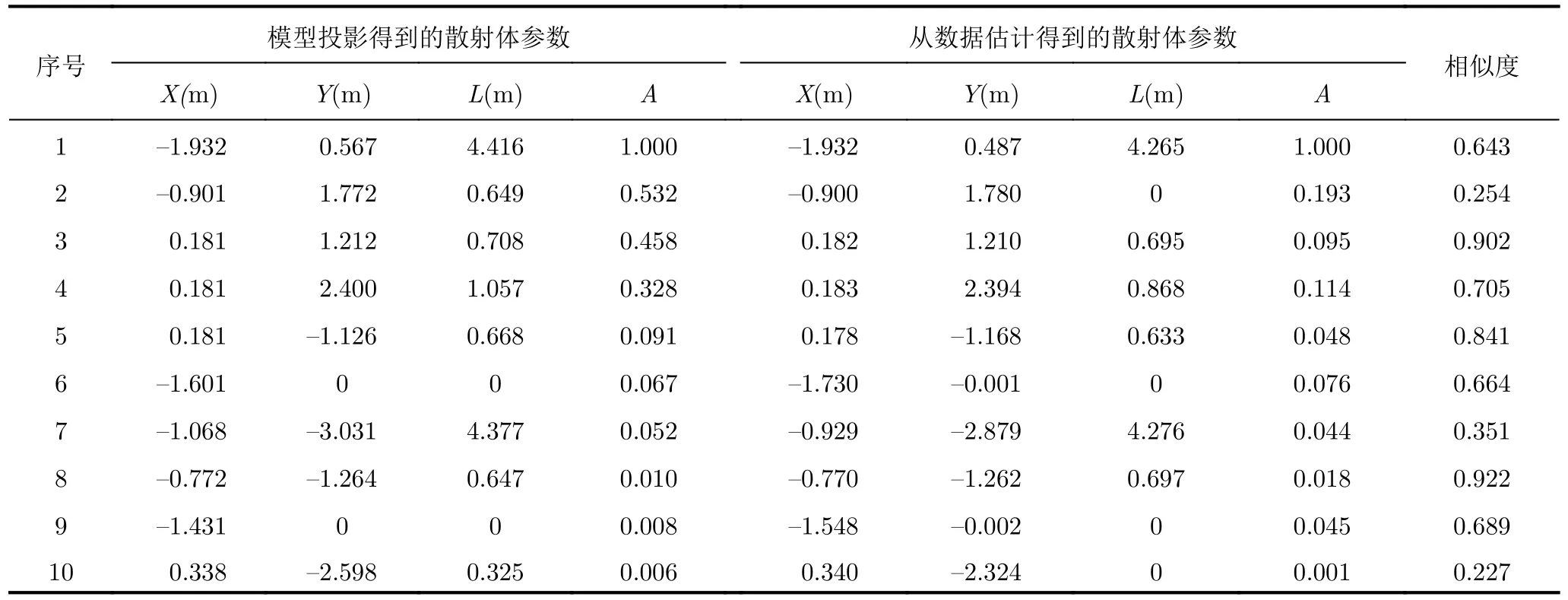
表 2 模型投影和從數據估計得到的散射體參數的對比Tab. 2 Comparison between model projection and scatterer parameters estimated from data

圖 11 模型圖像和3D-PEPM物理相關的散射體Fig. 11 Model image and 3D-PEPM physically related scatterers

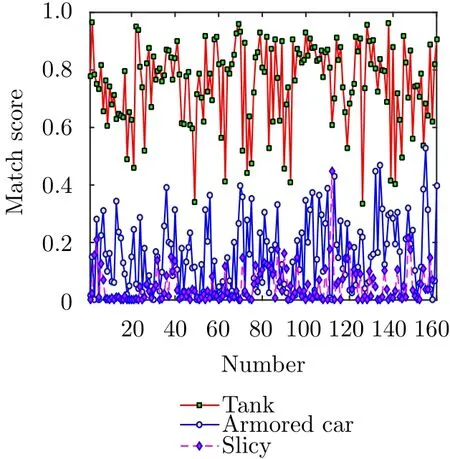
圖 12 相同視角下3個模型的觀測圖像Fig. 12 Observation images of three models in the same perspective

(2) 存在噪聲情況下的相似度測量。這一部分檢驗了存在噪聲情況下本文算法的相似度測量性能。通過將高斯白噪聲添加到原始仿真圖像中，可以獲得含噪聲的圖像。將信噪比(SNR)水平設置為{40, 30, 20, 10, 5, 0, —10, —15, —20} dB，其中信噪比的定義為

其中， r( w,h)代 表SAR圖像的頻域數據， σ2為噪聲方差。圖13顯示了slicy目標在某些噪聲下的圖像。圖14給出了在不同噪聲水平下的相似度。從圖14中可以看出當SNR超過—10 dB時，相似度保持在較高水平，這驗證了所提出的相似度測量方法對噪聲的有效性和魯棒性。

(3) 存在遮擋情況下的相似度測量。本節通過實驗檢驗了存在遮擋情況下本文算法的相似度測量性能。通過丟棄在 θ = 30°和 φ=90°下觀測圖像中的一些散射體，模擬得到了被遮擋的SAR圖像。如圖15所示的相似度測量結果，當少于兩個散射體(總共9個散射體)被遮擋時(剩余散射體的能量為41.40%)，相似度仍能維持在很高的水平。但是，當丟棄3個或更多散射體時(剩余能量少于23.53%)，相似度急劇下降。從圖15結果說明，即使遮擋了總圖像能量的58.60%，所提相似度測量方法仍能很好地發揮作用。

6 結束語

圖 13 Slicy目標在不同信噪比下的仿真圖像Fig. 13 The simulated images of the slicy target under different SNR

本文提出了一種基于3D-PEPM的SAR目標物理可解釋的識別方法。在此方法中，目標被視為多個散射體的組合，并且其先驗信息被編碼在3D-PEPM中。目標識別任務是通過測量3D-PEPM和2D SAR數據之間的相似度完成的。在3D-PEPM模型的指導下，這種相似度的測量更具針對性并且有較強的抵抗噪聲干擾的能力。而且在散射體層面的相似度測量方法中，即使在觀測圖像中未發現一些散射體，也可以可靠地完成相似度的測量。另外，基于相似度測量的結果，可以通過散射體對之間的對應關系獲得目標組成部分的信息，這有助于對目標進行理解和推理。論文采用了簡易坦克的仿真數據驗證了該方法的有效性和魯棒性。由于數據保密問題，我們在實際SAR載荷獲取的實際目標數據上的方法有效性驗證結果并未展示。

圖 15 散射體遮擋下的相似度測量性能Fig. 15 Performance of similarity measurement under scatterer occlusion