海雜波背景下雷達目標特征檢測方法的現狀與展望

許述文 白曉惠 郭子薰 水鵬朗

(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)

1 引言

我國擁有長達1.8×104km的海岸線和3×106km2的藍色國土，島礁星羅棋布，領海、專屬經濟區、大陸架的無縫監控和管理成了建設海洋強國的首要任務之一。隨著我國建設海洋大國基本國策的確立，海面監視對于海洋國土保護起到越來越重要的作用。各種類型的雷達系統構成了實施海環境全天候、全天時監控的主要裝備。利用雷達技術對海面進行觀測是實現海面動態監測以及海面目標預警監視的一個重要手段。隨著雷達對海觀測在軍事科技領域的廣泛應用和在民事領域的迅速發展，針對海面電磁散射回波的研究也受到人們越來越多的重視。研究復雜海面回波信號的主要目的通常有兩種：一是從海面的回波信號中提取反映海洋動態特性的信息(例如浪高、浪向、風速等)；二是從復雜海面回波信號中探測出目標(例如船只、浮冰、飛機等)，此時海面回波信號便是一種干擾因素，通常被稱為海雜波。

海雜波定義為雷達電磁波照射到海表面時接收到的海表面后向散射回波[1—4]。海雜波產生的物理機理復雜，依賴于很多因素，其中包括了復雜海面本身的狀況以及雷達的工作狀態。由于受到環境因素和雷達設備參數的影響，海雜波的特性也不斷改變；相較于地面雜波，海雜波的空時變化要更為復雜。目前，海面微弱目標檢測面臨的主要困難來自于4個方面：

(1) 慢速小目標回波微弱。小型船只、冰山、蛙人、碎片、潛艇潛望鏡、隱身目標等海面小型目標有很小的雷達散射截面積(如圖1所示)。由于回波較弱，這些目標在常規雷達中具有非常低的信雜比(Signal Clutter Ratio, SCR)。雖然海上反入侵雷達設計成高的空間和多普勒分辨率，以便將SCR提升到臨界值使得感興趣的目標可檢測，但即便如此，在低SCR情況下傳統檢測方法依然很難進行檢測。同時，由于目標運動速度較慢，且海雜波具有較寬的多普勒帶寬，目標和海雜波在多普勒上很難區分，因此這類檢測通常被稱為“超雜波檢測”。傳統的自適應類檢測方法在這種情況下很難奏效。

圖 1 常見的海面小目標Fig. 1 Some common small targets on the sea

(2) 空時變海雜波異常復雜，海雜波特性認知難度大。雷達系統的距離方位以及多普勒的高分辨率觀測使得海雜波已然不滿足于傳統的大尺度下的統計特性，具有更加復雜的特征。受海洋氣象、地理環境等諸多因素的影響，海面非線性隨機變化，機理非常復雜。同時，海浪隨風速的增加而增高，在重力作用下，當海浪失去平衡狀態時產生破碎波，而在海浪徹底破碎之前的“劈結構”使得其出現類鏡面反射，從而出現較強的回波，即為海尖峰[3—8]。而與目標特性極其相似的海尖峰分量的出現，使得雜波的建模變得異常復雜[9,10]。同時，隨著我們的關注點從近岸轉向遠海，對海雷達必須對一定范圍的陌生海洋環境進行監控和偵查。海雜波的“三非”特性，也就是非均勻、非平穩和非高斯特性更加明顯。如圖2(a)所示，海雜波的功率圖呈現出很強的非均勻和非平穩特性。如圖2(b)中所示，雜波的經驗概率密度函數嚴重偏離了瑞利幅度分布，呈現出明顯的非高斯特性。強烈的非均勻和非平穩特性意味著海雜波的特性僅在臨近的距離-方位分辨單元可以認為是保持不變的，而隨著空間距離的增加，海雜波的同分布程度大為下降。雖然海雜波在慢時間維的特性變化比較緩慢(與氣象條件和海況變化的時間尺度同階)，但大場景掃描觀測雷達缺乏長時間駐留觀測的時間資源，從而很難在慢時間維上獲取大量獨立同分布樣本。也就是說，雷達對海探測雖然可以得到整個場景下大量的海雜波數據樣本，但估計一個雷達分辨單元的海雜波特性時，完全獨立同分布的樣本只有局部的、短時間區間內的小數目樣本。因此，海雜波特性感知本質上是一個“小樣本”問題，我們稱之為“本性小樣本”問題。同時，由于大場景海雜波的特性是空變和時變的，因此必須實時在線感知大場景中隨著空間和時間變化的海雜波特性，才能實現真正意義上的恒虛警檢測。

圖 2 實測數據功率圖及幅度擬合結果Fig. 2 Power map of measured data and amplitude fitting results

(3) 目標模型難以建立。大型船舶的運動和姿態幾乎不受海浪的影響，而海面小目標的運動和姿態會受到海風和海浪的嚴重干擾。由于海面小目標的復雜運動模式(包括橫滾、俯仰、偏航等)，目標甚至會在某段時間里，部分或全部被海浪遮擋，因此小目標回波具有嚴重的RCS起伏及復雜的振幅和多普勒調制現象。海面目標的種類多種多樣，通常可以分為以下3類：第1類是海面上空低空掠行的目標，這類目標運動速度快，機動性強，能夠被雷達有效地檢測；第2類是海面上的大型目標，如大型艦船、游輪等，這類目標的實際物理尺寸較大，RCS較大，也能夠被雷達有效地檢測；而第3類就是海面上的漂浮小目標，如飛機殘骸、蛙人、潛望鏡等，這類目標的RCS小，并且雷達回波常常會被淹沒在海雜波中，不容易被檢測，屬于海面低可觀測目標，如何有效地對海雜波背景下的海面低可觀測目標進行檢測是研究人員一直在探索的問題[12,13]。因此，在所有情況下建立類似于自適應檢測類方法中目標的簡單參數模型來描述感興趣目標的回波是困難的，必須發展新的特征檢測方法。

(4) 目標、海雜波類別非平衡。在對海觀測中，海場景較大，而在海面上游弋的微弱小目標相對海面回波卻數量有限。因此，獲取的大量數據中，絕大部分的數據均為海雜波回波數據，而目標回波數據的數據量遠小于海雜波，這在機器學習和模式識別中，稱為“類別非平衡問題”，這個現象造成的原因在于目標相對于海雜波的稀疏性。傳統的模式識別和機器學習中的方法對于處理類別非平衡問題，會出現分類性能下降的情況。因此，傳統機器學習方法在海雜波背景下微弱小目標檢測上也同樣面臨著挑戰。

由于目標類型的不斷出現和雷達體制的不斷變化，對海微弱小目標雷達探測是一個長期的話題，經久不衰。隨著雷達體制的變革和新的信號處理技術手段的出現，對海目標雷達探測領域涌現出了許多新問題和針對這些問題的新方法。本文首先總結一下目前常用的對海目標雷達檢測的方法。然后，作為對海目標智能檢測算法評估的一個重要組成部分，本文介紹了目前常用的用于設計和測試特征檢測方法性能的數據集，并逐一介紹了目前涌現出的一系列特征檢測類的方法，最后對海雜波背景下基于特征的目標檢測技術進行展望。

2 現有的海面目標檢測方法

2.1 低分辨率短積累時間情況下的海面艦船目標檢測方法

隨著建設海洋強國戰略的確立，對海雷達裝備快速發展，后發優勢使我國完成了硬件上的“追趕超越”，形成了對海雷達“硬超越，軟滯后”的局面。對海雷達面臨共性問題：“臨界信雜比下的目標檢測問題”。低分辨警戒、預警雷達對于傳統大型艦船的檢測難度不大，通常采用非相干或者相干的檢測方法。其中，非相干類檢測方法主要是利用雷達回波的幅度和功率進行檢測，主要方法有單元平均恒虛警率(Cell-Average Constant False Alarm Rate, CA-CFAR)檢測器，最大選擇(Greatest Of,GO)或最小選擇(Smallest Of, SO) CFAR檢測器等，常用于早期非相干雷達脈沖體制的檢測中[14—16]。在相干雷達脈沖體制下，自適應類檢測算法是將海雜波建立于某種特定的統計模型下，從而發展出一系列對應于該模型的最優或近最優檢測器，檢測方法流程圖如圖3所示。

在小擦地角情況下，隨著雷達分辨率的提高，海雜波可以被建模為復高斯分布模型，基于該背景，Kelly[17]和Robey[18]分別提出了廣義似然比檢測器(Generalized Likelihood Ratio Test, GLRT)和自適應匹配濾波(Adaptive Matched Filter, AMF)檢測器，它們均具有良好的檢測效果。然而在高分辨雷達和低掠射角情況下，海雜波具有強的非高斯性，復高斯分布模型不再適用，此時可以將海雜波建模為復合高斯模型(Compound Gaussian Model,CGM)[19]，即一個慢變的紋理分量和一個快變的散斑分量的乘積

Conte[20]和Richmond等人[21]基于復合高斯模型提出了歸一化匹配濾波檢測器(N o r m a l i z e d Matched Filter, NMF)和自適應歸一化匹配濾波檢測器(Adaptive Normalized Matched Filter, ANMF)。在一個雷達相干處理時間內(Coherent Processing Interval, CPI)，復合高斯模型可以退化為球不變隨機向量模型(Spherically Invariant Random Vector, SIRV)，此時的紋理分量為正的隨機常數，散斑分量服從復高斯分布

根據紋理分量分別服從Gamma分布、逆Gamma分布和逆高斯分布的隨機變量，發展了K分布下的最優檢測器(Optimum K-distributed Detector,OKD)[22,23]，廣義Pareto功率分布下的最優廣義似然比線性門限檢測器(Generalized Likelihood Ratio Test-Linear Threshold Detector, GLRT-LTD)[24,25]和IG-CG分布下最優逆高斯紋理的廣義似然比檢測器(Generalized Likelihood Ratio Test with Inverse Gaussian texture, GLRT-IG)[26]等。此外，由于K分布下最優檢測器工程上的不可實現性，匹配于形狀參數的α-AMF檢測器[27]被提出，其結構更簡單并且檢測性能與OKD近似且工程上可實現。自適應類的檢測方法適用于短時相干累積，常用于海面上大型目標、運動目標的檢測。這類檢測器主要用于廣域的警戒雷達和監視雷達，由于要兼顧掃描效率，所以通常在一個波位駐留時間內，可積累的脈沖數有限。但是，海雜波具有較寬的多普勒帶寬，當海面目標速度較低或較小時，目標回波往往會淹沒在強的海雜波中，因此對于海面微弱目標，自適應檢測算法性能存在較大程度的下滑。因此，這類方法很難用于檢測海面的微弱目標。目標回波數據的信雜比可以利用目標所在距離單元數據的功率進行估計，首先從純雜波單元估算海雜波的平均功率 pˉc，如果假設雷達回波與海雜波是相互獨立的，那么平均信雜比可以用如式(3)進行估計

圖 3 自適應檢測方法流程圖Fig. 3 The flowchart of the adaptive detection methods

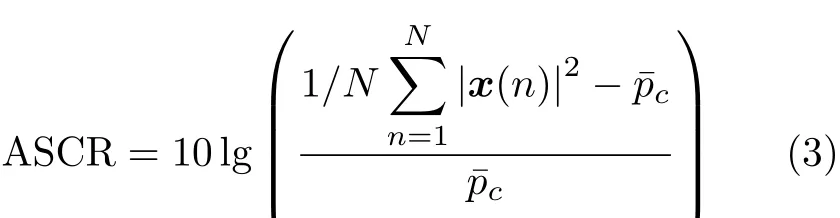
其中， x (n)表示目標所在單元回波序列，N為序列長度。實際信雜比在平均信雜比附近有一定起伏。

對于要發現隱身艦船這類小RCS目標，傳統檢測方法處于臨界信雜比狀態，需通過“認知海雜波抑制”突破困局。比如，瀕海戰斗艦的RCS約為100 m2，美國朱姆沃爾特級驅逐艦DDG1000的RCS僅為60 m2，而隱身快艇的RCS也僅為30 m2。這些隱身設計艦船的出現同樣也使得低分辨警戒雷達和預警雷達的目標檢測難度有所增加。我們通過TSC模型，仿真了VV逆風情況下，海況4級的時候針對各種不同的艦船的信雜比。從圖4可以看出，利用傳統方法，對于10脈沖最小可檢測的SCR，在50～300 km的范圍里，RCS為30 m2和60 m2的艦艇，均很難進行檢測。因此需要改變雷達工作體制和發展新型的目標檢測算法。

2.2 高距離分辨和長時間積累情況下的海面微弱目標特征檢測方法

海面目標除了大型艦船目標還包括近距離慢速小目標，由于“空間分辨率性能瓶頸”限制，如前文所述，低分辨雷達難以發現。傳統基于MTI和MTD以及自適應檢測類的目標檢測是基于精確的雜波和目標回波統計模型的，因此各種最優和近最優的檢驗統計量扮演了檢測的“主角”。隨著觀測手段的精細化，背景雜波和目標回波變得極其復雜以致難以進行精確的統計建模。在這種情況下，空間高分辨、多普勒高分辨的“雙高”體制是主要的技術途徑。目前實現雙高的雷達體制主要有如圖5所示3種情況，分別是寬發窄收模式，泛探雷達體制以及快速普查加疑似點駐留的模式。

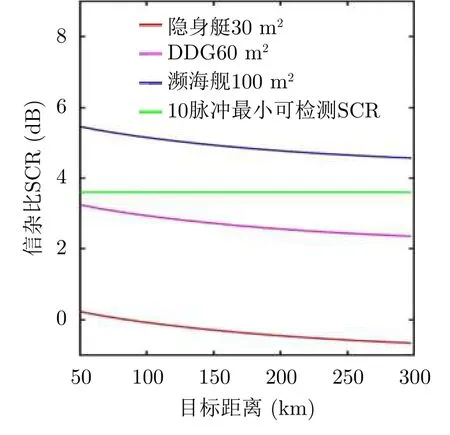
圖 4 VV極化、逆風情況下，海況4級時各種不同艦船的信雜比Fig. 4 In the case of headwind situation, SCR for various ships at sea state 4 (VV polarization)

圖 5 可實現“雙高”體制的雷達工作模式Fig. 5 Radar working modes that realize the "double high" system

高分辨小目標探測雷達需要面對極其復雜的高分辨海雜波特性和小目標回波特性，那么突破臨界信雜比檢測性能的關鍵在于：海雜波特性的深度認知(deep cognition)、精細感知(elaborate perception)和充分利用(full utilization)。這種情況下通常采用雜波和目標回波的一個或多個差異性特征實現聯合檢測，這類方法被稱為基于特征的檢測技術，簡稱為特征檢測技術。特征檢測技術在圖像處理、模式識別等領域里已經廣泛普及并產生了良好的效果，特征檢測技術可以認為是智能檢測的初步版本，是進入智能檢測時代的必經之路。海雜波背景下基于多特征的檢測方法是通過對雷達和目標回波提取具有差異性的特征，將雜波與目標高重疊的觀測空間降維到低重疊的特征空間，在特征空間中對目標進行檢測。傳統的雷達目標檢測算法都是基于某個特定的檢驗統計量，對海雜波背景下的微弱目標檢測性能有限。因此，本課題組將多特征聯合技術應用到了小目標檢測中來，提出了聯合3特征的檢測方法[28]，改善了傳統方法的性能損失問題。特征是用以描述雜波與目標之間差異性的指標，檢測中不必局限于特定的特征，而是根據實際環境和雷達的設備信息，從雷達回波的幅度、多普勒譜、時頻圖、極化信息等不同方面進行提取，由此提出基于不同特征的檢測方法。同時，隨著特征的增多，能夠更全面地反映目標和雜波的差異性，利用機器學習算法對高維特征空間進行目標檢測的方法也相繼被提出，極大程度地提高了檢測性能。作為海雜波中特征檢測問題的嘗試，國內外學者很早就開始了相關的研究，并獲得了大量的研究成果，提出了許多特征檢測類方法，如基于海面分形和混沌特征、時頻分析方法、人工智能類方法等，圖6為特征檢測方法的流程圖。下面來簡要概述一下這幾種方法，在后續的第4節有更詳細的介紹。

(1) 基于海面分形和混沌特征的檢測方法：分形理論是20世紀70年代由Mandelbrot提出的一種理論，用于表征復雜圖形和復雜過程，是非線性科學研究中一個十分活躍的分支。1993年Mcmaster大學的T. Lo等人[29]通過對實測海雜波數據的研究，根據海雜波與目標呈現出不同的分形特性，提出了一種新的基于分形理論的目標檢測方法。2006年Hu Jing等人[30]引入了基于多重分形理論的海雜波目標檢測算法，通過分析實測海雜波數據，提出海雜波數據在0.01 s到幾秒范圍內存在多重分形特征，并通過計算海雜波的Hurst指數來檢測目標，并具有良好的檢測性能。海軍航空大學的何友院士、關鍵教授、劉寧波、陳小龍等人[31,32]也在這方面做了大量的工作。基于分形的方法具有計算簡單、效率高等特點，但由于海雜波時間序列只有在一定的時間尺度的無標度區內具有分形特征，該區間隨雷達參數、海況、極化的改變而不同，且對無標度區估計出現偏差也會影響檢測器的性能。當觀測時間較長時，該類方法可以獲得對海面漂浮小目標較好的檢測性能，然而如果觀測時間較短時，檢測器的性能下滑嚴重。1995年以來，Mcmaster大學Simon Haykin教授等人[33,34]提出海雜波具有混沌特性且海雜波是短期可以預測的。根據海雜波的短期可預測性，通過對海雜波回波序列構建一個非線性預測模型，利用預測誤差進行統計假設檢驗，以達到目標檢測的目的。后來Haykin對他之前提出的海雜波混沌模型提出了質疑，且當信雜比持續降低時，檢測結果不理想，很難實現對慢速微弱小目標的檢測。

(2) 基于時頻分析的檢測方法：近些年，國內外學者提出了許多基于時頻分析的方法用來檢測海面目標[35—40]。這些方法通過時頻分析工具如短時傅里葉變換(Short-Time Fourier Transform, STFT)、Wigner-Ville分布(Wigner-Ville Distribution,WVD)、平滑偽Wigner-Ville分布(Smoothed Pesudo-Wigner-Ville Distribution, SPWVD)、分數階傅里葉變換(FRactional Fourier Transform, FRFT)等，通過參數或非參數化方法在二維平面上提取與目標對應的特征來完成海雜波背景下目標的檢測。在基于時頻分析的方法中，通過進行適當的時頻變換，可以得到更多從時域中無法得到的細節與信息，克服了傅里葉分析時域和頻域完全分離的缺點，可以兼顧時域和頻域。然而根據海森堡的測不準原理，STFT中時間窗函數的長度越長，頻率分辨率就越高，而時間分辨率則會越差。采用雙線性形式的Wigner-Ville變換可以提高時域和頻域的分辨率，但由于非線性變換，當出現多個信號成分時會出現嚴重的交叉項，交叉項的出現會降低檢測器對微弱目標的檢測性能。而SPWVD雖然可以很好地抑制交叉項，但是犧牲了算法的運算效率，并且聯合時頻分辨率也同時下降。采用FRFT的時頻分析方法雖然不存在交叉項，對大型艦船目標具有較好的檢測性能，但是對于復雜海面上慢速微弱小目標依然檢測性能不佳。海面微弱小目標由于受到海浪的影響，運動復雜，目標信號通常表現為弱的非線性調頻信號，這使得這類檢測方法在實際應用中面臨諸多挑戰。近年來，學者們對微多普勒理論的研究逐漸增多。微多普勒是由目標的微動所引起的多普勒頻移，反映了多普勒特性上的變化，目標的微動狀態能夠良好地反映目標的精細特征，因此微動目標的回波特征可以與雜波特征進行有效的區分。基于微多普勒特征的檢測方法是將微動目標的回波信號建立為合適的模型，采用傅里葉變換、時頻分布等方法對微動特征進行分析，從而提升海面微弱目標的檢測能力。現有的基于微多普勒理論的海面目標檢測方法有：基于高斯短時分數階Fourier變換的海面微動目標檢測方法[41]、基于短時稀疏時頻分布的雷達目標微動特征提取及檢測方法[42]、基于卷積神經網絡的海上微動目標檢測與分類方法[43]等。

圖 6 特征檢測流程圖Fig. 6 The flowchart of the feature-based detection methods

(3) 基于人工智能的海面目標檢測方法：基于人工智能方法的海面目標檢測開始于Haykin等人[33]提出的神經網絡類的方法，取得了一定的進展。隨著人工智能和機器學習技術的發展，一些學者們把人工智能的新技術引入到了海雜波的目標檢測中[44—48]。近年，Nerea del-Rey-Maestre和David Mata-Moya等人[49]將人工智能用于海雜波目標檢測并進行了實測數據的驗證。在他們的復合假設檢驗問題中，神經網絡檢測器可被近似成奈曼-皮爾遜準則(Neyman-Pearson, NP)檢測器。他們分析了基于約束廣義似然比(Constrained Generalized Likelihood Ratio,CGLR)的次優方法，并與基于多普勒濾波的常規方法進行了比較。其中，基于2階的神經網絡的人工智能解決方案提供了最好的結果，同時可以實時并以極低的計算成本來近似CGLR。

3 特征檢測領域常用的公開數據集介紹

3.1 IPIX數據集介紹

檢測器的性能優劣需要用實測數據進行驗證。由加拿大McMaster大學Haykin教授[50]帶領的團隊分別在1993年和1998年利用IPIX(Intelligent PIxel processing X-band)雷達采集了大量高分辨海雜波數據并公開在他們的網站上。IPIX雷達可以發射水平極化(H-polarization)和垂直極化(V-polarization)電磁波，并可以利用兩個線性接收器完成水平接收和垂直接收，因此雷達進行數據采集時通常可以得到HH, VV, HV和VH 4種極化的雷達回波數據。

這里主要介紹10組在1993年采集的數據和2組1998年采集的數據。兩次采集數據時雷達工作地點、數據采集參數和合作目標有一定區別。采集1993年數據時雷達架設在加拿大東海岸，新斯科舍省達特茅斯(Dartmouth, Nova Scotia)附近30 m高的懸崖上，雷達朝大西洋海面照射，待檢測目標是被鋁絲包裹直徑1 m的漂浮圓球。雷達工作頻率為9.3 GHz，波束寬度為0.9°，距離分辨率為30 m。雷達工作在駐留模式，脈沖重復頻率(Pulse Recurrence Frequency, PRF)為1000 Hz，駐留時間約為131 s，每組數據包含14個距離單元。由于雷達以低掠射角照射目標，目標起伏和擺動導致目標能量擴散，并且在進行數據采集時采取了距離過采樣，因此目標所在單元周圍的臨近單元會受到目標能量的影響，記為受影響單元。1993年數據的風速和浪高可以從網上數據采集時的環境記錄中獲得，數據詳情如表1所示。

根據Douglas海況標準，后9組數據為2～3海況，有少量破碎波和白帽現象的存在。由于海浪較低，目標絕大部分時間均可以被雷達波照射到；第1組數據為3～4海況，破碎波和白帽現象出現頻率增加，測試目標有時會被海浪遮住無法被雷達波直接照射。同時可以看出浪高與風速沒有直接聯系，這是由于浪高與多種因素有關，大的涌浪通常可以從浪高較高的完全發展海域傳播很遠，短時間較大的局部風通常不會對浪高造成太多的影響，但會一定程度增加破碎浪的出現頻率。

1998年IPIX雷達被安置在安大略湖(Lake Ontario)的格里姆斯比(Grimsby, Ontario)采集了一組新的數據，雷達架設高度為20 m，待測目標為漂浮的小船。距離分辨率為30 m，距離上臨界采樣，脈沖重復頻率為1000 Hz，駐留時間為60 s，包含28個距離單元。目標采集時的浪高等環境信息沒有在網上公布，數據信息如表2所示。

3.2 CSIR的Fynmeet雷達數據集介紹

CSIR雷達部署在奧弗山測試范圍(Overberg Test Range, OTB)的3號測量站(MS3)上，位置分別為南緯34°36'56.52"，東經20°17'17.46"。部署現場的平面圖如圖7所示，試驗架設位置如圖8所示。

表 1 1993年IPIX雷達數據說明[28,50]Tab. 1 The description of IPIX radar data collected in 1993[28,50]

表 2 1998年IPIX雷達數據說明[28,50]Tab. 2 The description of IPIX radar data collected in 1998[28,50]

圖 7 部署現場平面圖[11]Fig. 7 A plan overview of the deployment site[11]

圖 8 2006年試驗架設位置(OTB)[11]Fig. 8 Location of the deployment site in 2006 (OTB)[11]

表 3 OTB MS3的主要特性[11]Tab. 3 Main characteristics of OTB MS3[11]

表3顯示了部署站點雷達的主要特性。

Fynmeet動態雷達橫截面積(RCS)測量設備由CSIR開發，并由CSIR，南非軍備公司(ARMSCOR)和南非空軍(SAAF)共同擁有。從本質上講，它是經過校準的相干RCS測量設備，其工作頻率為6.5～17.5 GHz，該系統相關系統參數如表4中所示。

表 4 Fynmeet系統和性能參數[11]Tab. 4 Fynmeet system and performance specifications[11]

在試驗期間布置了以下外圍記錄設備：兩個氣象站分別以15 min和1 h的間隔記錄環境狀況，定向記錄波浪浮標以30 min為間隔記錄重要的波浪高度，最大波浪高度，波浪方向和波浪周期。

試驗期間4天采用了3艘合作船只，分別為WaveRider剛性充氣船(RIB)，Machann快艇和Timothy漁船，如圖9所示，用來記錄回波數據等測量結果。測量試驗定義了一系列海雜波和回波數據測量，包括在不同發射頻率下針對不同波形，方位角和范圍的測量。此測量試驗采用的原理是，只要環境條件發生顯著變化，就會重復進行這組測量。實際上，這組測量每天重復一次。在計劃階段，整個測量過程大約需要6.5～7.0 h，即一整天。因此試驗定義了測量的子集(例如，僅在單個頻率，單個方位角的情況下)，僅需要較少的時間來完成。最小的測量子集需要2 h完成。

圖 9 試驗合作船只[11]Fig. 9 Experimental cooperative boats[11]

試驗對海雜波成功記錄并預處理了156個測量數據集，總計超過160 min。此外，記錄了113個目標回波測量數據集(127 min)，使試驗過程中記錄的數據集總數達到269個，總記錄時間為289 min。大多數數據集都記錄了固定頻率的波形。在子集中，大多數數據集在9 GHz和6.9 GHz的發送(Tx)頻率下以15 m分辨率記錄。由于試驗期間經歷的平均風速較高，因此大多數數據集都是以165°N的天線方位角記錄的。只要有可能，就在不同的方位角(通常以15°的間隔)進行測量。定期記錄了其他頻率(8 GHz和10.3 GHz)以及其他波形的測量結果，從而可以研究不同波形和Tx頻率的海浪雜波和船回波特性之間的相關性。

3.3 海軍航空大學對海監視雷達數據集

從海雜波特性和海上目標探測技術研究需求出發，借鑒加拿大McMaster大學的IPIX雷達數據集和南非CSIR的Fynmeet雷達數據集在數據采集和記錄方面的成功經驗，海軍航空大學海上目標探測課題組推出一項“雷達對海探測數據共享計劃”，旨在利用X波段固態全相參雷達分階段分批次開展對海探測試驗，獲取多種條件下雷達實測數據和試驗輔助數據，構建形成可以用于支持海雜波特性認知、海雜波抑制、海上目標檢測跟蹤與分類識別技術研究的數據集，分批次公開共享。

試驗中所使用的雷達為X波段固態功放監視/導航雷達，主要用于船舶導航和海岸監視等場景，能清晰分辨多種量程下的各種目標，具有高距離分辨率、高可靠性、距離探測盲區小等特點，如圖10所示。雷達采用固態功放組合脈沖發射體制(見圖11)，以提高距離分辨率，減小距離盲區，降低雷達輻射功率，發射時間為40 ns～100 μs，利用接收信號和發射信號的時差計算目標距離，水平面內360°全方位掃描。雷達技術參數如表5所示。

該數據集相關的資料和數據下載鏈接可以在《雷達學報》網站上進行獲取。

3.4 其他岸基數據集介紹

圖 10 X波段固態功放監視/導航雷達[51]Fig. 10 X-band solid-state power amplifier surveillance/navigation radar[51]

圖 11 組合脈沖發射的3種模式[51]Fig. 11 Three modes of combined pulse transmission[51]

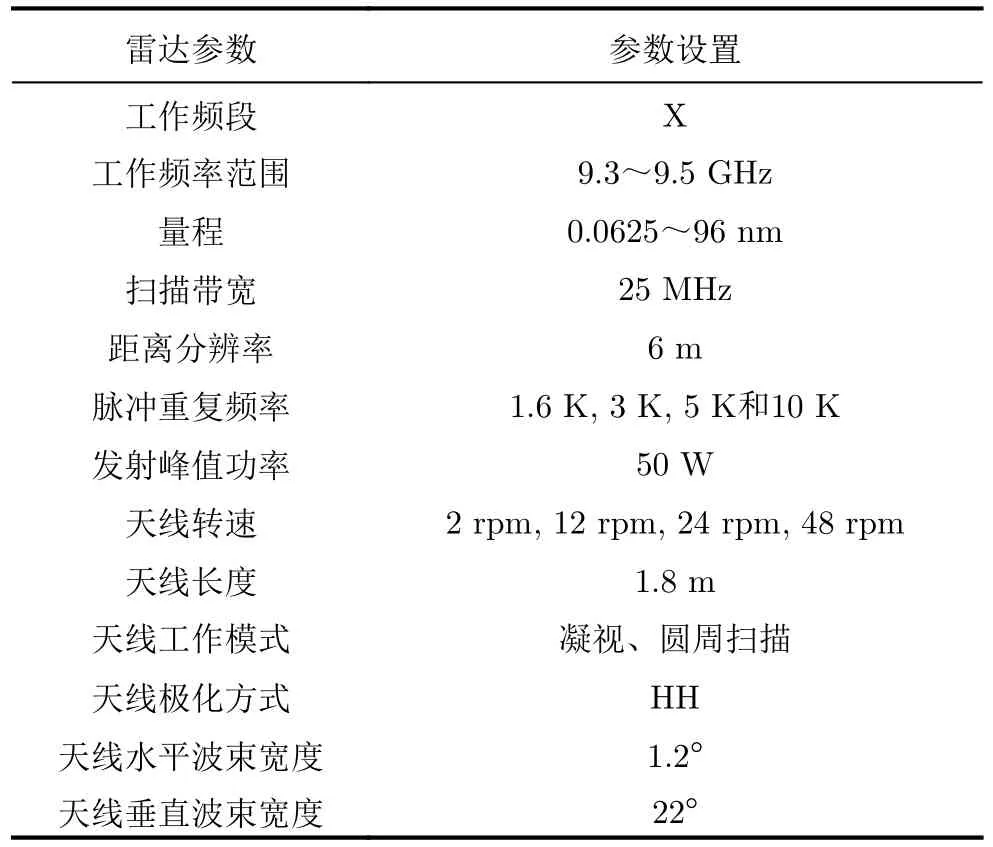
表 5 X波段試驗雷達參數[51]Tab. 5 X-band radar parameters[51]

從公開文獻來看，國外較為典型的岸基雷達海雜波測量試驗還有澳大利亞國防科技署(Defence Science and Technology Organization, DSTO)的多波段(L, S和X波段)雷達海雜波測量試驗[52—54]、美國海軍研究實驗室(Naval Research Laboratory,NRL)的X波段雷達海雜波測量試驗[55]、西班牙南海岸Ka波段高分辨率雷達海雜波測量試驗[56]等。除此之外，還包括美國海軍空戰中心的多波段(UHF,L, S, C, X和Ku波段)雷達小擦地角海雜波測量試驗[57,58]、英格蘭南海岸多波段(S, X和Ku波段)雷達海雜波測量試驗[59]、日本的X波段雷達海雜波測量試驗[60]、德國和法國聯合開展的MARLENE(Mediterranean RFC and Sea Clutter Environmental Experiment)多波段(C, X, Ku, Ka和W波段)雷達海雜波測量試驗[61]、倫敦大學(University College London, UCL)的S波段NetRAD單/雙基地雷達海雜波測量試驗[62—66]等。

4 基于特征的檢測方法的研究進展

如前文所述，隨著觀測手段的精細化，背景雜波和目標回波變得極其復雜以致難以進行精確的統計建模。在這種情況下，空間高分辨、多普勒高分辨的“雙高”體制是主要的技術途徑。而高分辨小目標探測雷達需要面對極其復雜的高分辨海雜波特性和小目標回波特性，那么突破臨界信雜比檢測性能的關鍵在于：海雜波特性的深度認知、精細感知和充分利用。本節將著重介紹基于高距離分辨和長時間觀測雷達體制下的基于特征的檢測器的發展歷程和動態。需要說明的是，本文中主要涉及信號層面的特征，沒有涉及航跡和數據層面的特征，因此對數據級層面的特征將不進行介紹。

基于特征的檢測方法現有的特征列表如表6。分形特征是早期特征檢測采用的單一特征，在長時觀測下對海面漂浮小目標有良好的檢測效果[29,31,67]，隨后，大量學者研究了多重分形特征[30,68]、不同變換域上的分形特征[69—73]并取得良好的檢測結果；海雜波的混沌特征認為海雜波時間序列可以利用某種非線性動態模型來描述其演化規律并進行預測[33]，利用預測誤差來進行判斷。基于海雜波的復合高斯模型，為了消除長時觀測下復合高斯模型中紋理分量非平穩性的影響，提出了散斑一致性因子特征[74]，它也屬于時域特征的一種。單一特征檢測均利用所計算的特征值與給定虛警概率下的門限進行比較，從而判斷目標的有無。隨著特征檢測方法的發展，大量不同層面的特征被提出，基于時域能量和頻譜差異的特征[28]，基于時頻分析的適用于微動目標的微多普勒特征[41,42]和基于海雜波歸一化時頻分布差異的特征[75]，以及極化特征[76]。表6給出了常用的幾種特征。隨著特征數目的增多，單一特征檢測會造成一定的性能損失，聯合多特征進行檢測是大勢所趨。然而，聯合多特征檢測中如何確定檢測器門限成為了多特征檢測的難題。本課題組在文獻[28]提出了凸包學習算法，將檢測問題視為單分類問題，檢測門限的確定轉化為檢測判決區域的選取，然而其具有一定的局限性，僅適合三維特征空間的檢測，隨著維數的增加，凸包學習算法的復雜度提高，難以進行檢測。隨后，基于機器學習的算法被提出，文獻[77,78]分別利用支撐向量機和決策樹算法選取判決區域，突破了維數的限制，可有效利用多維特征進行檢測，并可以取得良好的檢測結果。下面對幾種特征及檢測方法進行詳細的介紹。

表 6 現有特征檢測方法的特征Tab. 6 Features introduction of feature-based detection method

4.1 基于分形特征的海面小目標檢測方法

受檢測器設計的維度限制，早期的海面小目標檢測方法以單特征檢測為主，單特征檢測器由于檢測器設計簡單和檢測器門限易于確定，所以一直以來受到學者們的關注。國內外學者基于不同的方法，在不同的表示域，提出了很多有效的特征檢測方法。

分形(fractal)理論是20世紀70年代由Mandelbrot提出的一種理論，它用來描述傳統歐幾里德幾何學無法分析的不規則自然特征，大到山川、閃電、海岸線、宇宙星系，小到雪花、冰晶、樹葉等大自然形成的圖形和復雜過程，是非線性科學研究中一個十分活躍的分支[79,80]。分形可以描述大自然中從宏觀到微觀不同尺度具有一定自相似性的現象或物質。海面本身波浪起伏，大尺度的涌浪攜帶著不同波長海浪同樣具有一定的分形特性。D. L. Jaggard等人[81,82]經過對具有分形特性的粗糙表面的光和電磁波反射回波的分析發現，回波同樣具有一定的分形特性。G. Franceschetti等人[83]進一步將從自然粗糙表面反射的電磁回波描述為二維分形布朗運動。F. Berizzi等人[84]經過對海面以及海雜波的分析，進一步提出海雜波在一定程度上滿足分形特性，并具有與海面近似相同的分形維數。在此基礎上，F. Berizzi等人[85]利用分形的方法生成海雜波，該方法可以描述雜波與海態、雷達等的關系，克服了傳統利用統計模型的方法生成海雜波與操作條件和環境無關的缺點，同時將海雜波的分形特性保留在生成的雜波中。

1993年T. Lo等人[29]對實測海雜波數據研究發現，海雜波的分形維數大約是1.75，而當海雜波中存在目標信號時，海面原本的分形程度降低了，由此在分形理論的基礎上提出了一種新的目標檢測方法。分形布朗運動(Fractional Brownian Motion,FBM)是最簡單的單分形模型。因為分形布朗運動經過傅里葉變換后依然具有分形特征，有學者在將海雜波幅度回波序列建模為分形布朗運動的基礎上，對實測海雜波頻譜的分形特性進行了研究，并對檢測海面目標進行了嘗試[31,67]。2002年Gao等人[68]分析了海雜波的幅度分布、時空相關等特性，并從理論上證明了實測海雜波數據是多重分形的。2006年Hu Jing等人[30]引入了基于多重分形理論的海雜波目標檢測算法，通過分析實測海雜波數據，提出海雜波數據在0.01 s到幾秒范圍內存在多重分形特征，通過計算海雜波的Hurst指數，提出的目標檢測算法具有良好的檢測性能。檢測方法如下：

(4) 當H(q)不隨q的變化而變化時，序列即為單分形，否則認為是多分形序列。當q=2時，通常稱為Hurst指數，通過比較Hurst指數的大小，基于Hurst指數構建基于分形的檢測器。

(5) 設定門限，如果序列Hurst指數大于門限時，即可判斷有目標存在。

圖 12 14個距離單元分形特性分析[30]Fig. 12 Analysis of fractal characteristics in 14 range cells[30]

可以通過實測海雜波數據驗證該檢測器的檢測性能。當q=2時，如圖12所示。實心線代表純海雜波距離單元回波數據，空心線為目標單元及目標單元周圍的影響距離單元回波數據。從圖12(a)中可以看出從24～212區間也就是0.08～4.00 s近似為線性，可以認為在該區間內海雜波數據具有分形結構，被稱為無標度區。用最小二乘法對無標度區曲線進行擬合，求得直線的斜率H(2)，即Hurst指數，所得結果如圖12(b)所示，可以看出目標單元及其周圍影響單元的Hurst指數明顯高于純雜波單元。因此利用Hurst指數可以完成對海面目標的檢測。

下面檢驗該實測海雜波數據是否為多分形結構，H(q)與q的關系圖如圖13所示，同樣，實心線代表純雜波單元，空心線代表目標單元及影響單元。可以看到H(q)是q的函數，由此可得海雜波數據具有多分形特征，特別是回波中含有目標時，H(q)隨q的變換更劇烈。

利用Hurst指數構建的目標檢測器，在對IPIX雷達93年10組HH極化下海雜波數據的檢測結果如圖14。

實心代表目標單元，空心代表純雜波單元，可以看到檢測結果非常理想。實驗數據HH極化下純雜波單元與目標單元Hurst指數可以完全分開。該種方法在其他極化下的檢測效果也較為理想。但由于93年數據每個距離單元觀測時間較長約為131 s，該種方法隨著觀測時間的縮短，檢測性能下降很快。

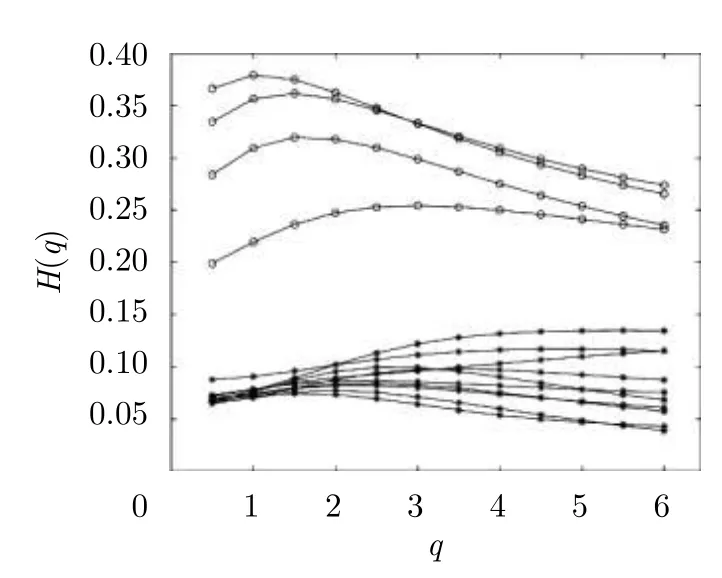
圖 13 14個距離單元H(q)趨勢圖[30]Fig. 13 The trends of H(q) in 14 range cells[30]

學者們也將時域的非線性分形特征檢測器推廣到其他的變換域。分數階傅里葉變換域(FRFT)的分形特性也是學者們研究的熱點。文獻[69,70]對海雜波FRFT譜的多重分形特性進行了研究，并在實測數據上進行了驗證。文獻[71]提出了一種基于FRFT域空間分形特征差異的海面弱目標檢測方法，提高了海雜波背景下弱目標的檢測性能。文獻[72]基于海雜波FRFT譜計算了多尺度Hurst指數，相較于傳統多尺度Hurst指數，有效提升了目標檢測性能。近些年，南京郵電大學團隊提出了一種FRFT域分形特征檢測器[73]，主要基于FRFT域的分形特征進行分析海雜波與漂浮小目標的差異性特征，通過去趨勢波動分析法，得到目標與海雜波的分形曲線，選取適合的尺度不變區間提取分形維和分形維方差，通過凸包判決完成兩特征的聯合檢測分析，并與單特征檢測和均值類CFAR檢測器性能對比，驗證所提算法的有效性。

圖15為FRFT域分形特征檢測器的原理框圖。通過對海雜波與目標在FRFT域的分形維和分形維方差進行了研究，圖16為去趨勢波動分析法確定的分形曲線，通過尺度不變區間的選取得到分形維和分形維方差兩組特征，圖17為虛警為10—3和10—2時訓練樣本和待分類樣本的平面示意圖。圖18為FRFT域兩特征聯合檢測器與均值類CFAR檢測器的性能對比圖。

圖 14 HH極化下純雜波單元與含目標單元Hurst頻率分布圖[30]Fig. 14 Hurst frequency distribution of clutter cells and target cells under HH polarization[30]

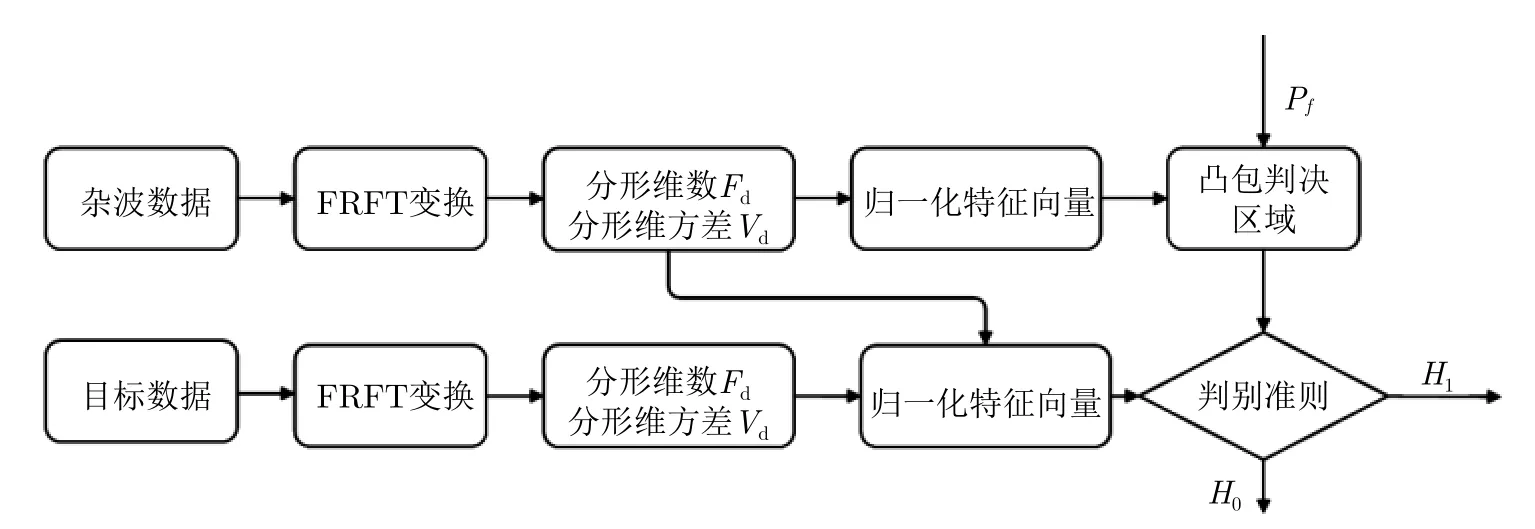
圖 15 分形特征檢測器的原理框圖[73]Fig. 15 The flowchart of fractal-based detector[73]

圖 16 分形曲線[73]Fig. 16 Fractal curves[73]

基于海雜波的分形特性，近些年衍生出了一系列基于分形理論的檢測算法，包括單分形特征、多重分形特征[86,87]、多重分形關聯譜[88]、高階分形特征、擴展自相似特性、模糊分形理論等。隨著分形理論的發展，越來越多的檢測方法不斷出現，成為目標檢測方向的研究熱門。

4.2 基于海雜波混沌特征的檢測方法

圖 17 訓練樣本和待分類樣本在二維特征平面的顯示圖[73]Fig. 17 The distribution of training samples and test samples on the two-dimensional feature plane[73]

海面是一個非常復雜的動力學系統，由此得到的海面雷達回波受到風向、浪高、浪向、洋流等因素的影響，海雜波回波序列具有明顯的非線性特性。1995年，Haykin教授等人[33]運用了關聯維、Lyapunov指數以及Kolmogorov熵3個指標，并指出，海雜波具有有限相關維數；其最大Lyapunov指數為正；海雜波是短期可以預測的。其中，相關維數和最大Lyapunov指數對于構成時間序列的雷達信號分量都是必不可少的，并且不會隨海況或地理位置發生顯著變化。這些結果表明，可能存在導致海雜波產生的普遍混沌結構，從而確定了海雜波時間序列具有明顯的混沌特性。根據海雜波的短期可預測性，通過對海雜波回波序列構建一個非線性預測模型，利用預測誤差進行統計假設檢驗，以達到目標檢測目的[89—93]。基于混沌理論模型認為海雜波時間序列可以利用某種非線性動態模型來描述其演化規律并進行預測，因此利用神經網絡學習方法可以對海雜波序列完成非線性擬合，通過預測誤差完成目標檢測。混沌系統對噪聲異常敏感，具有明顯的“蝴蝶效應”，然而實際系統中不可避免地受到各種噪聲的影響[94]，進而引起系統的異常和不穩定。海雜波混沌模型在學術界一度引起了爭議，后來Haykin對之前提出的海雜波混沌模型提出了修正，認為海雜波本質上可能由隨機混沌或多個確定性混沌或兩者混合產生，而越來越多的學者指出海雜波不具有混沌特性[95—97]。但是這種基于神經網絡以及支撐矢量機(Support Vector Machine, SVM)等預測器提供的異常檢測思想成為了特征檢測研究的一條思路。基于海雜波混沌模型建立起的檢測算法的主體思想如圖19所示。

xA(n)是 實際接收到的信號，基于神經網絡算法所得到的預測信號。當 xA(n)只包含海面回波，輸出預測誤差 e (n)較 小；但當 xA(n)中包含目標回波時，輸出 e (n)會有一個較大的值。基于此可以得到基于混沌模型的目標檢測算法如下：

(1) 對于一個回波信號xA(n)， 其中 n =1,2,··,NT，通過神經網絡模型得到預測算預測誤

(2) 在觀測時間內計算累計預測均方誤差得到

圖 18 經典CFAR算法檢測曲線[73]Fig. 18 Classic CFAR algorithm detection curves[73]

圖 19 基于神經網絡預測的檢測器框圖[33]Fig. 19 The flowchart of detector based on neural network prediction[33]

其中 NT為觀測時間內信號長度。

(3) 將 Ee與給定虛警概率的門限進行比較，如果超過門限，認為存在目標H1假設成立；否則認為沒有目標H0假設成立。

圖20為檢測結果ROC曲線，實線為傳統多普勒恒虛警檢測算法，虛線為基于神經網絡的恒虛警檢測算法，可以看出基于神經網絡算法的檢測性能優于傳統多普勒算法。

基于神經網絡的檢測方法通過對海雜波時間序列的學習，能夠對海雜波序列進行良好的擬合，從而通過預測海雜波時間序列，利用預測誤差對目標進行檢測。其檢測框圖如圖21所示。神經網絡對海雜波時間序列的學習規則，可以理解為用神經網絡建立了復雜的非線性映射，海雜波的所有特征都是神經網絡的學習對象，因此基于該網絡預測誤差的檢測方法是基于海雜波全特征的檢測方法。然而基于全特征的檢測方法具有較多的缺點，由于海雜波與目標的共性特征比差異性特征多且貢獻少，擠占了大量神經網絡的資源，增加了網絡的學習規模并降低了學習效率，其規模過大的網絡使得學習過程訓練過多的精細特征，產生“過擬合”現象，網絡的泛化能力較差。因此，基于神經網絡的學習在很長一段時間受到研究人員的冷落。

圖 20 基于神經網絡檢測器和傳統多普勒CFAR檢測器的ROC曲線[33]Fig. 20 ROC curves of the detector based on neural network and traditional Doppler CFAR detector[33]

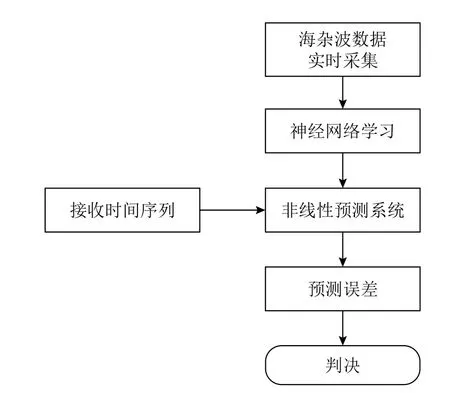
圖 21 基于預測的檢測方法流程圖Fig. 21 The flowchart of detection methods based on prediction

然而，隨著深度學習和人工智能的發展，基于神經網絡的學習方法在雷達目標檢測中產生了良好的應用[98]。典型的深度學習網絡有卷積神經網絡(Convolutional Neural Network, CNN)、稀疏自編碼器(Sparse AutoEncoder, SAE)、深度置信網絡(Deep Belief Network, DBN)等等，它們均在合成孔徑雷達(Synthetic Aperture Radar, SAR)圖像中展開了廣泛的應用并且產生了良好的結果，其中，CNN的應用最為廣泛。CNN主要包含卷積層、池化層和全連接層，卷積層提取輸入圖像低級到復雜的特征，池化層對于該圖像進行下采樣處理，從而減少特征，一定程度上控制過擬合，全連接層將上一層所得到的特征進行排列，對其進行神經網絡的連接。SAE方法能夠在無監督情況下提取特征，因此成為人們研究的重點。將CNN與SAE結合起來可以得到卷積自編碼器(Convolutional Automatic Encoder, CAE)，在實際應用中也可以產生良好的效果。深度學習網絡的出現為海面目標檢測引領了新的方向，基于海面目標的微動特征，有學者提出了利用CNN對海面目標的微多普勒譜圖進行分析和處理，相較于傳統方法產生了良好的結果[43]，越來越多的學者也在嘗試利用深度學習網絡對海面目標進行檢測和分類，神經網絡在海面目標檢測中的應用還在不斷發展和擴大。

4.3 基于微多普勒特征的海面目標檢測方法

現代雷達為了提高距離高分辨率和探測距離，通常發射信號選用大時寬帶寬積信號，線性調頻信號(Linear Frequency Modulation, LFM)模擬和數字產生均比較方便，形式簡單，因此對其的研究也較為深入。時頻分析方法能提供較好的時域和頻域聯合分布信息，在信號處理領域得到了廣泛應用，成為了分析時變非平穩信號的有力工具。當目標相對于雷達進行勻加速或勻減速運動時，由于多普勒效應，目標回波為線性調頻信號，國內外學者利用時頻分析工具如短時傅里葉變化、分數階傅里葉變換(FRFT), Wigner-Hough變換，偽維格納-威利分布(Pesudo-Wigner-Ville Distribution, PWVD),Radon-Wigner變換[99,100], Radon-ambiguity變換[101],Chirplet transform[102]等，通過參數與非參數方法完成對非平穩背景下線性調頻信號的檢測[103]。

根據SAR圖像中艦船尾跡的特性，Radon變換和Hough變換被應用于對海面艦船的檢測[104,105]，這類方法需要完成對觀測區域的成像，檢測性能的好壞與成像品質關系密切。針對海雜波的非均勻非平穩特性，國內外學者提出了許多基于時頻分布的檢測方法用來檢測目標[106—111]。海雜波和目標在時頻聚集性和持續時間上具有一定差異，基于此，有學者通過對時頻迭代分解算法進行目標檢測[112,113]。分數階傅里葉變化可以看作對時頻平面的旋轉操作，且沒有交叉項困擾，十分適合處理線性調頻信號，國內有學者將分數階傅里葉變化應用在海面勻加速目標檢測中[114—116]。然而海面目標通常會受到海浪的影響，目標信號表現為非線性調頻信號，這使得此類檢測方法在實際應用中檢測性能存在一定的下滑。為了提高對海面目標的檢測性能，近年來，中外學者通過時頻分析提出了新的檢測方法[35—40]。Haykin在文獻[35]中通過將海面背景下目標檢測問題轉換為模式識別中的雙分類問題，利用主成分分析法(Principal Component Analysis, PCA)從時頻平面中提取時頻特征，通過神經網絡算法完成雜波與目標的分類。然而實際中雷達需要對未知目標進行探測，因此目標的特征是無法確切獲得的，限制了該方法在實際當中的應用，但這種將目標檢測問題轉化為雙分類問題的思想給海面漂浮小目標的檢測提供了一個新的思路。小波變換以其優秀的時頻局部特性，可以觀測到雷達回波中不同的細節信息，因此也有學者嘗試用小波變換檢測海面中的目標[117]。近些年，很多學者基于微多普勒理論以及基于雷達回波時頻圖的深度神經網絡目標檢測方法，也屬于時頻分析類方法的范疇。

微多普勒理論是近年來目標探測領域的熱點，通過對微動目標的回波進行分析和建模，提取目標的微動特征并利用不同的檢測方法對其進行檢測。將微多普勒理論引入海面微弱目標檢測中，產生了良好的檢測結果。海軍航空大學團隊基于微多普勒理論提出了基于高斯短時分數階Fourier變換的海面微動目標檢測方法[41]、基于短時稀疏時頻分布的雷達目標微動特征提取及檢測方法[42]、基于卷積神經網絡的海上微動目標檢測與分類方法[43]等。

(1) 基于高斯短時分數階Fourier變換的海面微動目標檢測方法[41]。文獻[118]介紹了海面剛體目標微動特征的建模，并分別對短時觀測條件下和長時觀測條件下的微動目標模型進行了研究。海面目標的運動是在三維空間中的復合運動，其微動特征可以表現為目標平動中的非勻速運動以及3軸轉動，文獻[41]應用了短時觀測的條件下海面微動目標的模型，將其建模為幅度起伏的調頻信號，同一距離單元內海面微動目標回波可以建模為其中， Ai(t)表 示第i個微動信號的幅度， fi為中心頻率， ki為調頻率。在高海情狀態下，海尖峰呈現微多普勒特性，雷達常會將海尖峰誤判為目標信號，因此，研究微動目標之前采用Fred Posner等人[119]提出的基于3特征參數的海尖峰識別方法對海尖峰進行抑制。對提取出海尖峰的海雜波時間序列采用基于高斯窗函數的STFR-FT(Gaussian STFRFT,GSTFRFT)方法進行運算，通過將變換后的幅值作為檢驗統計量并與給定虛警概率下的檢測門限進行比較，判斷有無目標。圖22為海雜波抑制后的微動信號變換域特征，圖23為海雜波抑制后基于STFT和GSTFRFT的微動信號檢測結果比較。在GSTFRFT域中，微動信號的能量得到積累，峰值較為尖銳且旁瓣較低，由于對海尖峰的抑制，對SCR進行了改善，從而提升了檢測概率，相較于經典MTD算法，GSTFRFT檢測方法可以提升30%以上的檢測性能。

(2) 基于短時稀疏時頻分布的雷達目標微動特征提取及檢測方法[42]。文獻[42]采用式(6)表示的微動信號，選取了幾種常用的時頻分布對海面微動信號進行分析，即短時傅里葉變換(STFT)、Wigner-Vill分布(WVD)、平滑的偽Wigner-Vill分布(Smoothed Pseudo WVD, SPWVD)及分數階傅里葉變換(FRFT)，其中，STFT技術的時頻分辨力較差，WVD具有嚴重的交叉項，SPWVD難以突出微動信號的高分辨瞬時調頻特性，而FRFT作為參數搜索類方法，參數的估計精度會受到時頻分辨力等因素的限制。針對微動信號與海雜波稀疏性的不同，可以利用稀疏分解的思想，將稀疏時頻分布(STFD)引入海面目標檢測，提出了兩種短時稀疏時頻分布(ST-SFTD)的微動特征提取和檢測方法，分別為短時稀疏傅里葉變換(ST-SFT)和短時稀疏分數階傅里葉變換(ST-SFRFT)。圖24和圖25分別為基于ST-SFT的海上微動目標檢測結果和基于ST-SFRFT的海上微動目標檢測結果。表7為不同方法海上微動目標檢測性能對比結果。通過比較傳統的TFD方法和ST-STFD方法，由于ST-STFD方法在微動信號的最優稀疏域設計檢測算法，其檢測性能明顯提高，然而ST-STFD方法的計算效率仍有待提高。

(3) 基于CNN的海上微動目標檢測與分類方法[43]。隨著深度學習的迅速發展，更多的智能化手段應用到了海面目標檢測中。基于目標微動特征的時變性，可以利用時頻圖對微動目標進行有效的分析。文獻[43]通過CNN對雷達回波時頻圖進行了檢測和分類，并產生了良好的檢測結果。常用的卷積神經網絡有LeNet, AlexNet和GoogLeNet, LeNet是最早用于數字識別的卷積神經網絡；AlexNet比LeNet層次更深，能夠對更復雜的對象進行學習；而GoogLeNet增加了神經網絡的深度和寬度，并且保證了計算資源的不變。文獻[43]中目標檢測的訓練集和測試集均分為雜波和目標兩類，實測海雜波數據短時傅里葉變換后得到的時頻圖作為雜波訓練集和測試集，通過海面微動目標建模按照一定的信雜比仿真的目標信號作為目標訓練集和測試集，首先利用訓練集對CNN模型進行訓練，之后利用3種CNN模型對測試集進行了檢測，3種CNN模型對信號處理效率相當，其中LeNet模型檢測概率最高，而AlexNet模型的虛警概率更低。圖26為基于CNN的檢測方法流程圖，其檢測結果如表8所示。相較于傳統的SVM方法對目標時頻圖進行分類和檢測，基于CNN的檢測方法具有更高的檢測概率和更低的虛警率，但后者容易受到信雜比的影響。

圖 22 海雜波抑制后的微動信號變換域特征(N=256)[41]Fig. 22 Micro-motion signal features after sea clutter suppression (N=256)[41]

圖 23 海雜波抑制后基于STFT和GSTFRFT的微動信號檢測結果比較(N=512)[41]Fig. 23 Comparison of micro-motion target detection results based on STFT and GSTFRFT after sea clutter suppression (N=512)[41]

圖 24 基于ST-SFT的海上微動目標檢測結果(起始時間=20 s)[42]Fig. 24 ST-SFT-based micro-motion targets detection results (starting time=20 s)[42]

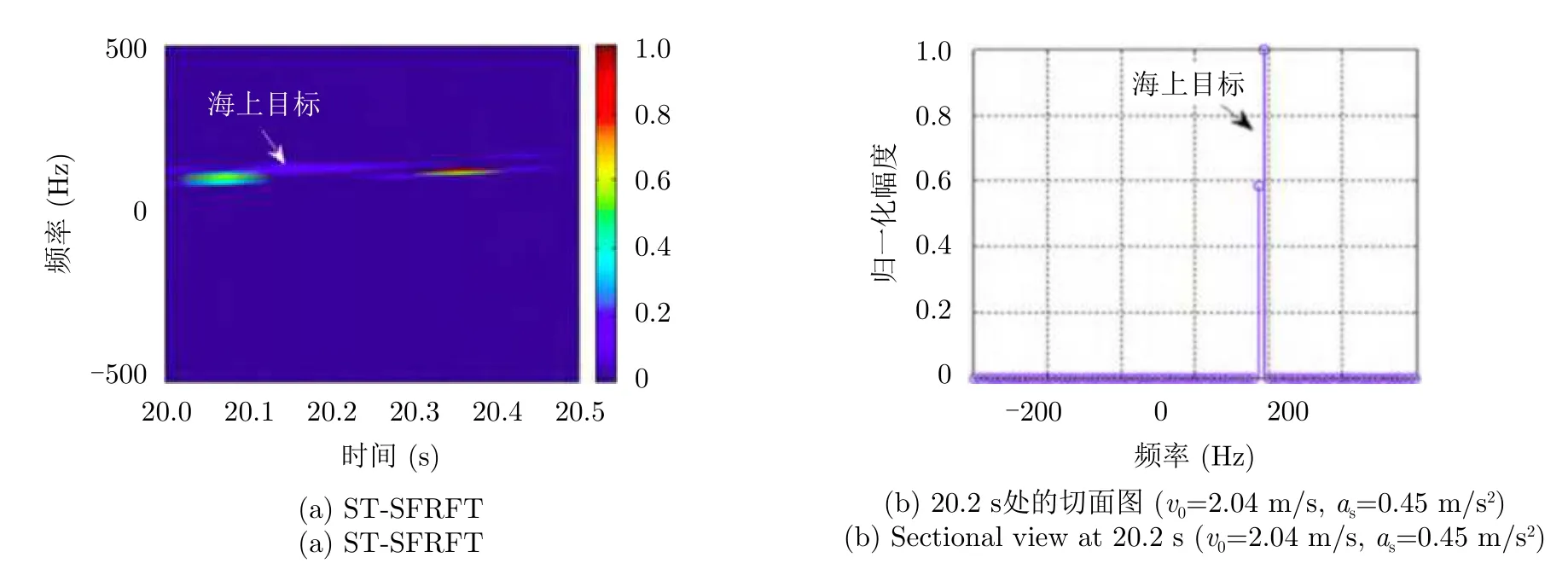
圖 25 基于ST-SFRFT的海上微動目標檢測結果(起始時間=20 s)[42]Fig. 25 ST-SFRFT-based micro-motion targets detection results (starting time=20 s)[42]

表 7 不同方法海上微動目標檢測性能對比[42]Tab. 7 Detection performance of different methods of micro-motion model of maritime targets[42]

4.4 基于散斑一致性因子特征的檢測算法

近些年，基于雜波和目標的特征差異，有學者提出了利用散斑平穩性作為特征差異在海雜波中檢測目標[74]。海雜波具有非平穩特性，具體體現在海雜波的紋理是非平穩的，海雜波的散斑在一定時間內是近似平穩的。紋理的非平穩對海面目標檢測不利，需要先進行去除，因此該方法首先從非平穩的海雜波中提取出散斑，之后基于散斑的特性來設計檢測統計量。由于海面漂浮小目標具有較強的結構性，而散斑的結構特性沒有海面漂浮小目標明顯，即隨著時間的推移，海雜波散斑的一致性要弱于目標的一致性。結合上述兩個物理依據，提出了散斑的一致性作為特征對海面漂浮小目標進行檢測，其檢測流程如圖27所示。

首先，利用參考樣本 rq,k進行歸一化樣本協方差矩陣(Normalized Samples Covariance Matrix,NSCM)估計，得到NSCM估計值 Mq，其中q為時間間隔，K為參考單元數目，N為積累脈沖個數

式(8)對式(7)結果進行標準化處理，得到 Mq,tr(·)表示求矩陣的跡

圖 26 基于CNN的檢測方法流程圖[43]Fig. 26 Processing flow diagram of method based on CNN[43]

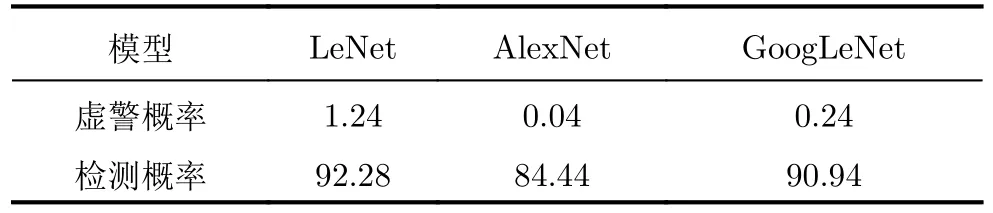
表 8 不同模型目標檢測結果(%)[43]Tab. 8 The detection results of different models(%)[43]

圖 27 散斑的平均一致性因子檢測器的流程圖[74]Fig. 27 The flowchart of a feature-based detector using the average consistency factor of speckle[74]

然后，利用歸一化值 Mˉq按照式(9)計算散斑的一致性因子, τ為時間間隔，‖ · ‖2為矩陣的2-范數

最后對散斑的一致性因子進行均值處理，得到散斑的平均一致性因子

其中[ τ1,τ2]為平均時間間隔。散斑的一致性體現了散斑的協方差矩陣在時間上的相似程度，進一步可以反映為散斑的結構平穩性。平均一致性因子越小，說明散斑在時間上的平穩性越強。漂浮小目標結構性強于海雜波的結構性，所以含有漂浮小目標的數據其散斑的平均一致性因子會小于純海雜波的散斑的一致性因子。

圖28為4種極化下散斑一致性因子的分布圖，圖29為利用散斑一致性因子特征檢測器在實測數據中的性能對比。

4.5 基于多特征融合的海面目標檢測技術

隨著雷達分辨率的進一步提高和駐留時間的增長，很多新的信號處理方法得以應用，這樣就產生了多種可以有效檢測目標的特征，而多個特征之間對于不同類型的目標會產生互補作用，能極大地提升檢測器的魯棒性。隨著新的多特征檢測器的成功設計和信號處理硬件水平的逐步提升，目前基于特征工程的多特征檢測方法以及基于人工智能自主選擇多特征的檢測方法越來越成熟，成為了海面目標特征檢測的一個重要的研究方向。

4.5.1 基于時域、頻域3特征的檢測方法

在特征檢測中，特征的提取至關重要。特征區分目標和雜波的能力很大程度上決定了檢測器的性能。特征的提取可以從提取目標和雜波具有差異性的數字特征，借鑒傳統雷達目標檢測中使用的傳統檢驗統計量，通過對目標回波特性的全面認知，按照認知結論幫助選擇差異性特征。假設雷達在一個波位發射長度為N的相干脈沖串，通過I/Q通道接收，可以得到每個距離單元的復回波數據。那么雷達目標檢測問題可以表述成如式(11)二元假設問題

圖 28 4種極化下純雜波和目標雜波的平均一致性因子[74]Fig. 28 The average consistency factors of pure clutter and clutter with target under 4 polarization channels[74]

其中，x(n)表示待檢測單元CUT的接收時間序列，s(n)表示來自目標的時間序列，c(n)表示接收的海雜波時間序列，N是脈沖累積數目，P是CUT周圍的參考單元的數目。H0假設表示雷達回波僅包含海雜波和噪聲，H1假設表示雷達回波中包含目標。從接收的雷達回波中可以得到大量的純雜波數據，從而能夠提取到純雜波的特征向量 ξi，這些特征向量可以構成純雜波模式的訓練樣本LH0={ξi∈ R3:i=1,2,··,I}。當接收到的雷達回波中包含目標時，由于海面目標的復雜性和多樣性，難以獲取各類目標的回波以及特征向量，無法獲得足夠的訓練樣本。因此，可以利用純雜波模式下的訓練樣本訓練得到判決區域，通過判斷待檢測單元回波的特征向量是否落入判決區域來判斷目標是否存在，若落入判決區域，則目標存在；若沒有落入判決區域，則目標不存在。

(1) 基于原始3特征的檢測方法[28]。盡管分形特征在長時間觀測的情況下具有良好的檢測性能，然而在實際海面目標檢測中，觀測條件無法達到理想的長時觀測，無法在實際應用中達到理想的效果。為了改善基于分形特征檢測器的問題，漂浮小目標的聯合3特征檢測方法[28]被提出，其主要思想是利用區分目標和雜波具有互補特性的3類特征對海面漂浮小目標進行檢測，將檢測問題轉化為特征空間中的單分類問題，隨后利用快速凸包學習算法確定判決區域，從而進行目標檢測。

在雷達回波中，分別從時域和頻域提取具有可分性的3種特征，時域的能量信息可以作為區分目標和雜波的標志，利用頻譜的差異性也可以對目標和雜波進行區分，由此可以提取出相對平均幅度(Relative Average Amplitude, RAA)、相對多普勒峰高(Relative doppler Peak Height, RPH)和相對多普勒譜熵(Relative Vector-Entropy, RVE)。圖30為一組雷達數據的三維特征空間分布情況，觀測時間分別為0.512 s, 1.024 s, 2.048 s和4.096 s。隨著觀測時間的增加，目標與雜波的分離性越好，檢測性能越好。

圖 29 L=1024, 4種極化下4種檢測器的檢測概率[74]Fig. 29 L = 1024, the detection probabilities of the four detectors under 4 polarization channels[74]

圖 30 純雜波與目標在特征空間中的分布情況Fig. 30 Distributions of features of clutter-only vectors and vectors with target in 3D feature space

快速凸包學習算法將給定虛警率下最優檢測判決區域簡化為如式(12)的凸包區域

其中， # A 代 表集合A的元素個數， PF為虛警概率，I為純雜波特征向量總數。圖31示意了原始的純雜波數據生成的凸包和給定虛警概率下縮小的凸包。

基于3特征的檢測器檢測步驟分為訓練和檢測兩部分。在訓練部分，需要采集雜波樣本，提取純雜波特征，然后利用快速凸包學習算法訓練出滿足虛警條件的檢測判決區域，如圖31；在檢測部分，需要對待檢測樣本進行采集，提取該樣本特征，通過判斷樣本特征是否落在判決區域內判斷待檢測單元是否存在目標。

(2) 基于SVM的特征檢測方法[77]。隨著特征檢測的發展，越來越多有效特征被用于區分海雜波和目標回波。通過有效特征的提取，可以將在海雜波中的目標檢測問題轉化為特征空間的一種特殊二分類問題。眾所周知，機器學習算法中有很多優異的算法可以很好地實現二分類問題，比如支撐矢量機(Support Vector Machine, SVM)、神經網絡(Neural Network, NN)等等。但是，由于傳統機器學習算法的核心在于搜索一個可以使得兩類錯誤率均衡且最小的分類面，但是在雷達目標檢測中對虛警概率的要求遠遠高于漏檢概率(通常，漏檢概率可達十分之幾，但是虛警概率一般低于10—3)。所以，結合機器學習算法和目標檢測問題的核心在于，如何準確的控制虛警概率。2019年，Li等人通過將SVM和雷達目標檢測問題結合起來，構建了一種基于SVM的特征檢測方法，其不僅實現了可控虛警，更與其余檢測器相比具有更優秀的檢測性能。

首先從接收海雜波序列中提取了3類特征，即時域的信息熵(Temporal Information Entropy,TIE)，時域的Hurst指數(Temporal Hurst Exponent,THE)和頻譜峰值與均值之比(Frequency Peak to Average Ratio, FPAR)，并通過它們建立了一個三維的特征向量 Fi， 用 yi={+1, —1}分別標記目標(+1)和海雜波(—1)，那么M個訓練樣本標記后可以表示成 { (Fi,yi),i=1,2,··,M}。在此特征空間中，目標和雜波的特征向量是線性不可分的。為了解決該問題，可以利用非線性核函數將三維特征向量Fi映射到高維的特征空間，可將線性不可分的數據轉換成線性可分的數據，在此，可以將徑向基函數作為核函數構建SVM檢測器

映射到高維空間后，下一步是尋找一個可以分離映射在高維特征空間中線性可分的目標與雜波的超平面： wTF -b=0，通過求解以下優化問題可以確定 w 和 b

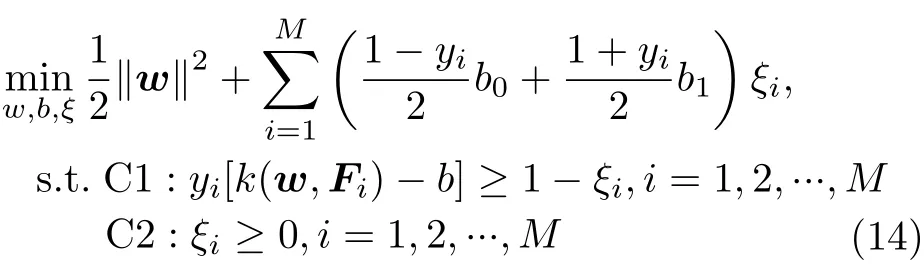
其中， ξi為松弛變量，通過控制β0和β1的變化可以用來控制虛警概率。根據SVM的理論基礎，上式可以通過序列最小優化算法來解決。得到超平面wTF -b=0 后 ， 當 wTF -b ＞0 時 ， yj=+1即 可判定為目標；當 wTF -b ≤0時 ， yj=-1即可判定為雜波。表9為其檢測結果。

基于SVM算法的特征檢測方法相較于3特征和分形檢測方法大幅度提升了檢測性能，并且能夠突破凸包學習算法的局限性，對三維以上的高維特征空間進行檢測。

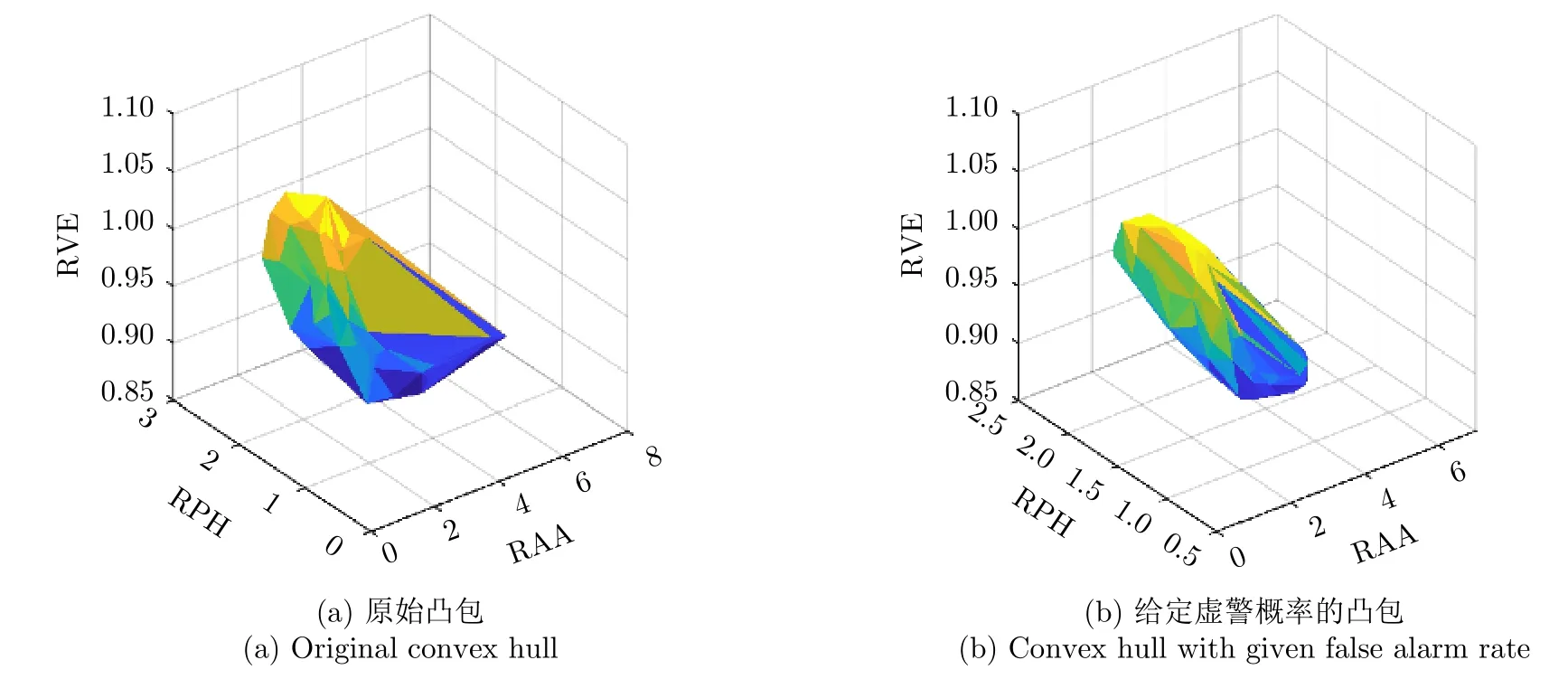
圖 31 原始數據生成的凸包和給定虛警率的凸包Fig. 31 Convex hull with the original training data and convex hull with given false alarm rate

表 9 基于SVM的檢測器與其余檢測器的性能對比[77]Tab. 9 Detection performance comparisons of SVM-based detector and the other detectors[77]

圖 32 基于決策樹的檢測器流程圖[78]Fig. 32 The flowchart of the decision-tree-based detector[78]

(3) 基于決策樹的特征檢測方法[78]。除了上文提到的基于SVM的檢測器，Zhou等人將決策樹算法和雷達目標檢測問題相結合，提出了一種基于決策樹的檢測器，并且實現了虛警的有效控制。決策樹是一種常用的分類算法，它是根據數據的屬性或特征而建立的樹狀模型。常用的決策樹算法包括ID3，分類回歸樹(Classification And Regression Tree, CART), C4.5，隨機森林(random forest)等。決策樹只有一個根節點，多個內部節點和多個葉子節點。首先，所有的訓練樣本都被分配給內部節點，其分配規則為通過選擇合適的特征和合適的閾值盡可能使得內部節點的純度最大。整個過程由上而下，遞歸進行。

文獻提取了海雜波數據中的時域Hurst指數、頻域Hurst指數以及頻譜峰值與均值比3類特征，并將其構造為三維的特征向量。對每一個特征向量，分別將目標向量貼標簽為1，雜波向量貼標簽為0，利用著名的分類回歸樹(CART)算法構造決策樹。首先，所有的特征向量處于一個根結點，通過選擇基尼指數最小(基尼指數越小，純度越大)的特征和閾值來進行分類，產生子結點。重復此類操作，直到產生的子結點不可再分，即為葉子結點。最后生成的葉子節點可以將特征空間分為兩部分。分類正確的目標樣本和所有目標樣本之比即為檢測概率。圖32為整個算法的流程圖。表10為其檢測結果。

基于決策樹的特征檢測方法將檢測與分類相結合，提升了檢測性能，同基于SVM的檢測方法一樣可以在高維的特征空間中進行檢測。

基于機器學習算法的特征檢測方法能夠對檢測性能進行大幅度的改善，由于凸包學習算法僅能利用在三維及以下的特征空間中，而機器學習算法它們均能夠突破高維特征空間的限制，意味著可以將更多的特征利用到基于特征的檢測中來，從而進一步改善檢測性能。

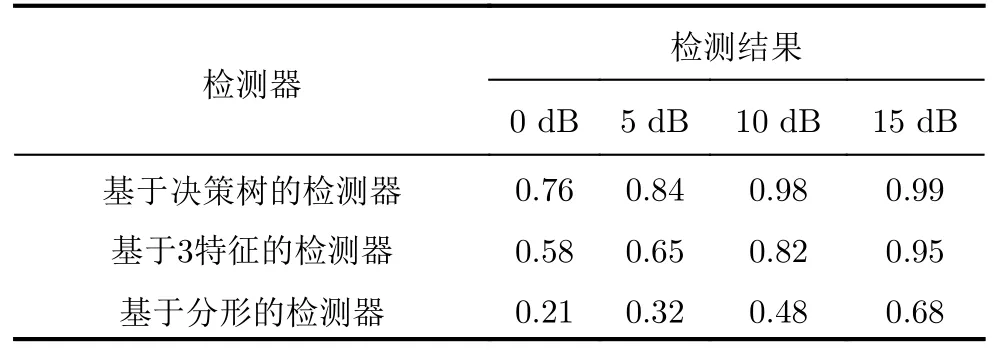
表 10 基于決策樹的檢測結果和其余檢測器的性能對比[78]Tab. 10 Detection performance comparisons of the decision tree-based detector and the other detectors[78]

4.5.2 基于時頻域3特征的檢測方法

在檢測海雜波背景下的漂浮小目標時，為了使目標回波獲得足夠的積累增益，提升檢測性能，通常需要觀測時間達到秒級，而在長時觀測的情況下，海雜波時間非平穩且紋理隨著時間變化，所以海雜波時間序列建模為時變紋理的復合高斯模型。同時，漂浮小目標回波在秒級時間尺度上呈現幅度起伏和多普勒調制，因而目標回波建模為具有幅度起伏的未知非線性調頻信號[120—122]。因此，在長的累積時間內，海雜波背景下漂浮小目標的檢測問題可以等價于在時變紋理的復合高斯雜波中尋找未知的非線性調頻信號的問題。

由于時頻分布(Time-Frequency Distribution, TFD)實現了未知調頻信號的短時相干累積，在白噪聲背景下檢測未知調頻信號時常采用TFD[120—125]。而在設計合適的TFD時，非線性調頻信號的能量可以完全集中在其瞬時頻率曲線上(Instantaneous Frequency Curve, IFC)。由于接收回波序列的歸一化時頻分布(Normalized Time-Frequency Distribu-tion, NTFD)可以增強雜波回波的時頻特性，并且目標回波可以用分段線性調頻信號近似，可以采用平滑的偽魏格納-威利分布(Smoothed Pseudo Wigner-Ville Distributions, SPWVD)[125,126]計算NTFD。海雜波和含目標的回波在NTFD上表現出了不同的特性。通過這些不同的特性可以提取3個時頻特征：NTFD的時頻累積、由NTFD亮像素構成二值圖像中的連通區域數目和最大連通區域的尺寸[75]。

同3特征檢測器的檢測步驟類似，時頻3特征檢測器同樣分為訓練部分和檢測部分。訓練部分通過接收大量的純雜波數據提取特征向量，利用快速凸包學習算法來訓練單分類器，并且為檢測部分提供均值向量和標準差向量進行歸一化處理。檢測部分通過計算待檢測單元和參考單元的接收時間序列的特征向量，利用訓練部分得到的均值向量和標準差向量進行歸一化等操作。通過對待檢測單元特征向量的計算，判斷其是否落入判決區域，從而得到判決結果。基于時頻3特征的檢測器，相較于基于原始3特征的檢測器有了一定的性能提高，然而在個別數據上檢測概率略有下降。這說明了特征提取對于聯合多特征檢測器的性能至關重要。

4.5.3 基于極化3特征的檢測方法

基于時域、頻域特征和基于時頻域特征的檢測方法對數據的處理往往只是分別使用了4個極化通道HH, HV, VH, VV，然而隨著全極化雷達的普及和雷達設備的更新換代，全極化方法在圖像處理領域越來越成熟，雷達數據全極化處理成為可能。文獻[76]嘗試使用全極化的方法處理海面漂浮小目標的檢測問題。

全極化雷達接收到的每組數據集都包含HH,HV, VH和VV 4種數據，通常使用極化散射矩陣來表征接收到的回波數據。根據散射矩陣可以提取極化相干矩陣或極化協方差矩陣。一般通過分解散射矩陣、相干矩陣或協方差矩陣來提取極化特征。對于海面漂浮小目標檢測而言，當雷達波束照射在平靜海面、海浪或是目標物體時，可能發生面散射、二面角散射和體散射。當波束照射在平靜海面或是在垂直浪面以及在目標表面鏡面反射時，會發生面散射；當波束照射在海浪形成的二面角或是目標與海面所形成的二面夾角時，可能會發生二面角散射；而當波束照射在破碎的浪花(白冠)或是目標復雜結構內時，將會發生體散射。雷達波束照射區域內有無目標會影響照射區域的散射類型和散射能量的大小，由此可以利用該差異性提取相關極化特征進行漂浮小目標檢測。

基于極化目標分解理論基礎，文獻[76]根據海面漂浮小目標檢測場景，選取Freeman-Durden三分量分解方法[127]分別對3種散射機制進行建模，確定3種散射機制下的能量大小，選取待檢測單元和參考單元能量的相對比值從而提取到3個極化特征，分別為相對體散射機制對應能量、相對二面角散射機制對應能量和相對面散射機制對應能量。利用這3類特征通過凸包學習算法對海面漂浮小目標進行特征檢測。圖33為極化3特征與原始3特征的檢測性能對比圖。

基于極化3特征的檢測方法與原始單極化工作方式下的基于原始3特征的檢測方法相比，檢測器性能有了一定的提升且檢測器具有魯棒性。由于基于極化3特征的檢測方法利用了4個極化通道的雷達數據從而提取到具有可分性的雜波和目標特征，所以檢測效果比基于單極化工作方式的檢測器效果更優。利用全極化信息進行檢測可以充分利用雷達所接收到的信息，有效提升檢測性能，可以在此對特征提取進行進一步的研究。

5 特征檢測的發展趨勢和需要重點關注的問題

5.1 發展趨勢

海雜波背景下漂浮小目標的檢測是一類國內外公認的難題，隨著海面目標隱身化與小型化，提高對漂浮小目標的檢測能力對于海面目標檢測具有重要意義。基于特征類的漂浮小目標檢測方法經歷了多個發展階段，從提取單一特征進行檢測到聯合3特征的檢測方法再到基于機器學習算法的高維特征空間檢測；而提取特征的范圍也從時域、頻域的一維變換為時頻域的二維，且不拘泥于單極化的工作模式，轉而向全極化工作模式下的特征發展，本文介紹了現有的幾種基于特征的漂浮小目標檢測方法，簡單分析了它們的檢測原理，其檢測性能各有優劣。現有的檢測器仍有充足的發展空間。為了進一步提升檢測概率，改善檢測器性能，未來基于特征的檢測器的發展方向可以從以下幾個方面來進行研究：

(1) 提取更多能夠有效區分雜波和目標的特征。接收的雷達信號中包含大量的雜波和目標各個方面的信息，利用時域、頻域及時頻域等不同變化域和不同層面的雜波與目標的各類信息，提取新的適用于特征檢測的特征。雜波與目標在特征空間中的可分性越強，說明該特征更適用于特征檢測，所得到的檢測器擁有更強的檢測性能。

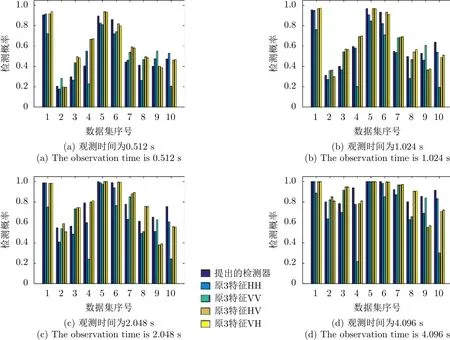
圖 33 極化3特征檢測方法與原始3特征檢測方法檢測概率柱狀圖[76]Fig. 33 Detection probabilities of polarization features-based detector and tri-detector at HH, VV, HV, and VH polarizations for ten data sets[76]

(2) 利用新興學科改進檢測算法。異常檢測下對單分類器的設計常采用的凸包類學習算法具有一定的局限性，即無法對高維特征向量進行處理。隨著人工智能的發展，越來越多的學習算法能夠利用到特征檢測中來，二者之間的學科融合已經成為發展趨勢，它們可以突破高維特征空間的限制，能夠將更多的特征利用到特征檢測中，從而使檢測性能進一步改善。

(3) 發展新體制雷達。基于特征的檢測方法在檢測過程中需要較長的觀測時間，而在實際應用中的雷達往往達不到所需長時間觀測的要求。傳統雷達一個波位上的長駐留時間和掃描效率之間的沖突是難以調和的，這也是無法長時觀測的原因。2003年，MIT的林肯實驗室提出了使用MIMO數字陣的泛探雷達的概念[128]，實現了在所有方向下的全時間觀測。這類新體制雷達的發展，更有利于對雜波和目標特征的提取，在特征空間的可分性越強，所設計的檢測器更能達到良好的性能。

5.2 需要重點關注的問題

(1) 由于軍事應用的特殊性，人工智能在軍事領域應用的廣度和深度遠遠不及互聯網商業領域。而這種差異與軍事人工智能系統可用的數據有很大關系。以海面目標檢測為例，對于非合作目標很難收集到足夠的數據來訓練相應的人工智能算法。人工智能算法(尤其是深度學習)通常需要大量數據，這些數據必須經過精確標記，并與每個特定問題域相關。在有關軍事局勢的信息被損壞或者得到的數據集不完備，我們做出的決策可能遠非最佳。因此，小樣本或者殘缺樣本下的基于人工智能的海面目標檢測需要進一步研究。

(2) 隨著機器學習模型復雜度的日益增加，對于目前常用的機器學習方法，我們已經無法從直觀上去理解機器如何做出決策。如果僅僅將機器學習模型用來推薦一部電影或者推薦一家餐廳，我們可能并不需要模型對結果做出解釋，但是在雷達對海目標檢測領域，我們不僅希望知道模型結果，還需要了解這些決策是如何做出來的。當前模型的可解釋性技術，主要是對輸入的各個特征進行定量評價，找到對結果影響最大的特征。或者進行進一步的分析，考察特征的相關性。對于列表型數據，每一列即為一個特征；而對于圖像、文本或其他非列表型數據，我們還需要先對其進行預處理，構建易于理解的特征。可解釋性是機器學習的一個重要的研究方向，也同樣是對海目標檢測領域邁不過去的一道坎。因此，如何設計可解釋的人工智能方法是需要研究的重要課題。

(3) 基于人工智能的方法，學習是其中的重中之重。人的學習學的不是知識，而是獲取數據、信息、知識經驗的方法；而機器的學習學的是數據、信息和知識，還不會活學活用。對于雷達探測來說，準確的檢測器設計必須建立在大量不同情況下的海量數據之上，而這種學習的過程必然耗費大量的時間，對于瞬息萬變的戰場環境，特別是海面環境的高動態變化，基于人工智能方法的檢測器的檢測準則確定的速度嚴重依賴于算法特別是硬件平臺的計算能力，因此，將人工智能推向實用的有一個重要的難點是算法設計的高效性以及硬件平臺計算能力的不斷提升。

6 結束語

本文首先分析了目前對海探測面臨的熱點和難點問題，并介紹了目前常用于進行特征檢測算法驗證的數據集，隨后具體說明了基于特征的檢測方法的原理，同時介紹了幾種海雜波背景下基于特征的海面慢速、漂浮小目標檢測方法，并對它們的檢測性能進行了分析。海面慢速、漂浮小目標的檢測對于海洋軍事的發展具有重大的意義，如何提高海面弱小目標智能檢測的性能，是當前研究的重點。隨著新興學科的發展，雷達目標檢測與各類新興學科的融合已經成為了發展趨勢。將新興學科的智能化與基于特征的檢測方法結合，能夠更有效地對目標進行檢測，改善海雜波背景下慢速、漂浮小目標的檢測性能。