復合固體推進劑脫濕過程細觀建模與損傷定量表征①

張 超，侯俊玲，李 群

(西安交通大學 航天航空學院 機械結構強度與振動國家重點實驗室，西安 710049)

0 引言

復合固體推進劑作為一種含能材料，在航天航空領域得到了非常廣泛的應用，是固體火箭發動機不可維修的最薄弱環節之一。固體推進劑的結構完整性直接影響著導彈武器的貯存和使用情況，必須在使用前就對其力學性能進行準確預測。早期關于固體推進劑力學行為的研究，主要是從連續介質力學角度基于唯象理論建立其本構關系[1-2]，這些理論均將固體推進劑作為連續均勻介質來處理。然而，在細觀尺度上，固體推進劑是一種高填充比顆粒增強復合粘彈性材料，主要由以高分子聚合物為基體的粘合劑HTPB和大量的AP顆粒及金屬燃料(Al)顆粒組成，其力學行為主要由固體填料的體積分數、粒徑大小、粘合劑基體的粘彈性質以及粘合劑基體與固體填料之間的界面性質所決定。因此，從細觀角度出發研究固體推進劑的力學行為具有重要意義。

要從細觀角度出發研究固體推進劑的力學行為，首先要建立能夠有效表征固體推進劑細觀結構的顆粒填充模型。在已發表的文獻中，關于顆粒復合材料填充模型的建立，主要分為兩類：第一類是通過實驗觀測的內部微結構重構，建立材料的真實細觀結構[3]，其能夠準確反映材料的真實細觀結構，但對試驗條件和技術手段等均有較高的要求，在相關圖像和數據的處理過程中工作量巨大，成本十分高昂。關于顆粒填充復合材料細觀結構建模，學者們大多采用第二類方法，即通過數值模擬仿真方法，對材料典型細觀結構進行建模[4-8]。例如，基于蒙特卡羅[9]算法的隨機模擬算法和基于分子動力學[10]算法的碰撞模擬方法建立二維顆粒填充模型。近年來，為建立高體積分數三維顆粒填充模型，學者們進行了大量的研究，并取得了不錯的成果。例如，Zhang等[4]提出的下落堆積法、Yu等[6]提出的空間壓縮法和傳統的隨機序列吸附法[7]。但是，采用這些方法，在顆粒填充過程中，當顆粒體積分數高于50%時，往往會遇到顆粒投放重疊檢測迭代次數大、建模時間過長甚至失效的問題，無法達到材料配方所要求的體積分數。因此，亟需要開發一種建立高體積分數三維顆粒填充模型的算法，以便開展高體積分數顆粒填充復合材料的數值仿真研究。

此外，大量研究結果表明[11-22]，顆粒/基體界面脫濕是固體推進劑在外界載荷作用下的主要失效形式。針對推進劑顆粒/基體界面脫濕問題，國內外學者們開展了大量工作，探究了細觀結構損傷演化規律及其對宏觀力學行為的影響。袁嵩等[23]建立 了簡化的單顆粒和多顆粒細觀結構模型，研究了顆粒與粘合劑基體在粘結完好和存在脫粘兩種情況下固體推進劑內部的應力分布。Matous K等[24]建立了推進劑代表體積單元的細觀模型，數值模擬了顆粒/基體界面損傷的產生及發展。李高春等[25]綜合考慮固體推進劑細觀損傷的特點，研究了推進劑的界面脫濕過程及其對宏觀力學性能的影響。張建偉[26]、職世君[27]等研究了固體填料的體積分數、顆粒位置的隨機分布、粒徑大小對推進劑細觀損傷及宏觀力學性能的影響。目前，研究大多集中于二維模型或三維空間低顆粒體積分數模型，開展高體積分數的固體推進劑三維細觀數值模擬，能更好為地反映受載條件下固體推進劑的細觀損傷特性，進而為固體推進劑的使用與配方設計提供指導。

本文基于隨機序列吸附法、熱膨脹原理及分步填充的思想，實現了高體積分數顆粒填充，并通過幾何合并的方式，加入粘合劑基體和顆粒/基體界面，建立固體推進劑三維細觀結構模型。引入內聚力界面單元，基于雙線性損傷內聚力模型，考慮粘合劑基體的粘彈特性，研究不同應變率加載下固體推進劑材料內部的界面脫濕行為，并基于內聚力模型定義損傷變量，對其細觀損傷進行了定量表征。

1 三維細觀結構模型

本文以HTPB推進劑[11]為研究對象，其主要成分包括HTPB基體、AP顆粒、Al顆粒以及其他助劑，其基本組分的比例見表1。HTPB推進劑是一個典型的顆粒填充復合材料，其顆粒的粒徑分布情況如圖1所示[10]。

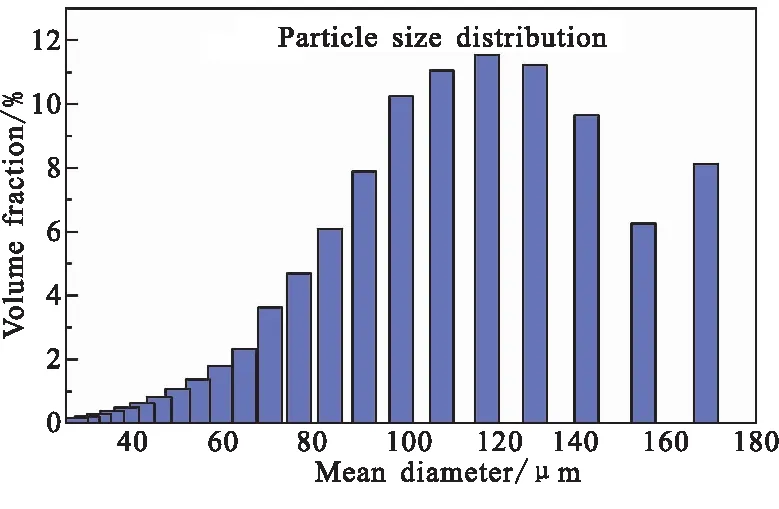
圖1 固體推進劑顆粒粒徑分布Fig.1 Particle size distribution of solid propellants

本文基于隨機序列吸附法、熱膨脹原理及分步填充的思想，實現了高體積分數顆粒填充，詳細顆粒填充流程如圖2所示。在三維細觀結構顆粒填充過程中，首先將顆粒粒徑等比例縮小，基于隨機序列吸附法，運用Matlab編程語言，向胞元內隨機投放小顆粒，記錄小顆粒的粒徑、熱膨脹系數和球心坐標。然后，使用Python腳本語言進行Abaqus二次開發建立初始模型，通過熱膨脹分析提高顆粒粒徑。建模過程中，為提高效率，每一輪填充的顆粒數不宜過多，需要經過多步填充和熱膨脹過程，才能夠建立高體積分數三維細觀結構模型。需要注意的是，若顆粒初始粒徑過小，會造成熱膨脹分析過程中有限元網格畸變和收斂的困難。因此，小顆粒粒徑的選取應以顆粒初始體積分數不小于實際體積分數的33%為宜。

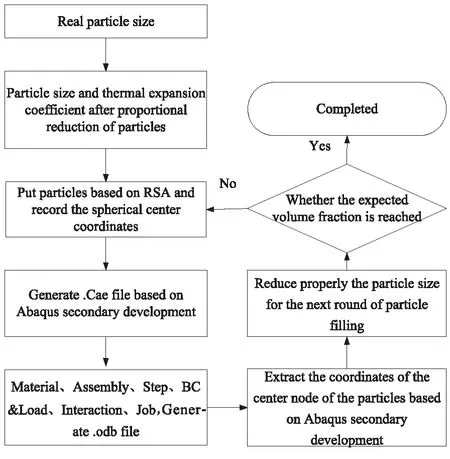
圖2 三維細觀結構顆粒填充流程圖Fig.2 Particle filling flowchart of three dimensional mesostructure

三維細觀結構建模過程詳細說明如下：

(1)第一輪顆粒填充：考慮到大顆粒對固體推進劑的力學行為影響較大，首先基于隨機序列吸附法，將大顆粒以真實粒徑由大到小依次填充進胞元內，直至單個顆粒的重疊檢測次數等于預設值，顆粒填充效果如圖3(a)所示，顆粒數為6，顆粒體積分數為31.49%。因為大顆粒是以真實粒徑填充的，因此不需要進行熱膨脹分析。

(2)第二輪顆粒填充：在第一輪填充顆粒的基礎上，進行第二輪顆粒填充時，為保證熱膨脹分析的收斂性并減小計算量，第二輪填充進12個顆粒，此時胞元內共有18個顆粒，體積分數達到40.72%，第二輪顆粒填充初始狀態及網格劃分如圖3(b)所示。特別需要注意的是，在熱膨脹分析過程中，裝配體不包含粘合劑基體和顆粒/基體界面部件，在顆粒填充完成后，通過幾何合并的方式將粘合劑基體和顆粒/基體界面加入裝配體即可，同時在模型中引入通用接觸以防止顆粒重疊。

(3)第二輪填充顆粒熱膨脹分析：在熱膨脹分析過程中，建立6個薄壁面并完全固定，以保證顆粒在熱膨脹分析過程中始終處于胞元所在的空間內。顆粒熱膨脹分析后的應變和位移云圖分別如圖3(c)、(d)所示，熱膨脹分析后顆粒體積分數為45.05%，較第二輪填充的初始狀態提高了4.33%。由圖3(c) 、(d)可見，在顆粒熱膨脹分析過程中，隨著溫度逐漸升高，第二輪填充的顆粒粒徑不斷增大，并可通過顆粒與薄壁面、顆粒與顆粒之間的相互作用，使顆粒產生剛性位移，將每一個顆粒重新分配到合適的位置。但當其中某些顆粒不存在理論膨脹空間時，即使在其他顆粒仍有膨脹空間的情況下，熱膨脹分析過程也會出現不收斂的情況，導致熱膨脹分析終止。

(4)第二輪部分顆粒熱膨脹分析：基于Python腳本語言進行Abaqus二次開發，提取所有顆粒中心節點的坐標，并根據熱膨脹系數和熱膨脹分析時間計算顆粒當前粒徑，重新建立模型。同時，將第二輪沒有理論膨脹空間的顆粒熱膨脹系數置為零，僅對有膨脹空間的顆粒進行熱膨脹分析，再次提高顆粒體積分數，圖3(e)、(f)分別為僅對某一個顆粒進行熱膨脹分析的應變和位移云圖。同理，對其他有膨脹空間的顆粒進行熱膨脹分析，直至所有顆粒都不存在理論膨脹空間時，第二輪熱膨脹分析結束，此時顆粒體積分數為47.95%，再次提高2.9%。

(a)Particle filling effect of the first round (b)Initial state and grid division of particle filling

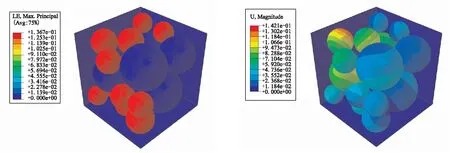
(c)Strain distribution of particle thermal expansion analysis (d)Displacement distribution of particle thermal expansion

(5)重復步驟(2)～(4)工作，將更多顆粒填充進胞元內，最終可得到胞元尺寸為0.613 3 mm3，顆粒數為150，顆粒體積分數為63.8%的三維細觀結構模型，如圖4所示。

圖4 顆粒填充細觀模型(體積分數為63.8%)Fig.4 Particle filled mesoscopic model (volume fraction is 63.8%)

2 界面脫濕數值模擬

2.1 推進劑組分參數

HTPB推進劑的主要組分如表1所示，在數值模擬過程中，主要參數為固體填充顆粒的彈性模量和泊松比，以及粘合劑基體的松弛模量。由于AP顆粒的彈性模量遠大于粘合劑基體的彈性模量，在相同載荷的作用下，相較于基體的變形，AP顆粒的變形可忽略不計，故假設AP顆粒為彈性體，其彈性模量EAP=32 450 MPa，泊松比vAP=0.143 3[3]。同時，為了進一步簡化計算模型，將Al顆粒對固體推進劑力學性能的影響等效到基體中考慮，文中Al顆粒和粘合劑基體混合物的初始彈性模量設為7.39 MPa[3]。

HTPB推進劑粘合劑基體具備粘彈性材料的基本性質，是導致推進劑具有粘彈性的根本原因，粘合劑基體松弛模量依據文獻[28]中推進劑應力松弛實驗結果選取，對松弛曲線用Prony級數的形式進行擬合，其擬合的表達式為

(1)

式中t為時間；E∞為平衡模量，是t→∞時模量的穩態模量；Ei和τi分別為第i個Maxwell單元的模量和松弛時間。

所得Prony級數表達式的各項系數見表2，進而得到粘合劑基體的松弛模量應力應變關系為

(2)

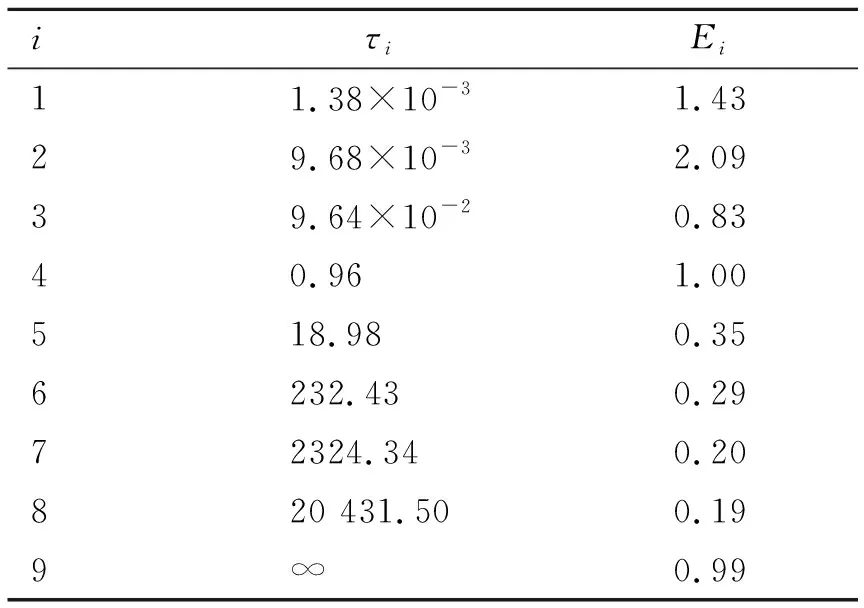
表2 HTPB推進劑松弛模量Prony級數表達式系數Table 2 Prony series expression coefficient of relaxation modulus of HTPB propellant

2.2 內聚力模型及參數

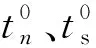
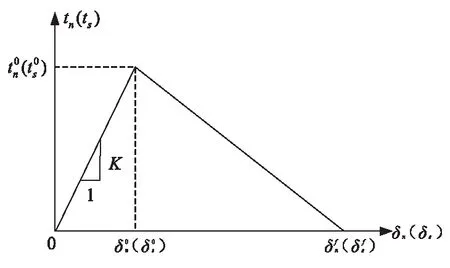
圖5 雙線性內聚力模型Fig.5 Bilinear cohesion model

本研究中，損傷初始階段采用最大應力準則，其控制方程為

(3)

雙線性內聚力模型張力位移關系的控制方程為

(4)

其中，D為損傷因子，定義為

(5)

雙線性內聚力模型主要包括3個參數：初始線性模量、最大應力值和最終開裂位移值。本研究中，參考文獻[25]中雙線性內聚力模型數據，初始線性模量取為基體模量的10倍；界面最大應力取為0.73 MPa；最終開裂位移值取為37 μm。

2.3 有限元網格及邊界條件

在有限元網格劃分過程中，AP顆粒采用結構化網格劃分技術，單元類型為C3D8R，共20 424個單元；界面采用結構化網格劃分技術，單元類型為COH3D8，共10 320個單元；由于顆粒的存在，導致基體結構非常復雜，采用自由網格劃分技術，單元類型為C3D10，共83 676個單元。AP顆粒和界面網格劃分如圖6(a)所示，粘合劑基體網格劃分如圖6(b)所示。

(a)Mesh of AP particles and interface

(b)Mesh of adhesive matrix圖6 細觀模型網格劃分Fig.6 Mesh of mesoscopic model

為模擬固體推進劑在均布位移載荷條件下的力學行為，采用如下邊界條件：面EFGH保持固定，約束面ADHE、面BCGF、面ABFE和面DCGH的法向位移，在面ABCD沿x軸正方向施加均布位移載荷，如圖7所示。同時，在模型中引入通用接觸以防止界面脫濕后導致的界面之間相互滲透。

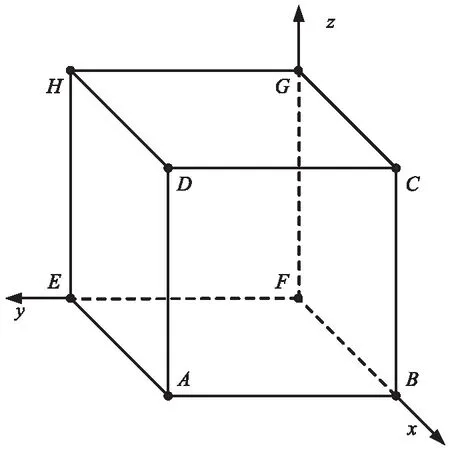
圖7 細觀模型邊界條件Fig.7 Boundary conditions of mesoscopic model

3 結果與分析

3.1 脫濕過程數值模擬結果

基于雙線性損傷內聚力模型，考慮粘合劑基體的粘彈特性，對所建三維細觀結構模型進行不同應變率下的單軸拉伸數值模擬，HTPB推進劑在不同應變率下的單軸拉伸應力-應變曲線如圖8所示。由圖8可見，固體推進劑在不同應變率載荷下表現出不同的力學行為，應變率越高，應力-應變曲線的斜率越高，材料表現出更高的剛度。圖9和圖10分別給出應變率為3.33×10-3s-1，應變分別為3%、8%和13%時，對應的固體推進劑內部Mises應力和剛度衰減率SDEG損傷云圖，其中剛度衰減率SDEG是Abaqus后處理結果中表征材料剛度衰減率的變量，當SDEG=0時表示材料沒有損傷，SDEG=1時表示材料已經完全損壞。

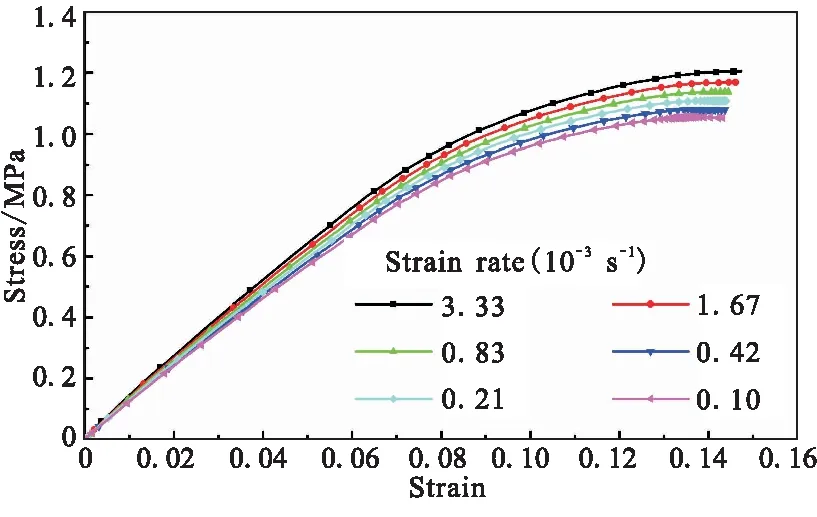
圖8 HTPB推進劑單軸拉伸應力-應變曲線Fig.8 Uniaxial tensile stress-strain curves of HTPB propellant

圖9(a)和圖10(a)分別為應變為3%時的Mises應力和SDEG損傷云圖。在應變為3%時，應力-應變呈典型線性階段(如圖8所示)。此時，在均布位移載荷的作用下，由于顆粒與基體、顆粒與顆粒之間的相互作用，在大顆粒的極區位置產生很高的局部應力場，但顆粒與基體仍然處于彈性變化范圍，材料內部尚未出現界面脫濕損傷。

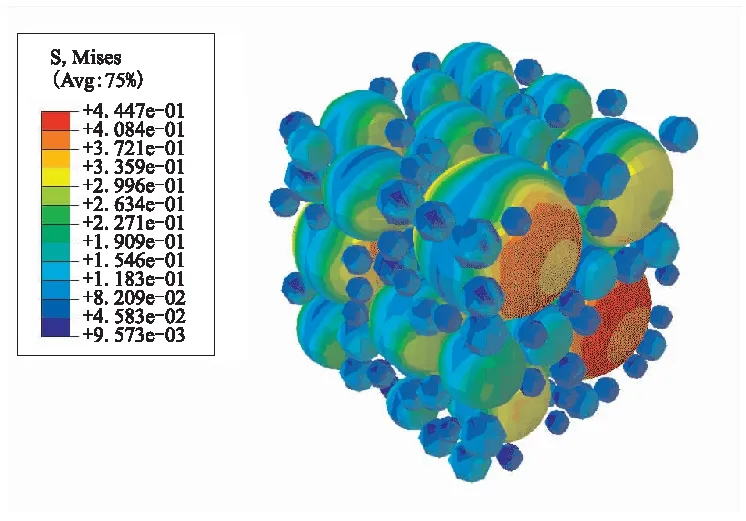
(a)Strain is 3%

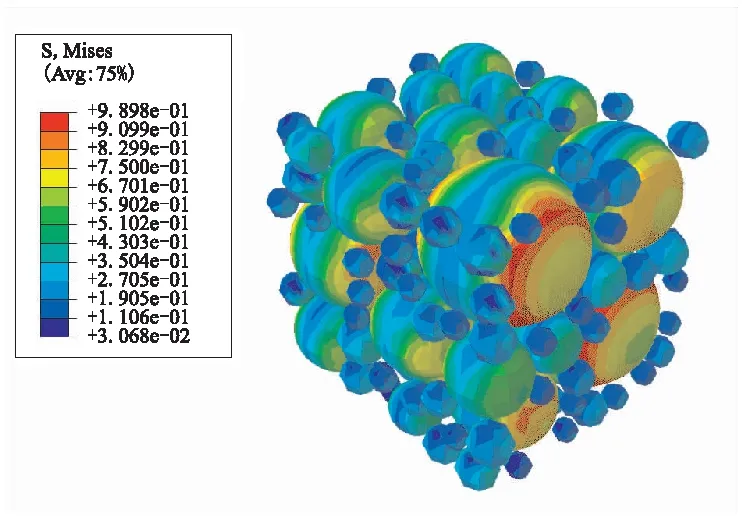
(b)Strain is 8%

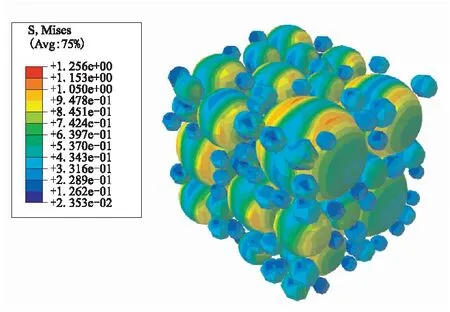
(c)Strain is 13%圖9 固體推進劑Mises應力云圖Fig.9 Mises stress distribution in solid propellants

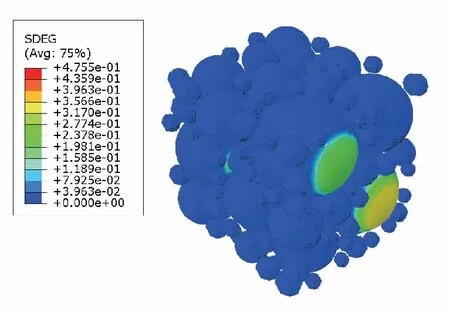
隨著應變增加到8%，如圖9(b)和圖10(b)所示，在大顆粒的極區位置應力集中明顯，出現了一定的界面損傷。這是因為顆粒與基體的材料屬性不同，顆粒模量遠大于基體模量，在作用力相同情況下，顆粒變形小于基體變形，使得界面成為最薄弱的部位，故界面最先出現損傷，且因界面損傷導致顆粒承載能力下降，材料等效模量降低。從圖8所示的應力-應變曲線也可看出，在8%應變處，應力應變呈非線性關系，表現出一定程度的軟化，這表明材料內部出現了一定的界面損傷。

由圖9(c)和圖10(c)可知，隨著加載繼續進行到應變為13%時，在比較密集的顆粒附近，也出現了大量的界面損傷，且在顆粒界面損傷嚴重的區域，Mises應力進一步降低。這說明，由于界面損傷導致大顆粒承載能力進一步下降，材料等效模量迅速減小。對比圖8所示的應力-應變曲線，在應變為13%時，應力-應變呈強非線性關系，且軟化加劇，表明材料內部出現了大量的界面損傷。

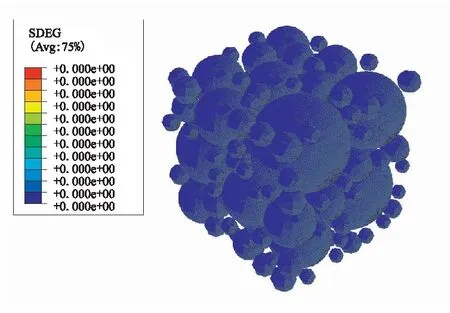
(a)Strain is 3%

(b)Strain is 8%

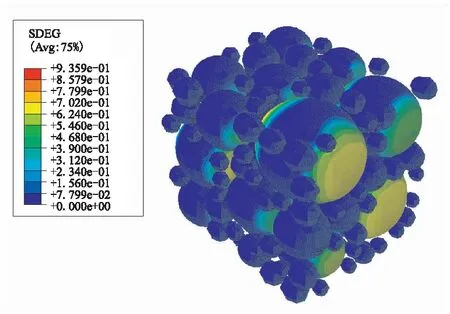
(c)Strain is 13%%圖10 固體推進劑SDEG損傷云圖Fig.10 SDEG distribution in solid propellants

3.2 基于界面剛度衰減率的脫濕損傷定量表征

為了更好表征固體推進劑材料的界面脫濕行為，本文提出一種基于界面剛度衰減率的損傷定量表征方法。定義固體推進劑材料內部脫濕面積總和(DA)為

(6)

式中ED(i)為第i個界面單元的損傷體積；d為界面單元的厚度；N為所有界面單元的個數。

ED(i)定義為

(7)

式中SDEG(j)為第i個界面單元第j個高斯積分點的剛度衰減率；V(j)為第i個界面單元第j個高斯積分點的幾何體積；n為第i個界面單元的高斯積分點個數。

選取顆粒體積分數為63.8%的固體推進劑細觀模型，圖11展示了不同應變率加載情況下，脫濕面積DA隨載荷的變化情況。

(a)Dewetting area-strain

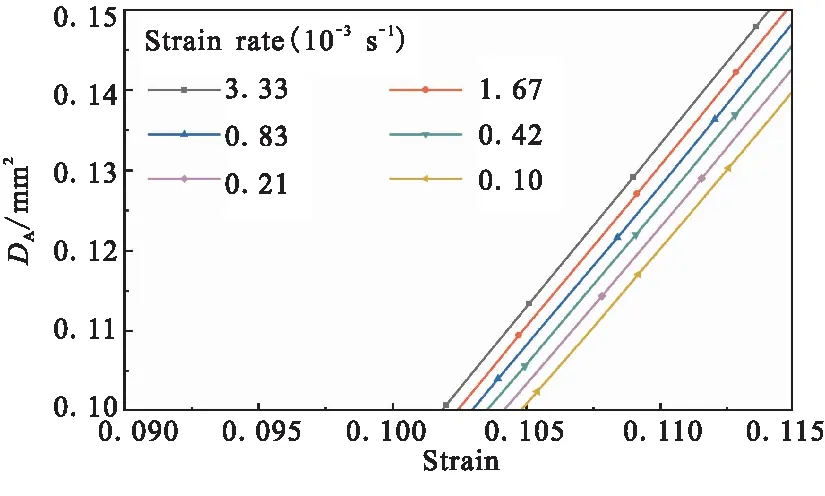
(b)Enlarged view partially圖11 損傷-應變曲線Fig.11 Damage-strain curves

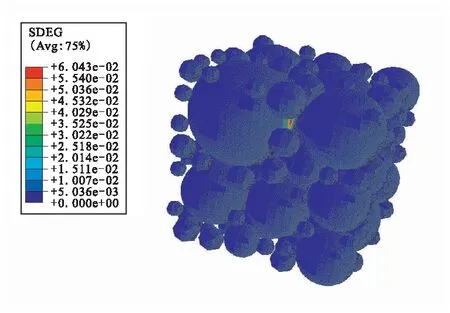
從圖11(a)和12(a)中可看出，在低應變載荷情況下，損傷面積DA=0，表明材料處于彈性范圍內，內部沒有出現界面損傷。而當應變超過6%附近時，隨時載荷的增大，脫濕面積DA的值顯著增大，這表明材料內部出現界面損傷。圖11(a)所示的脫濕面積DA的拐點，可認為是材料的初始脫濕點，其應變載荷值大約在6%附近，如圖11(b)和12(b)所示。隨著載荷增大，DA值逐漸急劇增大，表明其損傷狀態嚴重，如圖11(c)和12(c)所示。

此外，從圖11(b)給出大應變載荷的損傷面積局部放大圖中可以看出，在相同應變的情況下，應變率越高，材料內部脫濕面積越大。這是由于粘合劑基體具有與時間相關的粘彈特性，在相同應變的情況下，應變率越高，加載時間越短，材料內部應力越大(如圖8所示)，更易造成界面損傷。

(a)Strain is 3%

(b)Strain is 6%

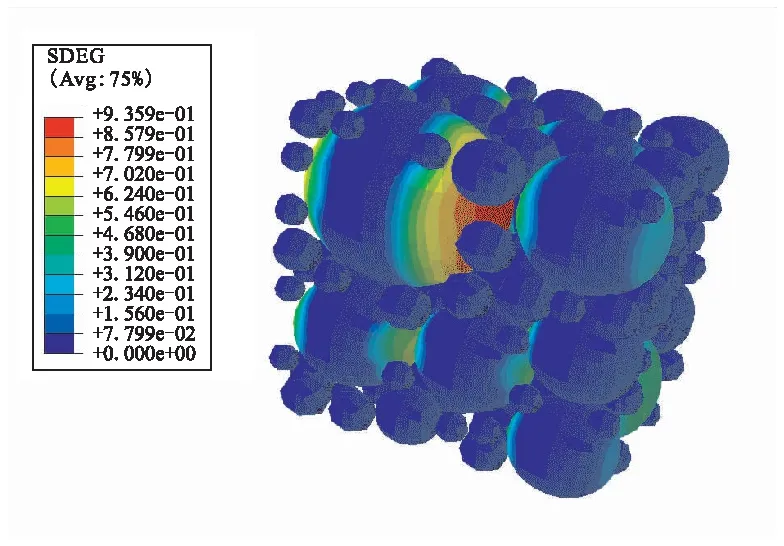
(c)Strain is 13%圖12 剛度衰減率SDEG損傷云圖 (strain rate=3.33×10-3 s-1)Fig.12 SDEG damage distribution (strain rate=3.33×10-3 s-1)

4 結論

(1)基于隨機序列吸附法、熱膨脹原理和分步填充的思想，實現了高體積分數顆粒填充，并通過幾何合并的方式，加入粘合劑基體和顆粒/基體界面，建立了高體積分數固體推進劑三維細觀結構模型。所建模型能有效表征固體推進劑的三維細觀結構。

(2)基于雙線性損傷內聚力模型，在顆粒/基體界面嵌入內聚力單元，考慮粘合劑基體與時間相關的粘彈特性，對不同應變率下固體推進劑內部脫濕過程進行了數值模擬。結果表明，由于顆粒與基體材料屬性相差較大，脫濕首先出現在大顆粒及顆粒比較密集的區域，界面損傷導致材料承載能力下降；且應變率越高，材料內部越容易出現損傷。

(3)使用Python腳本語言進行Abaqus二次開發，提取所有內聚力界面單元高斯積分點的幾何體積和剛度衰減率SDEG數據，定義固體推進劑材料內部脫濕面積，可準確捕捉固體推進劑顆粒/基體界面的脫濕點，并對其細觀損傷進行定量表征。