創設雙曲線作圖情境 再認識反比例函數
——幾何畫板軟件提升互動體驗線上教學實錄*

趙欣慶 (甘肅省蘭州市永登連鋁學校 730335)

1 學情分析

上課班級是地處遠郊的市級示范高中高三年級兩個理科班．同一時間兩個班進行線上高中數學教學，師生協同實現教學共振需要信息技術支持．選擇幾何畫板軟件作為工具，因其具有文檔選項添加頁功能，具有把文檔片段及插入公式以粘貼圖片的方式編輯在其界面上的優勢；更重要的原因是師生對幾何畫板軟件動態構圖情有獨鐘，加之學生人手一臺電腦，具有跟隨教師操作幾何畫板軟件的能力．

2 內容分析

作為平面解析幾何“雙曲線”復習內容的完備，在線上教學中，運用幾何畫板軟件創設反比例函數圖象作圖情境.學生先在微信群中表達自己的看法，教師快速地了解每一位學生的觀點后，引導學生線上共同操作“幾何畫板”作圖，更加有效地回應學生，營造積極互動的學習氛圍；深刻認識反比例函數圖象，理解雙曲線的本質，揭露雙曲線與反比例函數的關系．

3 過程實錄

在高中數學線上教學中，將幾何畫板軟件作圖融入到線上互動環節，對激發學生的操作熱情，引導學生深度地體驗數學知識并培養學生的實踐能力，提升對比較抽象的高中數學知識的深入理解是極其有益的．高中解析幾何教學，要求學生會用坐標法解決幾何問題，如果輔以準確的幾何作圖，將加深學生對問題的理解．為此，創設一個求曲線方程的引例，得到雙曲線與反比例函數的關系.在教師的引導下，師生共同操作幾何畫板作圖，創設反比例函數圖象的作圖情境，分析雙曲線的性質，再認識反比例函數圖象，解析雙曲線的本質．

3.1 問題情境

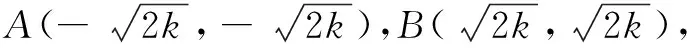
“臺上十分鐘，臺下十年功”．在教師的教學設計中應以文檔形式以及插入公式詳盡全面地準備問題情境．首先展示引例．通過觀察、思考情境問題，微信群里有學生發現題目中蘊含著雙曲線定義．

生：平面上到兩個定點的距離之差的絕對值為定值的點的軌跡可能是雙曲線，題目中的兩個定點A和B不在坐標軸上，而在直線y=x上，且關于直線y=-x對稱．

教師引導學生用直譯法,按求動點的軌跡方程的基本步驟解題，每一步驟的結果先由學生得到，討論確定后，再由教師按步驟將結論粘貼在幾何畫板上．

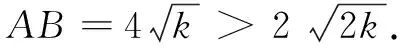
生：計算可要細心啊！

微信群中學生表示準確計算的重要性．

師：同學們，解析過程運算嚴密，體現了求軌跡方程的純粹性與完備性，這是數學的推理美．重要的是同學們發現結論為二次曲線的軌跡方程具有對稱性，變形后恰為反比例函數的標準形式．

學生紛紛表達自己的看法，有現場比較幾何畫板繪制圖象與尺規作圖的意愿．

3.2 具體情境

生：參數k取一個正數，是不是可以簡化問題？可以畫出已知反比例的函數圖象．

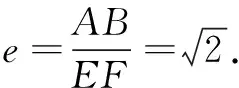
師：同學們可根據離心率的概念計算引例中雙曲線的離心率．

3.3 作圖情境

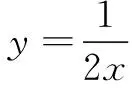
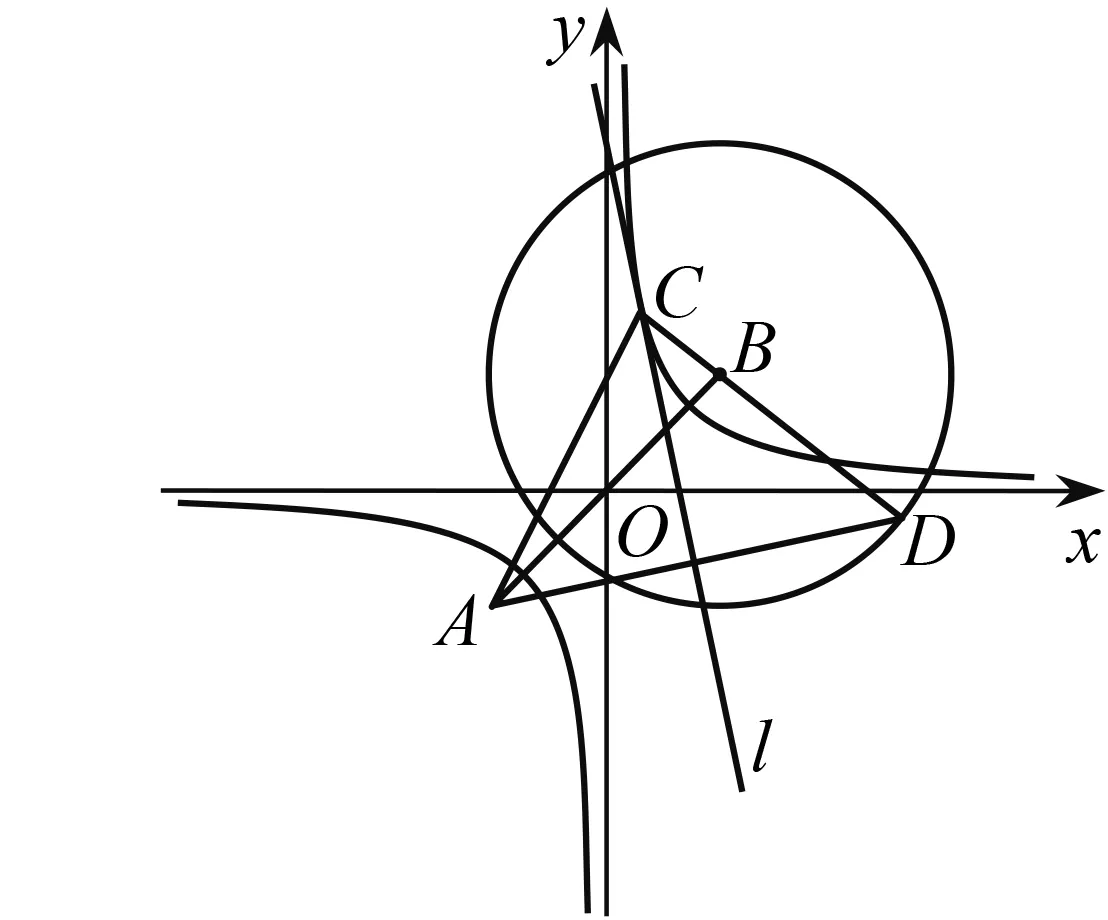
圖1

探索 打開幾何畫板，建立平面直角坐標系，描繪點A(-1,-1)，B(1,1)；以點B為圓心，以定長2為半徑作圓.由于要在這個圓上任取一個主動點，把這個圓稱為“控制圓”．在控制圓上任意選取一點D．作直線DA的中垂線l與直線DB相交于點C．同時選取D,C兩點，構造軌跡(圖1)．根據雙曲線的定義，由中垂線的對稱性質，得|CA-CB|=CD-CB=BD=2．

3.4 動態情境

生：雙曲線與其漸近線越來越近，永不相交，怎么理解？

圖2

探析 當點C在雙曲線第一象限的一支上時，鼠標拖動點D在控制圓上逆時針方向勻速旋轉，發現點C在雙曲線上加速在向右移動，這時候等腰△ADC底邊AD上的高GC越來越大，當直線DB接近平行于x軸時，等腰△ADC的兩條腰接近于平行，點C與x軸正方向無限逼近．超越平行，等腰△ADC的頂點C出現在第二象限，這時若順時針微調控制圓上的點D，發現點C與x軸負方向無限逼近(圖2)．

生：這時切線l幾乎與x軸平行，但又不能平行．

圖3

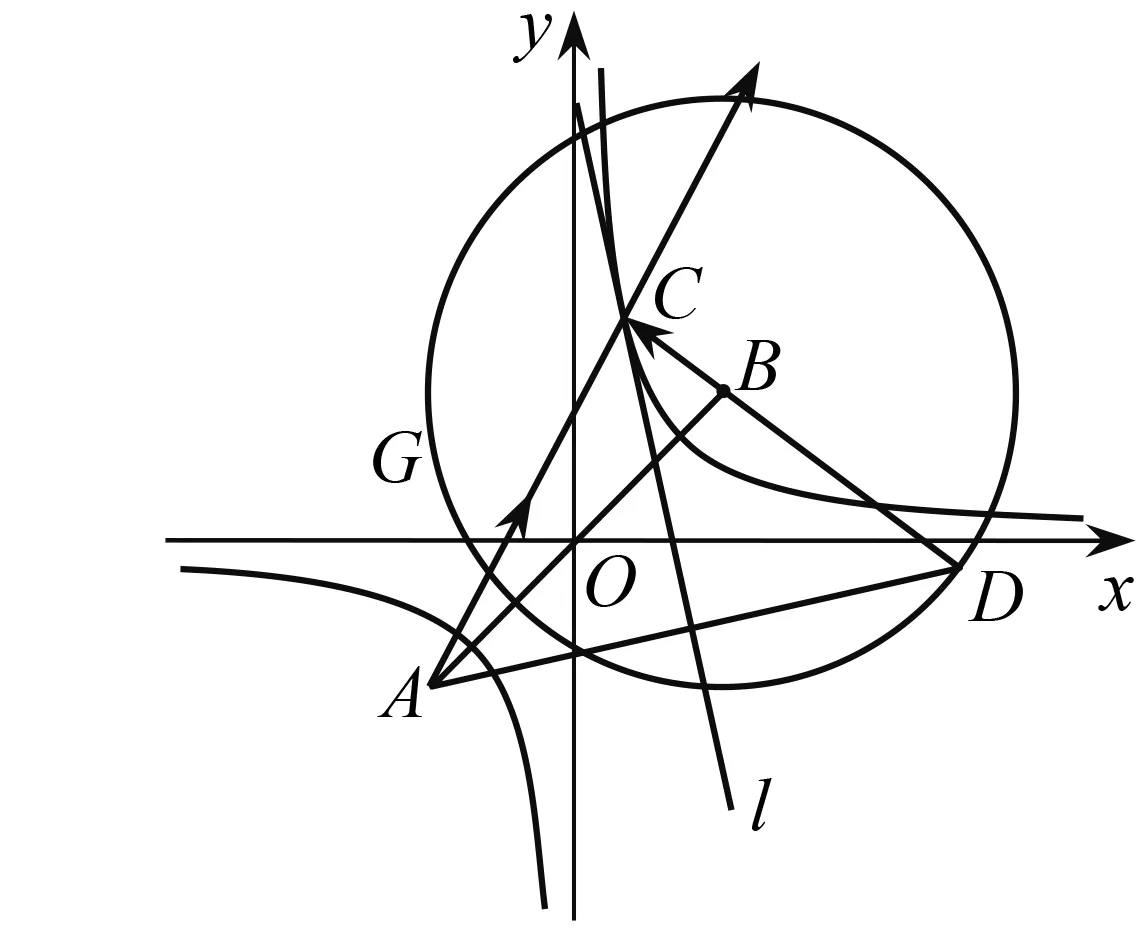
圖4

3.5 光學性質

問題反比例函數圖象的光學性質．

探析 拖動點D在控制圓周上旋轉，切線l伴隨切點C緊貼著反比例函數圖象運動.觀察發現，從雙曲線焦點B出發的光線，經過雙曲線反射，本質是由雙曲線的切線反射，就好像是從焦點A射出的一樣(圖4)．

師：等腰△ACD的頂角∠ACD的角平分線l即為過點C的切線，又根據對頂角的性質，得到入射角等于反射角的光學性質．

4 結語

高三在線教學輔學雙曲線時，在教師的引導下，師生共同操作幾何畫板軟件，探索圖形、問題共答，將數學推理與幾何畫板構圖思維有機融合，揭示雙曲線與反比例函數的關系，讓情境圖形動起來，營造積極的互動體驗，提升了雙曲線學習效果．