基于Matlab的電阻爐溫度控制系統設計及仿真比較

夏百花，韋 穎，方 飛

（安徽三聯學院 電子電氣工程學院，安徽 合肥 230601）

電阻爐是熱處理工藝過程中應用最廣、數量最多的電加熱設備。隨著控制技術日新月異的發展，對電阻爐溫度控制的要求也就越來越高。電阻爐是利用電流通過電熱體元件將電能轉化為熱能來加熱或熔化工件和物料的熱加工設備，其溫度控制具有單向性、大慣性、大滯后等復雜特點，主要分為升溫、保溫和降溫3個部分，其中，升溫、保溫依賴電阻絲加熱完成，而降溫則主要依靠自然環境進行冷卻。

1 系統框架

電阻爐溫度控制系統多采用閉環控制，首先，將電阻爐實際溫度值通過溫度傳感器測量出來；其次，通過負反饋與設定溫度進行比較得到偏差信號，送入控制器中得到控制信號，控制可控硅，以此改變電阻絲的加熱電流或電壓，從而實現電阻爐的溫度控制[1]。系統框架如圖1所示。

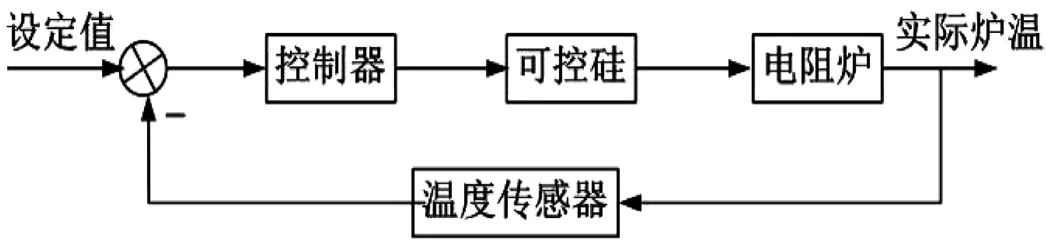
圖1 電阻爐溫度控制系統框架

本文主要是采用傳統PID控制、Smith控制和模糊控制3種算法實現對電阻爐溫度的控制，并進行仿真及對仿真結果的比較分析。

2 控制算法比較

理論分析和實驗結果表明，均將電阻爐當作具有自平衡能力且存有滯后的被控對象，因此其數學模型可用一階慣性和純滯后兩個環節進行描述，系統總的傳遞函數為：

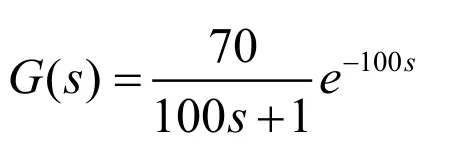
2.1 不加控制器仿真

不外加控制器的仿真模型控制如圖2所示，其仿真結果如圖3所示，可以看出，此系統具有100 ms的延遲，并且在仿真時間內僅上升到了70°左右（設定值為100°），且調節時間較長。

圖2 不加控制器的系統仿真模型

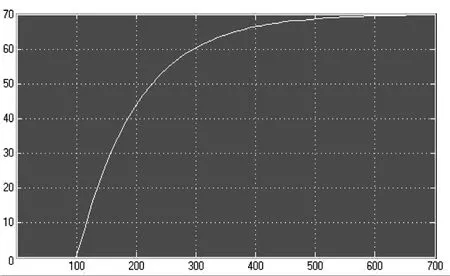
圖3 不加控制器的仿真結果

2.2 PID控制器仿真

PID控制器所采用的控制規律為比例、積分、微分控制，控制規律如圖4所示。

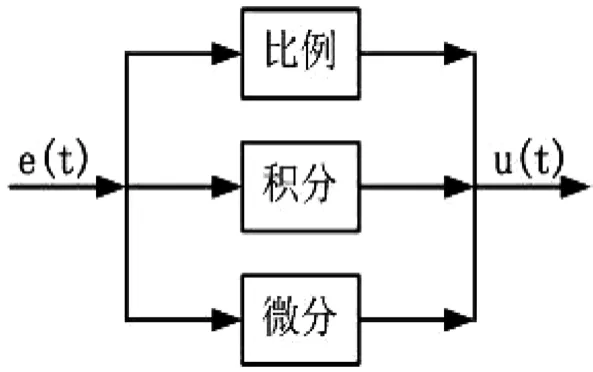
圖4 PID控制原理

其PID控制器的輸入與輸出之間的關系為：

對于此系統，在筆者有限的經驗范圍內，未找到使系統穩定的合適PID值。雖然PID控制器憑借結構簡單、參數調整方便等諸多優點應用于大多數控制系統中，但在此系統中延遲較大，難以實現對溫度的控制[2]。

2.3 Smith預估控制算法仿真

Smith預估控制算法是一種針對大時間滯后系統進行補償的常用方法。圖5為Kp=0.7，KI=0.16，Td=1.3時的Smith控制系統仿真結果。

可以看出，該控制方法超調量較大，動態過程調節時間較長。但在此系統中，當其溫度一旦出現超調量，就無法采用控制手段來降溫，因而應用傳統的控制理論和控制方法難以達到理想的控制效果[3]。

2.4 模糊控制算法仿真

智能控制方案是一類無需人為干預就能夠針對控制對象的狀態自動調節控制規律，以實現控制目標的控制策略。它和常規控制理論不同的地方在于：（1）不需要建立精確的數學模型。（2）不需要進行定量計算與困難性分析。它是一種無模型控制方案，即在不知道對象精確模型的情況下，在自我的調節作用下，使得實際響應曲線近似于理想響應曲線[4]。

模糊控制是智能控制的一個重要分支，本設計采用的模糊控制器采用兩輸入一輸出的控制方法，其中輸入為表示溫度誤差E和誤差變化率EC，輸出為控制加熱的供電電壓U，均為模糊變量。

此系統輸入為單位階躍信號，選取量化因子Ke=0.7，Kec=0.05，比例因子Ku=0.02，建立如圖6所示模糊控制系統，其Matlab仿真結果如圖7所示。可以得出，系統在整個響應過程中未出現超調現象，且動態調節時間減小。

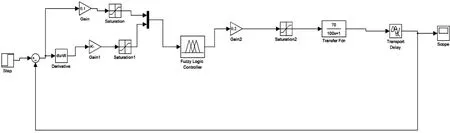
圖6 模糊控制系統仿真模型

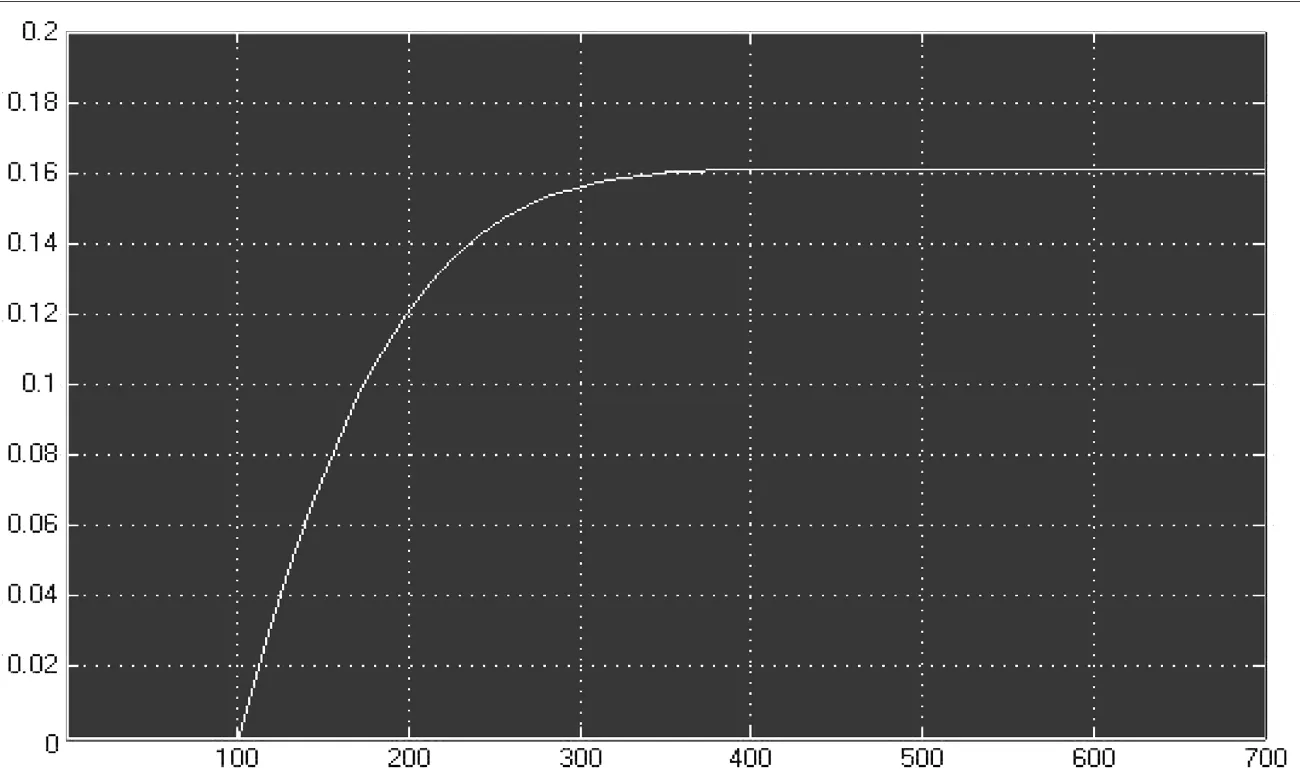
圖7 模糊控制系統仿真結果

3 結語

對于一個純滯后時間較長且不允許出現超調的電阻爐溫度控制來說，由于系統本身是一個自衡系統，雖能最終到達穩定狀態，但調節時間較長；而對于常規PID控制來說，比例、積分和微分3個參數不易找到，故不選用此算法；廣泛適用于滯后系統的Smith預估算法雖然也能穩定，但其算法中需要知道被控對象的準確數學模型，故不選用此方法；由于電阻爐本身結構較為復雜，其數學模型很難得到，當采用模糊控制時，整個系統的調節時間較小，且沒有出現超調現象，故選用此方法。