基于離散余弦變換的軸承故障診斷方法與應用研究

郭吉祥

(中鐵十一局集團漢江重工有限公司 湖北襄陽 441006)

1 引言

離散余弦變換(Discrete Cosine Transform，DCT)是和傅里葉變換相關的一種變換算法，經常在圖像處理和信號處理中使用。離散余弦變換的變換核函數為余弦函數，不但具有正交變換性質，而且它的變換矩陣基向量還能很好地表征圖像與信號的相關特征，因此常被認為是一種準最佳變換。近年來，已有不少學者將離散余弦變換算法應用到機械故障診斷領域，如尹麗[1]提出的采用離散余弦變換域循環維納濾波算法對振動信號進行濾波，不僅能保證線性相位，還具有良好的濾波效果；臧懷剛[2]等提出了一種基于改進的DCT和EMD的軸承故障診斷方法，能夠對軸承故障進行準確診斷；陳安華[3]等將離散余弦變換應用到列車輪對踏面損傷的檢測，可快速、準確地檢測出機車踏面的損傷，有效地提取列車輪對踏面損傷的特征信息；陳彥龍[4]等借助離散余弦變換(DCT)的頻域能量聚集性和奇異值分解(SVD)的時域能量聚集性，對軸承復合故障信號進行預處理，實現降噪并分離頻率相近的微弱故障信號；陳彥龍[5]等結合離散余弦變換(DCT)，將離散時間序列經過離散余弦變換處理成對應的系數向量，在閾值處理的基礎上，重構信號有效提取出了微弱故障信息；陳彥龍[6]等將振動信號進行離散余弦變換得到頻域系數，對頻域系數自動分段，并對不同分段情況下的頻域系數進行分析，克服了時域內相關分析受噪聲影響導致診斷不準確的缺點，在含噪聲情況下保證了診斷結果的穩定性、準確性；原菊梅[7]針對故障診斷特征參數的應用缺陷，提出了一種小波和余弦變換的感應電機軸承故障特征參數提取方法，并對實際感應電機軸承正常、內圈故障、外圈故障和滾珠故障的振動信號進行分析，有效地實現了電機軸承的早期故障檢測與診斷；楊麗娟[8]等提出一種適用于多軸承振動信號的分布式壓縮感知重構算法，通過引入離散余弦變換，實現了軸承振動信號在變換域的稀疏化和基于TSBL的重構算法，達到了多軸承振動信號聯合重構的目的，解決了軸承狀態監測中多傳感器數據采集造成的問題。

根據離散余弦變換的能量聚集性和線性性質，以及旋轉設備振動信號的循環平穩性，文獻[9-10]提出了利用多個數據包數據來設計濾波器以實現對信號消噪處理的方法。該種濾波器與其它經典濾波器主要不同在于此種濾波器完全由采集信號自身得到，而不需要事先指定頻域窗函數的形狀、幅值和位置，克服了傳統頻域濾波器的某些缺陷。本文借鑒其構造濾波器思想，設計了一種基于離散余弦變換的新型濾波器，基于此提出了離散余弦變換的軸承故障信號特征提取方法，并通過模擬信號和軸承故障信號兩個算例驗證該方法的有效性。

2 離散余弦變換原理

1974年，由N.Ahmed、T.Natarajan和 K.R.Rao提出離散余弦變換概念以來，很快在各種信號處理領域得到廣泛應用，其主要原因是離散余弦變換具有較好的能量集中特性。

假設給定一長度為N的序列x(n)，一維離散余弦變換和反變換由以下兩式定義:

由于離散余弦變換具有較好的能量集中特性，故信號中不同頻率特征的能量聚集分布在不同的頻帶，而噪聲信號則在整個頻帶中均勻分布。另外，離散余弦變換還具有線性特性，即使是噪聲污染的信號，其能量聚集特性也不會因此消失，且能很好地表征頻率特征的相關信息。

3 基于離散余弦變換的特征提取方法

3.1 構造離散余弦變換濾波器

由于離散余弦變換具有一個線性性質，即:DCT(x+y)＝DCT(x)+DCT(y)，本文基于此建立一個新濾波器。假設存在m組等長度信號zj(n)，由以下兩部分構成:

其中，y(n)為待處理的特征信號；wj(n)為噪聲信號。一般情況下，特征信號與噪聲信號互不相關。根據自相關函數的性質可知，周期性信號的自相關函數仍然是周期函數，且與原信號同周期，在采集各組信號zj(n)時，須保證各組信號中y(n)相位相同。該濾波器的構造過程如下:

(1)首先將zj(n)進行離散余弦變換，得到Fj(u)

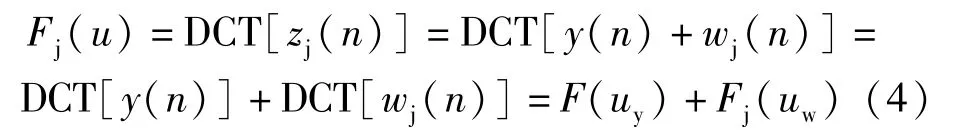
式中，F(uy)為特征信號頻域；Fj(uw)為噪聲信號頻域。

(2)構造濾波器

將上式中分子展開后得到:

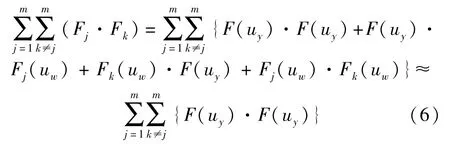
高斯白噪聲在時延為零時，具有最大的自相關值，自相關函數隨著時延m趨近無窮大時，則公式(6)中后三部分趨近于零，僅保留與y(n)中特征有關的部分。于是便得到一個略去絕大部分噪聲信號而保留下特征信號的窄帶新濾波器。由于構造的濾波器是頻域濾波器，任何一組周期信號的頻域是相同的，受噪聲影響后也近似相同，故可以任意選擇一組信號做為處理信號。

3.2 特征提取方法

從濾波器構造過程可以看出，采集的故障振動信號需保證得到多組等長度信號同相，這可以通過控制信號采集過程來解決。例如在旋轉機械平穩轉動過程中采集足夠長的信號，然后按照旋轉周期進行等長度分割來實現；對于非平穩信號可以在保證測量條件的前提下，通過重復多次測量便可得到所需采集的故障信號。

首先通過構造仿真或采集振動信號得到待提取信號，再將待處理信號根據需要等分多組，通過進行離散余弦變換得到特征信號頻域，然后根據本方法構造濾波器，進而可以從各組中任選一組離散余弦變換系數，與構造濾波器相乘，最后對所得的新離散余弦變換系數進行逆變換，從而得到去除絕大部分噪聲信號的特征信號。

基于離散余弦變換的特征提取方法具體步驟如下:

(1)將采集故障振動信號或仿真信號等分M組，或者重復多次測量M組故障振動信號；

(2)將M組故障振動信號進行DCT，并用于離散余弦變換系數構造濾波器H；

(3)從各組Fj(u)中任選一組離散余弦變換系數，與構造濾波器H相乘；

(4)將經過濾波器H處理后離散余弦變換系數進行IDCT，得到特征信號；

(5)最后通過提取的特征信號進行故障分析，確定故障類型。

4 模擬仿真信號

任選取一組平穩模擬仿真信號:

其中，w(t)為[-1 1]之間正態分布的隨機噪聲；系數k表征噪聲能量大小。

設定模擬仿真信號的采樣長度為20 s，采樣頻率為10 kHz，然后將設定模擬仿真信號等分100組，利用離散余弦變換理論及Matlab軟件構造濾波器，任選一組離散余弦變換系數，與構造濾波器H相乘后重構特征信號，即降噪信號。本文所用方法與小波變換降噪的結果進行對比，見圖1～圖4。其中圖1為無噪聲平穩信號時域圖與頻譜圖(即k＝0)；圖2為含強噪聲的平穩信號時域圖與頻譜圖(k＝15)；圖3、圖4分別為小波變換和本文方法降噪后的時域圖與頻譜圖。

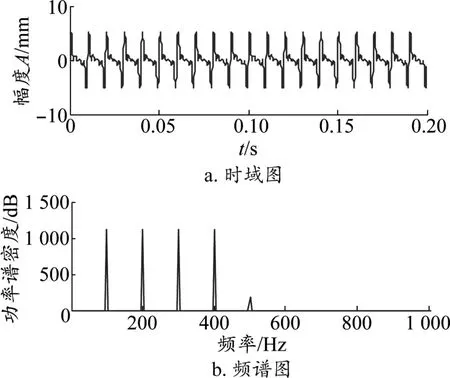
圖1 無噪聲信號時域圖與頻譜圖

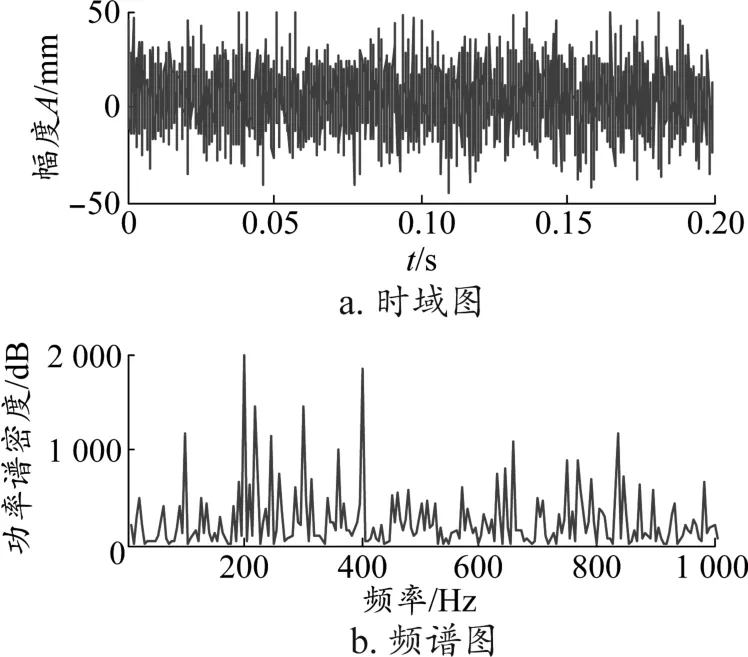
圖2 k＝15時信號時域圖與頻譜圖

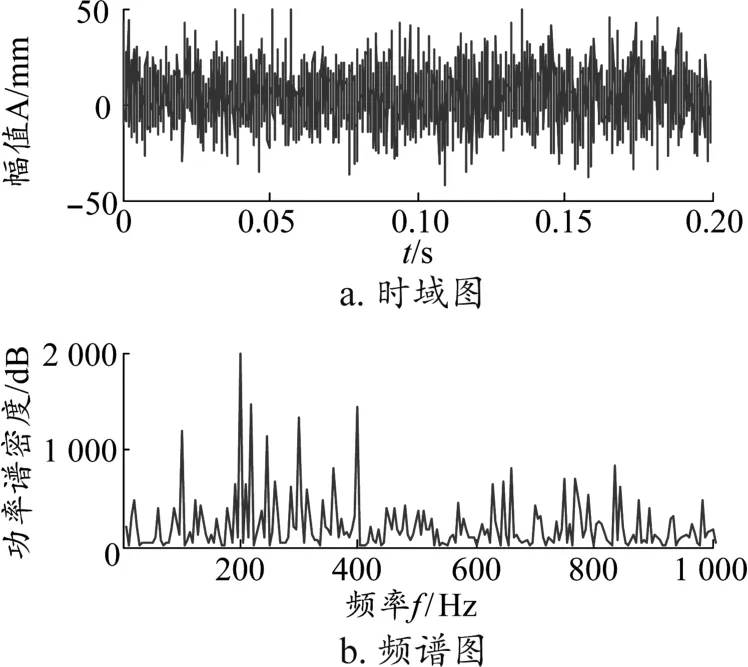
圖3 k＝15時小波降噪信號時域圖與頻譜圖

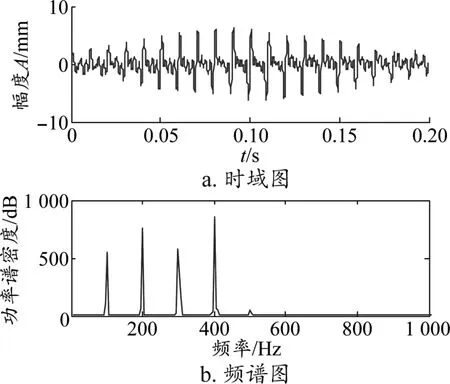
圖4 k＝15時本方法降噪信號時域圖與頻譜圖

從圖2～圖4可知，當噪聲相對較強時，小波變換降噪的時域圖與模擬仿真信號時域圖相比，分辨不出信號的波形；而本文降噪信號時域圖與模擬仿真信號時域圖相比可以看出，本文方法能夠清晰看出信號的波形，真正實現降噪目的。在頻域圖中，小波變換降噪與模擬仿真信號頻域圖相比，同樣不能提取出特征信號；而本文方法與小波變換降噪效果相比，能夠非常有效地提取模擬仿真信號的特征峰值，且能準確分析出模擬仿真信號設定的特征頻率。由于噪聲雜亂無章，隨著噪聲信號能量的增大，一定程度上抵消了周期信號的能量，故在模擬仿真信號進行降噪后，其時域圖與頻域圖里表現出的幅值則相應減小，再加上濾波處理，也在一定程度上減小了特征信號的幅值。

5 實測軸承故障信號分析

為進一步驗證本文方法的有效性，采用旋轉機械振動分析及故障診斷試驗平臺系統，采集滾動軸承外圈故障的振動信號。試驗中采用軸承型號為N205EM，滾柱個數為13，滾柱直徑為7.5 mm，滾道節徑為38.5 mm，轉速為867 r/min；采樣頻率為20 kHz，采樣點數為32 768，計算得到軸承外圈特征頻率為75.6 Hz，軸頻為14.45 Hz。重復采集16組數據進行分析，所得故障信號時域圖與頻譜圖、小波降噪信號時域圖與頻譜圖、本方法降噪信號時域圖與頻譜圖見圖5～圖7。

圖5 故障信號時域圖與頻譜圖

圖6 小波降噪信號時域圖與頻譜圖

圖7 本方法降噪信號時域圖與頻譜圖

分析圖5～圖7可知，本文方法降噪后信號的時域波形與實測軸承故障信號、小波降噪后信號的時域波形相比，其噪聲能量明顯減弱；從實測軸承故障信號、小波降噪的頻譜圖可發現，雖然都能在軸承外圈故障特征頻率(75.6 Hz)及2倍頻、3倍頻處找出故障頻率峰值，但仍不能完全確定是否存在有調制現象，而在本文方法降噪后的頻譜圖中不僅能夠發現在軸承外圈故障特征頻率(75.6 Hz)及2倍頻、3倍頻處存在較為清晰的頻率峰值，而且還能確定在這些故障特征頻率處不存在調制譜線，根據上述故障頻率特征便能判斷軸承外圈存在故障。

6 結論

本文利用離散余弦變換的能量聚集特性和線性特性及旋轉設備振動信號的循環平穩性，提出了一種基于離散余弦變換的軸承故障診斷方法。通過文中模擬仿真和故障信號兩個例子可見，本文方法濾波器的形狀、幅值、位置等完全由采集信號自身確定。

通過對上述仿真信號和故障信號降噪效果分析，本文方法與小波降噪方法相比，具有良好的消噪效果，能很好地抑制信號中各頻段的噪聲分量，避免了一些小能量的平穩或循環平穩分量當作噪聲消除的缺點，更能有效地提取軸承故障信號的時頻特征，為軸承故障診斷提供技術支持，有望應用到相關領域中。