基于響應面法和重要性抽樣的桿塔掏挖基礎抗拔可靠性分析

周佳成 丁士君 李鏡培，* 楊文智

（1.同濟大學地下建筑與工程系，上海200092；2.北京工業大學建筑工程學院，北京100124；3.中國電力科學研究院有限公司，北京100055）

0 引 言

桿塔掏挖基礎是利用機械或人工在天然土中直接挖（鉆）成所需要的基坑，將鋼筋骨架和混凝土直接澆注于基坑內而成型的桿塔基礎，如圖1所示。桿塔掏挖基礎由于棄土棄渣少、水土流失量少、對環境影響小等優點被廣泛應用于山區丘陵中地質條件較好的地區。

桿塔基礎作為輸電桿塔的直接支撐，其可靠性直接關系到整個輸電線路的安全，但現行的桿塔基礎設計規范只是將工民建規范中的分項系數直接套用過來，未作系統的分析工作［1］。實際上桿塔基礎的控制工況多為上拔工況，而工民建基礎的控制工況多為下壓工況；此外，前者是由活載起控制作用，而后者通常是由恒載起控制作用，這表現在前者的荷載效應比ρ（活載效應標準值/恒載效應標準值）為3.3～8.3［2］，后者的荷載效應比為0.2～1。因此，直接套用工民建規范是不合適的。

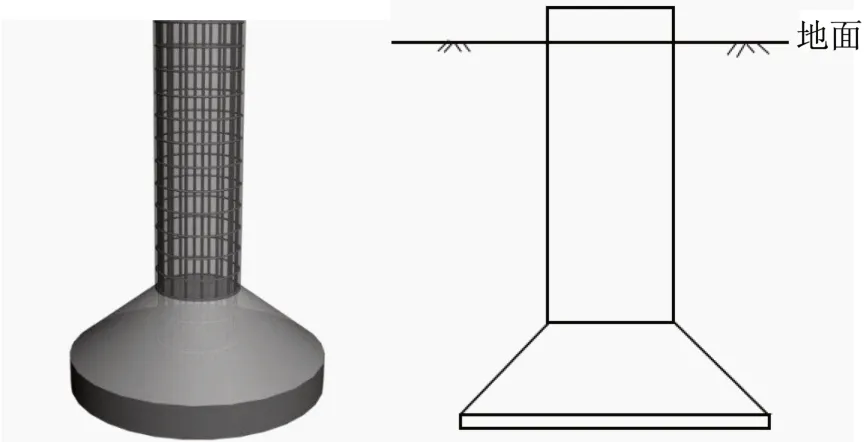
圖1 掏挖基礎模型及剖面圖Fig.1 Model and section of excavated foundation

國際上對桿塔基礎可靠性的研究可追溯至上世紀九十年代，且已形成較為系統的分項系數設計 法 。 DiGioia 和 Rojas-Gonzalez［3-4］基 于 RBD 法（Reliability-Based Design）分析了桿塔基礎的可靠性，得到了總荷載分項系數和總抗力分項系數。Phoon 等［5-7］結合輸電線路基礎的特性，基于校準法提出了多分項系數設計法。我國對于桿塔基礎可靠性研究起步較晚，相關研究成果較少，魯先龍等［8-9］、徐彬等［10］、張子富等［11］做了一些有益的嘗試，但仍不能滿足分項系數設計法的需要。由于國內掏挖基礎可靠性研究成果較少，本文借鑒了巖土工程中擴展式淺基礎可靠性的研究方法。謝妍等［12］考慮了承載力極限狀態和正常使用極限狀態下淺基礎的可靠性問題，分析了各影響因素的敏感性；邵克博等［13］基于子集模擬提出了一種淺基礎擴展可靠性研究方法，同時編制了相應的計算程序；張亞楠等［14］采用方差折減法對擴展式淺基礎可靠性進行了研究，得到的結果偏保守。翟明洋［15］采用隨機響應面法分析了三層巖土邊坡和含軟弱結構面巖質邊坡穩定可靠度問題；程曄等［16］研究了響應面法和重要性抽樣法在巖土工程可靠性分析中的應用；姚貝貝等［17］基于響應面法和重要性抽樣法對隧道襯砌的時變可靠度進行了研究。

當考慮巖土參數的變異性時，桿塔基礎抗拔極限承載力限狀態方程是極其復雜且高度非線性的，為此本文采用二次響應面法（RSM）和重要性抽樣（IS）方法進行可靠度分析。近幾年，這兩種方法作為一種組合得到了越來越多的應用，響應面法計算簡單，而重要性抽樣法效率較高且結果精確，兩者相結合對可靠性問題的分析研究將更加全面準確和快速高效。

1 剪切法抗拔極限狀態方程

對于原狀土基礎而言，其抗拔承載力可按照《架空輸電線路基礎設計技術規程》（DL/T 5219—2014）［18］中的“剪切法”進行計算。

1.1 剪切法抗拔極限承載力

本文考慮淺基礎破壞情形（基礎埋深ht≤抗拔臨界深度hc），計算簡圖如圖2 所示，圓弧滑動面形狀參數與基礎深徑比λ（基礎深度ht/基底直徑D）和土的性質有關。抗拔承載力由三部分組成：基礎自重Gf、圓弧滑動面以上土的重度Gs和圓弧滑動面上剪應力的豎向分量Tv。

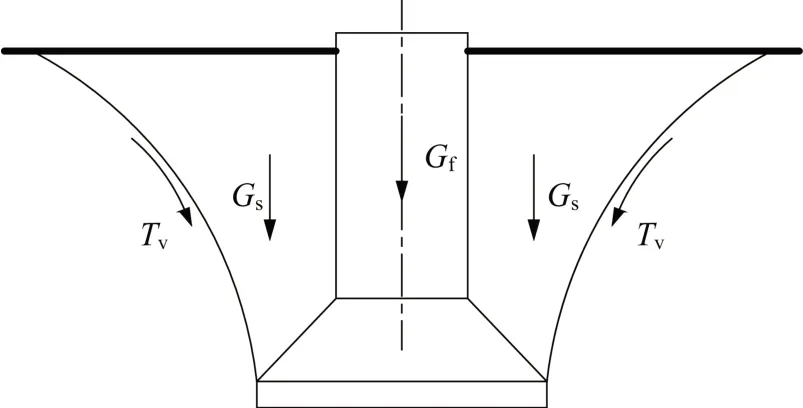
圖2 剪切法計算上拔承載力Fig.2 Calculation of uplift bearing capacity by shearing method

從而按剪切法確定的掏挖基礎極限抗拔承載力理論值為

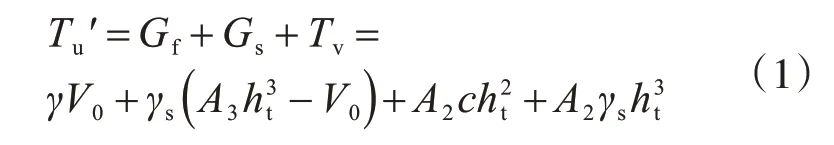
式中：γ，V0分別為基礎重度和體積；γs，c分別為土的加權平均重度和加權平均黏聚力；A1，A2，A3為無因次計算參數，與滑動面形狀參數、內摩擦角φ和基礎深徑比λ有關，具體公式較冗長，可參考文獻［18］附錄D，限于篇幅此處不作展開。

需要指出的是，抗拔極限承載力受到水平力和基底擴展角影響，因此文獻［18］給出了水平力影響系數γE和基底擴展角影響系數γθ。此外，剪切法計算值和原位試驗值仍存在差異，故采用試計比λT（計算值/試驗值）來考慮計算模式的不確定性。綜合上述因素，掏挖基礎極限抗拔承載力修正值為

1.2 剪切法抗拔極限狀態方程

極限狀態方程的一般形式為

式中：R為抗力效應，對于本文研究的問題而言即為式（2）；S為荷載效應，可分為恒載效應和活載效應。

桿塔結構所受的活載有風荷載、覆冰荷載、導線張力荷載等，傳遞到基礎上的活載效應也是這幾種活載導致的。根據線路運行實際經驗和桿塔設計要求，在線路運行的某一時刻，一般只有一種活載起控制作用。而桿塔多屬于高聳結構，特別是近幾年發展起來的特高壓輸電桿塔，大風荷載是最主要的活載［19］。因此本文基于“恒載SG+風載SW”這一荷載效應組合，建立如下極限狀態方程：

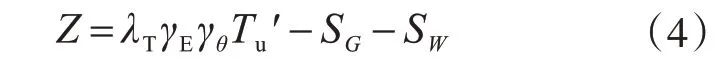
式（4）中所有參數可分為四類：

第一類是基礎參數，包括基礎重度γ、基礎體積V0、基礎埋深ht、基底直徑D、深徑比λ，這些變量變異性很小，可視為常量。

第二類是巖土參數，包括土重度γs和抗剪指標c，φ，由于土重度γs變異性較小，僅將c，φ視為隨機變量。

第三類是荷載參數，包括恒載效應SG、風載效應SW，均視為隨機變量。

第四類無量綱參數，包括λT，γE，γθ，A1，A2，A3。對于特定的工程問題，γE，γθ為常量；A1，A2，A3與基礎參數和內摩擦角φ有關，其中基礎參數為常量，從而A1，A2，A3的變異性是由φ的變異性造成的，故不將A1，A2，A3視為新變量；試計比λT表征計算模式的不確定性，視為隨機變量。

綜上，式（4）中共有5 個基本隨機變量，分別為試計比λT，抗剪指標c，φ，荷載效應SG，SW。

2 基本隨機變量的統計特性

在進行可靠性分析之前，需要研究基本隨機變量的統計特性，下文將逐一給出式（4）中基本變量的統計參數。

2.1 試計比λT

魯先龍等［9］通過分析大量的掏挖基礎抗拔試驗數據，得到試計比λT服從對數正態分布，其統計參數因土性而異，詳見表1。

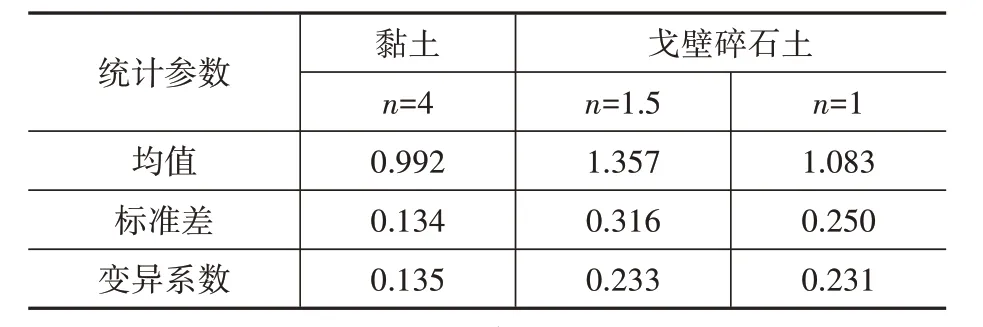
表1 λT的統計參數［9］Table 1 Statistical parameter of λT

2.2 荷載效應SG，SW

根據《建筑結構設計統一標準》（GBJ 68—84）［20］，恒載G服從正態分布，風載服從極值 I 型分布，相應的統計參數見表2，表中GK，WK為恒載和風載的標準值。

將荷載與荷載效應近似按線性關系考慮，從而恒載效應SG服從正態分布，均值為1.060SGK，變異系數為0.070；風載效應SW服從極值I 型分布，均值為 1.109SWK，變異系數為 0.193。SGK，SWK為恒載效應和風載效應的標準值，根據工程實際情況按照相應的規范計算得到。

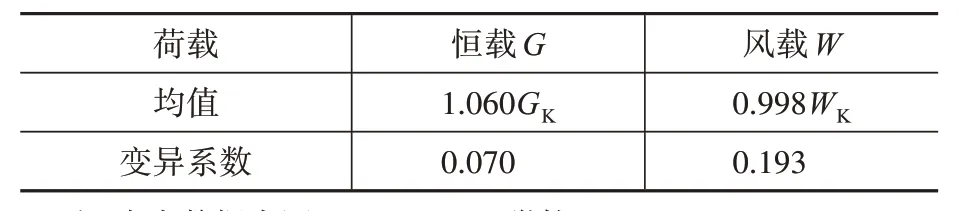
表2 荷載統計參數Table 2 Statistical parameters of the load

2.3 抗剪指標c,φ

抗剪強度指標具有自相關性和互相關性，描述自相關性可采用Vanmarcke［21-22］提出的隨機場模型，描述互相關性則可利用互相關系數［23］。

1）自相關性

隨機場局部平均理論是描述巖土參數自相關性的常用手段。對于抗剪指標c，φ，可認為其在水平方向一定范圍內變化不大，而沿深度方向變化較大［25］，因此可以用一維隨機場來描述其空間變異性。以黏聚力c為例，它在深度方向的空間均值為

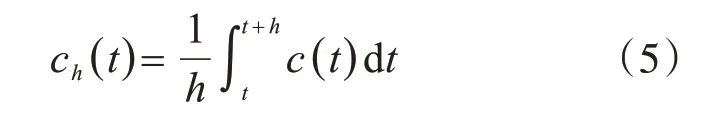
式中：ch(t)還可以理解為黏聚力加權平均值，這與式（4）中基本變量c的含義一致；t為計算起始位置；h為計算深度；c(t)是計算深度范圍內各點的黏聚力，為一維平穩隨機場。

對于特定的工程問題，它們都是確定的，因此ch(t)為一隨機變量，它的均值和方差為

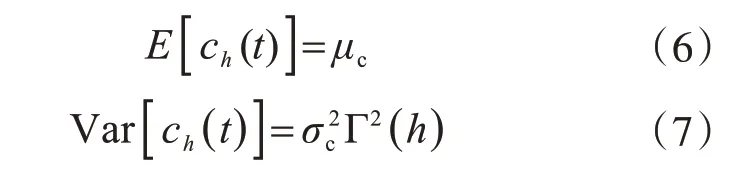
式中，μc，σc為點均值和點方差；Γ2(h)為方差折減系數，Vanmarcke［21］建議按下式確定：

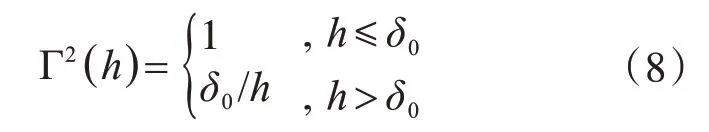
式中，δ0為相關距離。

以上分析是對于單一的或性質相近的土層而言。對于多層土，設土層數為n，相應土層編號為1，2，…，n。對于土層i(i≤n)，相關距離為δ0i，一般δ0i＜hi；黏聚力空間均值為chi(t)，由式（6）、式（7）求得其均值和方差分別為μi，σi2δ0i/hi，字母含義與上文一致。則n層土黏聚力的加權平均值為

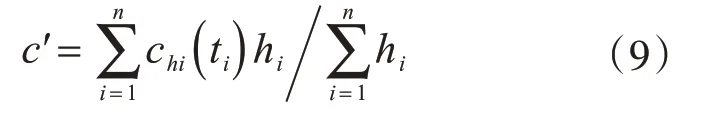
方便起見，將c′稱為計算黏聚力，其意義與式（4）中基本變量c一致。同理，c′仍為隨機變量，其均值和方差為

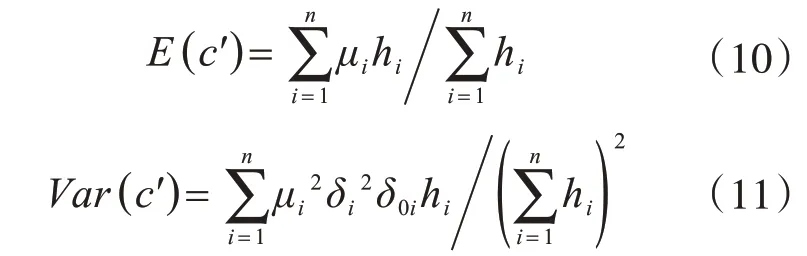
Lacasse 等［26］和李鏡培等［27］的研究表明，c，φ均服從正態分布，因此式（5）中c(t)為一維平穩正態隨機場，由數理統計理論，計算黏聚力c′也服從正態分布。從而在得到抗剪指標的點概率特性后，由式（5）-式（11），便得式（4）中基本變量概率c，φ概率特性。

2）互相關性

抗剪指標c，φ存在較強的互相關性，其相關系數多在-0.6～-0.8 之間［24］。雖然這里的相關系數是針對某一點的統計特性而言，嚴格上與計算抗剪指標c′，φ′的相關系數并不一致。但計算兩個隨機場之間的互相關系數較為復雜，為簡便起見，認為這兩者的相關系數是相同的。

3 響應面法

響應面法（RSM）是通過構造一個曲面來模擬真實曲面，該曲面稱為響應面，按精度可分為一次響應面法和二次響應面法，后者精度高于前者。一次響應面法是采用平面模擬極限狀態曲面，二次響應面法采用二次曲面模擬極限狀態曲面。

為減少抽樣樣本點個數，在應用二次響應面法采用標準型形式，即

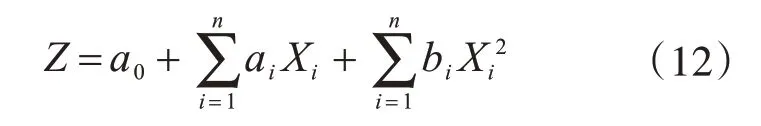
式中，Xi為基本變量；n為基本變量個數；a0，ai，bi為待定參數，共2n+1 個，因此需要2n+1 個抽樣點。

目前應用較多的抽樣方法是中心復合抽樣，具體做法為：先選定抽樣中心點坐標(x1，…，xi，…，xn)，然 后 按 (x1，…，xi±fσi，…，xn)選取 2n個點。其中，σi為基本變量Xi的標準差；f為抽樣參數。理想的抽樣中心點應該是驗算點，但事先驗算點并不清楚，因此需要迭代計算。f在第一次迭代時可取2n/4，在之后迭代中取前一次的平方根。

將抽樣點坐標代入功能函數，便可得到2n+1個功能函數值，聯立式（13）便可求得待定參數，從而得到功能函數的簡單顯示表達式，然后結合JC法求解。由于不論是中心復合抽樣還是JC 法都要涉及大量的迭代，本文采用自行編制的MATLAB程序計算，具體的迭代過程如下：

（1）確定第1 次抽樣的中心點坐標x(1)，可取均值點

（2）計算抽樣參數f值，按中心復合抽樣法抽取2n+1個樣本點。

（3）將樣本點代入功能函數Z=g(x)，得到2n+1 個函數值，聯立式（13）求得待定參數，得到功能函數的簡單顯示表達式Z=G(x)。

（4）利用JC 法求解可靠度指標β()k和驗算點坐標x*(k)，該法較為常見，限于篇幅，迭代過程不作展開。

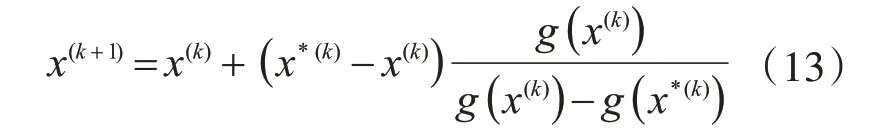
這樣取點是為了包含更多原極限狀態面的信息。

（6）重復步驟（2）-（5），直至滿足收斂條件。

4 重要性抽樣(IS)

蒙特卡羅法在可靠性分析中應用極廣，常用來檢驗其他可靠度計算方法的精度。它基于大數定律，首先產生基本變量的隨機樣本，然后代入功能函數，再統計失效區功能函數的數量，從而估計失效概率的一種方法。對于常規的工程問題，Ma［26］建議抽樣次數取

式中，Pf為預估的失效概率，或為其他可靠度計算方法得到的失效概率。

本文通過響應面法試算得到掏挖基礎抗拔失效概率約為10-5，由式（20）可知至少要進行107次抽樣方能滿足常規工程需要，而這往往是很難實現的，為此本文采用重要性抽樣技巧。

Shinozuka［27］是最早將重要性抽樣引入到可靠度計算的學者之一，其基本思想是：構造新的抽樣函數p(X)代替原抽樣函數f(X)，從而改變抽樣中心，使樣本點有較多機會落入失效區，增加功能函數Z＜0的機會，提高抽樣效率。p(X)的構造方法有很多，理想的p(X)應該與|f(X)|呈正比，但這往往是難以實現的。為簡單起見，本文采用Harbitz［28］提出的中心正態抽樣法：選擇n維正態分布密度函數作為抽樣函數，將抽樣中心放在驗算點處，即以驗算點和原基本變量的方差作為抽樣函數的均值和方差，這是應用最多的重要性抽樣方法之一。

5 算例

某懸垂型混凝土桿塔基礎，如圖3 所示，基礎參數如下：埋深3 m；主柱高度2 m，直徑1 m，露頭0.2 m；圓臺高度1 m，基底展開角為45°；底板直徑3 m，厚度0.2 m。

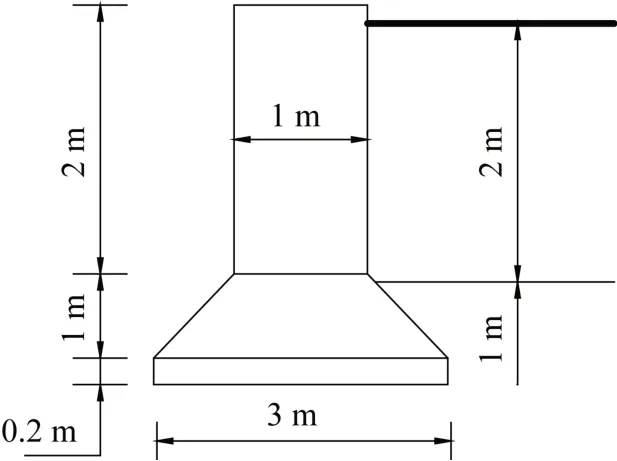
圖3 計算簡圖Fig.3 Calculation diagram

土層參數如下：基礎埋深范圍內為兩層硬塑黏土，自上而下記為土層1、土層2，土層1厚度2 m，土層2厚度5 m，無地下水和軟弱下臥層。兩層黏土的抗剪指標統計參數見表3，相關系數為-0.7。

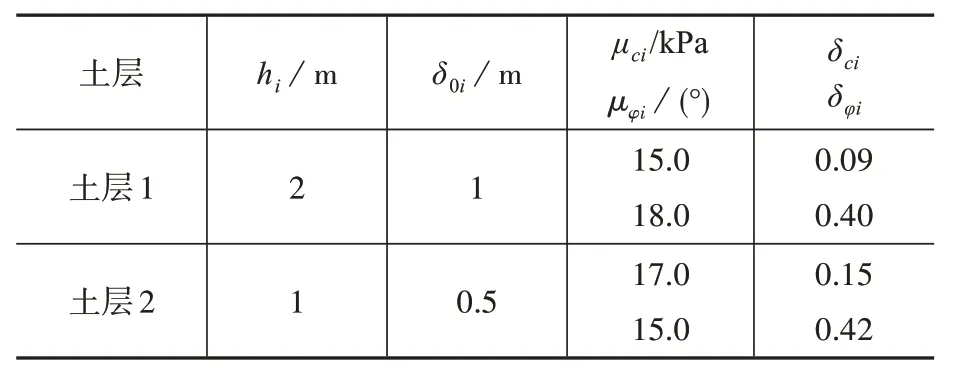
表3 抗剪指標的統計參數Table 3 Statistical parameters of shear index

5個基本變量統計參數的確定方法如下：

（1）基本變量λT：根據表1選取（黏土）；

（2）基本變量c，φ：根據表3 和隨機場理論求解其均值和變異系數，同時取相關系數為-0.7；

（3）基本變量SG，SW：結合算例條件，選取合適的SG，SW。

綜上，得到5 個基本變量的統計參數，見表4。

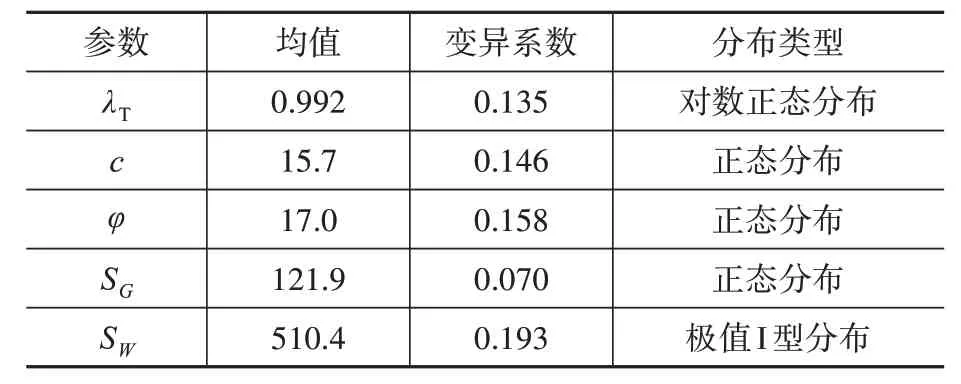
表4 基本變量的統計參數Table 4 Statistical parameters of basic variable

采用自行編制的二次響應面法MATLAB 程序對算例進行計算，收斂精度取ε=10-3。經過6次迭代，二次響應面法收斂，得到可靠度指標β=3.866 5，迭代過程見表5。

由表5 可知，二次響應面法迭代收斂得很快，可見其在桿塔掏挖基礎抗拔可靠性分析中的優勢。將最終的驗算點坐標代入重要性抽樣MATLAB 程序，求解可靠度指標以及相應的變異系數。需要指出的是，對相同抽樣次數進行多次試驗，可靠度指標和變異系數計算結果并不相同，這是由重要性抽樣自身的變異性和用p^f代替pf求解變異系數導致的。為此，本文對各種抽樣次數分別進行了20 次獨立試驗，取平均值作為該抽樣次數下的代表值，并計算了與響應面法計算結果的相對誤差，詳見表6。

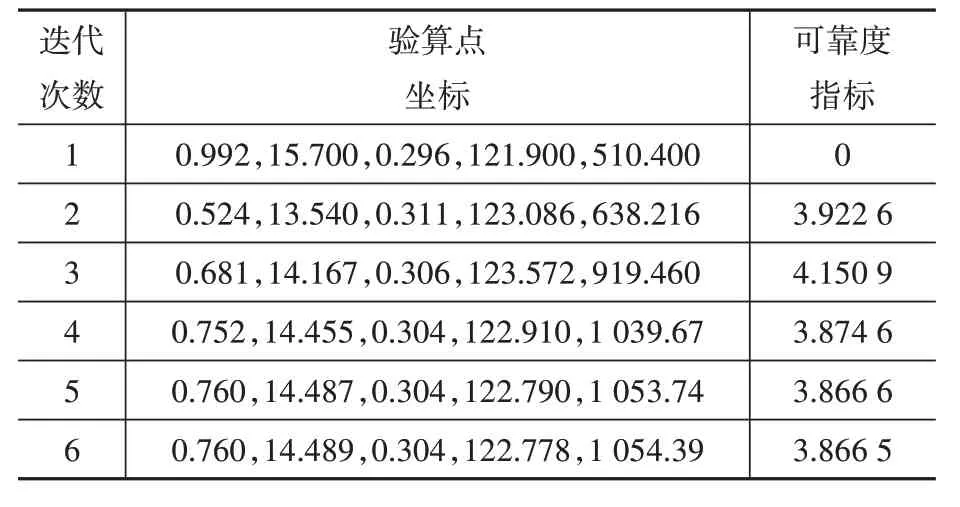
表5 響應面法的迭代過程Table 5 Iteration process of RSM

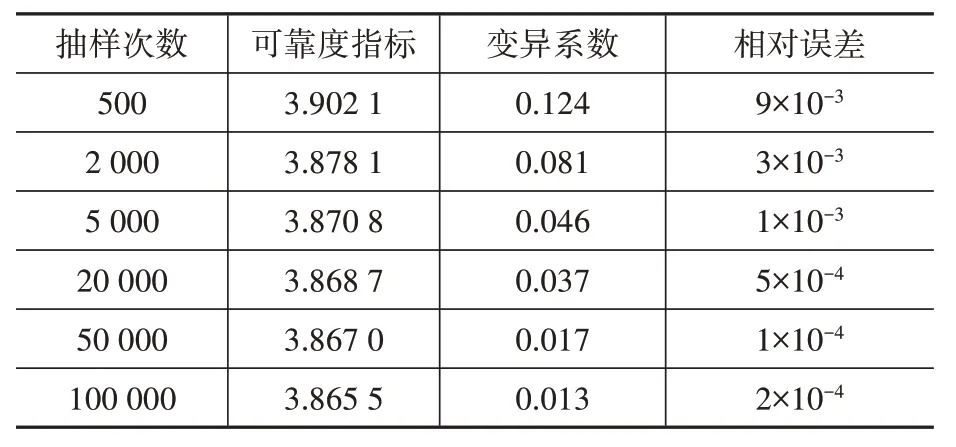
表6 重要性抽樣的計算結果Table 6 Calculation results of IS

由表6計算結果可得出以下幾點結論：

（1）響應面法的計算結果與精確解相當。當抽樣次數達到100 000次時，重要性抽樣的變異系數僅為0.013，因此可認為此時的可靠度指標3.865 5 為精確解。與響應面法的計算結果相比，相對誤差只有2×10-4，這對于工程問題已經相當精確。

（2）重要性抽樣的效率顯著。本例的失效概率約為10-5，若采用常規蒙特卡羅方法，由式（19）可知，達到變異系數為0.1 這一精度需要模擬107次；而達到變異系數為0.01 這一精度則需要模擬109次。相比之下，重要性抽樣只需模擬約106次便可達到變異系數為0.01這一精度。

（3）采用中心正態抽樣法是可行的。由于多維正態分布函數并不是最優的抽樣函數，可能會影響到重要性抽樣的抽樣效率。由表6 可知，當抽樣次數僅為500 次時，其可靠度指標計算值與精確解只差約1%，效率并不差。

6 抗拔基礎可靠性影響因素分析

基本變量的變異性、荷載效應比及安全系數對桿塔掏挖基礎的可靠度指標均有影響，下文將分別研究。

6.1 可靠度指標與基本變量的變異性

式（4）中，試計比λT和荷載效應SG，SW的變異系數是確定的，而抗剪指標c，φ對于不同的場地變異性有差異。為此，仍以上述算例為背景，分別改變c，φ變異系數，使其在0.1～0.45 變化，分析可靠度指標的變化情況，詳見圖4。

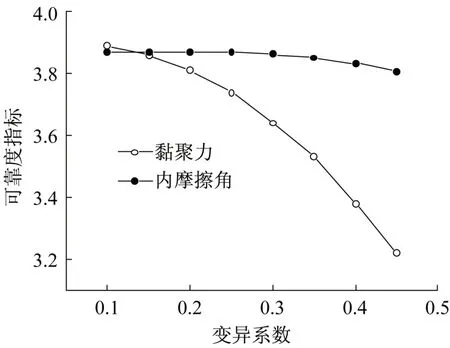
圖4 抗剪指標的敏感性Fig.4 Sensitivity of shear indicators

由圖4 可知，隨著抗剪指標變異系數的增加，可靠度指標減小，并且c的敏感性顯著大于φ的敏感性。因此在工程勘察時，需要重點關注黏聚力變異系數的正確性，防止其對可靠度指標造成較大影響。

6.2 可靠度指標與荷載效應比

前面提及可靠度指標β與荷載效應比ρ有關，桿塔基礎的荷載效應比范圍為3.3～8.3。仍以算例為背景，保證其他基本變量的統計特性均不變，僅改變荷載效應比，由文獻［18］的設計方法反算出荷載效應SG，SW，見表7，這樣可以分析當前規范的可靠度水準。

利用二次響應面法計算可靠度指標，結果見圖5。由圖5 可知，一方面，隨著荷載效應比的增加，可靠度指標降低，這是活載的變異系數大于恒載的變異系數導致的；另一方面，隨著荷載效應比的增加，可靠度指標減小的趨勢變緩，可以預測，隨著荷載效應比的逐漸增大，可靠度指標將趨于穩定。

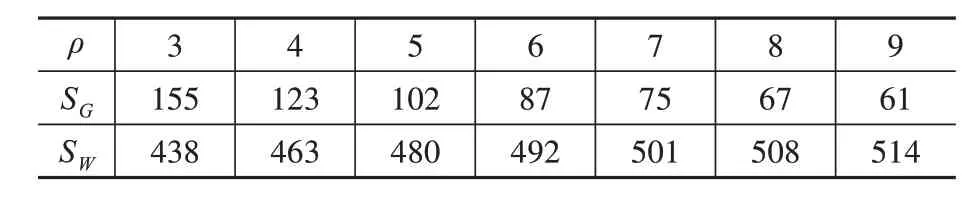
表7 不同荷載效應比條件下的荷載效應Table 7 Load effect under different load effect ratios

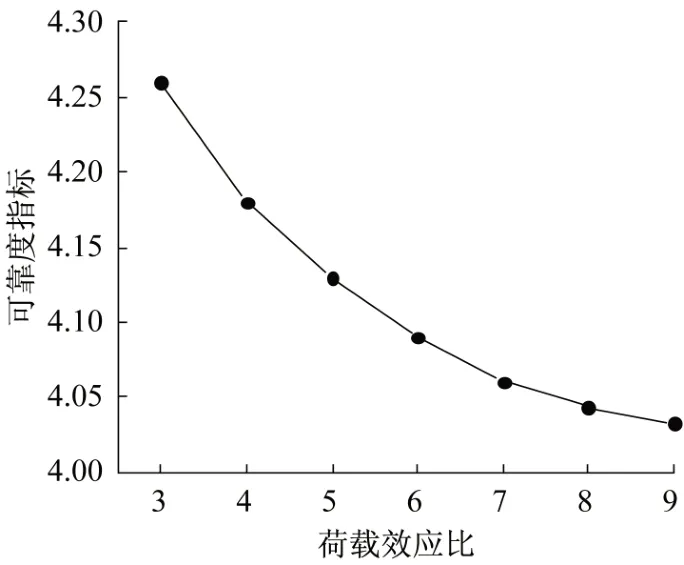
圖5 不同荷載效應比條件下的可靠度指標Fig.5 Reliability index under different load effect ratio conditions

6.3 可靠度指標與安全系數

文獻［18］雖然采用以基于概率理論的分項系數設計法，但由其條文說明3.0.16 可以看出，其中基礎附加分項系數γf是按照《架空輸電線路設計技術規程》（SDJ 3—1979）換算的，并未做系統的可靠度分析工作。魯先龍［9］在修訂文獻［18］時，比較了安全系數設計法與分項系數設計法的聯系，給出了安全系數與分項系數的關系式：

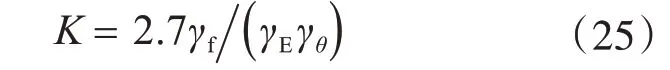
式中，γf為基礎附加分項系數，其余字母含義與上文一致。γf，γE，γθ的取值和桿塔類型、水平力與上拔力比值以及基底擴展角有關，由文獻［18］得到不同工況下安全系數，見表8。

由表8 可知，安全系數的最小值為2.48，最大值為5.76。考慮到γE的取值范圍為0.75～1，故可研究安全系數在2.3～5.8 之間變化時可靠度指標的變化情況。為此，仍以本算例為依據，將安全系數每次增加0.5，保持基本變量λT，c，φ統計參數以及荷載效應比ρ=4 不變，結合文獻［18］反算出SG，SW，見表9。

此外，γθ與γf，γE的不同之處在于，γf，γE的取值不會影響其他基本變量取值，但γθ的取值取決于基底展開角，基底展開角與一些計算參數如基底直徑，基礎體積存在關系。為此，算例中特意取基底展開角為臨界值45°，此時γθ=1；若要考慮γθ=1.2 的情況，只需將基底展開角增大很小的角度，如變為46°，這對基礎尺寸的影響是微小的，仍可按照原基礎尺寸進行計算，從而減少了不必要的麻煩。計算結果見圖6。

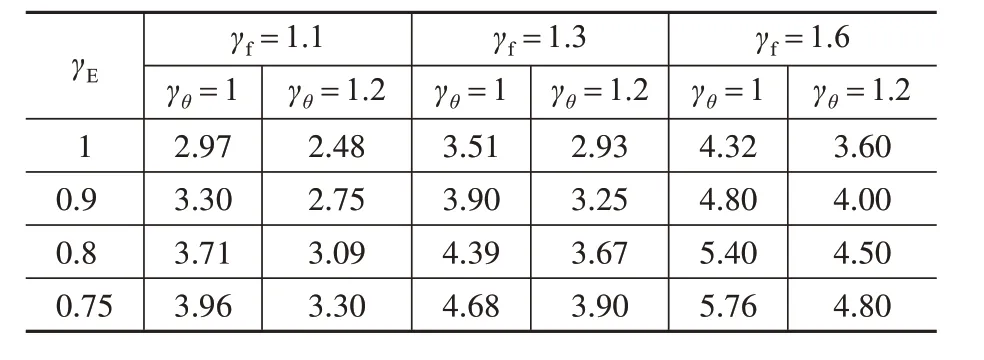
表8 不同工況下剪切法的安全系數Table 8 Safety factor of shearing method under different working conditions

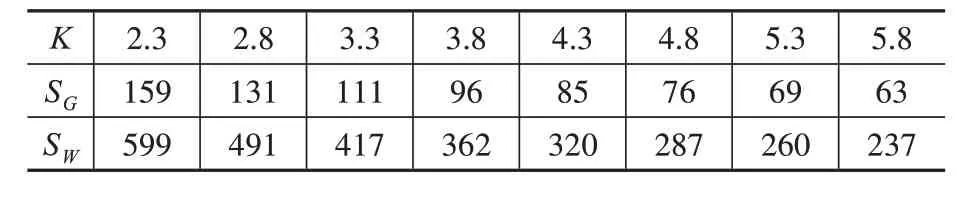
表9 不同安全系數下的荷載效應Table 9 Load effect under different safety factors

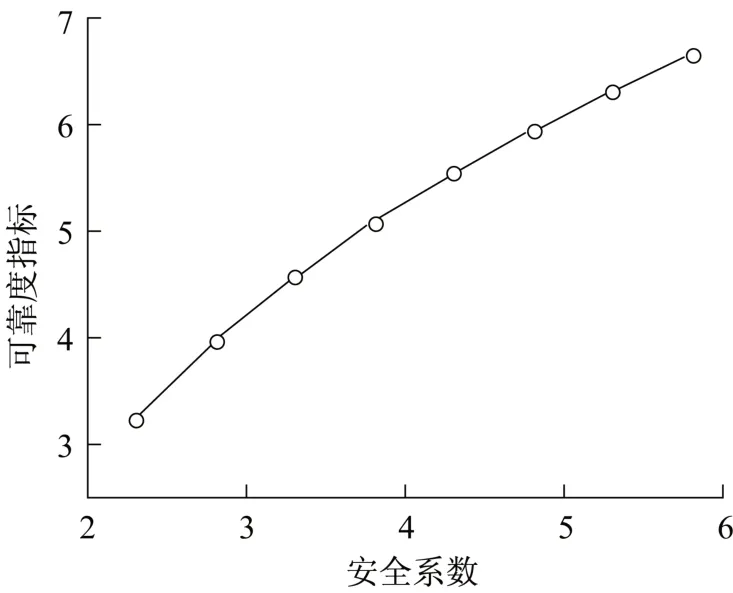
圖6 不同安全系數下的可靠度指標Fig.6 Reliability index under different safety factors

由圖6 可知，桿塔基礎可靠度指標隨安全系數增大而增大，大致呈線性變化。上述不同工況的可靠度指標平均值為5.17，遠大于二級脆性結構的可靠度指標3.7。因此輸電線路原狀土掏挖基礎的抗拔可靠度水準遠高于上部結構，這就從理論上揭示了除泥石流、沖刷、塌陷等自然災害外，我國桿塔基礎發生工程事故較少的原因。

7 結 論

本文基于剪切法建立了原狀土桿塔基礎抗拔承載力極限狀態方程，采用二次響應面法求解了可靠度指標并分析了其影響因素，并用重要性抽樣法驗證了響應面法的合理性。主要得到以下幾點結論：

（1）采用二次響應面法分析桿塔基礎抗拔可靠性是合適的，其計算精度與重要性抽樣法相當。

（2）桿塔基礎抗拔可靠性對黏聚力較為敏感，對內摩擦角的敏感性一般；隨著荷載效應比的增加，可靠度指標逐漸減小并有趨于穩定的趨勢；可靠度指標隨著安全系數的增大而增大，呈近似線性關系。

（3）桿塔基礎抗拔可靠度水準遠大于上部結構的可靠度水準，這也解釋了桿塔基礎失效較少的原因。