管內(nèi)水流和地鐵振動(dòng)耦合作用下埋地供水管道的振動(dòng)響應(yīng)分析

李顯昌 朱海濤 ，2，*

（1.天津大學(xué)建筑工程學(xué)院土木工程系，天津300072；2.濱海土木工程結(jié)構(gòu)與安全教育部重點(diǎn)實(shí)驗(yàn)室（天津大學(xué)），天津300072）

0 引 言

供水管道作為城市的“生命線”，其一旦遭到破壞將嚴(yán)重影響城市的正常運(yùn)轉(zhuǎn)，甚至危害市民的生命安全。埋地供水管道運(yùn)行環(huán)境十分復(fù)雜，誘發(fā)管道事故的因素很多，例如斷層、不均勻沉降、震害、溫度、腐蝕、老化等［1］。隨著近些年地鐵的大規(guī)模建設(shè)，地下空間變得日益狹窄，隧道和管線交叉鄰近現(xiàn)象也日愈常見。地鐵在運(yùn)行過程中產(chǎn)生振動(dòng)，振動(dòng)以波的形式通過道床傳遞給隧道支護(hù)，支護(hù)結(jié)構(gòu)再通過周圍巖土介質(zhì)向外傳播，進(jìn)而誘發(fā)埋地供水管道振動(dòng)，對其運(yùn)行安全造成影響［2-3］。

實(shí)事上，類似問題已經(jīng)引起了一些相關(guān)人員的關(guān)注。朱學(xué)仁等［4］通過監(jiān)測列車通過杭州市區(qū)某鐵路橋時(shí)，橋墩振動(dòng)引起臨近幾十厘米處的天然氣管道的振動(dòng)響應(yīng)，并用監(jiān)測數(shù)據(jù)結(jié)合相關(guān)規(guī)范對管道安全進(jìn)行理論計(jì)算，得出管道安全運(yùn)行結(jié)論，但這項(xiàng)研究主要針對地上架空管道，其研究成果不適用于埋地管道；吳昭華［5］針對東莞至惠州城際軌道交通項(xiàng)目在運(yùn)營過程中對下穿新奧燃?xì)夤艿揽赡軙斐傻挠绊懀⒘塑壍馈⑺淼澜Y(jié)構(gòu)、土體和管道的三維有限元模型，并采用最不利工況對其進(jìn)行了分析，對燃?xì)夤艿勒＿\(yùn)行安全進(jìn)行了評估，但該項(xiàng)研究針對燃?xì)夤艿溃贿m用于供水管道，且在研究中只考慮了交通振動(dòng)的影響，并未考慮管道內(nèi)部燃?xì)鈱艿赖挠绊懀戳鞴恬詈献饔谩９┧艿琅c天然氣管道有較大區(qū)別，所以以上針對天然氣管道在軌道交通振動(dòng)作用下的振動(dòng)響應(yīng)及研究無法為類似供水管道在軌道交通作用下振動(dòng)響應(yīng)提供參考。

目前尚未見到直接針對地鐵振動(dòng)作用下供水管道振動(dòng)響應(yīng)深入研究的公開報(bào)道，因此本文采用數(shù)值模擬方法，考慮流固耦合作用和地鐵振動(dòng)作用，得出供水管道的振動(dòng)響應(yīng)規(guī)律，以期為今后供水管線設(shè)計(jì)和安全評估提供一些參考。

1 車輛振動(dòng)荷載

潘昌實(shí)［6-7］等把列車的動(dòng)荷載用一個(gè)反映低、中、高頻振動(dòng)特征、附加動(dòng)載和鋼軌面波磨效應(yīng)的激振力函數(shù)來模擬，其經(jīng)驗(yàn)公式為

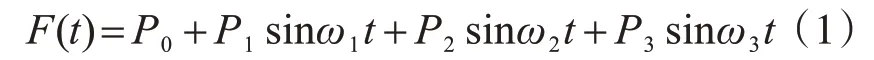
式中：P0為車輪靜載；ω1、ω2、ω3為鋼軌振動(dòng)圓頻率；P1、P2、P3分別對應(yīng)于表1中Ⅰ、Ⅱ、Ⅲ控制條件下某一典型矢高值ai所對應(yīng)鋼軌振動(dòng)荷載幅值。

振動(dòng)荷載幅值為：

式中：M0為車輛簧下質(zhì)量；ωi為相應(yīng)車速下對應(yīng)于表1 中Ⅰ、Ⅱ、Ⅲ控制條件下不平順振動(dòng)波長下的圓頻率。

式中：V為列車的運(yùn)行速度；Li為相應(yīng)車速下對應(yīng)于表1中Ⅰ、Ⅱ、Ⅲ控制條件下不平順振動(dòng)波長。

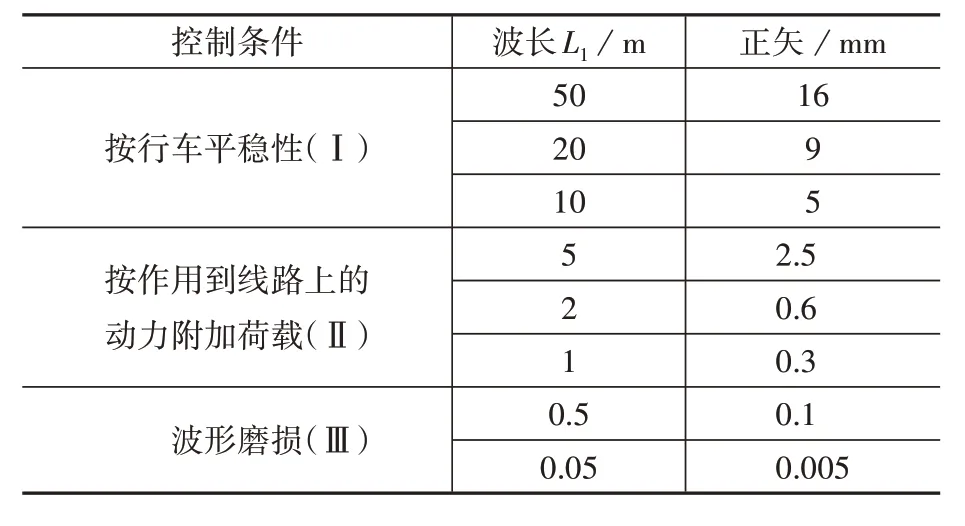
表1 英國軌道幾何不平順幾何參數(shù)Table 1 Geometric parameters of British or bital irregularity

地鐵型號采用文獻(xiàn)［8-9］中的參數(shù)，取單邊靜輪重P0為8×103kg；簧下質(zhì)量為750 kg；不平順波長和相應(yīng)的矢高分別取L1=50和a1=16、L2=5和a2=2.5、L3=0.5和a3=0.1。

根據(jù)以上公式使用MATLAB 進(jìn)行編程，得出列車運(yùn)行速度V=80 km/h 前10 s 的荷載時(shí)程曲線及頻譜圖，如圖1所示。

2 三維有限元模型的建立

為了研究供水管道在地鐵振動(dòng)和流體耦合作用下振動(dòng)響應(yīng)，采用ABAQUS 中的CFD 模塊和Standard/Explicit 模塊分別建立管道-管內(nèi)水流流固耦合模型以及軌道-襯砌-土體-管道三維整體模型。

2.1 模型尺寸及網(wǎng)格劃分

楊永斌［10］通過研究高速列車振動(dòng)時(shí)振源至邊界距離R不同時(shí)計(jì)算結(jié)果的收斂情況，指出當(dāng)R為1.5倍最大剪切波長時(shí)，位移能達(dá)到較好的收斂結(jié)果；呂鐘愛［11］指出當(dāng)有限元網(wǎng)格的尺寸達(dá)到8～10 倍隧道直徑時(shí)分析結(jié)果能有較好的精度；張寶才［12］則認(rèn)為當(dāng)模型深度大于7 倍隧道埋深，寬度大于15 倍隧道直徑時(shí)，模型的自振周期才能趨于穩(wěn)定。結(jié)合以上文獻(xiàn)，為了保證模擬結(jié)果精度，本文根據(jù)最大剪切波長來確定模型尺寸，取180 m×120 m×90 m。研究表明，當(dāng)單元尺寸長度L為λs/6時(shí)，λs為剪切波波長，可以使模擬結(jié)果獲得較好的精度。本文模型中網(wǎng)格劃分如圖2所示。

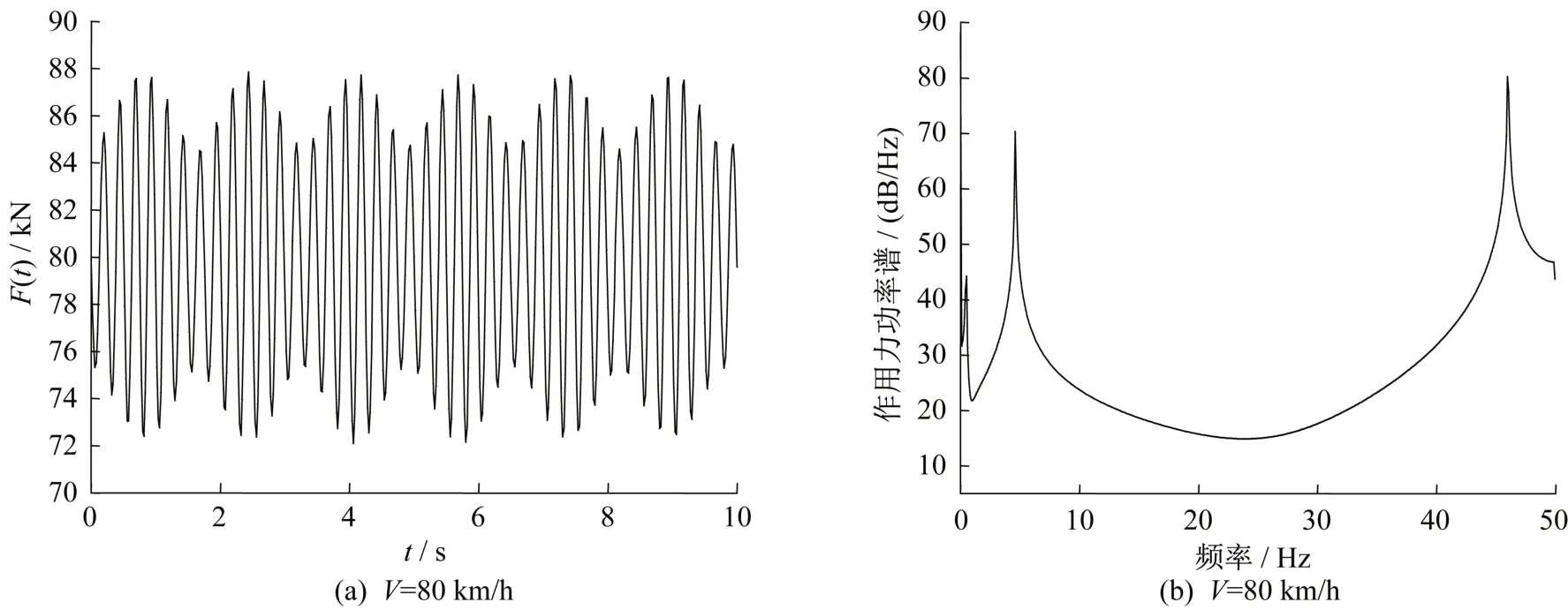
圖1 列車荷載時(shí)程曲線及頻譜圖Fig.1 Train load time history curve and spectrum diagram

圖2 整體有限元模型Fig.2 Global finite element model

圖3 管道有限元模型Fig.3 Finite element pipe model

圖4 流體有限元模型Fig.4 Fluid finite element model

2.2 材料本構(gòu)模型

管道采用高強(qiáng)度X65 管線鋼，材料的本構(gòu)模型采用徐震基于Ramberg-osgood 本構(gòu)方程建立的更加符合實(shí)際的全局二段式應(yīng)力-應(yīng)變本構(gòu)關(guān)系，該本構(gòu)關(guān)系能更好地反映當(dāng)ε＞ε0.2時(shí)X65 管線鋼材料的本構(gòu)關(guān)系［13］，應(yīng)力-應(yīng)變本構(gòu)關(guān)系表達(dá)式如下：

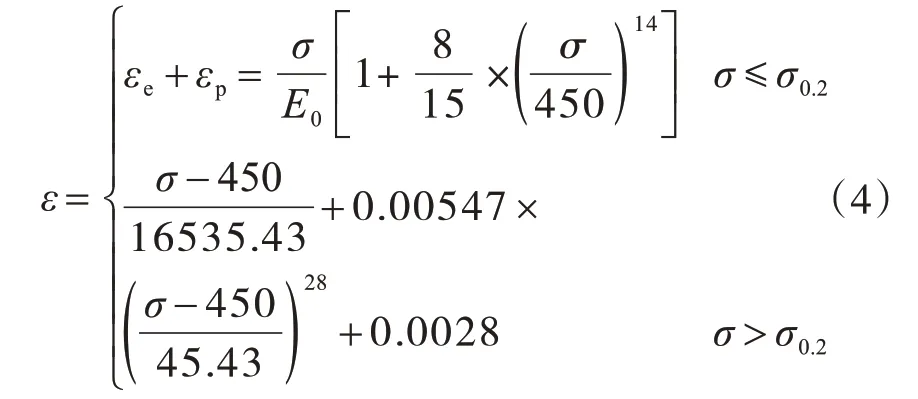
式中：ε為總應(yīng)變；εe為彈性應(yīng)變；εp為塑性應(yīng)變；σ為管材應(yīng)力，單位MPa；E0為材料初始彈性模量，取2.07×105MPa。

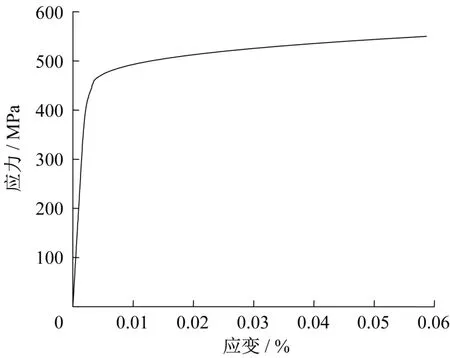
圖5 X65管線鋼的應(yīng)力-應(yīng)變關(guān)系Fig.5 Stress-strain relationship of X65 pipeline steel

軌道交通引起的土體動(dòng)應(yīng)變很小，一般處于彈性變形階段。因此，土體模型采用彈性模型，本構(gòu)關(guān)系可以用胡克定律表示，其式如下：

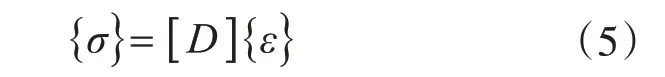
式中：｛σ｝為應(yīng)力增量；｛ε｝為應(yīng)變增量；［D］為彈性矩陣。

管道供水密度取1 000 kg/m3；材料模型選擇EOS 中的 us-up，其中參數(shù) C0 取 1 400；S取 0；Gamm0取0。

2.3 接觸、荷載和邊界條件施加

2.3.1 管土接觸設(shè)置

ABAQUS 數(shù)值模擬中通常采用主控-從屬接觸面算法來模擬復(fù)雜的管土非線性相互作用。該接觸算法中取管道外壁作為接觸對主面，管道四周土體作為接觸對從面且劃分網(wǎng)格時(shí)，從屬表面網(wǎng)格劃分應(yīng)比主控面更精細(xì)，以便計(jì)算收斂［14］。接觸面相互作用分為法向接觸和切向接觸。將法向接觸設(shè)置為硬接觸，既只有當(dāng)接觸面在壓緊狀態(tài)時(shí)才能傳遞法向壓力P，且壓力P大小沒有限制，接觸面存在間隙時(shí)不傳遞法向壓力P，壓力和間隙關(guān)系如圖6所示［15］。

切向設(shè)置為罰函數(shù)，即存在法向接觸壓力P時(shí)，接觸面可以傳遞切向應(yīng)力，摩擦力小于某一極限值τcrit時(shí)，接觸面處于黏結(jié)狀態(tài)，摩擦力大于τcrit時(shí)接觸面發(fā)生相對滑動(dòng)變形，處于滑移狀態(tài)。τcrit的表達(dá)式如下：

式中：μ是摩擦系數(shù)，取 0.3；P為接觸面的法向壓力，單位為Pa。

隧道與周圍土體單元采用綁定約束實(shí)現(xiàn)自由度耦合。

2.3.2 流固耦合作用和地鐵振動(dòng)荷載的施加

管道在受地鐵振動(dòng)作用時(shí)，管內(nèi)流體作用對管道的應(yīng)力場和位移場有很大影響，因此在分析供水管道在地鐵作用下的振動(dòng)響應(yīng)時(shí)，有必要考慮流體和管道的相互作用，進(jìn)行流固耦合分析。流固耦合分析中需要建立固體管道和流體兩個(gè)模型，將管道與流體接觸的耦合表面設(shè)置成Fluid-Structure Co-simulation相互作用，供水管道中存在壓力，將入口和出口壓力設(shè)置為0.6 MPa，同時(shí)考慮到管道中的水沿著管道方向勻速地流動(dòng)，故將入口速度和出口速度設(shè)置為1.4 m/s，然后進(jìn)行耦合求解，得到流固耦合作用下管道的結(jié)果文件，作為接下來分析步的預(yù)定義場，然后輸入上述地鐵振動(dòng)荷載，進(jìn)行管道振動(dòng)響應(yīng)計(jì)算。

2.3.3 邊界條件施加

為了避免散射波在邊界上產(chǎn)生反射造成結(jié)果誤差，本模型土體四周采用劉晶波、杜修力提出的三維黏彈性人工邊界［16］，其表達(dá)式如下：

切向：

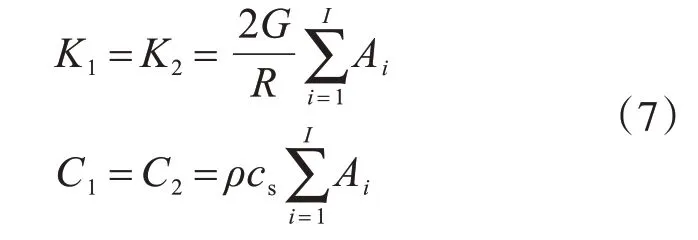
法向：

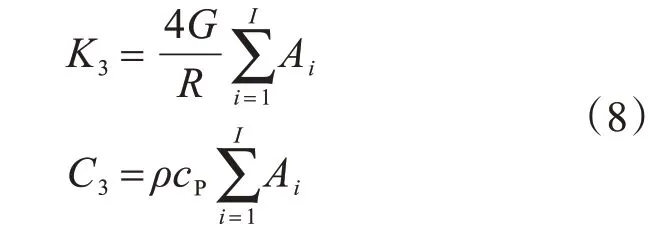
式中：G為介質(zhì)的剪切模量；R為散射源到人工邊界的距離；ρ為介質(zhì)的密度；cs為介質(zhì)的剪切波波速；cp為介質(zhì)的壓縮波波速；∑Ai為人工邊界上節(jié)點(diǎn)所代表的面積。

土體下表面約束x、y、z三個(gè)方向的自由度，上表面不約束自由度為自由表面；襯砌和管道兩端約束x、y、z軸三個(gè)方向的自由度。

3 計(jì)算結(jié)果與分析

依據(jù)上述網(wǎng)格劃分和邊界條件，模型參數(shù)取值如表2 所示。取阻尼比ξ=0.06，根據(jù)模態(tài)分析結(jié)果計(jì)算可得阻尼系數(shù)α=0.12，β=0.022；土層剪切波速取800 m/s。

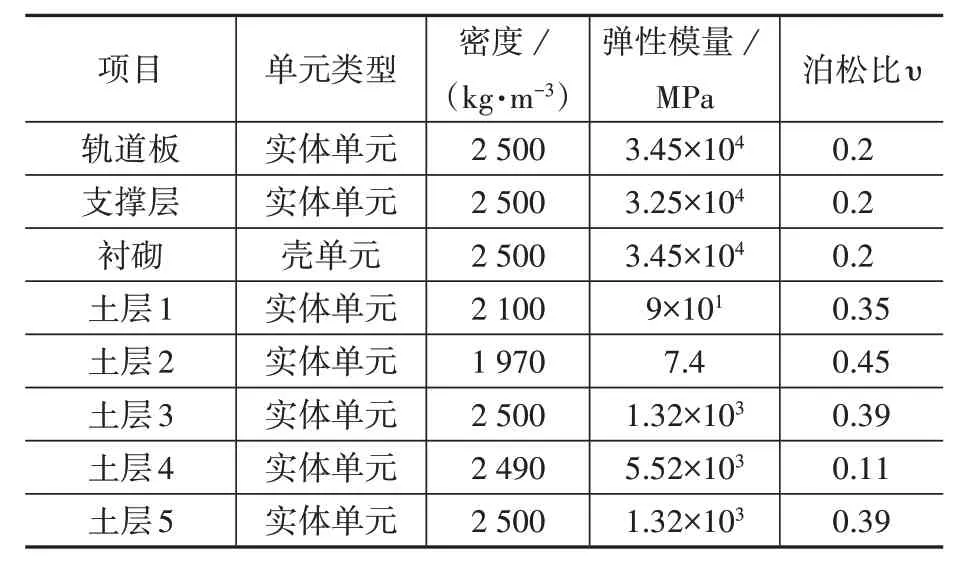
表2 模型參數(shù)Table 2 Model parameters

在上述參數(shù)作用下，分別模擬管線在距隧道中心線不同距離、不同車速、不同埋深、不同管徑等條件下的振動(dòng)響應(yīng)，進(jìn)而得出不同因素對管道振動(dòng)響應(yīng)的影響規(guī)律。現(xiàn)有研究表明，在軌道交通振動(dòng)中，豎向振動(dòng)要遠(yuǎn)大于水平振動(dòng)，故在本文中以豎向Y方向振動(dòng)作為結(jié)果分析參數(shù)。列車速度為80 km/h時(shí)，隧道中心線處管道振動(dòng)速度時(shí)程曲線及頻譜如圖7 所示，加速度時(shí)程曲線及頻譜如圖8所示。

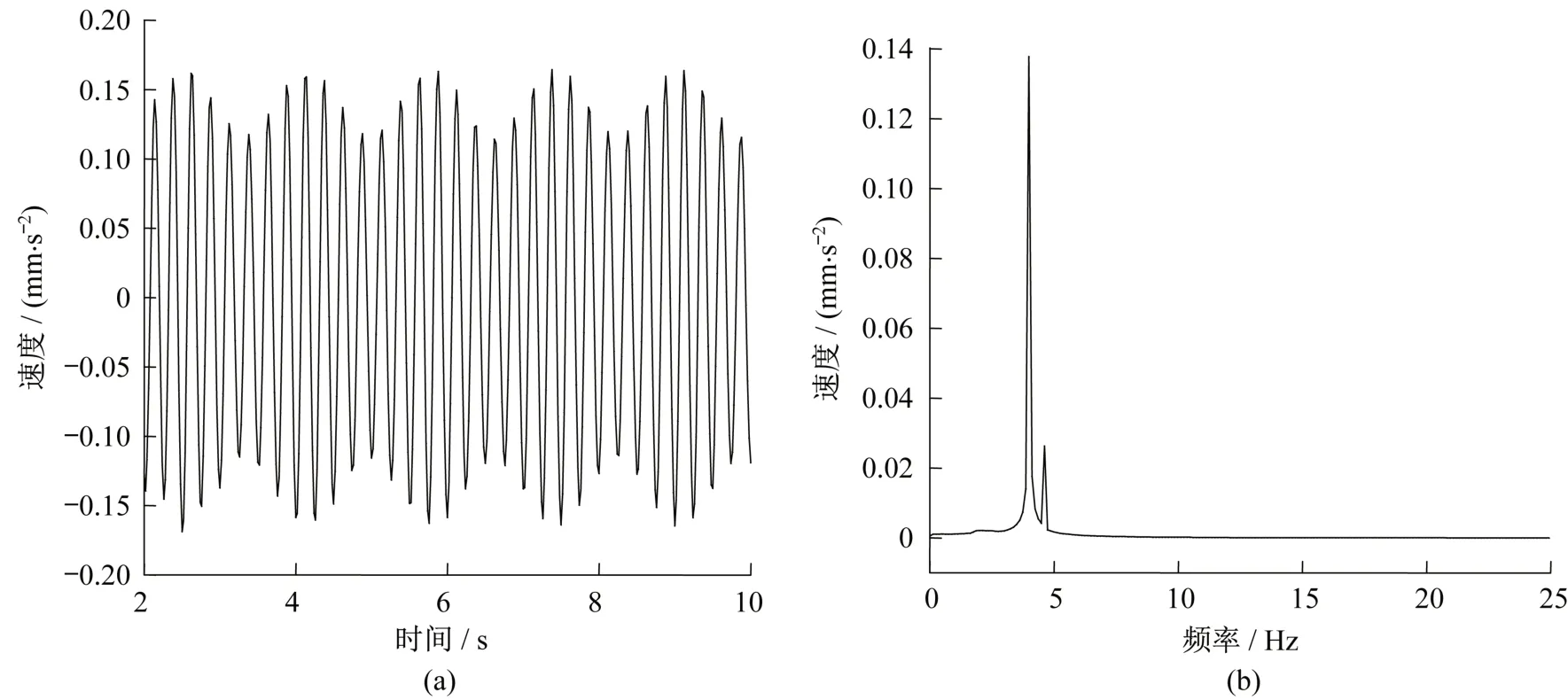
圖7 管道底部振動(dòng)速度時(shí)程曲線及速度頻譜圖Fig.7 Time history curve and frequency spectrum of vibration velocity at the bottom of pipeline

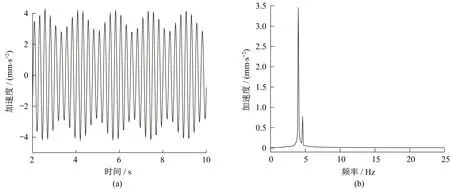
圖8 管道底部振動(dòng)加速度時(shí)程曲線及加速度頻譜圖Fig.8 Time history curve and frequency spectrum of vibration acceleration at the bottom of pipeline

3.1 距隧道中心線不同距離

在車速分別為60 km/h、100 km/h、120 km/h車速下，供水管道底部的振動(dòng)速度峰值、加速度峰值隨距隧道中心線的距離增加變化趨勢如圖9、圖10 所示。從圖中可以看出，管道底部的速度峰值和加速度峰值隨著距離隧道中心線距離的增大都呈現(xiàn)出衰減趨勢，且在0 m 到60 m 范圍內(nèi)衰減幅度較大，60 m 之后衰減幅度較小，幾乎沒有變化。以車速100 km/h 為例，距隧道中心線0 m 到60 m的范圍內(nèi)，速度峰值從0.24 mm/s降低到0.04 mm/s，下降了約83.3%，加速度峰值從8.2 mm/s2降低到1.4 mm/s2，下降了約83%。由此可見，在對受地鐵振動(dòng)影響的供水管線監(jiān)測中，要對隧道中心線60 m范圍內(nèi)的管線進(jìn)行重點(diǎn)監(jiān)測。

3.2 不同車速

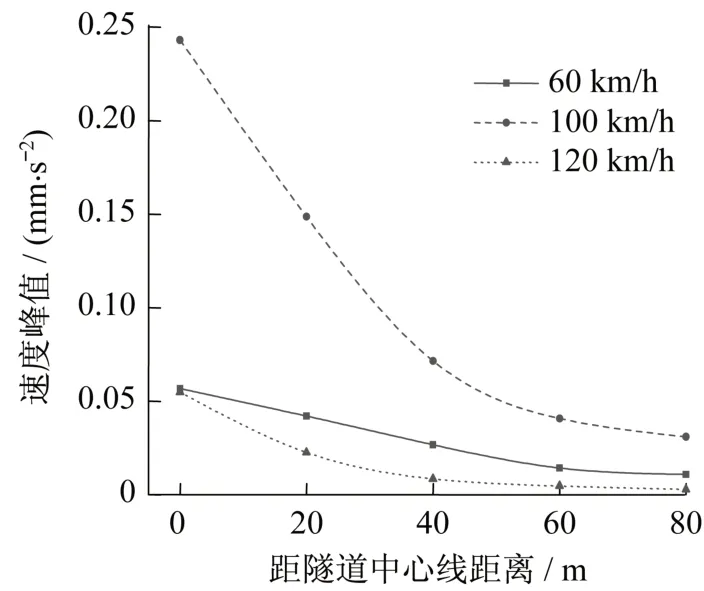
圖9 管道底部速度峰值隨距離變化圖Fig.9 Diagram of velocity peak at the bottom of the pipe changing with distance

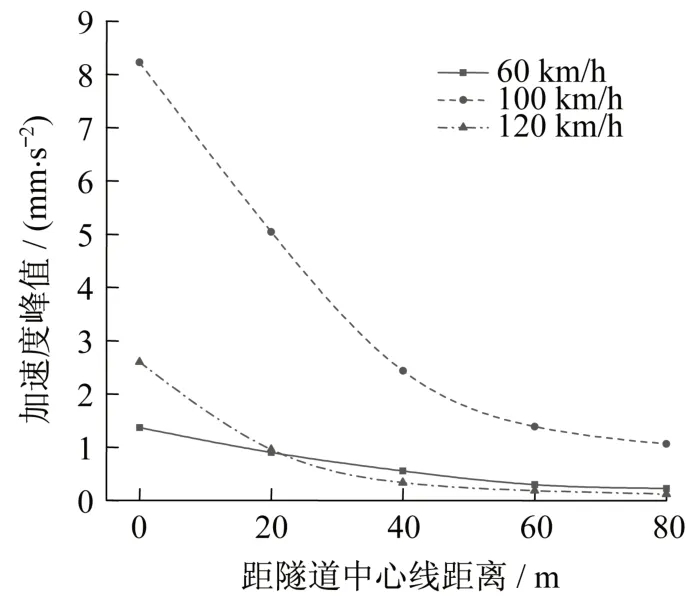
圖10 管道底部加速度峰值隨距離變化圖Fig.10 Diagram of peak acceleration at the bottom of the pipe changing with distance

在車速分別為 40 km/h、60 km/h、80 km/h、100 km/h、120 km/h 等五種固定車速條件下，分別提取距隧道中心線0 m、20 m、40 m、60 m、80 m 處管道底部的最大振動(dòng)速度峰值（圖11）和加速度峰值（圖12）。從圖中可以看出，管道距離隧道中心線相同位置處在不同車速下速度峰值和加速度峰值的變化趨勢基本一致。管道振動(dòng)的速度峰值和加速度峰值在車速從40 km/h 增加到100 km/h時(shí)增加幅度較大，以距隧道中心線0 m 處的振動(dòng)響應(yīng)規(guī)律為例，速度峰值從0.031 mm/s 增加到0.24 mm/s，加速度峰值從0.43 mm/s2增加到8.23 mm/s2；當(dāng)速度從 100 km/h 增加到 120 km/h時(shí)，速度峰值和加速度峰值都出現(xiàn)了比較快的衰減，可見在速度增加的過程中存在一個(gè)卓越車速使管道的振動(dòng)響應(yīng)達(dá)到最大值，對管道運(yùn)行安全極為不利。

3.3 不同埋深

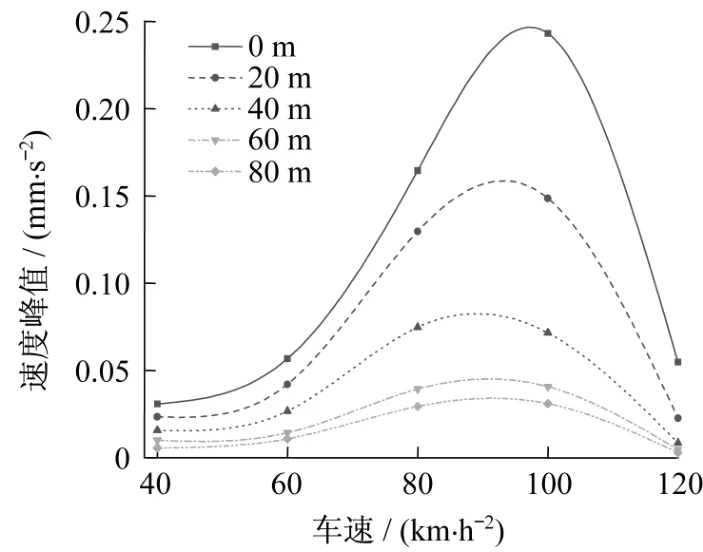
圖11 不同車速下速度峰值Fig.11 Peak speeds at different speeds

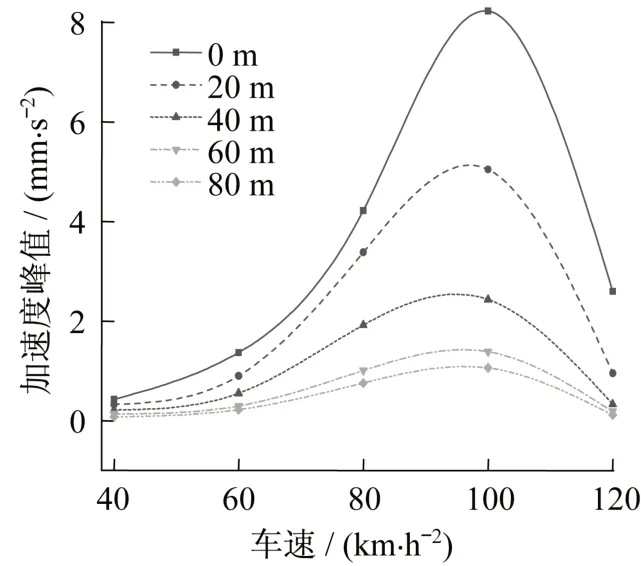
圖12 不同車速下的加速度峰值Fig.12 Peak acceleration at different speeds

在車速為100 km/h 的車速下，分別模擬管道埋深為1 m、1.5 m、2 m、2.5 m、3 m 的最大速度峰值和加速度峰值如圖13、圖14所示。從圖中可以看出，管道在不同埋深情況下速度峰值和加速度峰值曲線走勢基本相似。隨著埋深的減小距隧道距離中心線相同距離處速度峰值呈增加趨勢，從0.24 mm/s 增加到了0.29 mm/s，增加了約20.8%，但在2 m 和2.5 m 處會出現(xiàn)反彈，可能是因?yàn)榇颂幪幱趦赏翆咏唤缣帲蠈訋r體的密度和彈性模量都比下層巖體較大，波透過此邊界時(shí)會發(fā)生折射和反射所致。隨著埋深的減小加速度峰值呈增加趨勢，加速度從7.25 mm/s2增加到8.23 mm/s2，增加了約14%。可見，埋深越小管道振動(dòng)響應(yīng)越大，對管道安全運(yùn)行越不利。

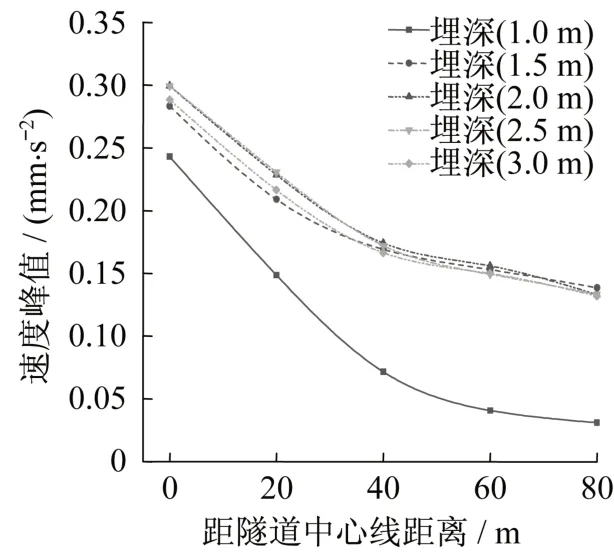
圖13 不同埋深下速度峰值Fig.13 Peak velocity under different burial depths

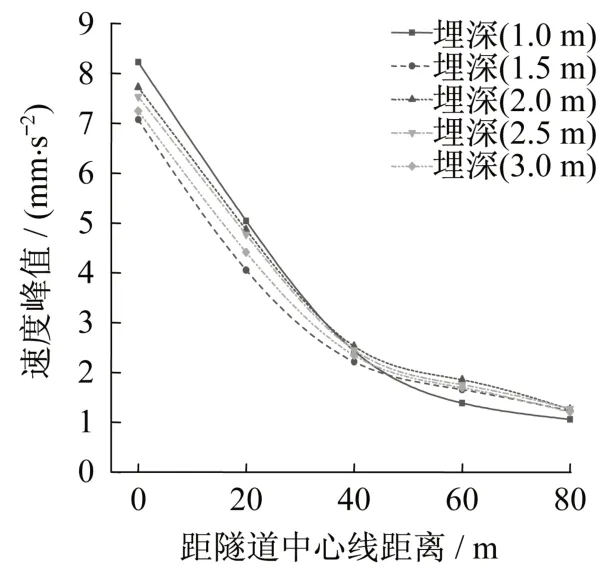
圖14 不同埋深下加速度峰值Fig.14 Peak acceleration at different burial depths

3.4 不同管徑

在車速100 km/h、埋深1 m 的工況下，分別模擬管道直徑為1 m、1.2 m、1.4 m、1.6 m、1.8 m 最大速度峰值和加速度峰值如圖15、圖16所示。從圖中可以看出，隨著管徑的增大，管道的速度峰值和加速度峰值均呈現(xiàn)增加趨勢。管道直徑從1 m 增加到1.8 m 的過程中，管道速度峰值從0.21 mm/s增加到0.32 mm/s，增加了52.4%；管道加速度峰值從7.6 mm/s2增加到約18.6 mm/s2，增幅較大，大約增加了144.7%。可見，相同條件下，管道直徑越大，振動(dòng)響應(yīng)越大，在設(shè)計(jì)受地鐵振動(dòng)影響的供水管道時(shí)，滿足設(shè)計(jì)要求的情況下，應(yīng)盡量采取較小直徑。

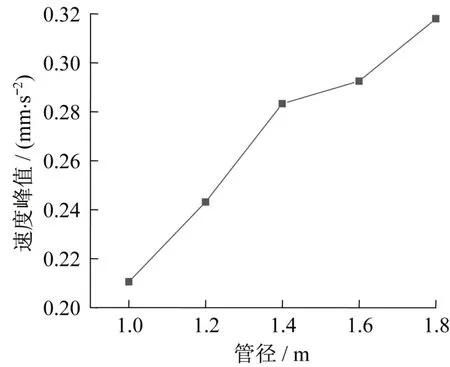
圖15 不同管徑下速度峰值Fig.15 Peak velocity at different pipe diameters

4 結(jié) 論

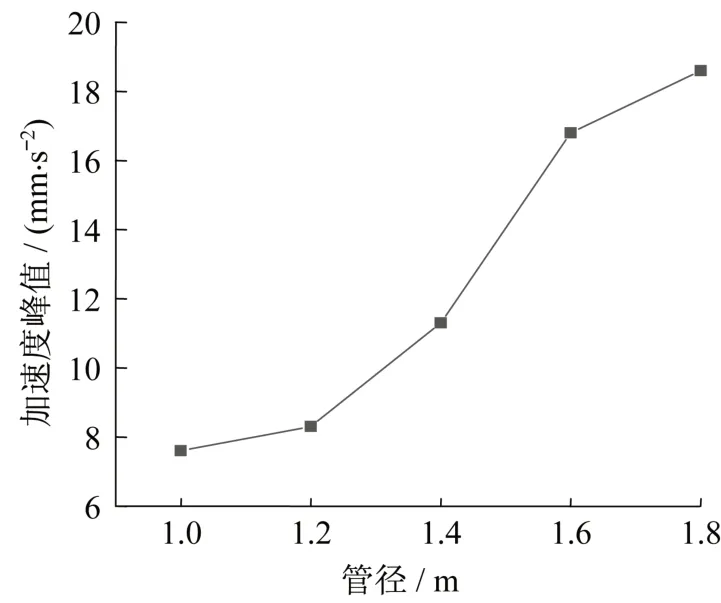
圖16 不同管徑下加速度峰值Fig.16 Peak acceleration at different diameters

地鐵運(yùn)行時(shí)產(chǎn)生振動(dòng)會通過軌道-襯砌-土體傳至供水管道，從而引起管道振動(dòng)響應(yīng)，進(jìn)而對供水管道造成影響破壞。使用ABAQUS 軟件，分別建立流體-管內(nèi)水流流固耦合模型和軌道-襯砌-土體-管道整體模型，分析供水管道在管內(nèi)水流和地鐵振動(dòng)耦合作用下的振動(dòng)響應(yīng)，得出以下結(jié)論：從模擬結(jié)果上來看，在管內(nèi)水流和地鐵振動(dòng)耦合作用下，速度峰值和加速度峰值都隨著距隧道中心線的距離增加而減小；隨著速度的增加而增加，且當(dāng)車速達(dá)到一定速度后，隨著速度的增加減小，表明存在一個(gè)卓越車速，在這個(gè)卓越車速下，管道的振動(dòng)響應(yīng)會出現(xiàn)極大值；隨著埋深的增加而減小；隨著管徑的增大而增大。在實(shí)際工程中，應(yīng)該根據(jù)實(shí)際工況來確定管線設(shè)計(jì)、埋深、管徑等參數(shù)。