設置非線性黏滯阻尼耗能框架結構等效阻尼及地震作用分析

張 敏 陳豆豆

（1.江西科技師范大學建筑工程學院，南昌330013；2.廣西科技大學土木建筑工程學院，柳州545006）

0 引 言

耗能減震是一種結構被動控制技術，該技術是在結構中設置阻尼器，并在地震作用中，該阻尼器產生彈塑性變形，耗散地震輸入結構的能量，進而保護結構免遭地震破壞［1-3］。非線性黏滯阻尼器是一種速度相關型減震裝置，該阻尼器通過兩端產生相對速度，從而對結構施加阻尼力F=C|V|α，其中，C為阻尼系數，|V|為阻尼器兩端相對速度絕對值，α為阻尼指數。目前已在建筑、橋梁中被廣泛應用，同時，與其相適應的分析理論也不斷發展。由于該結構構造簡單，且工作時不改變結構剛度，因此在框架結構中設置非線性黏滯阻尼器，降低結構地震反應，是減震控制的一種有效形式，但設置非線性粘滯阻尼器后結構各階振動的阻尼比如何確定？結構地震作用如何分析？不少學者對該問題做了大量研究。

1998 年，歐進萍基于國內外減震裝置性能試驗，結合抗震規范，提出了阻尼器等效阻尼和等效剛度的計算方法，以及適用于反應譜法的附加振型阻尼比方法［4］，將減震結構設計轉化為抗震結構設計；2007 年，程光煜將等效線性法應用于能力譜計算，對比分析了8 種等效線性化方法的地震輸入能量譜的精度［5］，證明現有應用于能力譜計算的等效線性法，等效周期偏小，誤差較大；2009 年，陸偉東針對中、美、日3 國規范中等效阻尼比的計算進行對比分析，根據日本規范設計思路，提出更為精確的計算公式，并將該公式計算結果，用于三層混凝土框架，進行時程分析比較［6］，證明該方法有良好的精度；2010 年，梁仁杰針對單自由度和多自由度體系，分別采用考慮等效阻尼比的傳統能力譜法和采用彈塑性反應譜的改進方法進行分析比較，并和非線性時程分析對比［7］，結果表明：采用傳統方法低估了結構響應，有較大誤差，而采用彈塑性需求曲線的改進方法和真實反應吻合較好。2011 年，李創第采用隨機平均法，分別對單自由度、多自由度帶支撐Maxwell 阻尼器減震結構的等效阻尼比進行了系統研究，建立了耗能結構各振型等效阻尼比的計算式［8-9］，與模態應變能法的計算精度進行對比分析，結果表明該方法優于應變能法；2014 年，宋力勛提出了純阻尼器和考慮支撐剛度阻尼器的等效阻尼比計算公式［10］，結果證明：明確阻尼器位置和參數，可通過計算公式計算等效阻尼比。同年，王婷用ATC-40 中的能力譜法對一棟三層混凝土框架結構進行安全性驗證，證明該方法對等效阻尼比估計過高［11］，導致對地震反應估計偏低，在此基礎上，擬合出改進等效阻尼比模型，該模型能較好地估計地震反應。2016 年，何文福對黏滯阻尼器結構進行附加等效阻尼比的研究，并提出動力響應減震系數法計算附加等效阻尼比，對比幾種附加阻尼比計算結果［12］，證明 Constantinou 提出的近似公式計算結果與時程分析最為接近。2016 年，張敏采用狀態方程直接積分法，研究了一棟10 層線性黏滯阻尼耗能框架結構的地震響應，提出了阻尼系數優化公式，并根據阻尼比不同，提出了適用于不同阻尼比的地震作用實用計公式［13］，證明阻尼器在結構各樓層均勻布置時，框架結構的地震響應較傳統抗震結構減少很多。2018 年，Li 提出了一種確定SDOF 結構的一階和二階等效黏性阻尼和剛度、峰值響應及其阻尼力的新方法，基于一般線性黏彈性阻尼結構的動力特性，提出了改進的多時間尺度法，采用所有自由振動特性相同的等效準則，得到結構的一階和二階等效黏性阻尼和剛度［14］，證明該方法比模態應變能法的精度更高，且明顯優于模態應變能法。2018 年，周瑞指出中美日三種設計標準均直接或間接以地面運動峰值加速度作為地震反應譜的基準數據，以中國標準的αmax為比較基準，比較了鋼框架和鋼筋混凝土框架在三種標準下的地震響應最大值的關系［15］，給出確定地面運動峰值加速度的方法，可以正確地計算出結構地震響應。2018 年，耿耀明針對設置黏滯流體阻尼器的裝配整體式鋼筋混凝土框架結構，采用反應譜法和彈性時程分析法分析結構地震響應［16］，發現多遇地震下黏滯阻尼器耗能明顯，能夠保護主體結構，罕遇地震耗能較多遇地震減少，但仍可消耗部分能量，從而保護主體結構。同年，賈傳果對非線性阻尼力進行線性化處理，形成黏滯阻尼器減震結構運動方程，并給出求解局部非線性結構動力問題的數值積分方法［17］，通過 Matlab 對帶黏滯阻尼器的七層平面框架進行地震響應分析，證實該方法的可靠性。

非線性黏滯阻尼器具有較強的非線性，其等效阻尼比分析較復雜。本文基于阻尼器能量耗散概念，根據各階振動的不同振動形式及其正則坐標幅值不變的原則，分析各階振動的等效阻尼比，并由此分析結構的地震作用。

1 結構地震作用分析

分析結構各樓層地震作用，是將結構地震作用的動力分析問題轉化為相當于結構靜力荷載作用的靜力分析問題。各樓層地震作用為

令{x}=[φ]{q}，經變換可得：

式中，ωnj為框架結構第j振型的振動頻率。

第j振型結構地震作用向量為

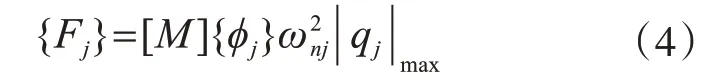
設置非線性黏滯阻尼器框架結構，第j振型第i樓層的結構地震作用為

可見結構地震作用與結構正則坐標qj的幅值有關。

2 耗能框架結構等效阻尼比分析

2.1 框架結構各階振動阻尼器耗能

為了將減震結構地震作用計算轉化為抗震結構采用反應譜法計算，本文提出將非線性阻尼轉化為結構等效阻尼。

本文采用的非線性黏滯阻尼器的阻尼力F=C|V|α，其中，C為阻尼系數，α為阻尼指數，V為阻尼器兩端相對速度。

圖1 所示框架結構設置非線性黏滯阻尼器的振動方程為

式中：[M]、[C]、[K]分別為結構的質量矩陣、阻尼矩陣、剛度矩陣；{Fd}為非線性黏滯阻尼器對框架結構作用力向量。

若僅考慮第j陣型，則{x}={φj}qj，化簡可得

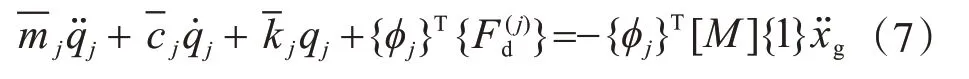
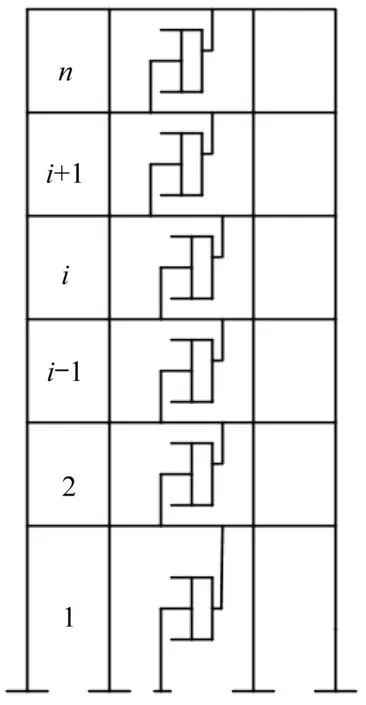
圖1 結構模型Fig.1 Structure model

對式（7）兩邊各項分別積分，則得

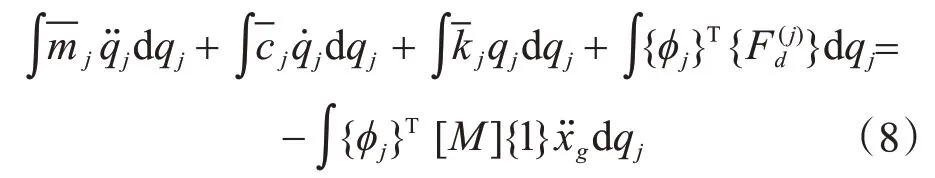
式中，等式左邊四項分別代表結構第j振型振動時的動能、結構自身阻尼耗能、結構彈性勢能和非線性黏滯阻尼耗能；等式右邊代表地震輸入結構的能量。

第j振型一個振動周期的阻尼耗能為

可得

其中，[hj]=diag(hj1，hj2，…，hjn)。

將式（13）代入式（9）中，得

化簡，得

式中，qjm為第j振型正則坐標qj的幅值。

2.2 等效阻尼比分析

結構設置非線性粘滯阻尼器后等效為結構線性黏滯阻尼，即

結構阻尼等效原則如下：

（1）阻尼等效前后結構阻尼耗能總量不變；

（2）阻尼等效前后結構按第j振型正則坐標幅值不變，即qjm不變。

阻尼等效后的振動方程：

僅考慮第j陣型{φj}，式（20）可變換得：

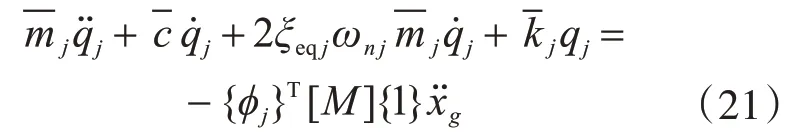
式中，ξeqj為第j振型等效阻尼比。

一個振動周期等效阻尼耗能：

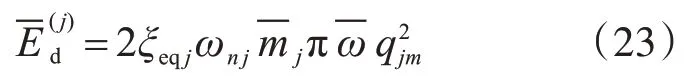
求得，

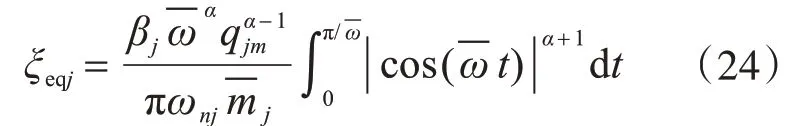
將方程（21）右邊地震波幅值視為靜載，產生的靜力反應qstm為

式中：Amax為地震波x¨g(t)的幅值；γj為第j振型參與系數。

令第j振型振動的動力放大系數則

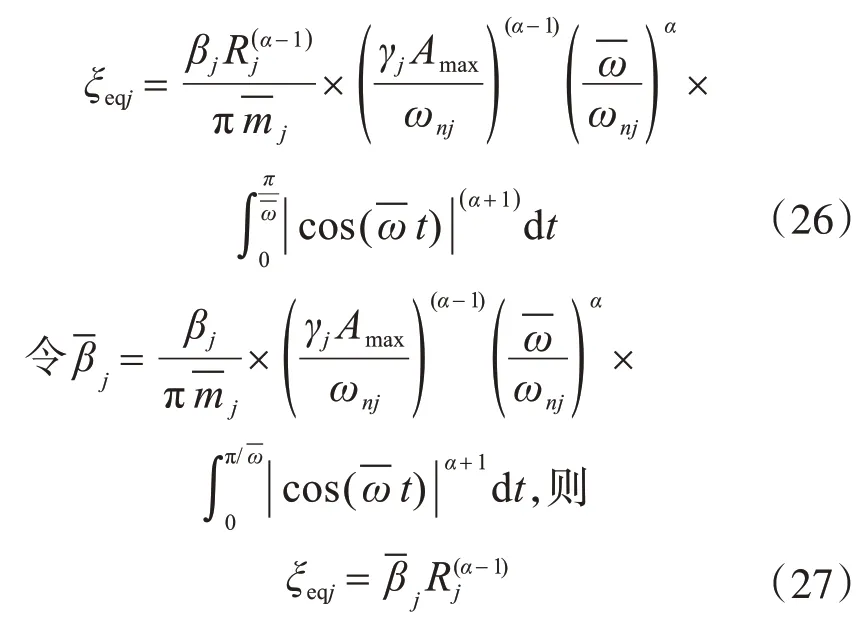
由結構動力學，可得

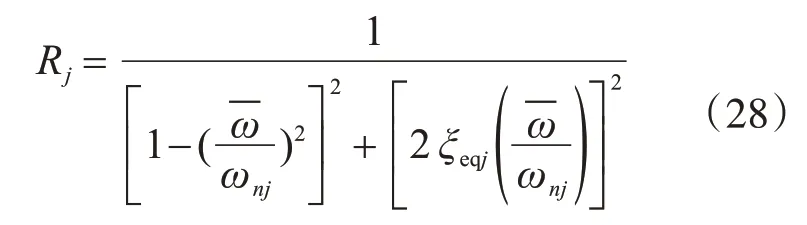
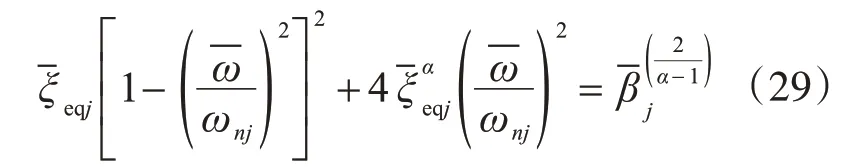
2.3 結構高階振動等效阻尼比分析

根據《建筑抗震設計規范》（GB 50011—2010）振型分解反應譜法，結構第j振型第i樓層地震作用為

阻尼等效后，由式（5）和式（31），可得

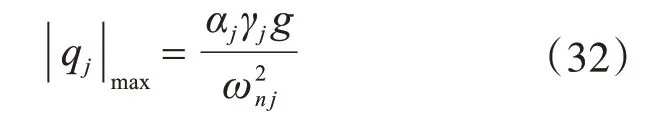
對于第1振型，則

由式（32）、式（33）變換為

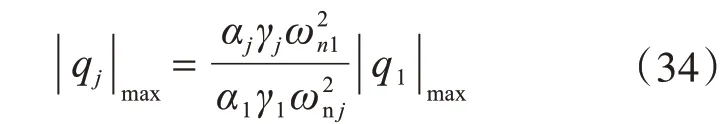
若僅考慮第j陣型時，將式（21）進行傅里葉變換并化簡，得

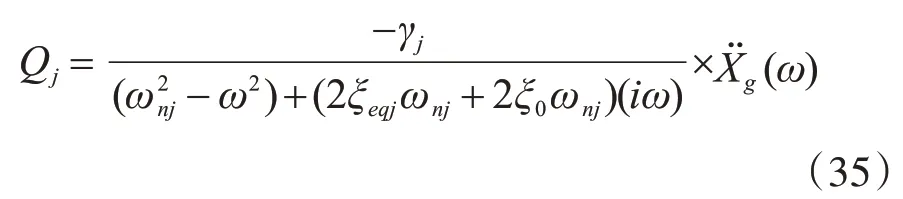
式中，ξ0為設置非線性黏滯阻尼器前，框架結構自身阻尼比，一般取ξ0=5%。即

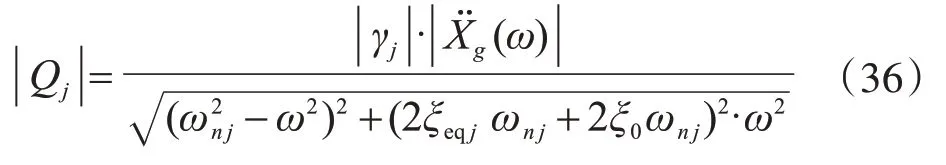
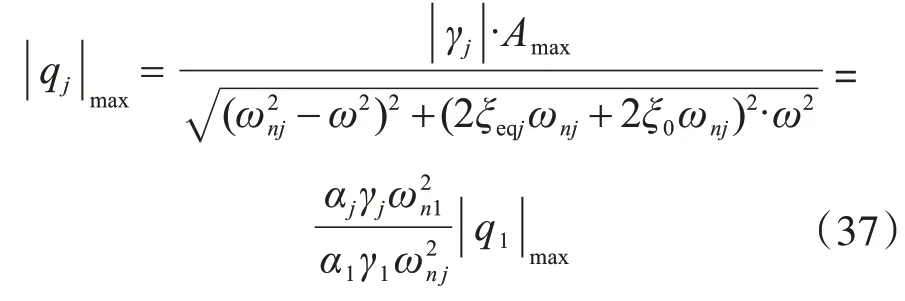
當j=1時，則

式中，ω近似取為場地特征頻率

式（37）可變換為

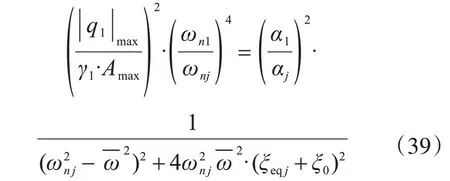
根據《建筑抗震設計規范》（GB 50011—2010），可得為

將式（40）代入式（39），可得

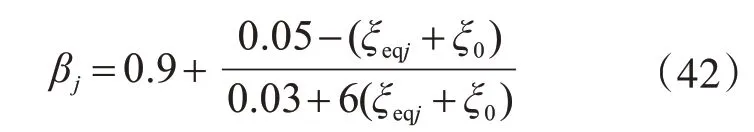
求解式（44），可得ξeqj，將ξeqj代入式（37）可求出|qj|max。

3 工程算例

一棟10 層鋼筋混凝土框架結構，平面布置見圖2。底層層高4.5 m，二層及以上樓層高度為3.3 m，總層高為34.2 m；該結構設防類別丙類，抗震設防烈度為8度，基本地震加速度0.3g，設計地震分組為第2組；結構自身阻尼比ξ0=0.05；混凝土強度等級C30；樓屋面折算恒載標準值10 kN/m2（包括墻體自重），樓屋面活載標準值2 kN/m2；梁截面尺寸為300 mm×650 mm，柱截面尺寸為600 mm×750 mm。每榀橫向框架各樓層均勻設置阻尼器，見圖1，阻尼參數設置如下：I類場地，C=1 000 kN·s·m-1，α=0.5；Ⅱ、Ⅲ類場地，C=1 800 kN·s·m-1，α=0.5。該結構分別作用OROVILLE地震波（適用I類場地）、El-Centro 地震波（適用Ⅱ類場地）、HOLLYWOOD STORAGE地震波（適用Ⅲ類場地）。各地震最大加速度幅值均調整為110 cm/s2。

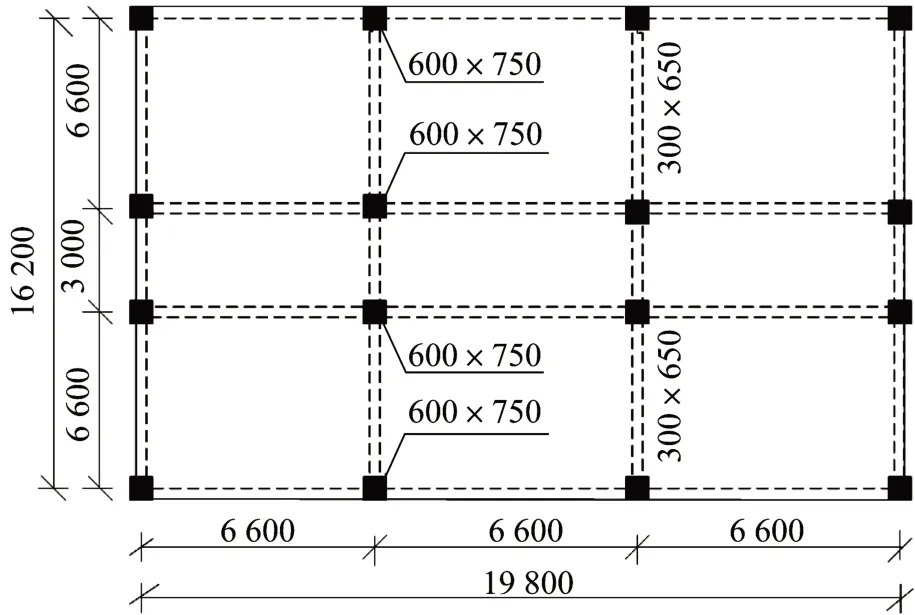
圖2 結構框架平面圖（單位：mm）Fig.2 Plane layout of frame structure（Unit：mm）

3.1 一階振動等效阻尼比

根據式（31）計算，各類場地一階振動的等效阻尼比見表1。

表1 一階振動等效阻尼比Table 1 Equivalent Damping Ratio of First Order Vibration

3.2 一階振動q1時程曲線

阻尼等效前后各類場地一階振動的正則坐標q1時程曲線見圖3。可見，阻尼等效前后q1時程曲線基本吻合。

圖3一階正則坐標時程曲線Fig.3 Regular coordinate time curve of structures

3.3 一階振動

3.4 地震作用

阻尼等效后，結構地震作用按式（5）計算，并與抗震結構相應值對比，見圖4。

表2 一階振動Table 2 of first order vibration

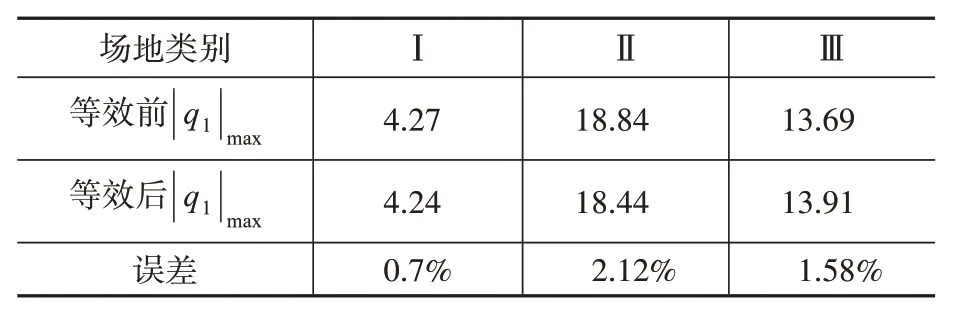
表2 一階振動Table 2 of first order vibration

ⅠⅡⅢ場地類別等效前|q1|max等效后|q1|max誤差4.27 4.24 0.7%18.84 18.44 2.12%13.69 13.91 1.58%

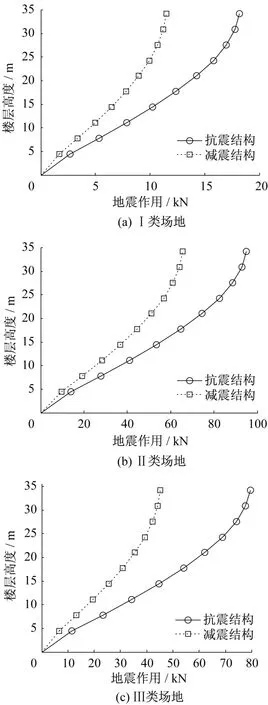
圖4 地震作用Fig.4 Seismic action

4 結 論

本文針對設置非線性黏滯阻尼器框架結構，利用阻尼器耗能及正則坐標幅值不變原則，推導出適用于設置非線性黏滯阻尼器框架結構的各階振型等效阻尼比的計算公式，從而可將減震結構地震作用計算問題轉化為抗震結構的反應譜法計算。最后對一棟10 層框架結構分別作用Ⅰ、Ⅱ、Ⅲ等三類場地地震波，分析阻尼等效前后一階正則坐標時程曲線，表明采用本文給出的等效阻尼比進行分析，兩種時程曲線吻合性較好。

綜合前文分析，結論總結如下：

（1）設置非線性黏滯阻尼器框架結構各樓層地震作用可采用式（45）計算。

（2）設置非線性黏滯阻尼器框架結構第一階振動的等效阻尼比ξeq1為

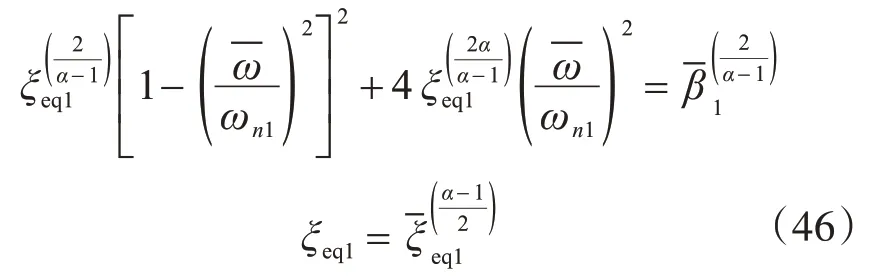
（3）設置非線性黏滯阻尼器框架結構高階振動的等效阻尼比ξeqj，可由下列方程求解：