基于自相關峰值變化率的古木結構損傷識別

侯艷芳 胡衛兵 楊 佳

（1.西安建筑科技大學土木工程學院，西安710055；2.陜西工業職業技術學院土木工程學院，咸陽712000）

0 引 言

中國古建筑是人類文化遺產中獨具特點又彌足珍貴的一支，蘊含了浩瀚無涯的精神文化，它既能客觀地反映歷史的發展脈絡及其面貌，又能將許多文字無法記錄的史料保存至今。中國古建筑內涵深厚而形神皆備，它具有許多特質，在技術方面善于運用木結構，將木材技術發揮到極致，為世界其他文明所罕見［1］。在千百年的使用過程中，由風雨侵蝕、自然災害、材料老化和長期荷載作用等因素共同作用，中國古木建筑已存在不同程度的損傷和破壞。近現代交通（地鐵等）所產生的高頻微幅振動，在原有損傷的基礎上不斷累積損傷并使抗力衰減，從而在自然災害發生甚至是在正常環境作用下結構發生損壞的可能性大幅提高。一座古建筑就是一本立體的且無法復制的史書，一旦消失其損失無法彌補。若能利用有效的方法和手段對古木建筑進行損傷識別和評定，進而及時控制和修復損傷，避免結構的損壞，對古建筑的修繕和保護具有重要意義。

傳統的檢測方法通常采用人工激振，但是該方法需要較大的激振能量，容易引起古建筑木結構的損傷，反而對研究起到反作用。因此，利用環境激勵（車輛、風、機械振動等）下的結構振動響應數據進行損傷檢測成為結構健康監測中的熱點［2］。

于哲峰［3-5］等提出了互相關函數幅值向量的概念，以某測點k為參考點，將其他各測點與參考點之間的互相關函數的最大值rkl組成一個幅值向量，進行了隨機激勵下基于互相關函數幅值向量的結構損傷檢測的實驗研究及損傷定位方法研究。楊智春等［6］提出了基于互相關函數幅值向量和連續小波變換聯合檢測損傷的方法。黨曉娟等［7-8］提出了基于互相關函數幅值向量與統計學原理相結合的損傷統計檢測方法，通過對一個復合材料層合懸臂板進行分層損傷檢測的數值模擬，驗證了該方法的有效性；并將互相關函數幅值向量與離散小波分解結合起來，提出了一種損傷檢測新方法。

雷家艷［9］以相鄰兩測點的動力響應時程為基礎，定義了新的互相關函數幅值向量和損傷因子，并通過試驗數據分析驗證了該方法的可行性。由于沒有了參考點的牽制，對損傷的局部反映更直觀。

本文根據相關函數的原理，計算各振動測點的自相關函數，并將所有的峰值組成自相關函數幅值向量；計算兩個完好結構的自相關函數幅值向量之間的互相關系數，以此作為結構損傷識別的基準值。計算結構損傷前后各測點自相關函數峰值的變化率，確定結構的損傷位置。通過算例分析，驗證了該方法的可行性。

1 相關函數的基本理論[10-12]

1.1 相關與相關函數

相關是信號分析中一個非常重要的概念。相關函數有互相關函數和自相關函數，分別表示兩個時間序列之間或同一個時間序列在任意兩個不同時刻取值之間的相關程度，即：互相關函數描述的是兩個信號x（t）和y（t）在任意兩個不同時刻t1、t2的取值之間的相關程度；自相關函數表示信號x（t）在某一時刻的數據與另一時刻的數據之間的依賴關系。

對于連續型隨機過程，信號x（t）與y（t）的互相關函數記為

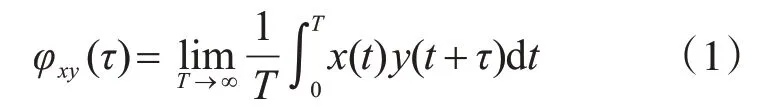
式中，T為所取信號的時間過程，τ表示兩個信號取值的時間差，稱為滯后。

若隨機變量是離散型隨機序列，則兩個信號之間的互相關函數表示為

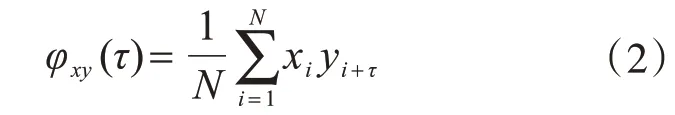
式中，N為隨機序列的離散值數；τ為時間間隔。

如果y（t）=x（t），表示信號x（t）與自己的時延信號x（t+τ）的相似程度，也即是自相關函數。

連續型隨機變量的自相關函數為

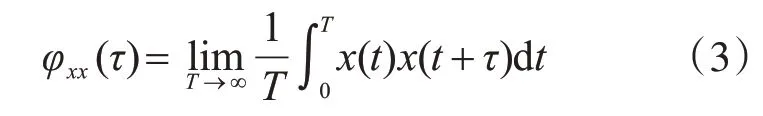
離散型隨機序列的自相關函數為

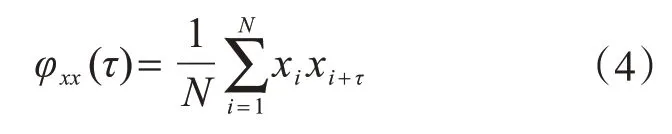
φ（τ）的大小可以定量的衡量兩組信號之間的相似程度。φ（τ）的數值不僅與兩個信號自身的特點有關，還與兩組信號之間的時間間隔τ有關。φ（τ）的最大值所對應的τ=τi值表示，當兩個信號的時延為τi時，它們之間最相似。

1.2 自相關函數幅值向量及互相關系數

根據相關函數的概念，隨機過程兩個狀態之間的相關程度，總不會大于在同一個點上的狀態與其自身的相關程度，所以自身與自身強相關。因此，求隨機振動結構各測點的自相關函數能更明確反映出結構損傷前后各測點峰值的變化程度。

自相關函數在τ=0 時取得最大值。這是因為此時x（t+τ）就是與x（t）自身求相關，相關程度最大。所以，φxx（τ）的最大值為φxx（0）。

對于隨機振動的結構，若同時測得n個測點的動力響應（加速度、速度、位移等），則各測點動力響應的自相關函數為

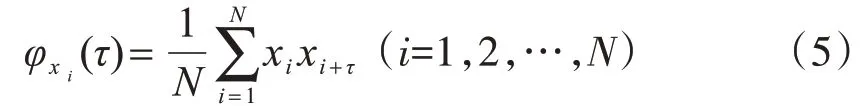
當τ=0 時，記各測點xi的自相關函數φxi（τ）的最大值為：φxi（0）=δii，由所有的最大值組成的自相關函數幅值向量為

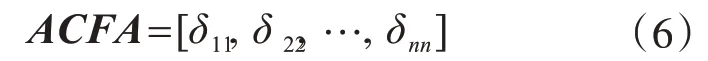
在后面的計算中，為表達方便，自相關函數幅值向量簡記為A。

表示兩組信號相關程度的一個重要特征數值是互相關系數：

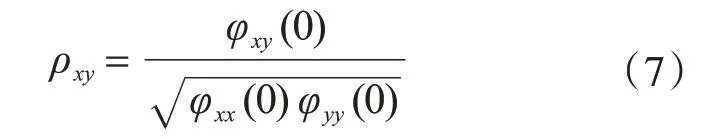
互相關系數ρxy表達的是兩組信號或向量之間的相關程度，其取值范圍為［0，1］。當x（t）=y（t），即信號與自身相關時，ρxy=1；當x（t）和y（t）不相關時，ρxy=0。

互相關系數ρ越大，相關程度就越高；反之，ρ值越小，也就說明兩組向量之間的相關性越小。因此，可以根據損傷結構與完好結構的ACFA之間互相關系數的大小判別結構是否發生了損傷，即可以將互相關系數作為結構損傷識別的損傷因子。

1.3 自相關函數幅值向量的固定形態

設x（t）是遍歷過程的一個樣本函數，它是定義在（-∞＜t＜∞）區間內的一個非周期函數，一般不滿足絕對可積條件，進行傅里葉變換時需要引入截尾函數，即x（t）是指在有限時間區間上的截尾函數。x（t）和x（t+τ）的傅里葉變換為

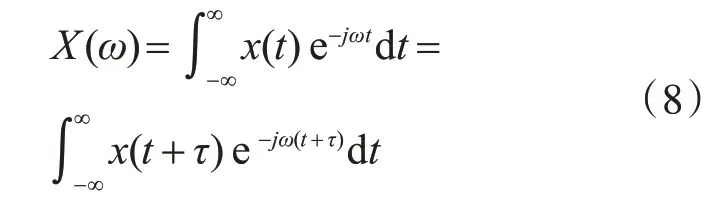
它們的傅里葉逆變換為

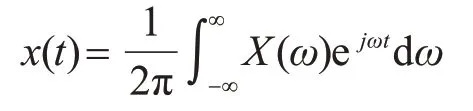
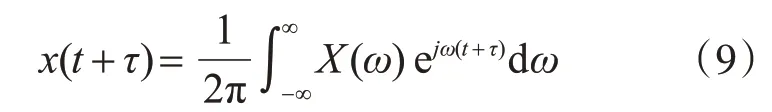
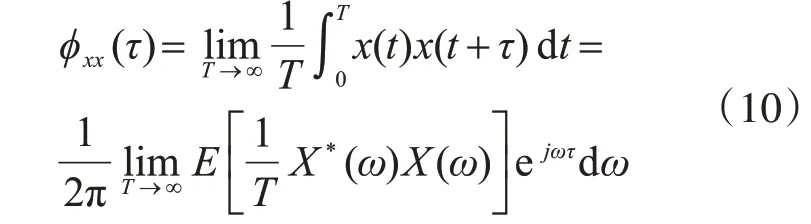
其中，X*(ω)是X(ω)的共軛。

設結構所受激勵荷載f(t)的傅里葉變換為

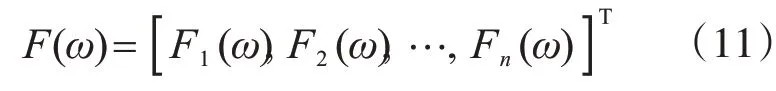
結構頻率響應函數的第j行為：

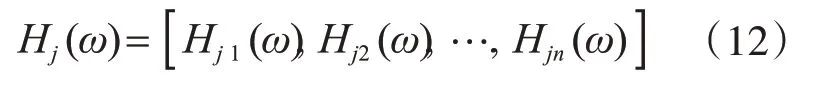
則有

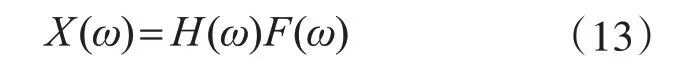
將式（13）代入式（10），得

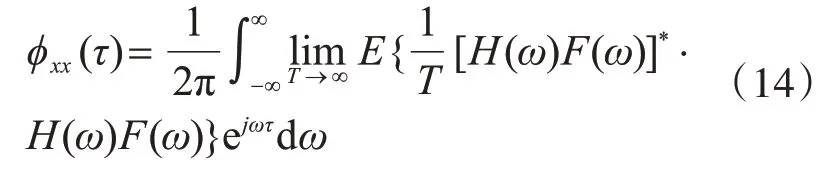
可見，在F(ω)一定的情況下，自相關函數φxx(τ)只與各激勵點之間的頻響函數H(ω)有關。因此，自相關函數幅值向量中的各分量元素具有固定的比例關系，也即是具有固定的形態。

2 木結構古建筑的結構特性

中國古建筑木結構有別于現代的鋼結構、鋼筋混凝土結構。尤其在結構抗震上，中國木結構古建筑體現出了“以柔克剛、摩擦耗能、滑移隔震”的抗震原則，是高度有機的結構體系。這與現代結構大多采用“加強結構、硬抗地震”的抗震原則有很大的不同［13］。

木結構古建筑在結構上最顯著的一個特點是梁柱等構件之間采用榫卯節點連接。榫頭和卯口間因摩擦滑移而具有耗能作用，這是木結構古建筑具有較好抗震性能的一個重要原因［14］。

方東平等［15］采用桿件單元和半剛性節點單元建立木結構古建筑的有限元模型，通過定義和引入反映古建筑木結構榫卯節點特性的半剛性節點單元，對榫卯節點的力學性能作了定量研究，證實了木結構古建筑的榫卯節點是半剛性的。

薛建陽［16］將榫卯的力學模型比擬為變剛度彈簧單元，進行了動力時程分析。結果表明：由于大震下柱底與礎石的滑移和榫卯與斗拱的摩擦阻尼作用，大幅度減少了上部結構的地震響應。因此，中國古建筑木結構具有良好的耗能與減震性能。

3 算例分析

3.1 有限元模型的建立

以西安鐘樓為工程背景，建立木結構古建筑有限元模型時，選取一榀木框架進行損傷識別分析。木梁長4 m，截面尺寸為300 mm×700 mm；木柱高6 m，截面直徑為500 mm，梁柱采用Beam188單元。基于榫卯節點的半剛性特點，采用Combin14 彈簧單元模擬梁柱的榫卯連接。每個節點共有六個自由度，其中三個平動自由度UX、UY、UZ 和三個轉動自由度ROTX、ROTY、ROTZ。榫卯節點剛度采用文獻［17］中根據鐘樓監測數據得到的近似值：1×1010kN·m/rad。木材的彈性模量為1×1010N/m2，泊松比為0.25，密度為410 kg/m3，采用Rayleigh定義的黏性比例阻尼。

木結構框架有限元模型及節點編號如圖1所示。

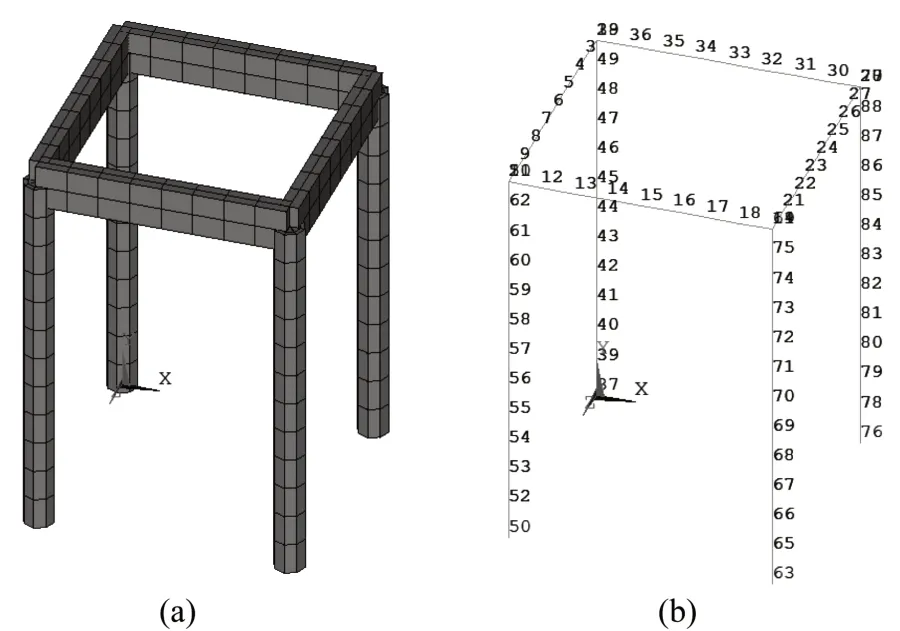
圖1 有限元模型（a）及節點編號（b）Fig.1 Finite element model and nodes number

韓廣森［18］利用列車荷載經驗分析模型，計算出了西安地鐵2 號、6 號線單線運行時的作用荷載，得到了不同速度下的荷載值，并通過MATLAB得到了激勵的時程曲線和頻譜曲線。將經過土層傳播折減后的激勵作用到鐘樓的有限元模型上，并對2 號、6 號單線運行下的鐘樓響應進行了分析。

本文在建立木框架有限元模型進行分析時，隨機激勵選擇西安地鐵單線運行時，速度分別為V1=20 km/h 和V2=40 km/h 時的荷載值作為隨機激勵樣本1 和隨機激勵樣本2 施加在柱腳節點上。激勵時長取T=12 s，時間步長為Δt=0.01 s。

3.2 結構的損傷識別

選取木框架上節點編號為1-9 的一跨梁進行分析。梁長4 m，網格劃分時單元大小取0.5 m，共8 個單元。由于建立有限元模型時梁兩端邊單元的節點與梁柱的榫卯節點重合，本文選取梁上中間6 個單元進行損傷識別與定位分析，單元編號為①-⑥，對應的節點編號為1-7。

首先對完好結構分別施加隨機激勵1 和隨機激勵2，提取完好結構在兩個隨機激勵下的兩組加速度動力響應。計算完好結構在兩個隨機激勵下的兩組自相關函數幅值向量分別為A1和A2，經歸一化后的兩條曲線如圖2所示。

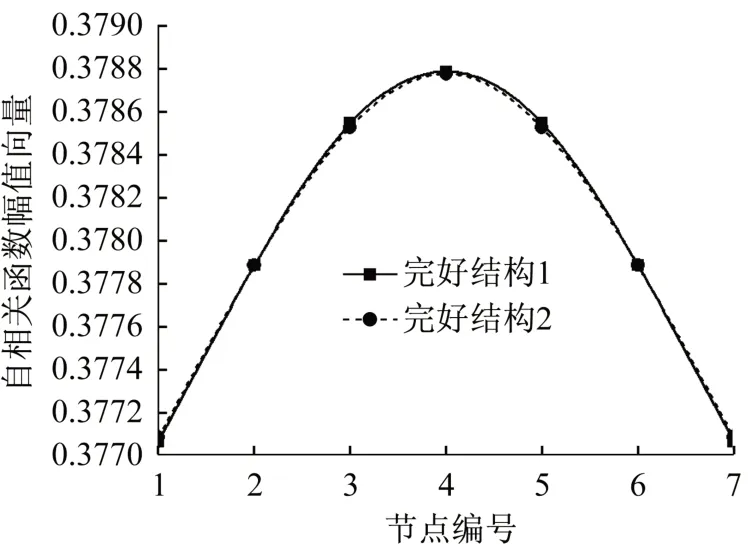
圖2 A1和A2的ACFA曲線Fig.2 ACFA curves of A1and A2

由圖可以看出，完好結構在兩個不同隨機激勵下的兩條自相關函數幅值向量曲線幾乎吻合。這說明對于隨機振動的結構，在結構完好狀態下，各測點動力響應的自相關函數幅值向量具有固定的形態。因此，可以采用隨機振動結構各測點動力響應的自相關函數幅值向量判別結構的損傷。計算圖中兩條自相關函數幅值向量曲線之間的互相關系數，如表1所示。

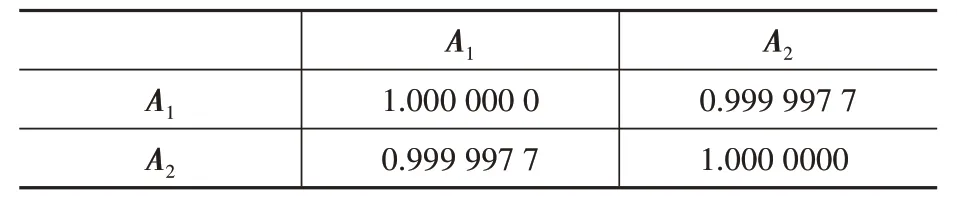
表1 A1和A2之間的互相關系數Table 1 Cross correlation coefficient of A1 and A2

將A1和A2之間的互相關系數ρ12=0.999 997 7作為損傷識別的基準值。若損傷結構的ACFA 與完好結構的ACFA 之間的互相關系數明顯小于該基準值，則認為結構發生了損傷。

通過降低梁單元的剛度模擬結構的損傷。以④單元為例，將單元④的剛度降低30%，提取結構損傷狀態下梁上各測點的加速度響應，并計算各測點加速度響應自相關函數的最大值δii，組成損傷結構的自相關函數幅值向量，記為Ad。損傷結構Ad與完好結構A1、A2的自相關函數幅值向量曲線如圖3所示。

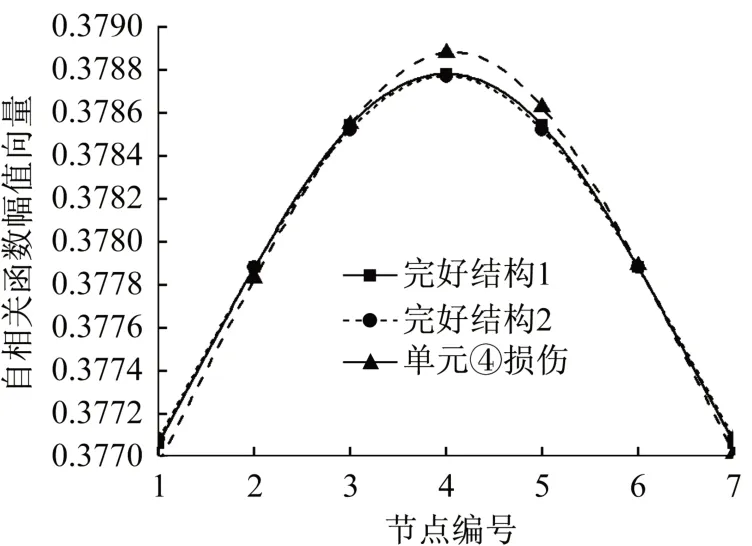
圖3 損傷結構與完好結構的ACFA曲線Fig.3 ACFA curves of A1、A2 and Ad

從圖中可以看出，單元④損傷時的自相關函數幅值向量曲線與完好結構A1、A2的曲線相比有明顯的波動。完好結構的自相關函數幅值向量曲線取為A1，即將A1記為Au。單元④損傷時，經計算，損傷結構Ad與完好結構Au之間的互相關系數如表2所示。

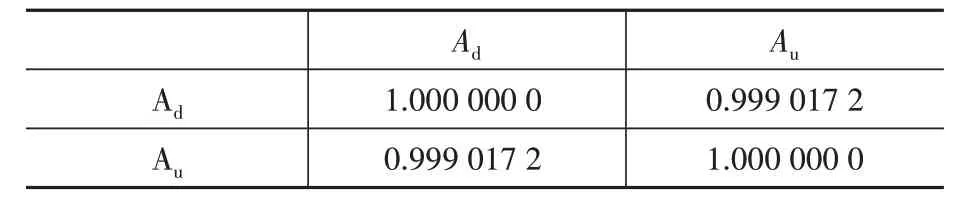
表2 Ad與Au之間的互相關系數Table 2 Cross correlation coefficient of Ad and Au

取ρdu=0.999 02。同樣的方法，可以計算出其他各單元分別發生損傷時，與完好結構之間的互相關系數，如表3所示。

表3 損傷結構與完好結構之間的互相關系數Table 3 Cross correlation coefficient of Ad and Au

將表中各單元損傷時的互相關系數與基準值做對比，可以發現，損傷結構與完好結構之間的互相關系數有明顯的降低，由此可以判斷結構發生了損傷。因此，使用結構損傷前后各測點自相關函數幅值向量之間的互相關系數作為損傷因子可以有效判別結構的損傷。

3.3 損傷定位分析

由前述損傷因子的變化可知，當結構發生損傷時，損傷結構與完好結構之間的相關性會降低，也即是損傷結構的自相關函數幅值向量曲線會發生波動。分別將各單元的剛度降低30%，繪制各單元發生損傷時與完好結構的自相關函數幅值向量曲線，如圖4所示。

從圖中可以看出，當結構發生損傷時，自相關函數幅值向量的曲線會發生波動。梁兩端邊單元損傷時，各測點自相關函數峰值的波動較小；中間單元損傷時，梁上各測點自相關函數的峰值波動幅度較大，從而導致結構損傷前后自相關函數幅值向量之間的相關性降低。

為了衡量損傷前后曲線的波動程度，計算各測點損傷前后峰值的變化率，即：

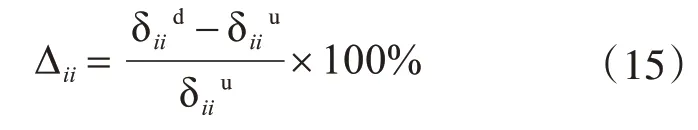
當各單元分別發生損傷時，梁上各測點自相關函數峰值損傷前后的變化率如圖5所示。

從圖中可以看出，當梁上某一單元發生損傷時，該單元的兩個節點的峰值變化率最大。如單元②損傷時，損傷前后相鄰的兩個節點2和3的峰值變化率最大，此時對應著單元②兩端的兩個節點。其他單元分別損傷時，也滿足這種對應關系。所以，可以利用結構損傷前后各測點峰值變化率的最大絕對值來確定結構的損傷位置，即結構損傷后峰值變化率最大的相鄰兩個節點的區域對應著結構的損傷單元。

由于信號自身與自身的強相關性，使用各測點的自相關函數幅值向量比兩點之間的互相關函數幅值向量能更明確表達結構損傷前后峰值的變化程度，不需要再對各測點的相對變化進行二次差分，進而避免了由于二次差分造成的節點與單元的位置偏移，使損傷前后各測點峰值的相對變化更加突出，識別結果更加突出明顯。

3.4 測量噪聲對損傷識別的影響

為了模擬實際工程中噪聲對測量信號的影響，向節點加速度中分別加入信噪比SNR=20 db、10 db、0 db 的高斯白噪聲。分別計算不同噪聲水平影響下，結構損傷前后各測點自相關函數峰值的變化率。為了方便對比，將無噪聲和三組不同噪聲水平的自相關函數峰值的變化率歸一化，如圖6所示。

從圖中可以看出，單元③損傷時，無噪聲情況下，單元的兩個節點3和4的峰值變化率明顯高于其他各測點，能夠準確進行損傷定位。隨著信噪比的降低，其他各測點的峰值變化率逐漸接近損傷單元的兩個節點峰值變化率的數值，但當SNR=0 dB時，仍能對損傷單元③進行準確定位。因此，對于受隨機振動的結構，采用各測點損傷前后自相關函數峰值的變化率作為損傷定位指標具有較好的抗噪聲干擾能力。

4 結 論

通過降低各單元的剛度模擬結構的損傷，利用結構損傷前后各測點自相關函數幅值向量之間的互相關系數和損傷前后各測點的峰值變化率對古建筑木結構進行損傷識別和定位，結果表明：

（1）以結構損傷前后各測點自相關函數幅值向量之間的互相關系數ρ作為損傷因子能有效識別結構的損傷。

（2）計算結構損傷前后各測點自相關函數峰值的變化率，變化程度最大的相鄰兩個測點分別對應著損傷單元的兩個節點，說明使用各測點自相關函數的峰值變化率能準確確定結構的損傷位置。

（3）當信噪比SNR=0 dB 時，仍然能較準確的確定結構的損傷位置，損傷定位指標不受測量噪聲的影響。因此，采用結構損傷前后各測點自相關函數峰值的變化率作為損傷定位指標，具有較好的抗噪聲干擾能力。

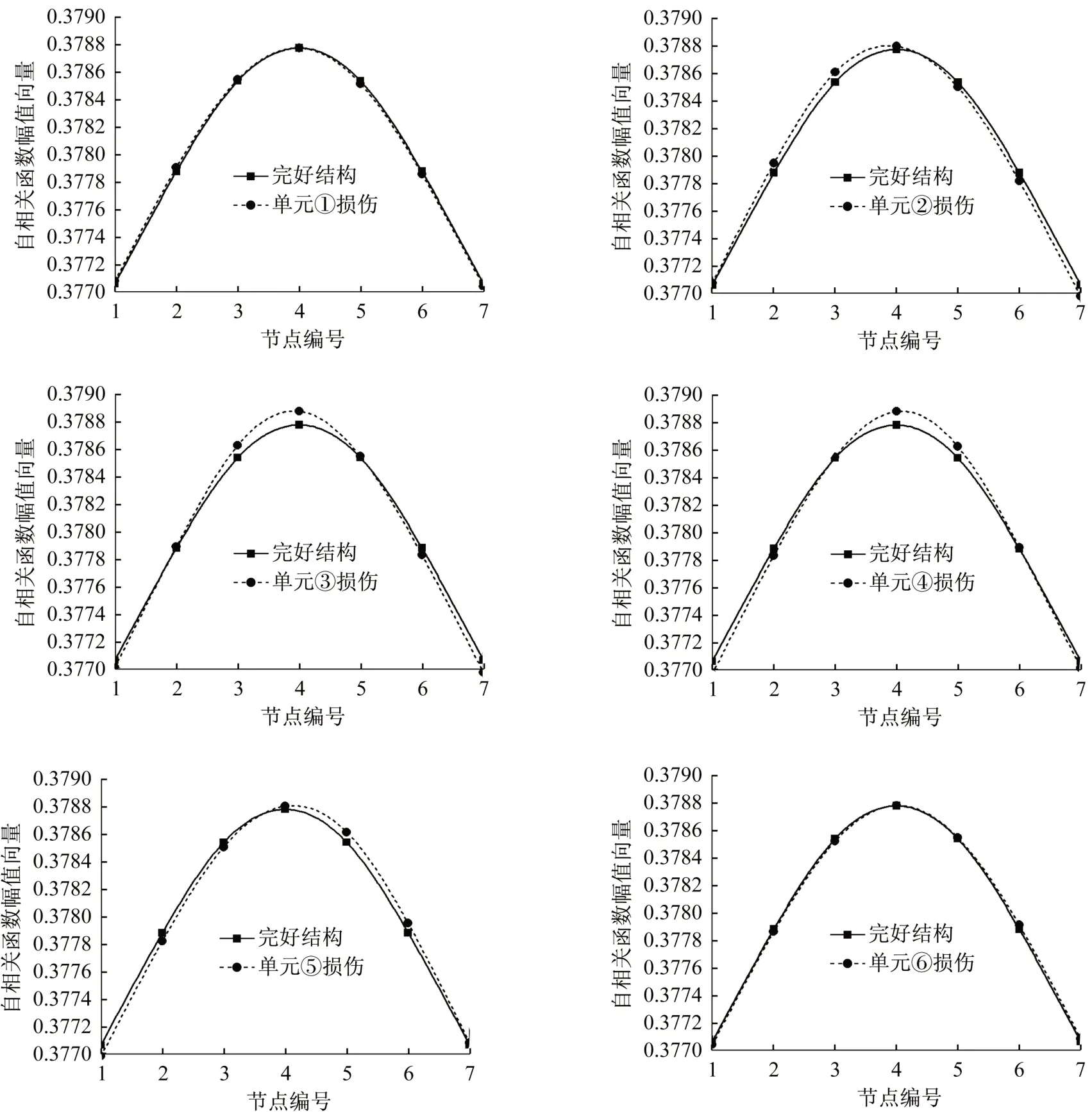
圖4 各單元損傷時與完好結構的ACFA曲線Fig.4 ACFA curves of Ad and Au

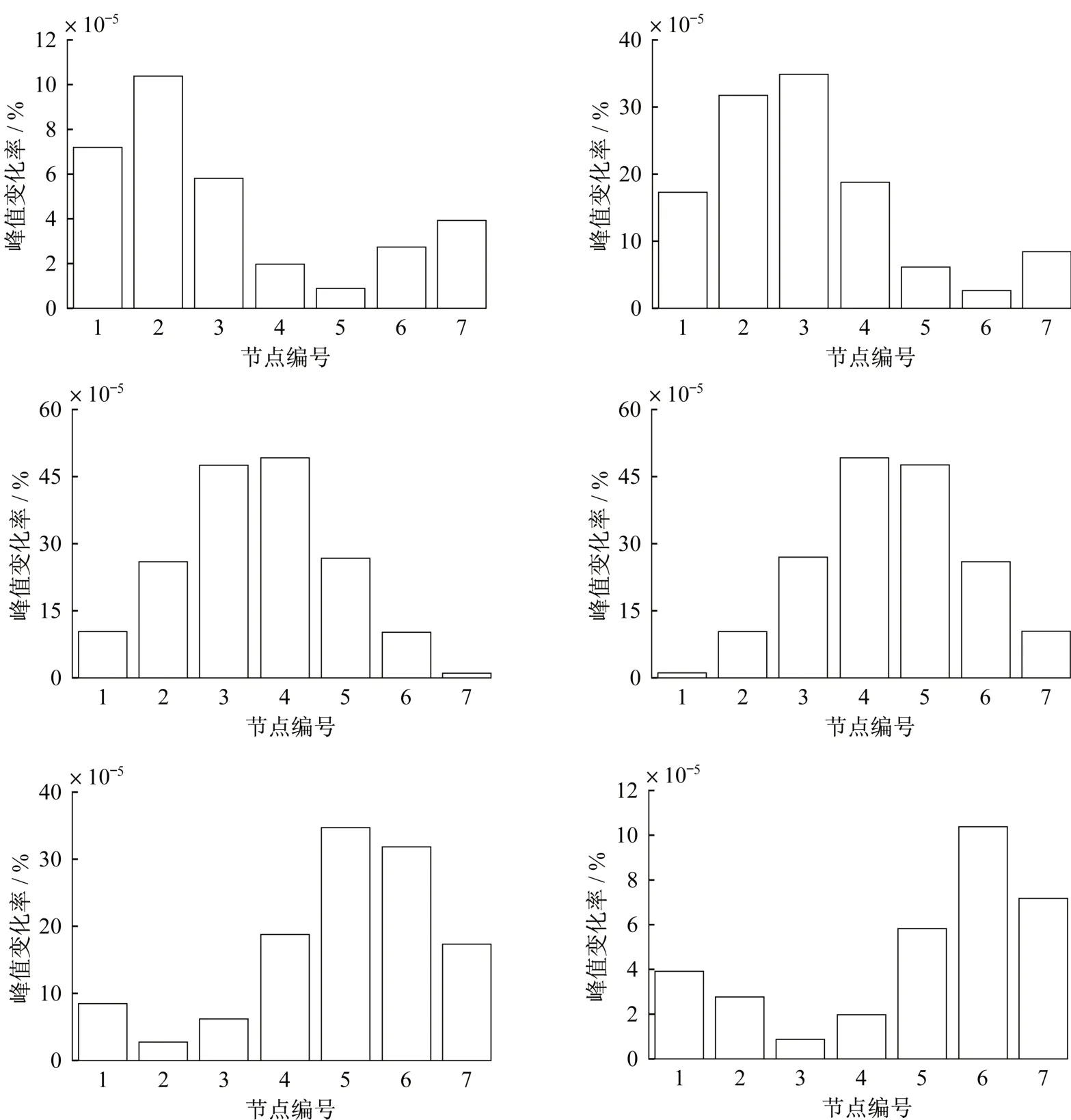
圖5 損傷前后各測點峰值變化率Fig.5 Change rate of peaks between Ad and Au

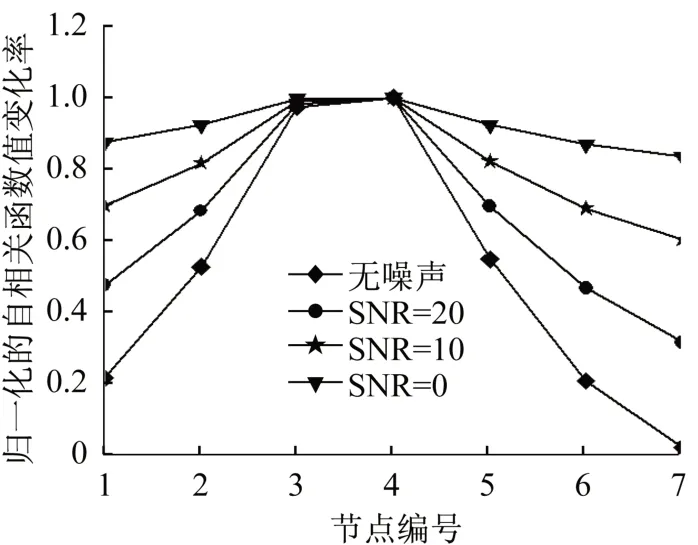
圖6 不同噪聲水平下單元③的損傷定位Fig.6 Damage location at different noise levels