大型天線舉升機構的運動學仿真分析

張旭東，閆秀峰

(中國電子科技集團公司第五十一研究所，上海 201802)

0 引 言

在現代高科技戰爭背景下，提高車載電子裝備的機動性是確保電子裝備生存能力的有效手段之一。

影響車載電子裝備機動性的主要是裝備的架設和撤收時間、裝備的快速轉移能力和載車的越野能力。本文重點探討的是裝備架撤時間，尤其對于大型自動折疊天線，其快速架設和撤收性能將直接影響設備的效能發揮。

本文主要以一種大型拋物面天線的舉升機構為研究對象。由于拋物面天線體積大、重量重，舉升到既定角度時突然停止，會產生很大的沖擊力。因此，舉升機構的速度既不能過快，也不能過慢，速度太快將會損壞天線設備；速度太慢又會影響設備架設和撤收的時間要求。為解決這一問題，利用Solidworks Motion仿真模塊，對天線舉升機構的速度和加速度進行運動仿真分析。結合力學分析結果，獲得舉升機構在展開過程中的最佳運動時間。

1 天線舉升機構仿真分析

1.1 機構型式及運動過程

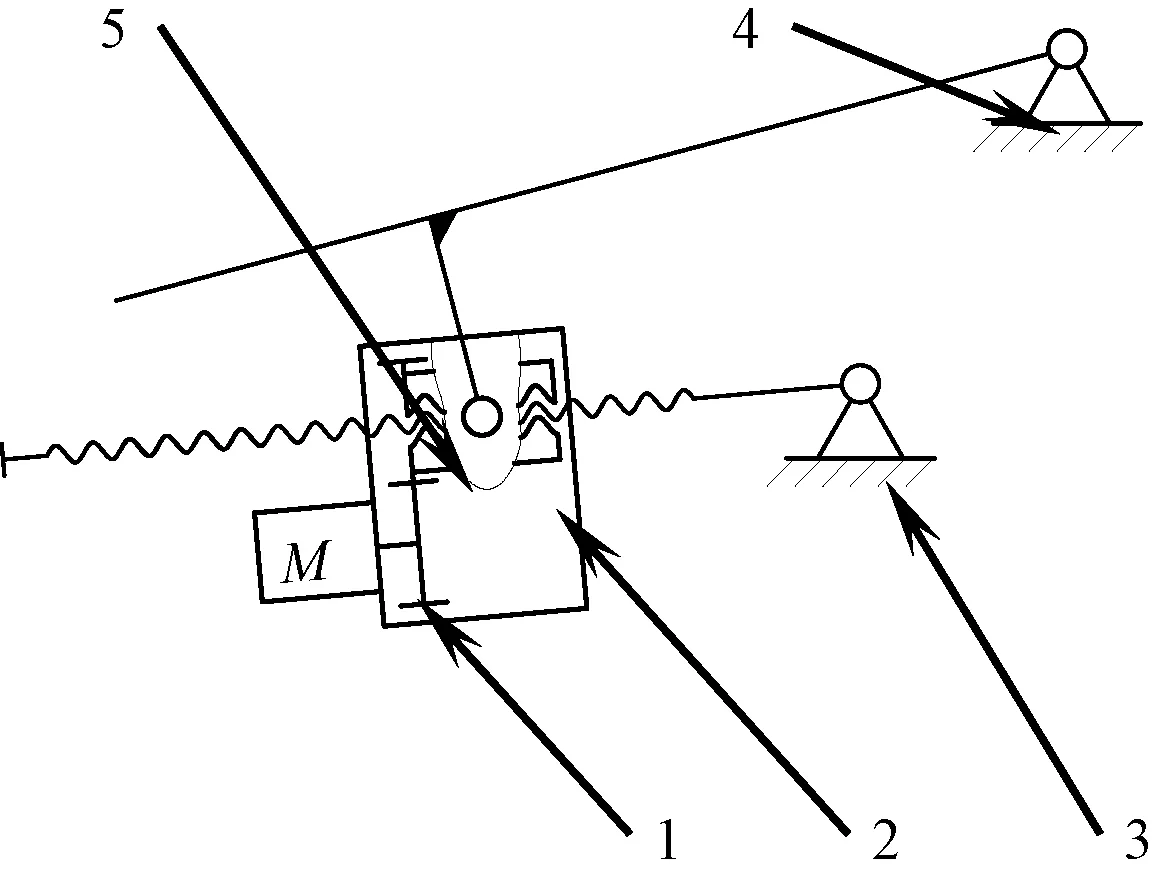
拋物面天線在運輸狀態下，平放在設備平臺上；天線舉起時，由伺服電機帶動天線背面的滾珠絲杠運動，根據連桿原理，天線骨架將會繞轉軸旋轉，逐漸翻起至工作狀態；當到達既定位置時突然停止，進入工作狀態。舉升機構展開過程示意圖如圖1所示。

1—天線骨架；2—支撐架；3—舉升絲桿；4—驅動電機；5—傳動裝置圖1 舉升機構展開過程示意圖

1.2 運動分析的理論依據

要分析力和運動之間的關系，可以采用拉格朗日乘數法。首先,根據舉升過程建立拉格朗日運動方程[1]:

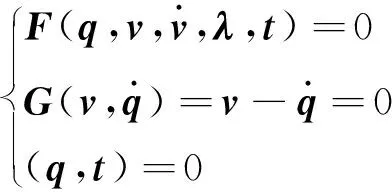
(1)

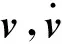
運動學分析主要研究零自由度系統的位置、速度、加速度和約束反力，因此只需求解系統的約束方程：

φ(q,t)=0

(2)

式中：φ為描述完整約束的代數方程列陣。

上式可以用Gear預估-校正算法進行求解。根據當前時刻的系統狀態矢量值，取時間步長h=tn+1-tn，用Taylor級數預估下一個時刻系統的狀態矢量值[2]：

(3)

當得到的新時刻的系統狀態矢量值不準確時，約束方程不等于零，可由GearK+1階積分求解程序來校正：

(4)

式中：yn+1為y(t)在t=tn+1時的近似值；β0，ai為積分程序的系數值。

對式(4)進行變形得：

(5)

式(2)在t=tn+1時刻應有：

φ(qn+1,tn+1)=0

(6)

在任意時刻tn的位置由約束方程的Newton- Raphson迭代方法進行求解：

(7)

式中：Δqj=qj+1-qj，j表示第j次迭代。

在任意時刻tn的速度、加速度，由約束方程求一階、二階時間導數得：

(8)

(9)

在任意時刻tn的約束反力由拉格朗日方程乘數法得到：

(10)

根據以上原理，調用Solidworks Motion模塊，對各機構進行自由度限制，定義原動件的函數和步長，即可自動記錄各構件的運動軌跡、位置參數、角速度、角加速度和力等相關信息。

1.3 建立運動算例

創建一個運動算例，并為該運動算例創建了支撐架、滾珠螺母、天線骨架、驅動電機和舉升絲桿5個零部件。支撐架為靜止零部件，滾珠螺母、天線骨架、驅動電機和舉升絲桿為運動零部件。

舉升機構共有5組運動關系副:齒輪與齒輪嚙合的齒輪副；滾珠螺母繞滾珠絲桿旋轉的螺旋副；滾珠絲桿繞支撐架旋轉的轉動副；天線骨架繞滾珠裝置旋轉的轉動副；天線骨架繞支撐架旋轉的轉動副。舉升機構運動機構簡圖如圖2所示。

1—齒輪副；2—螺旋副；3、4、5—轉動副圖2 舉升機構運動機構簡圖

1.4 定義運動函數

舉升機構的原動件為驅動電機，驅動電機通過齒輪副帶動滾珠螺母以恒定轉速轉動，轉速可以通過函數來表示原動件的運動規律。因此為齒輪副的驅動函數設定為等速，并設置轉數，齒輪副的驅動設置如圖3所示。滾珠絲杠的導程為10 mm，定義滾珠絲桿和滾珠螺母的螺紋節距，即滾珠螺母每轉一圈所移動的距離為10 mm。

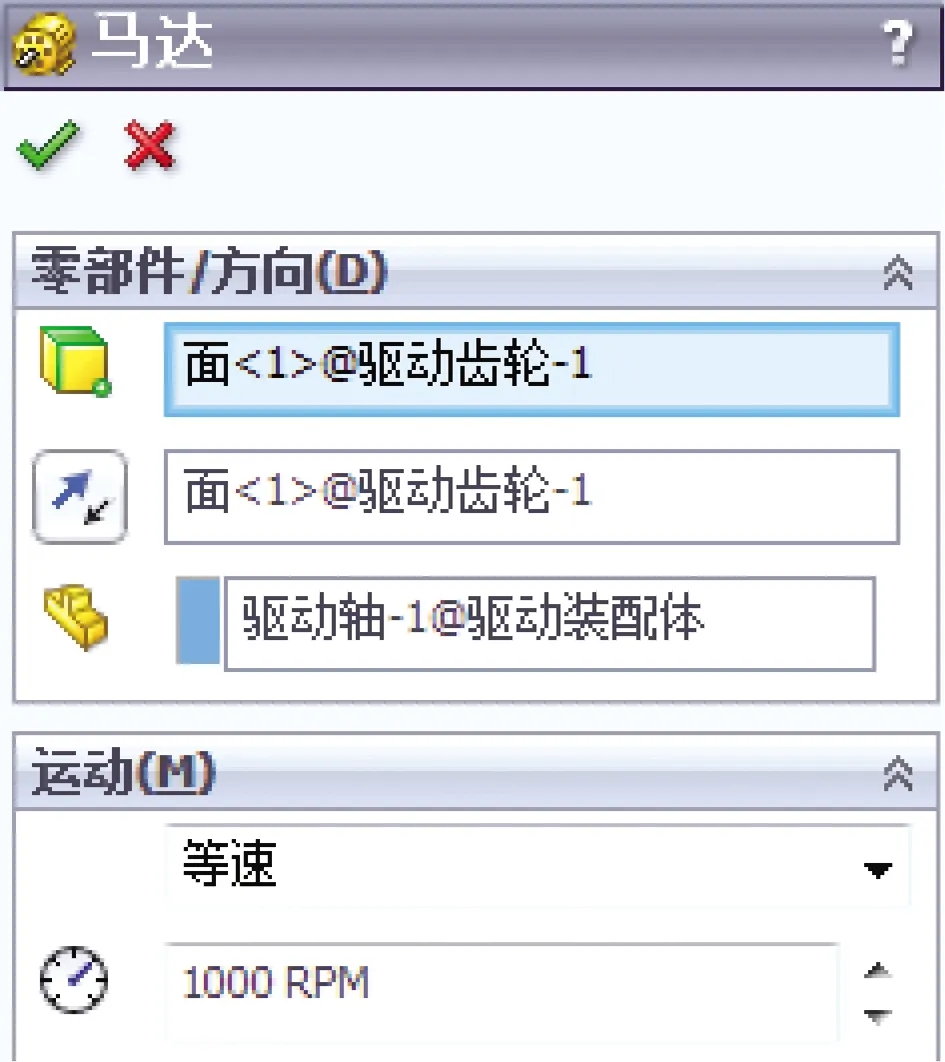
圖3 齒輪副的驅動設置

2 求解與仿真結果分析

2.1 機構求解

根據給定的函數和步長，自動記錄各構件的運動軌跡、位置參數、角速度和角加速度等信息[3]。

根據架設和撤收時間要求，首先選擇舉升機構從運輸狀態到舉升到位狀態總運動時間為180 s，對舉升機構進行運動仿真分析，角速度和角加速度的響應函數圖如圖4和圖5所示。從2張圖的曲線可知，當運動時間持續180 s，角速度和角加速度最大位置均出現在架設完畢時。要使舉升機構到位沖擊小、架設時間短，就需通過分析求出最佳運動時間。

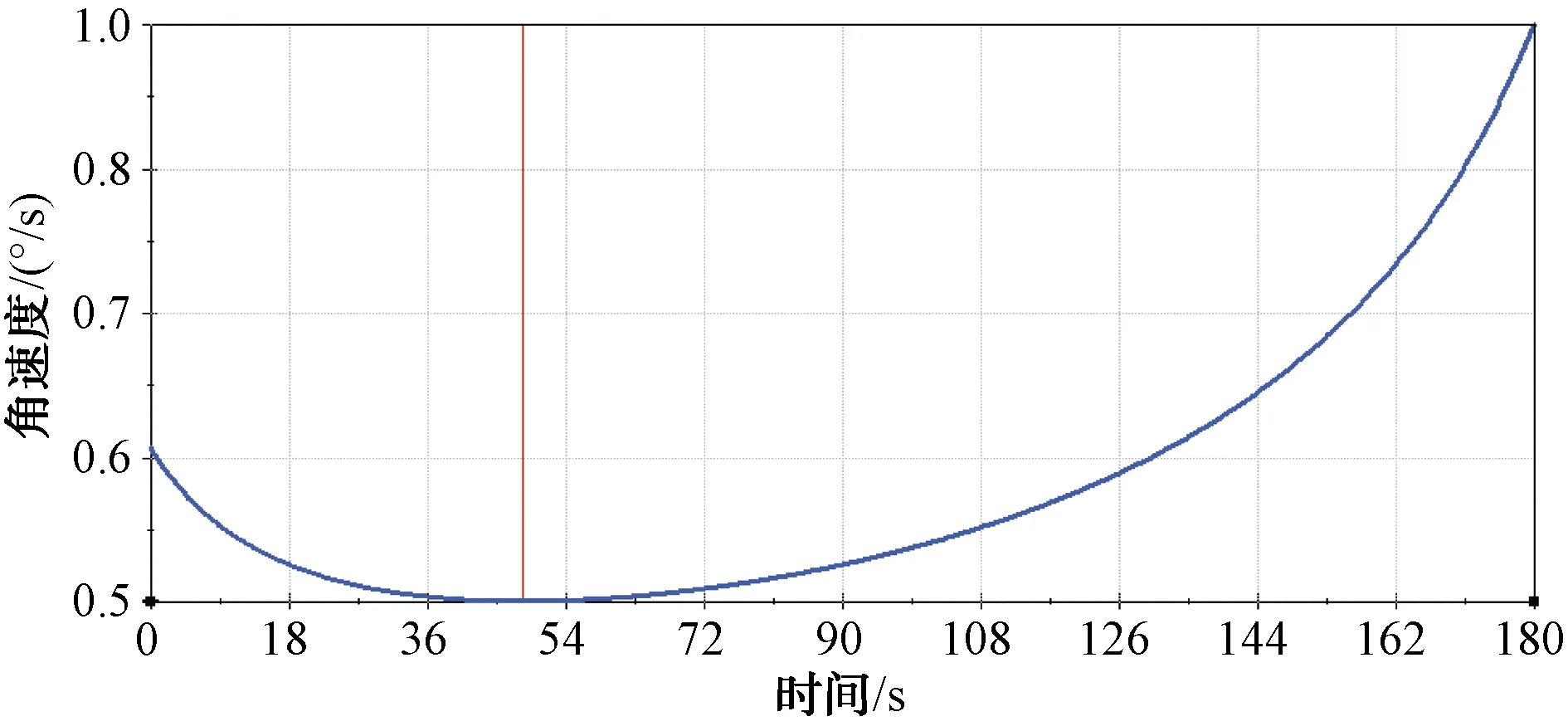
圖4 角速度的響應函數圖

圖5 角加速度的響應函數圖

2.2 機構簡化力學分析及計算

舉升機構架設完成時，天線到位的狀態如圖1所示，將天線骨架近似簡化為均質細長直桿OA，簡化圖見圖6。Moq是慣性力系主矩；N是作用在天線質心上的拉力；FF是天線口面受到12級風時的風力[4]。驅動電機的加速和減速過程所需的時間均為t=0.3 s。

圖6 天線力學分析簡化圖

研究對象為桿OA。向O點簡化桿件的慣性力系，可得到[5]：

(11)

由動靜法可知：∑Mo=0。

即:

(12)

根據動量定理：

-Ft=mv2-mv1

(13)

式中：F為作用在質心上的沖擊力；v1為初速度，v1=ωR；v2為末速度，v2=0。

由式(13)可得：

(14)

為使舉升機構運動平穩，沖擊力盡量小，應滿足關系式N>F，化簡得：

(15)

風力的計算公式為：

(16)

式中：v為風速(取值35 m/s)；ρ為空氣密度(計算時取ρ=0.125 kg/m3)；A為天線特征面積(取值13.3 m2)；CF為風力系數，查詢取值1.3。

經計算得：FF=12 951.9(N)。

已知，R=2 200 mm；θ=10°，將各數值代入式(15)，得：

ω<0.93+0.4ε

(17)

2.3 結果分析

天線舉升機構運動過程中，角加速度趨近于零時，機構所受的沖擊力也趨近于零，由式(17)可知，當ε=0時，ω<0.93，因此選擇角速度接近0.93°/s的數據進行記錄。按照時間間隔為5 s的運動時間函數進行仿真求解，并記錄最后一刻的角速度和角加速度。數據如表1所示。

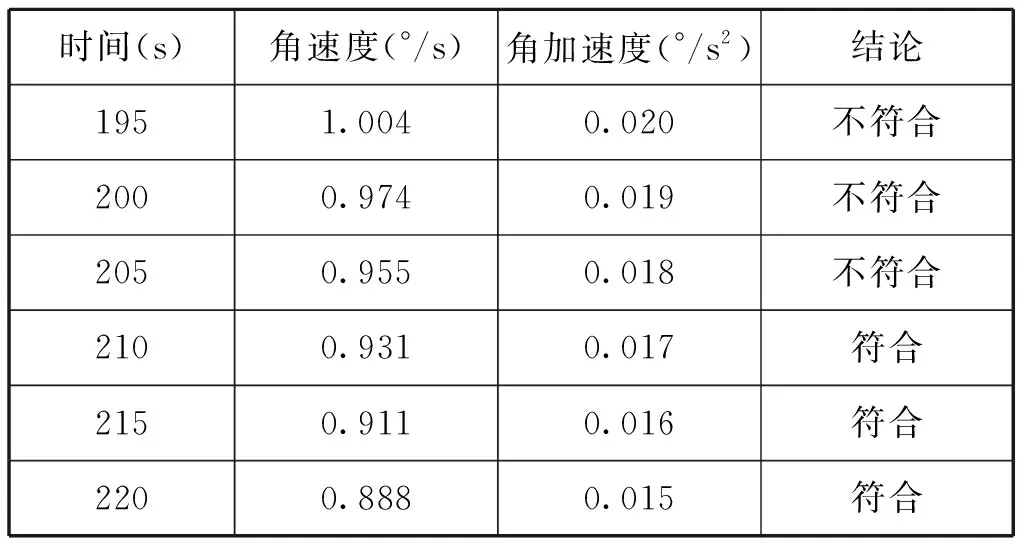
表1 角速度和角加速度數據表

將表1中的數值分別代入式(17)中，運動時間為210 s以上滿足要求，取其中運動時間最短的(即運動時間為210 s)，滿足天線舉升機構既能快速展開到位又不產生較大的運動沖擊的要求。角速度和角加速度的響應函數圖如圖7和圖8所示。

圖7 角速度的響應函數圖

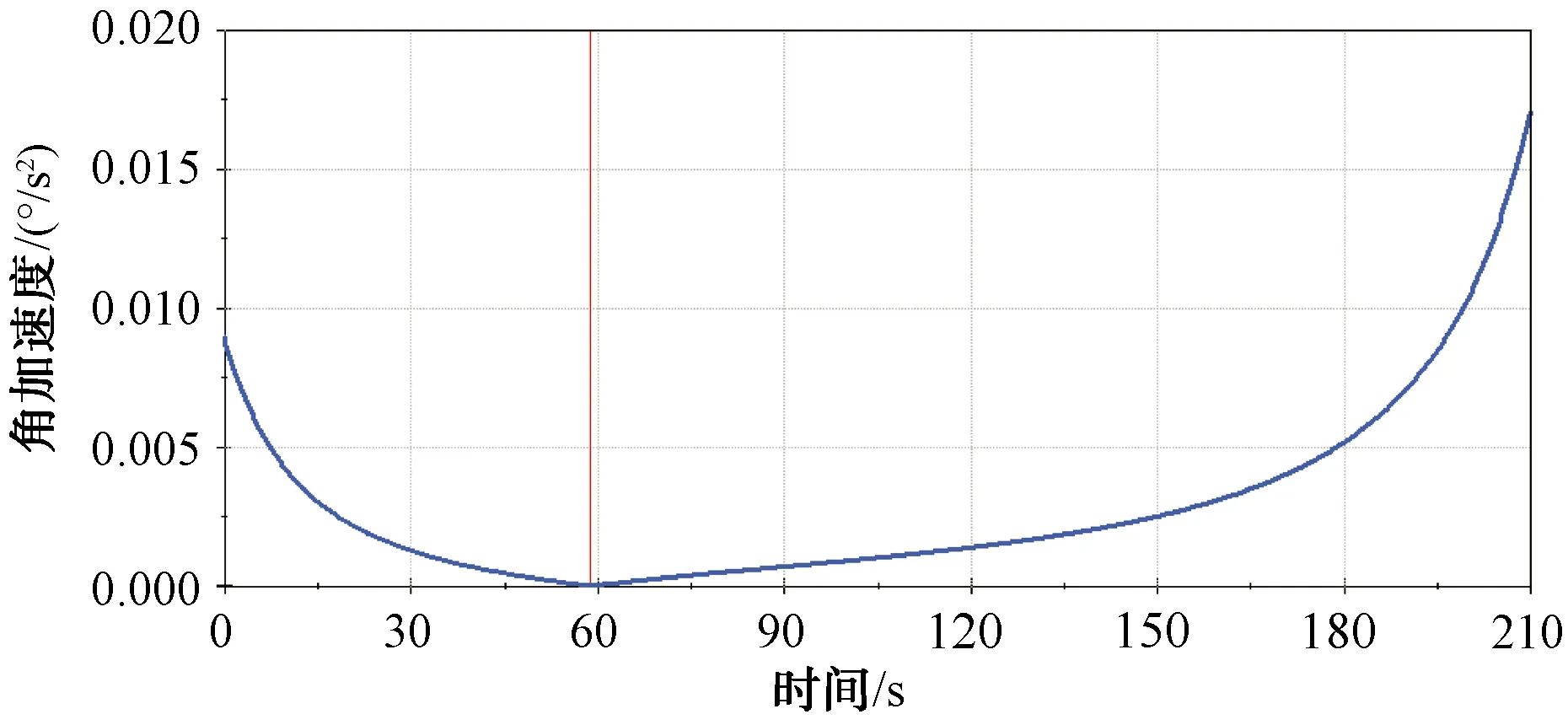
圖8 角加速度的響應函數圖

3 結束語

根據不同的運動時間函數，得到了天線舉升機構的角速度和角加速度響應函數圖。在減小運動沖擊、提高設備機動性的前提下，通過力學分析尋求機構的最佳運動時間。按照運動時間為210 s的指標設計，天線舉升機構使用效果良好，驗證了該運動仿真分析和方法的可行性。