基于導彈預警功能建模的預警參數分析

郭 旭，陸 港，周 瀟

(空軍預警學院，湖北 武漢 430019)

0 引 言

彈道導彈預警是戰略反導作戰的前提，其發展水平關乎國家命脈，因而受到了廣泛重視。由于起步較早，國外軍事強國的預警體系建設已較為完善，具備了很強的預警探測能力[1-2]。要對導彈的預警過程及預警參數進行分析，需要使用多種專業功能突出的仿真軟件[3]。其中STK功能強大，可用于航天、情報、雷達、電子對抗、導彈防御等各方面[4-5]。我國目前已經開始彈道導彈預警體系的開發，但由于起步較晚，很多技術尚處于起步階段，還需要很多探索。

探索研究預警參數與導彈各項預警參數之間的關系，從而找到最合理的優化配置方法，選擇合理的探測精度，得到最為優化的預警結果，在一定程度上可以提高導彈預警系統的總體設計質量，為今后導彈仿真優化設計以及對我國的彈道預警體系提供參考。

1 導彈落點預報及誤差分析

通過衛星觀測導彈，并將信息提供給雷達，雷達就能對目標導彈進行觀測，得到目標導彈在一段時間內的位置、速度信息。根據這些信息，就可以對目標導彈的落點進行預報。

1.1 航天器坐標系簡單介紹

為了描述運動點的規律，確定點在空間中的位置，必須確定恰當的坐標系，包括確定坐標原點、參考平面和參考平面上的主方向3個要素。這里首先對常用的坐標系進行以下簡單介紹：

(1) 地心慣性坐標系OeXIYIZI

地心慣性坐標系是一個慣性參考基準，用來描述航天器在慣性空間中的絕對運動。地心慣性坐標系OeXIYIZI的3個要素定義如下：

(a) 坐標原點為地球質心。

(b) 參考平面OeXIYI為地球赤道面。

(c) 參考平面上的主方向：OeXI軸指向春分點方向；OeZI軸與地球南北軸重合，指向北極；OeYI軸與OeXI軸和OeZI軸構成右手坐標系。

(2) 地心固連坐標系OeXEYEZE

地心固連坐標系是隨地球一同轉動的動參考基準，用以描述航天器相對地球的視運動，即航天器相對地球的相對運動。地心固連坐標系OeXEYEZE的3個要素定義如下：

(a) 坐標原點Oe為地球質心。

(b) 參考平面OeXEYE為地球赤道面。

(c) 參考平面上的主方向：OeXE軸在赤道面指向格林尼治子午線(零子午線)方向；OeZE軸與地球南北軸重合，指向北極；OeYE軸與OeZE軸構成右手坐標系。

(3) 導彈發射極坐標系o1x1y1z1

導彈極坐標系是以導彈的發射點為參考點，用來描述導彈相對與發射點的視運動。導彈極坐標系o1x1y1z1的3個要素定義如下：

(a) 坐標原點o1為導彈在地球表面的發射點。

(b) 參考平面為與發射點所在位置相切的平面。

(c) 參考平面上的主方向：o1y1指向導彈的發射方向；o1x1與o1z1構成右手坐標系。

(4) 瞬時地心坐標系oxyz

瞬時地心坐標系也稱為真地球坐標系，它的3個要素定義如下：

(a) 坐標原點位于地球質心。

(b) 參考平面OeXEYE為地球赤道面。

(c) 參考平面上的主方向：oz軸指向瞬時地球自轉軸方向，ox軸指向瞬時赤道面和包含瞬時地球自轉軸與平均天文臺參考點的子午面的交點。

(5) J2000慣性坐標系oAxAyAzA

由于恒星赤經和赤緯會因歲差(與恒星的自行)改變，所以天文學家們經常指定某一特定的紀元作參考點。J2000坐標系是指由J2000時刻的天赤道與二分點來定義天球參考坐標系。它是在天文學上使用的歷元，前綴“J”代表這是一個儒略紀元法，它指的是儒略日期TT時2 451 545.0，即相對于世界協調時間2000年1月1日11∶58∶55.816。

1.2 常見坐標系之間的轉換

1.2.1 地心慣性坐標系、地心固連坐標系之間的轉換

航天器在地心慣性坐標系OeXIYIZI和地心固連坐標系OeXEYEZE的三維位置表示是不相同的，但可以相互轉換。2種坐標系的原點以及OeZI軸與OeZE軸始終是重合的，地心固連坐標系OeXE軸和OeYE軸卻始終繞地球南北軸轉動，而地心慣性坐標系在慣性空間中固定不動。如果知道某初始時刻t0地心固連坐標系的OeXE和地心慣性坐標系OeXI軸之間的夾角θ=θ0+Ωe(t-t0)，Ωe為地球自轉速度，其值約為7.292 115 ×10-5rad/s。

設在t0時刻之后的任意時刻t，航天器在地心慣性坐標系和地心固連坐標系中的三維位置用直角坐標表示分別為(xI,yI,zI) 和(xE,yE,zE)，兩者之間可以采用下式進行相互轉換，即：

(1)

式中：θ為此時刻地心固連坐標系的OeXE軸與地心慣性坐標系的OeXI軸之間的夾角。

1.2.2 地心固連坐標系OeXEYEZE與極坐標o1x1y1z1的轉換

極坐標系轉換到地心固連坐標系，可以先把極坐標系o1x1y1z1轉換到地心慣性坐標系OeXIYIZI，然后再把地心慣性坐標系OeXIYIZI轉換成地心固連坐標系OeXEYEZE。

1.3 導彈落點預報算法

1.3.1 將雷達探測到的導彈數據進行坐標系轉換

(1) 導彈極坐標系o1x1y1z1轉換到導彈發射坐標系oxyz

利用STK生成的導彈彈道選擇2個時刻TQ和TP，記錄2個時刻下對應的雷達測量的導彈參數[6](方位角αQ、αP,俯仰角βQ、βP,徑向距離rQ、rP)，這實際上相當于導彈在發射極坐標系下的坐標(αQ,βQ,rQ)、(αP,βP,rP)。

通過坐標系轉換，可以得到導彈在發射坐標系oxyz下的坐標(xQ,yQ,zQ)、(xP,yP,zP)。坐標系轉換過程如下：xQ=rQcosβQcosαQ,yQ=rQsinβQ,zQ=rQcosβQsinαQ;xP=rPcosβPsinαP,yP=rPsinβP,zP=rPcosβPsinαP。

(2) 導彈發射坐標系oxyz轉換到地心坐標系OeXEYEZE

得到導彈在發射坐標系oxyz下的2點的坐標(xQ,yQ,zQ)及(xP,yP,zP)后，繼續進行坐標系轉化，得到這2點在地心坐標系OeXEYEZE下的坐標。這2個坐標系的轉化方法如下：

這里已知雷達地理坐標(λ0,φ0,h)，其中λ0是雷達方位角，φ0是雷達的俯仰角，h是雷達的高度。坐標系的關系如圖1所示。

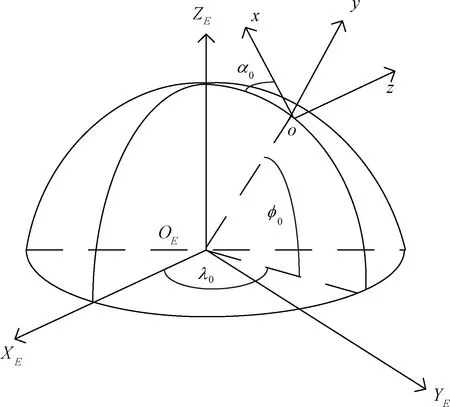
圖1 坐標系轉換示意圖

根據圖1，可以得到2個坐標系之間的轉化關系：

(2)

GE=M2[-(90°+α0)]M1[φ0]M3[λ0-90°]

(3)

這樣就得到了導彈在地心坐標系下的坐標。

(3) 地心慣性坐標系OeXIYIZI轉換成地心固連坐標系OeXEYEZE

將地心坐標系下的坐標(XE,YE,ZE)轉換到發射瞬時地心坐標系下(XI,YI,ZI)，坐標轉化公式為：

(4)

IE=M2[ΩG+we·t]·M3[ΩG]

(5)

這樣就得到了導彈在發射瞬時坐標系下的坐標。

最終要將發射瞬時地心坐標系下的坐標(XI,YI,ZI)轉換到地心慣性坐標系J2000下(XJ,YJ,ZJ)，轉換過程需考慮地球自轉與攝動的影響。

1.3.2 彈道導彈落點預報算法

首先以彈道所在平面為坐標平面，以地球球心O(橢圓軌道1個焦點)為坐標原點，以長軸所在直線為Yd軸建立彈道平面坐標系，P、Q兩點為導彈飛行過程中的兩點，B為導彈落點，如圖2所示。

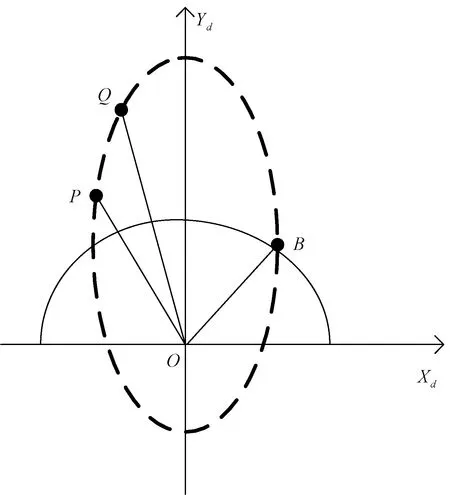
圖2 導彈飛行模型

根據STK直接讀出P、Q兩點的vP,vQ及rP,rQ，計算相關軌道根數和P、Q點坐標，計算步驟如下：

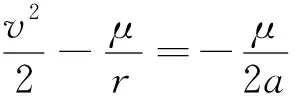
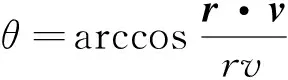
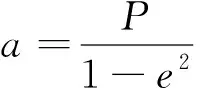
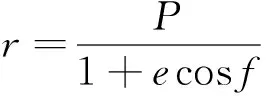
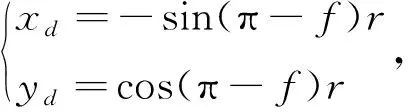
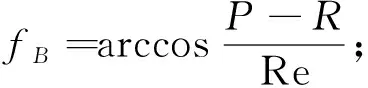
計算導彈在J2000坐標系下落點時，利用線性空間內積不變原理：

(6)

上式可簡化為：

(7)

將對應的坐標代入，會發現上式是一個關于(x1,y1,z1)的三元二次方程，求解即可得到導彈在J2000坐標系下的落點坐標(x1,y1,z1)。

2 導彈飛行時間的計算及誤差分析

2.1 導彈飛行時間的計算模型

首先以彈道所在平面為坐標平面，以地球球心O(橢圓軌道一個焦點)為坐標原點，以長軸所在直線為Yd軸建立彈道平面坐標系，Xd軸為與Yd軸垂直的坐標軸。A為導彈發射點，B為導彈彈著點，如圖3所示。

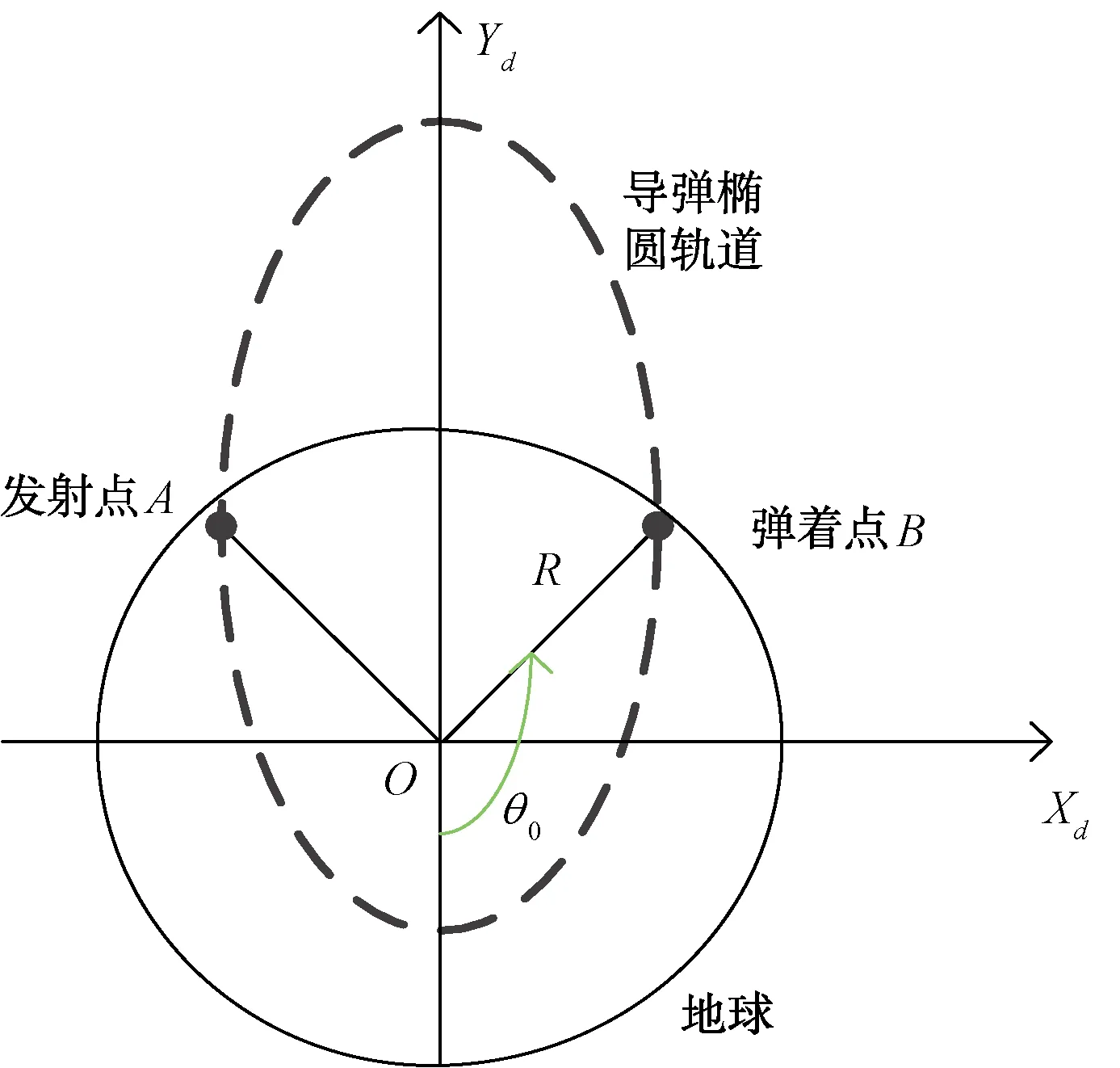
圖3 導彈飛行時間計算模型

根據STK直接讀出B點的vB及rB，計算B點對應的真近點角，計算過程如下：

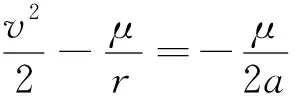
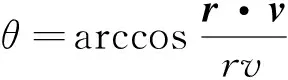
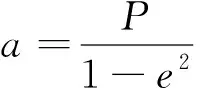
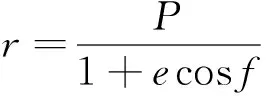
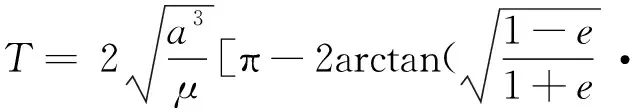
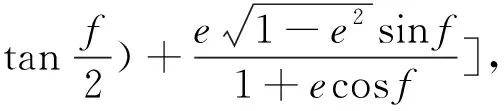
2.2 導彈飛行時間算法的穩定性及有效性仿真分析

以上是在理想狀況下，之后對vP,vQ及rP,rQ分別引入均值為0的高斯白噪聲。進行100次獨立重復試驗，計算出每次試驗對應的落點,預報平均值和均方根誤差，并畫出對應曲線。

2.2.1 仿真分析流程

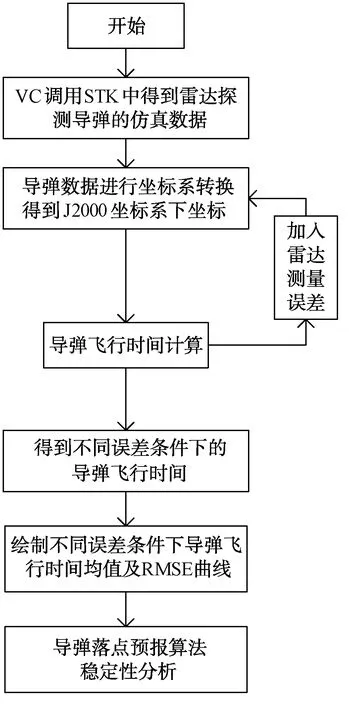
圖4 導彈飛行時間算法流程圖

導彈飛行時間算法的穩定性仿真驗證步驟如圖4所示,主要包括以下步驟：

(1) 利用STK進行雷達探測導彈仿真，得到導彈在飛行過程中每一時刻的位置、速度信息。

(2) 通過坐標系轉換，將導彈在極坐標系下的位置信息轉化到J2000坐標系下。

(3) 調用向量內積不變算法，進行導彈落點預報。

(4) 在雷達的探測數據中引入測量誤差，并在不同測量誤差等級下進行多次獨立重復試驗，求得各噪聲等級下落點預報均值和均方根誤差。

(5) 繪制曲線圖。

(6) 分析落點預報算法對于測量誤差的穩定性。

2.2.2 對導彈的位置測量數據加入誤差，驗證算法

首先在導彈的位置測量信息中加入均值為0、方差為σ=0∶50∶500的高斯白噪聲，進行100次獨立重復試驗，計算出每次試驗對應的落點預報平均值和均方根誤差，并畫出對應曲線，結果如圖5所示。

圖5 加入速度測量誤差后的導彈飛行時間預測效果圖

通過圖6可以看出，加入均值u=0、方差為σ=0∶50∶500(單位m)的位置測量誤差后，導彈預測飛行時間的均值比較穩定，變化不大，說明飛行時間的預測值對位置測量的穩定性較好。

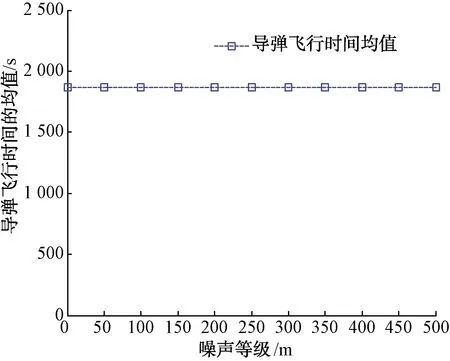
圖6 加入速度測量誤差后的導彈飛行時間均值

通過圖7可以看出，導彈預測飛行時間的均方根誤差(RMSE)并未隨著誤差等級σ的增大而增大，穩定在5 s附近，整體波動幅度較小，說明位置測量誤差對導彈飛行時間的預測影響較小。對于導彈飛行時間的預測，實際應用中可以放寬對導彈位置測量精度的要求。

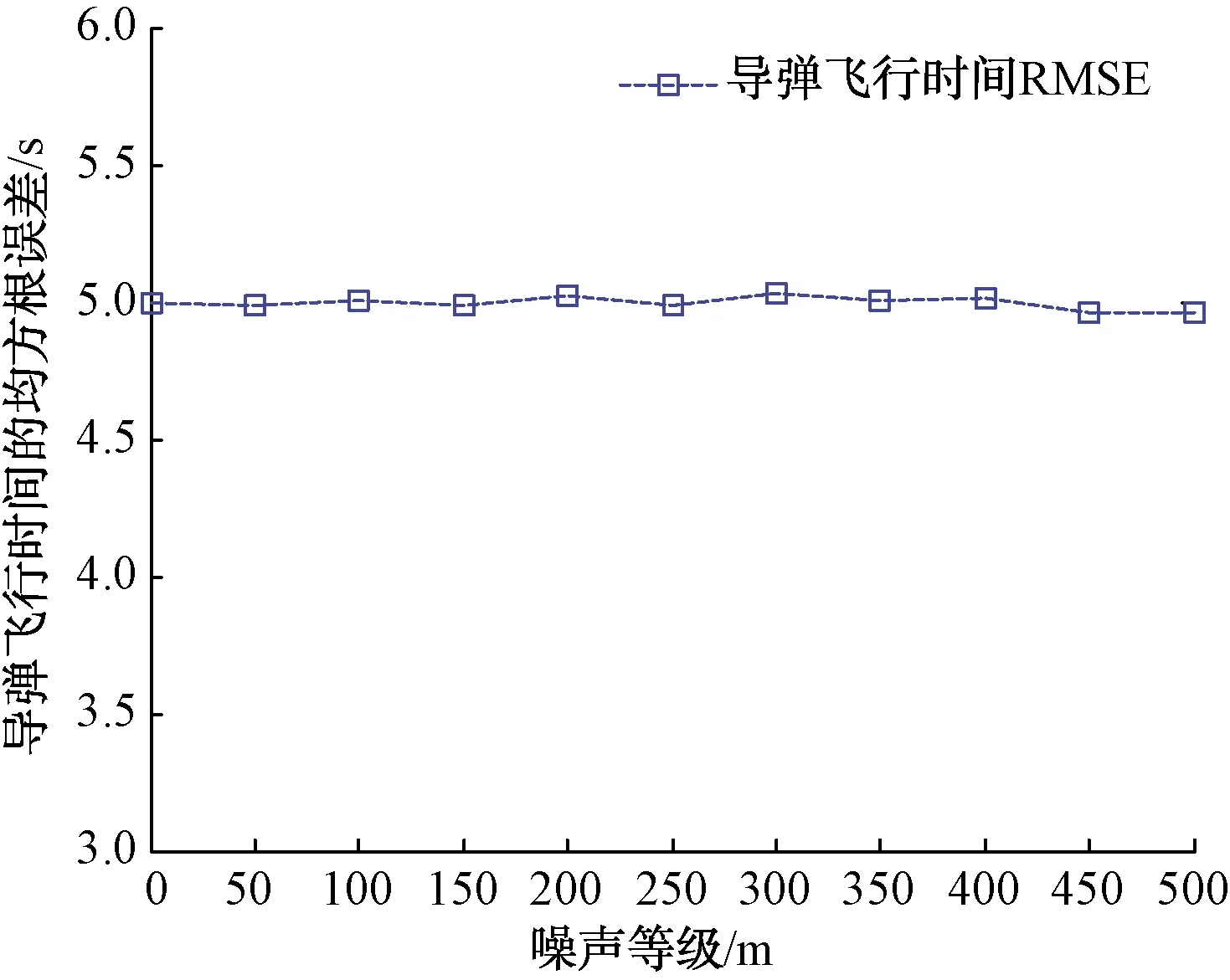
圖7 加入速度測量誤差后的導彈飛行時間RMSE

2.2.3 對導彈的速度測量數據加入誤差，驗證算法

在導彈的速度測量信息中引入均值為0、方差為0∶50∶500的高斯白噪聲，同樣進行100次獨立重復試驗，計算出每次試驗對應的落點預報平均值和均方根誤差，并畫出對應曲線，結果如圖8所示。

圖8 軟件進行導彈飛行時間預測的效果圖

通過圖9可以看出，加入均值u=0、方差為σ=0∶50∶500 m/s的速度測量誤差后，導彈預測飛行的均值穩定在1 810 s附近，有小范圍的變化。即使速度測量誤差的均值u=0，但導彈預測落點均值曲線不是一條直線，而是一條曲線，這說明導彈速度測量誤差對于飛行時間的預測有一定影響。

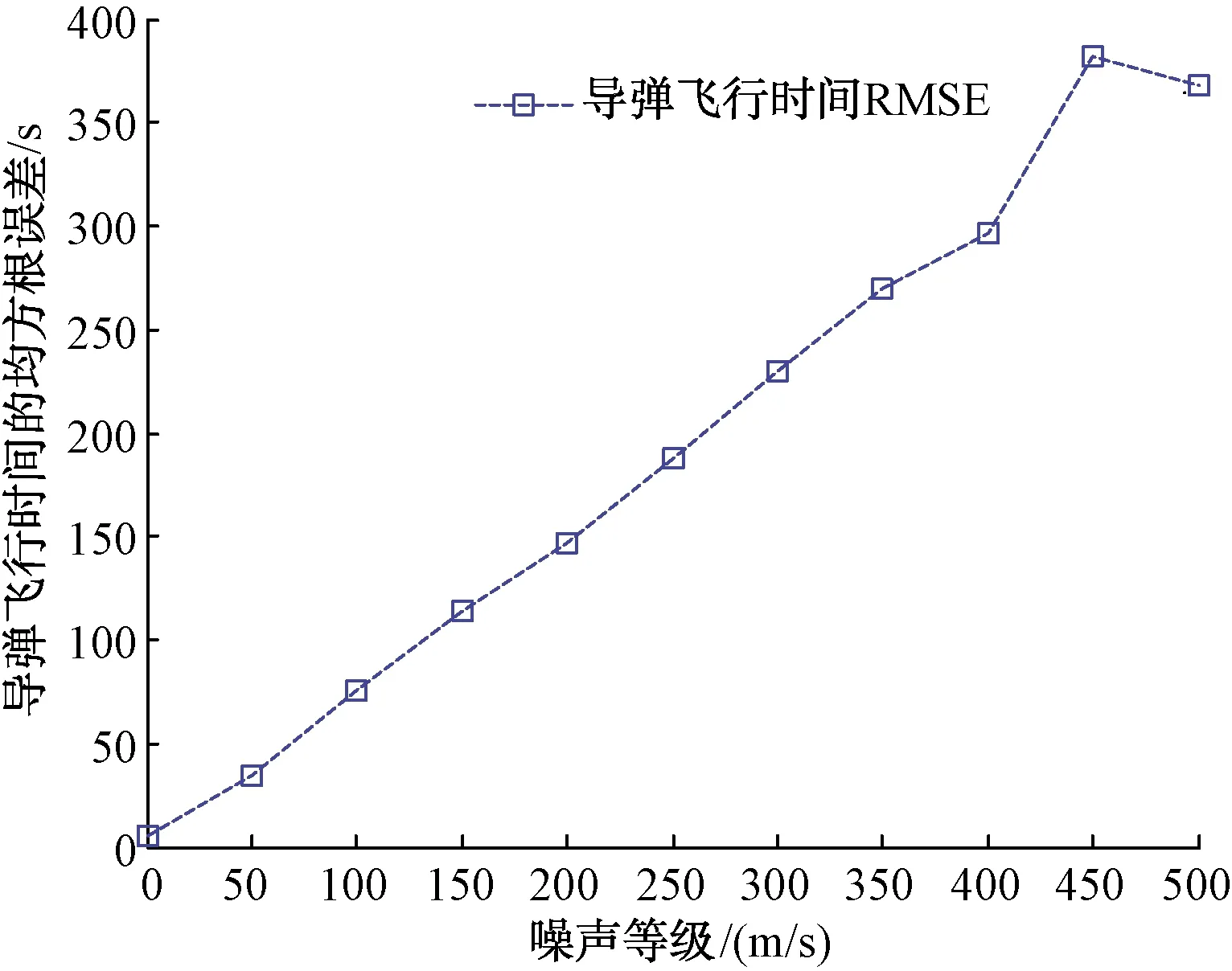
圖9 加入速度誤差后的導彈飛行時間均值

通過圖10可以看出，導彈預測飛行時間的RMSE隨著測量誤差的增大而增大，并且增速較快。

與圖7相比，僅在速度測量誤差σ=50 m/s時，導彈預測落點的RMSE就已達到34.096 6 s；而當測量誤差σ=500 m/s時，導彈預測落點的RMSE將達到347.204 4 s。這說明導彈速度測量誤差對最終的導彈飛行時間預報精度影響較大，在實際應用中，應盡可能地控制速度測量誤差，使其位于較小的范圍內。

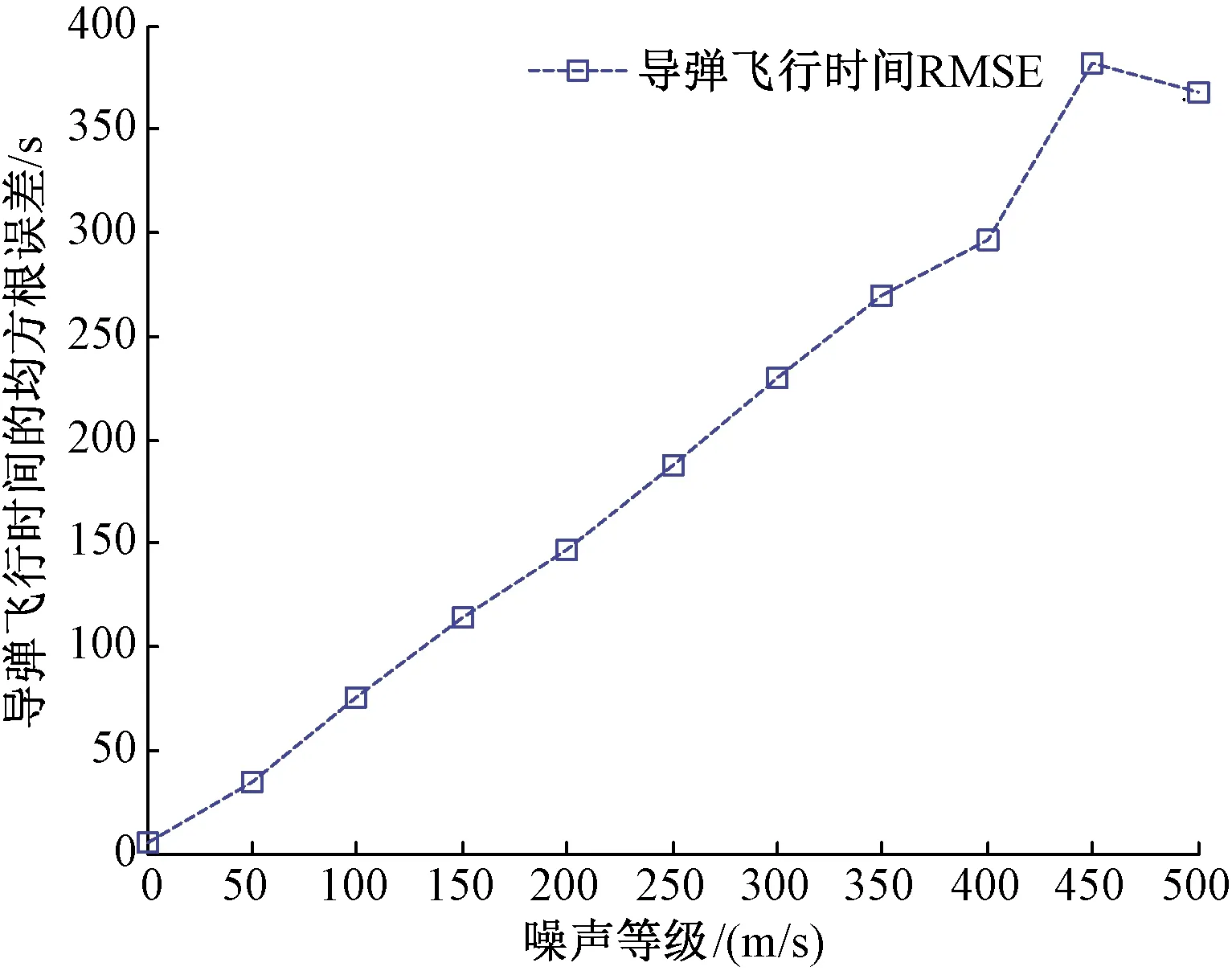
圖10 加入速度誤差后的導彈飛行時間RMSE

2.3 落點預報算法穩定性仿真分析

2.3.1 仿真分析流程

導彈落點預報算法的仿真驗證步驟如圖11所示[7]。

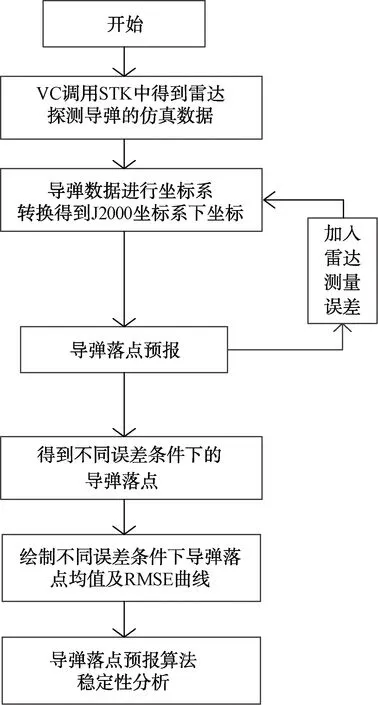
圖11 導彈落點預報算法流程

主要步驟如下：

(1) 利用STK進行雷達探測導彈仿真，得到導彈在飛行過程中每一時刻的位置、速度信息。

通過坐標系轉換，將導彈在極坐標系下的位置信息轉化到J2000坐標系下。

調用向量內積不變算法，進行導彈落點預報。

(2) 在雷達的探測數據中引入測量誤差，并在不同測量誤差等級下進行多次獨立重復試驗，求得各噪聲等級下落點預報均值和均方根誤差。

(3) 繪制曲線圖。

(4) 分析落點預報算法對于測量誤差的穩定性。

2.3.2 對導彈的位置測量數據加入誤差，驗證算法

驗證算法穩定性的步驟為：

首先用VC調用STK建立場景[8-9]，場景的起始時刻為“2007年7月1日12∶00”，結束時刻為“2007年7月2日12∶00”。

隨后建立導彈與雷達坐標系。這里選擇更貼合實際的仿真場景，由于印度始終是我國在西南方向的一個有力對手，其最新研制的“烈火-5”型彈道導彈的打擊范圍已經可以覆蓋北京。

因此假設導彈的發射點位于印度的新德里，其經緯度、海拔為(78.10°，13.37°，0 km)，彈著點假設

位于我國北京，其經緯度、海拔為(116°,39.9°，0 km)。監測雷達位于云南，其經緯度、海拔為(103.34°，34.15°，2 km)。至此場景參數設定完畢。利用雷達監測導彈，得到來襲導彈在不同時刻的位置、速度信息。通過這些數據，調用落點預報算法，就可以進行導彈落點預報。

最后，在雷達所監測到的導彈位置信息中分別引入均值為0、方差為0∶50∶500的高斯白噪聲，進行100次獨立重復試驗，計算出每次試驗對應的預測落點平均值和均方根誤差，并畫出對應曲線，計算結果如圖12～圖14所示。

圖12 加入位置測量誤差后導彈落點預報的效果圖

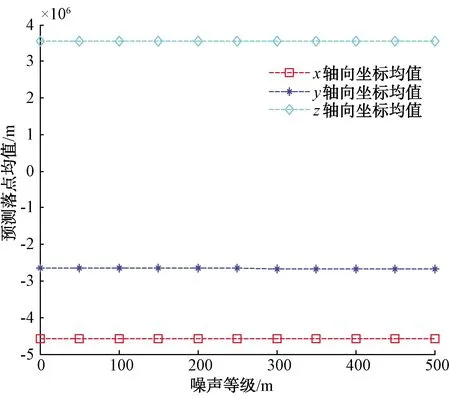
圖13 加入位置測量誤差后的導彈預測落點均值

圖14 加入位置測量誤差后預測導彈預測落點的RMSE

通過圖13可以看出，加入均值u=0、方差為σ=0∶50∶500(單位m)的位置測量誤差后，導彈預測落點的均值比較穩定，變化不大，說明導彈預測落點均值對位置測量的穩定性較好。

通過圖14可以看出，在位置測量誤差σ<150 m時，導彈預測落點的RMSE位于0.043～6.3 km范圍內，比較穩定。并且由正態分布的特性可知，當位置測量誤差σ>150 m時，導彈預測落點的RMSE將隨著測量誤差的增大而驟然增大，說明當測量誤差大于某一等級后，落點預測算法的穩定性開始降低，將無法滿足落點預測精度。因此應該將位置測量誤差σ控制在150 m以內。

2.3.3 對導彈的速度測量數據加入誤差，驗證算法

在得到的導彈在不同時刻的速度信息中引入均值為0、方差為0∶50∶500的高斯白噪聲，同樣進行100次獨立重復試驗，計算出每次試驗對應的落點預報平均值和均方根誤差，并畫出對應曲線，結果如圖15～圖17所示。

圖15 加入速度測量誤差后的導彈落點預報效果示意圖

圖16 加入速度測量誤差后的導彈預測落點均值

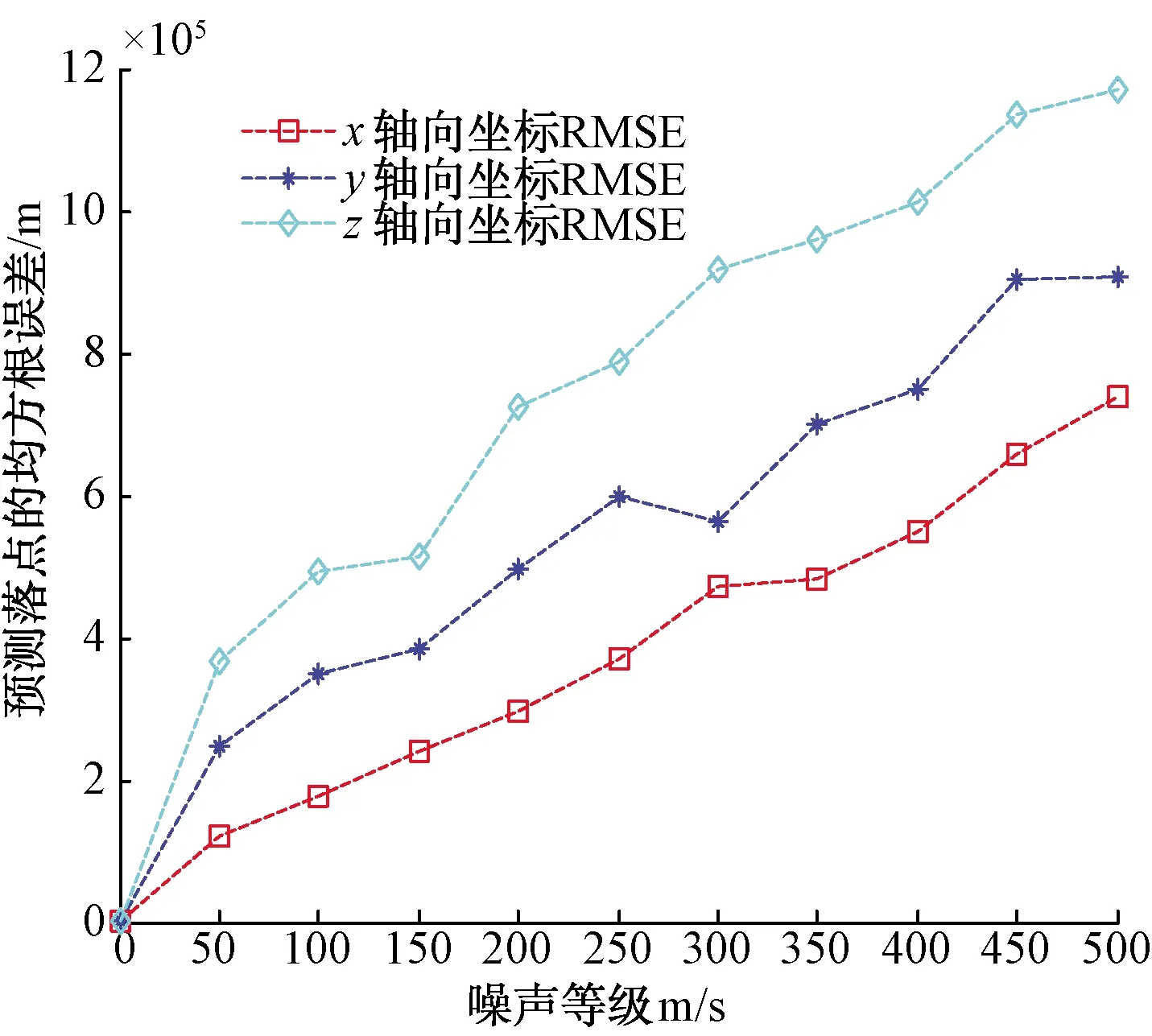
圖17 加入速度測量后的導彈預測落點RMSE

通過圖16可以看出，加入均值u=0、方差為σ=0∶50∶500(單位m/s)的速度測量誤差后，導彈預測落點的均值有小范圍的變化，說明導彈的落點預測與測量速度有一定的關系，即使速度測量誤差的均值u=0，但導彈預測落點均值曲線不是一條直線，而是一條曲線。

通過圖17可以看出，導彈預測落點的RMSE隨著測量誤差的增大而增大，并且增速較快。與圖14相比，僅在速度測量誤差σ=50 m/s時，導彈預測落點的RMSE就已超過10 km，而當測量誤差σ=500 m/s時，導彈預測落點的RMSE將達到126.10 km。說明導彈速度測量誤差對最終的導彈落點預報精度影響較大，在實際應用中，我們應該盡可能地控制速度測量誤差，使其位于一個較小的范圍內。

3 結束語

介紹了導彈的預警參數中的彈著點位置及飛行時間這2個參數的計算模型。對于彈著點進行求解計算，本文采用的是線性空間不變法。這種算法，相較于傳統的解析式法來說，計算量小，運算速度塊，實時性好；在導彈的飛行時間計算方面，本文采用的是橢圓軌道的交點法；在介紹了導彈的預警參數的計算模型之后，本文又對這種算法的穩定性及有效性進行了分析。

通過分析得到了不同類別的測量誤差對導彈預警參數預報精度的影響程度。在計算資源有限的情況下，優先保證對預報精度影響較大的誤差的測量精度，從而能夠對現有的預警過程進行優化，提高導彈預警的準確性。