基于雷達協同的低空目標探測補盲方法

何 青，顧 兵，王曉楠

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225101)

0 引 言

對于艦載雷達而言，其主要作戰目標為低空/超低空飛行的反艦導彈。其飛行高度低、速度快，雷達對此類目標跟蹤時，主波束照射海面。由于海面的鏡像反射，雷達收到的目標回波信號是直接波信號和反射波信號的矢量和。其結果造成目標回波信號強度隨著目標高度和距離而起伏變化，形成雷達盲區，導致雷達在特定距離上無法探測到目標[1]。

1 低空目標探測盲區分析

多路徑效應是由于在雷達探測目標過程中，海面或地面對雷達波的反射影響目標回波信號引起的目標檢測和跟蹤問題。雷達在海洋環境下進行低空、掠海飛行目標探測時，受多路徑影響尤為顯著。多路徑效應與雷達架高、目標高度、目標距離、雷達工作頻率、雷達波束寬度、海面反射系數、雷達電磁波極化等因素均有關系[2]。

為研究多路徑效應，建立多路徑模型時通常用幾何光學方法來避免復雜的電磁場換算。根據實際應用要求的不同，確定采用平面反射模型或者球面反射模型。平面反射模型相對較簡單，近距離目標探測采用平面反射模型是比較準確的。球面反射模型比較復雜，計算量較大但模型精度高[3]。

2種反射模型分析如圖1和圖2所示。

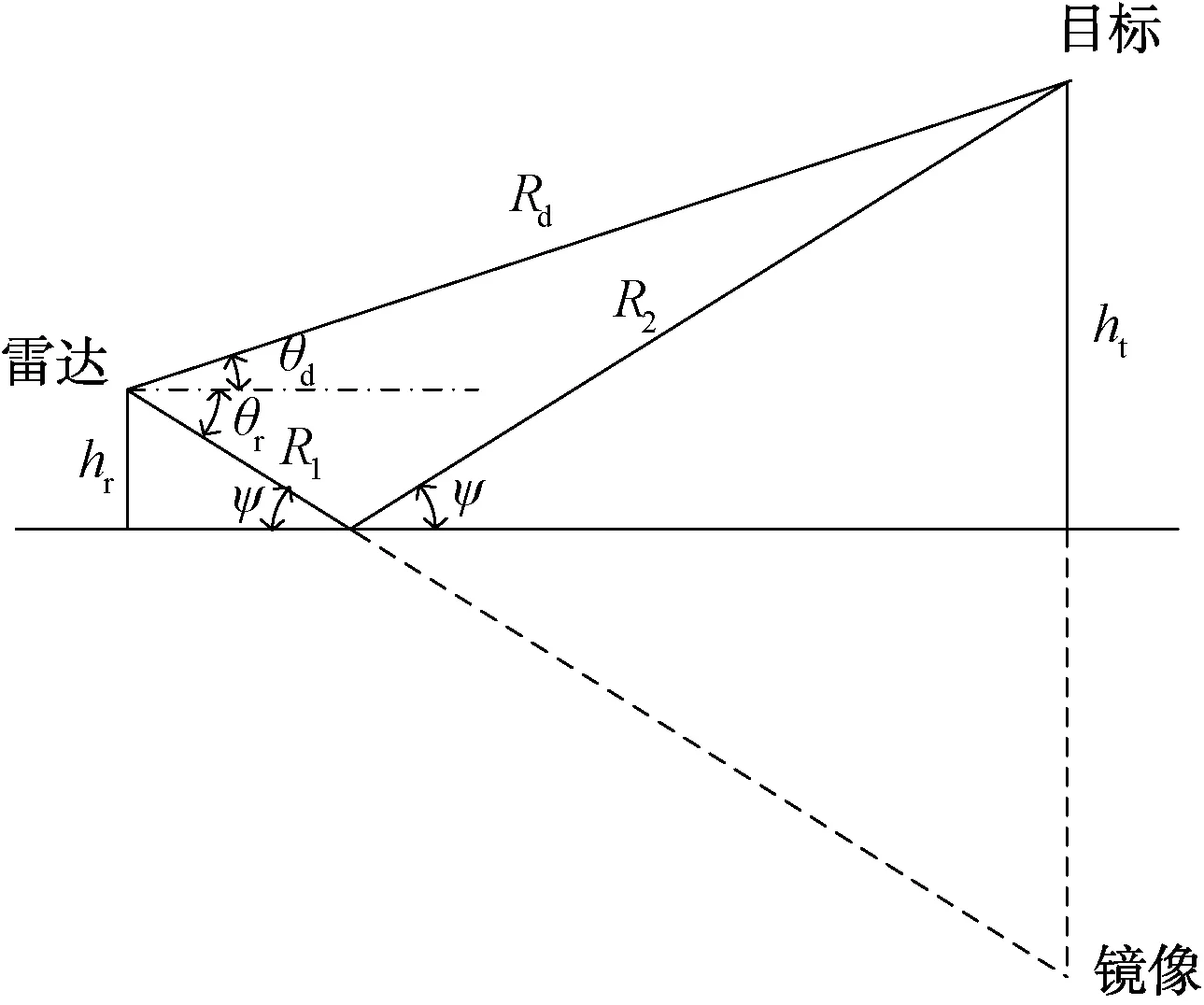
圖1 多路徑平面反射模型圖

圖2 多路徑球面反射模型圖

圖中hr為天線高度，ht為目標高度，Rd為直射路徑，R1和R2為反射路徑，θd為直接路徑的仰角，θr為反射路徑仰角，ψ為入射余角。

平面反射模型中直接路徑與反射路徑的波程差為：

(1)

當雷達距離目標較遠時，雷達的水平面與目標反射點的水平面相差角度較大，仍然采用平面反射模型會產生較大誤差。球面反射中，要計算直接路徑與反射路徑之間的波程差，需要先用中間變量法解方程，計算反射點位置，再通過幾何關系來計算得出直接路徑與反射路徑之間的波程差。球面反射模型中直接路徑與反射路徑的波程差為：

(2)

多路徑條件下，對于直接信號而言，如果差信號Δd與和信號Σd同相，則多路徑反射信號中的差信號Δi與和信號Σi反相，合成矢量關系如圖3所示[2]。

圖3 多路徑條件下和差信號矢量合成圖

合成后的和信號為：

Σ=VΣ(θd)+ρVΣ(θr)

(3)

考慮鏡面多路徑效應，目標仰角θd與鏡像仰角θr大小相同，則式(3)可變為：

Σ=VΣ(θd)+ρVΣ(-θd)=VΣ(θd)·(1+ρ)

(4)

式中：VΣ為和路接收電壓；ρ=|ρ|ejφ，為復反射系數，φ為反射系數的相角。

復反射系數ρ與雷達極化方式、工作頻率、擦地角ψ和表面介電常數等因素有關，在理想鏡面反射條件下，當擦地角ψ很小時，信號的總相移接近180°，ρ=-1，直接信號與反射信號相互對消，和路信號為零，即和通道無輸出，雷達無法檢測到目標。

若目標的雷達截面(RCS)對直接路徑和反射路徑均相同，多路徑下的雷達方程可表示為：

Rmax=Rmax0[1+ρ2g2+2|ρ|g.

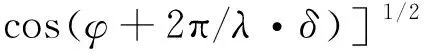
(5)

式中:Rmax為多路徑下的雷達最大作用距離;Rmax0為雷達在自由空間的最大作用距離;g為目標天線增益和鏡像天線增益的比;δ為直接路徑與反射路徑的波程差(見公式(1)、(2))。

由公式(5)可以看出，多路徑下的雷達最大作用距離隨著波程差δ呈現周期性的變化，導致雷達在多路徑條件下存在探測盲區。

2 雷達協同低空目標探測補盲方法

雷達低空探測盲區由多路徑效應引起，盲區的周期與雷達頻率、雷達架高、目標高度和目標距離等因素相關。傳統雷達通常采用頻率分集或者頻率捷變的方法來補盲，其原理為采用不同頻率的雷達信號進行低空目標探測時，直接路徑與反射路徑合成的回波相位差不同，從而導致回波信號盲區位置發生變化，綜合各頻率回波信號，達到回波信號去相關效果，實現低空目標探測補盲的目的[4]。

利用平面多路徑模型中直接路徑與反射路徑的波程差，可以得出其相位差Δφ為:

(6)

隨著目標距離Rd的變化，相位差Δφ發生周期性的變化，并且變化的周期是不固定的。頻率分集或者頻率捷變利用改變雷達工作頻率f的方法改變直接路徑與反射路徑的相位差Δφ，要達到回波去相關效果，需要雷達具備相當大的工作帶寬，通常要求在9 GHz左右。在實際應用中，超寬帶雷達受器件的水平、零漂、成本等諸多因素限制，頻率分集雷達則大大提高了系統復雜程度和成本。

通過公式(6)可知，直接路徑與反射路徑的相位差Δφ還與天線高度hr、目標高度ht、目標距離Rd相關。目標高度為不可控因素，通過雷達協同方法可以實現天線高度、目標距離的變化，即將不同位置的2部或多部雷達進行協同處理、控制，實現直接回波與反射回波去相關，進行雷達協同低空目標探測補盲。

2.1 不同天線高度的雷達協同低空目標探測補盲方法

2部高度不同的雷達同時執行低空目標探測任務，利用雷達天線高度不同產生的目標多路徑相位差進行雷達協同，實現探測補盲。根據去相關理論，將公式(6)變換得出雷達所需架高差為：

(7)

設定目標高度20 m，2部雷達的工作頻率為10 GHz，目標距離為6 km，通過上式可計算出2部雷達所需的架高差為4.5 m。在實際工程應用中較容易實現，特別適用于同平臺雷達協同目標探測任務。

2.2 不同目標距離的雷達協同低空目標探測補盲方法

2部與目標距離不同的雷達，同時進行低空目標探測任務，利用雷達與目標距離的不同產生的目標多路徑相位差進行雷達協同，實現探測補盲。根據去相關理論，將公式(6)變換得出雷達所需架設距離差為：

(8)

設定目標高度20 m，2部雷達的架高為15 m，2部雷達工作頻率為10 GHz，通過上式可計算出2部雷達所需的架設距離差為20 km，實際工程應用中較難實現。

綜上分析，通過架設高度不同的2部雷達，進行協同低空目標探測任務，理論上可以比較容易實現目標的探測補盲。

3 仿真分析

仿真設定參數如下：目標RCS為0.1 m2，高度20 m，A雷達工作頻率10 GHz，架高為15 m，發射功率1 kW，天線增益36 dB，噪聲系數6 dB，改善因子33 dB；B雷達工作頻率10 GHz，架高為19 m，發射功率1 kW，天線增益36 dB，噪聲系數6 dB，改善因子33 dB。

在不考慮多路徑盲區影響的情況下，雷達威力仿真如圖4所示，雷達最大作用距離為13.7 km。

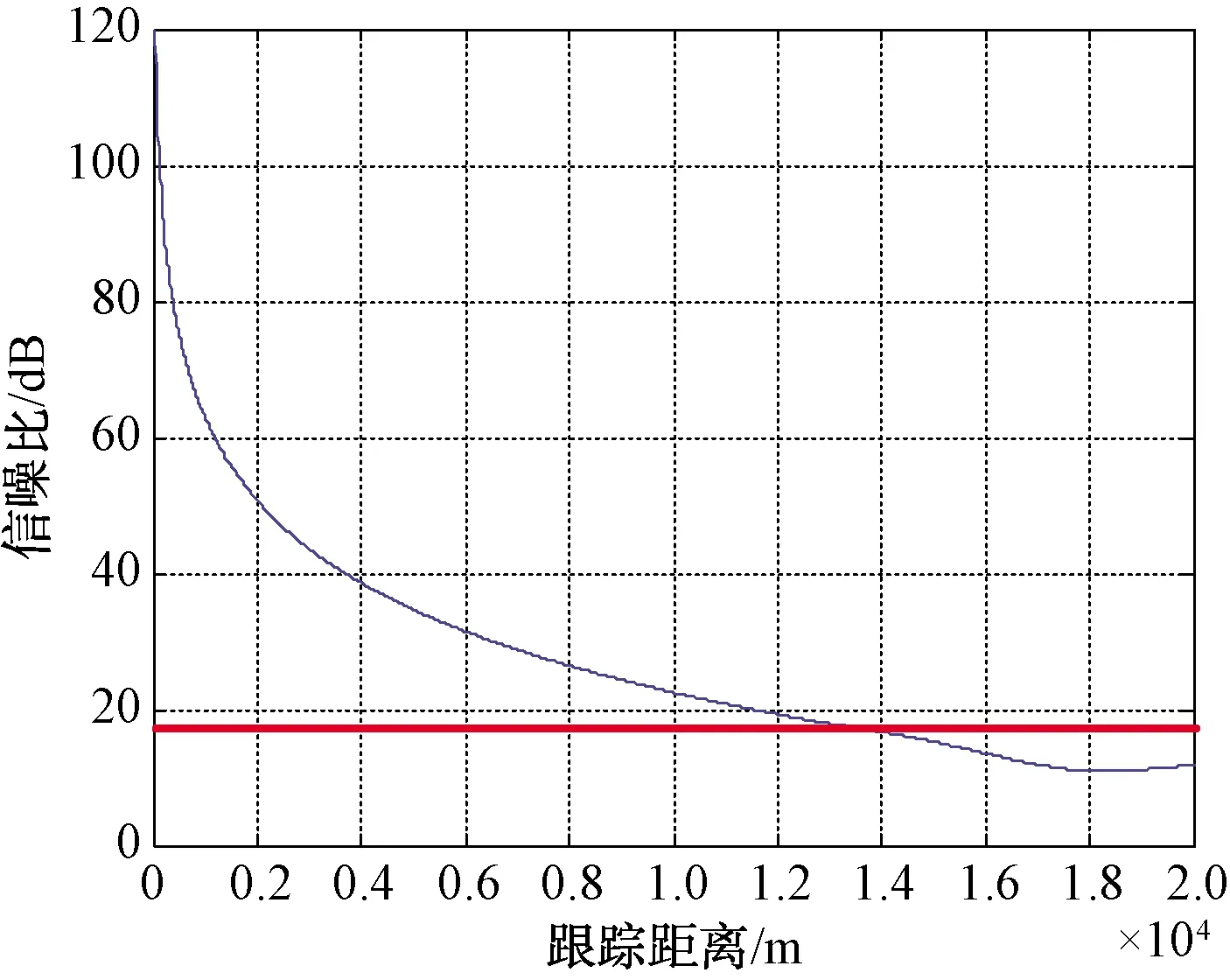
圖4 雷達威力仿真結果(無多徑影響)

設定3級海情，A雷達威力仿真結果如圖5所示。雷達在10 km內的約4.8 km、6.2 km、8.7 km 3處出現探測盲區，此時接收回波信噪比小于雷達最小可檢測信噪比，雷達無法發現目標。

圖5 A雷達威力仿真結果

設定3級海情，B雷達威力仿真結果如圖6所示。雷達在10 km內的約4.6 km、5.7 km、7.3 km 3處出現探測盲區，此時接收回波信噪比小于雷達最小可檢測信噪比，雷達無法發現目標。

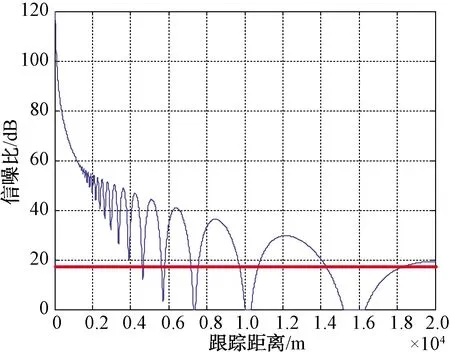
圖6 B雷達威力仿真結果

A雷達與B雷達協同后威力仿真結果如圖7所示。雷達協同后在10 km內接收回波信噪比均大于雷達最小可檢測信噪比，無探測盲區。仿真中雷達架高相差4 m，符合艦載平臺雷達的實際情況。

通過以上仿真結果可以看出，利用不同架高的雷達協同進行低空目標探測，可以達到目標探測補盲的效果。

4 結束語

低空目標的探測盲區一直是雷達目標探測的難題，本文基于雷達架高對接收回波的影響，提出了一種基于雷達協同的低空目標探測補盲方法，并仿真分析了利用該方法進行低空目標探測補盲的有效性，證明該方法具有較好的工程應用價值。

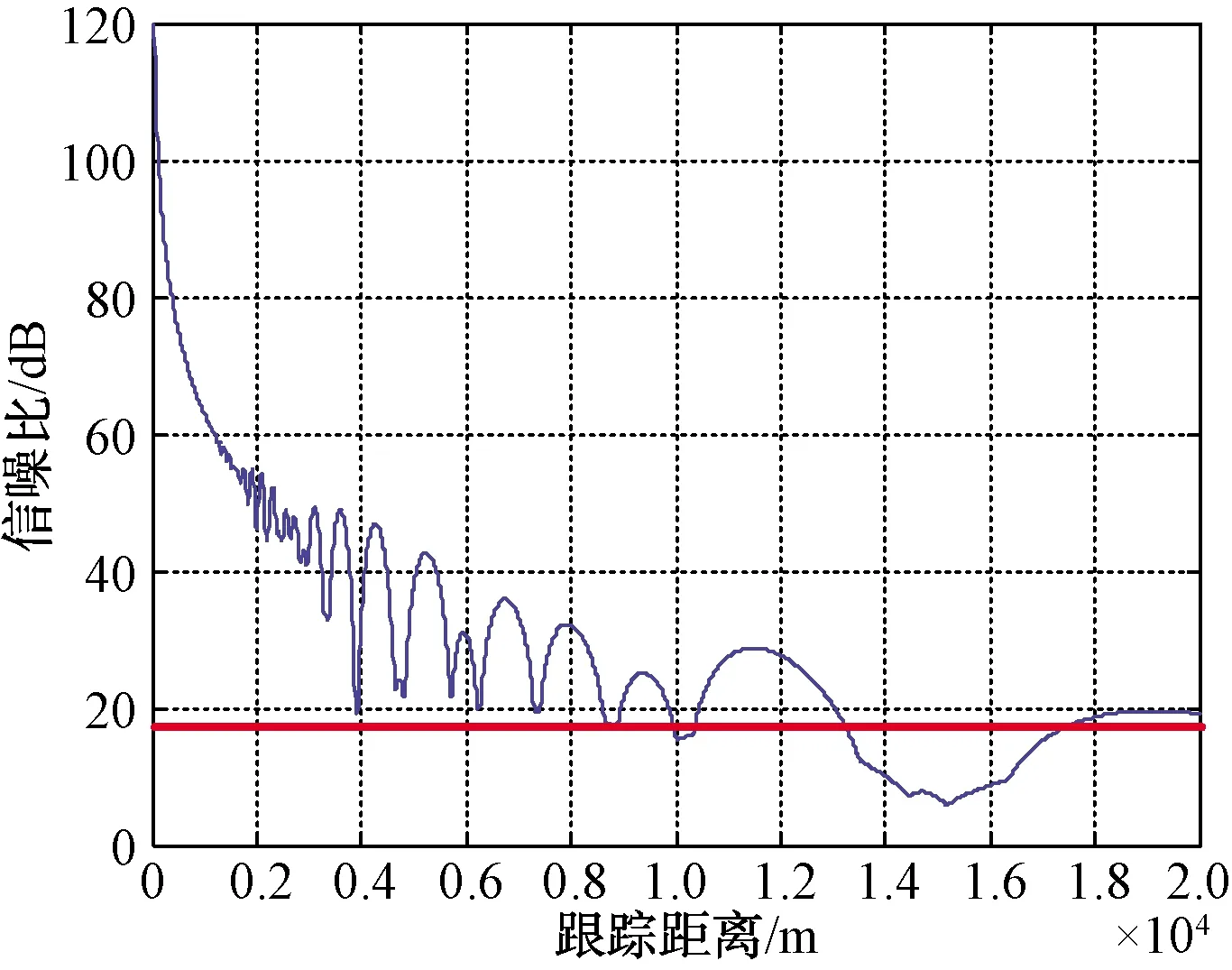
圖7 雷達協同后仰角測量誤差仿真結果