城市峽谷中基于GPS 雙極化天線的定位方法

王冠宇，孫 蕊，程 琦

（南京航空航天大學 民航學院，南京 211106）

0 引言

全球衛星導航系統（global navigation satellite system, GNSS），尤其是全球定位系統（global positioning system, GPS），在定位和授時方面得到了廣泛的應用，對科學研究、經濟建設和改善民生的諸多領域產生了深刻的影響[1]。然而，由于信號會被建筑物所阻擋或反射，GPS 在建筑密集的城市地區的定位精度不夠可靠。GPS 信號接收類型分為視距信號（line-of-sight, LOS）、非視距接收信號（non-line-of-sight, NLOS）和多徑干擾信號（multipath, MP）3 種。其中：LOS 指的是從衛星直接到達接收機的信號；NLOS 指經反射到達接收機的信號，且接收機沒有收到視距信號；MP 指接收機同時接收到LOS 和NLOS 信號。NLOS 和 MP都會降低GPS 的定位精度，且造成的誤差不能通過差分定位消除[2]，后文將這 2 種信號統稱為MP/NLOS 信號。此外，NLOS 可能造成 100 m 左右的定位誤差[3]。為此，國內外學者提出了多種方法來減少MP/NLOS 對導航定位的影響。

使用扼流圈天線[4]可以有效地減輕低高度角情況下的多徑效應，但價格昂貴且笨重，目前主要用到大地測量領域。文獻[5]改善相關器設計，縮小早遲相關器的間隔來減小多徑誤差；此后又出現了頻閃相關器[6]和視覺器相關器[7]等。這些方法能在一定程度上降低 MP 造成的誤差，但是對于NLOS 并不有效。

將衛星的觀測值與其數據源結合，可有效減輕MP/NLOS 信號對定位精度的影響。GPS 與慣性導航系統（inertial navigation system, INS）的結合可以使2 種系統取長補短，從而彌補MP/NLOS 信號導致的精度下降[8]，但定位結果高度依賴INS 性能。GNSS與視覺傳感器的結合也可降低多徑誤差，提高定位精度[9]，但易受天氣等因素影響。依賴額外傳感器，無疑會造成價格的提升。將3 維（3D）城市模型作為信息源，可以以較低的成本降低多徑誤差。使用3D 城市模型，可以檢測進而排除掉 NLOS 的信號[10]，然而會導致可用衛星數減少。文獻[11]提出了陰影匹配方法，先根據3D 城市模型預測信號接收類型，再與實際信號的接收類型進行比較，匹配程度最高的位置最可能是真實位置。文獻[12]使用3D城市模型模擬信號傳播路徑從而計算模擬偽距值，再和偽距觀測值比較，通過相似度來為候選點定權，從而采用加權平均的方法獲得定位解。這些方法依賴對3D 城市模型的及時更新，對3D 模型的精度要求較高。此外對信號接收類型的準確判斷也是此類方法的關鍵。只有準確地區分信號接收類型，才能得到較高的定位精度。

傳統的信號接收類型區分方法是對載噪比（carrier to noise ratio, C/N0）劃定閾值，C/N0較高的信號被分類成 LOS，C/N0較低的信號則被分類成 NLOS。文獻[13]證明了在沒有干擾的條件下，靠 C/N0值能得到可靠的分類結果，然而在實際情況下，由于天線位置變化、瞬間阻擋等原因，可能會出現LOS 信號表現為低C/N0值，而NLOS 信號表現為高 C/N0值的情況[13]。這種情況難以避免，因此僅依賴 C/N0是不夠的，還需要引入更多的特征。衛星高度角也可作為分類指標之一。一般來說，高度角越低，信號是NLOS 的可能性越大；高度角越高，衛星被建筑擋住的可能就越小。文獻[14]提出基于衛星高度角和幾何精度因子的選星算法，分析了高度角對定位精度的影響。文獻[15]在智能手機陰影匹配算法的研究中，也將 C/N0和衛星高度角結合分析，以判斷LOS 的可能性。此外，越大的偽距殘差意味著 NLOS/MP 的概率更大，因此對偽距殘差進行一致性檢驗，也可檢測MP/NLOS 信號[16-17]。使用雙極化天線也可檢測NLOS/MP 信號，GNSS 的直射信號表現為右旋圓極化（right-hand circularly polarized, RHCP），在建筑物反射后，入射角小于布魯斯特角的信號變為左旋圓極化（left-hand circularly polarized, LHCP），其余保持RHCP[18]。雙極化天線在1 個外殼中，將同軸 RHCP 敏感天線和 LHCP 敏感天線結合在一起，具有2 個輸出：1 個是對RHCP 信號更敏感的常規輸出，另1 個是對LHCP 信號更敏感的附加輸出。經過反射后，總的接收信號將同時具有 LHCP 和RHCP 分量。受多徑效應影響更嚴重的信號則具有更強的LHCP 分量。利用這個原理，文獻[18]通過比較左、右旋圓極化天線輸出的C/N0來檢測NLOS信號[19]，若LHCP 天線的C/N0較大，則將該信號判斷為NLOS。但由于天線的極化靈敏度隨入射角的變化而變化，該方法在高度角較大的情況下效果較好，而對于低高度角信號效果較差[20]。因此僅憑 LHCP 和 RHCP 的 C/N0差值檢測 NLOS 是不可取的，但LHCP 的C/N0可以作為分類特征。

機器學習可高速準確地處理多種類型特征，近年已被應用于提高 GNSS 定位精度。文獻[21]將高度角和方位角作為支持向量機（support vector machine, SVM）的關鍵特征，以減輕靜態定位的多徑效應。文獻[13]將C/N0、高度角等作為特征，用決策樹區分 LOS 和 NLOS[13]。文獻[22]提出了在車輛協作環境下，使用機器學習檢測 NLOS 信號的方法。這些研究證明了機器學習是進行GPS 信號接收類型區分，提高定位精度的1 種有效工具。

MP/NLOS 信號會降低定位精度，因為2 者都會對偽距造成誤差。通過修正偽距誤差，或在定位過程中剔除受到影響的信號，都能夠有效地提高定位精度。因此，針對上述方法的不足，本文提出基于雙極化天線和梯度提升決策樹（gradient boosting decision tree, GBDT）的GPS 信號接收類型分類方法和基于分類結果的定位方法。根據接收機的真實位置，計算每個衛星的偽距誤差，并以RHCP 和LHCP 的信號強度、偽距殘差、衛星高度角等測量值為特征，使用 GBDT 擬合偽距誤差。然后利用 GBDT 預測的偽距誤差的絕對值與閾值進行比較來對信號接收類型進行分類。此后對判斷出的 MP/ NLOS 信號進行剔除或修正，用以提高定位精度。該方法不依賴INS 等昂貴的傳感器，也不需要3D 城市模型，因而應能以較低的成本提高定位精度。

1 基于雙極化天線和GBDT 的信號接收類型分類和定位方法

基于雙極化天線和GBDT 的偽距修正和信號接收類型分類方法流程如圖1 所示。

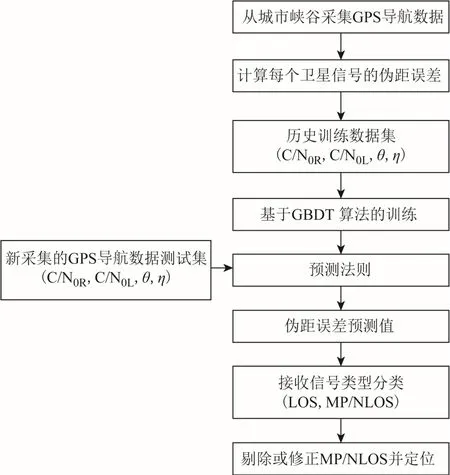
圖1 算法流程

首先在已知位置使用雙極化天線采集信號。對于每個衛星信號，分別采集其在RHCP 天線輸出的載噪比和LHCP天線端輸出的載噪比，與偽距殘差η、衛星高度角θ數據組成歷史訓練數據集。根據真實位置計算每個信號的偽距誤差，并用GBDT 算法進行擬合。此后可對測試集的偽距誤差進行預測，將GBDT 預測的偽距誤差的絕對值與閾值相比較，以對GPS 信號接收類型進行分類，此后將判斷出的 MP/NLOS 信號進行剔除或修正，以進行更精確的定位。

1.1 偽距誤差計算

衛星信號經反射到達接收機過程中，會經過額外的路程，導致NLOS 信號偽距增大，引起正的偽距誤差。而 MP 信號是直射信號與反射信號的疊加，經相關器處理后，會出現正或負的偽距誤差。2 者降低定位精度的原因都是偽距誤差，因此本文將2 者歸為一類，稱為MP/NLOS 信號。接收機到某衛星之間的偽距ρ為：

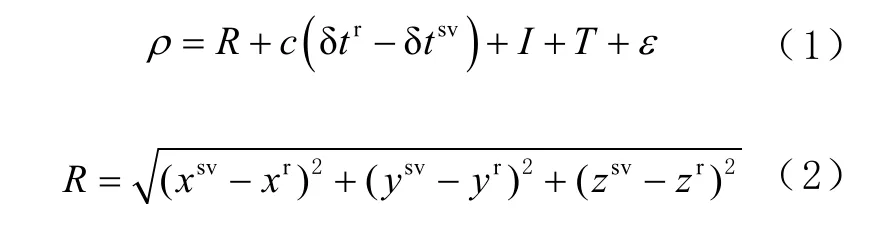
式中：R為衛星與接收機之間的幾何距離分別為衛星和接收機在地心地固坐標系（Earth centered Earth fixed, ECEF）中的坐標；c為光速；分別為衛星和接收機的鐘差；I和T分別為電離層和對流層的延遲；ε為包含了MP/NLOS、接收機噪聲等造成的誤差。這里考慮到噪聲相對較小，可忽略不計，主要誤差為MP/NLOS誤差。衛星位置和衛星鐘差修正值可由星歷獲得。已知接收機位置可計算衛星與接收機間幾何距離，接收機鐘差修正值也可通過解算偽距方程組獲得。IK為Klobuchar 模型獲得的電離，TS為Saastamoinen 模型獲得的對流層延遲。因此，經過修正后的偽距ρc為：

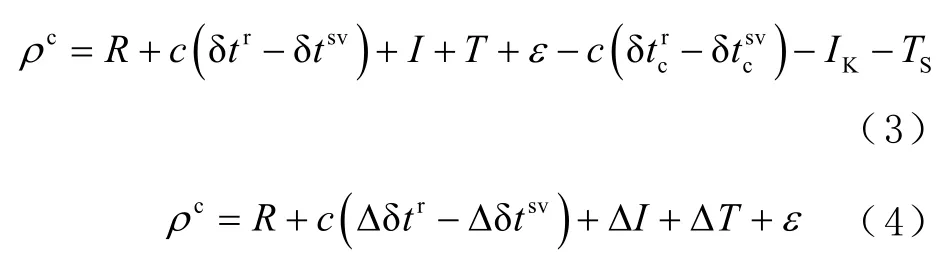
偽距誤差Δρ的計算式為

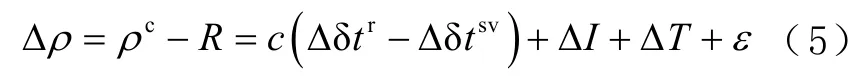
1.2 特征選取

在選擇機器學習中輸入的特征時，應同時考慮準確性和計算效率。盡管使用更多特征能在一定程度上提高準確性，但會降低計算效率。因此，僅使用以下4 個特征：

3）偽距殘差η。偽距殘差對信號接收類型分類具有很大的價值[23]。理論上，偽距殘差的絕對值大小與 NLOS 的概率成正比，更大的偽距殘差意味著NLOS 的概率更大；當采集的數據中，小部分信號是 NLOS 時，這種情況更突出[24]。文獻[17]已證明，若有足夠多的測量值，偽距殘差可以作為1 個特征來檢測MP 和NLOS 信號。

4）衛星高度角θ。一般來說，從高度角更高的衛星上發射出的信號更不容易被建筑遮擋，被建筑反射的可能更小，直線抵達接收機的可能性更大，越可能是LOS 信號。因此高度角可用作參考特征來減少多徑效應對定位精度的影響。

1.3 基于GBDT 的偽距誤差擬合

GBDT 是 1 種監督式機器學習算法[25], 它使用梯度提升思想將多個決策樹結合起來。歷史訓練數據集中的每個樣本表示為其中，為樣本序號，N為樣本數量。歷史訓練數據集可表示為T=其 中Δρi為每個樣本的偽距誤差。GBDT 每次迭代都沿著負梯度方向創建1 個弱學習器來減小損失函數的期望，其中a是決策樹的參數，包括每個節點的分裂特征、最佳分割點、節點的預測值。本文中使用的損失函數為

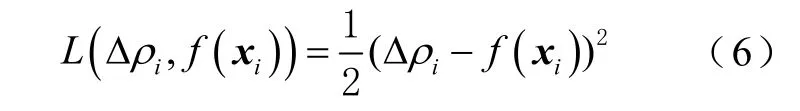
設迭代次數為M，算法流程如下:

1）初始化弱學習器 f0（x）為

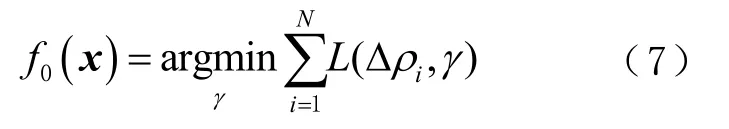
式中：f0（x）為僅含1 個根節點的決策樹；γ為其輸出。由于L為平方損失函數，f0（x） 為

① 計算負梯度為

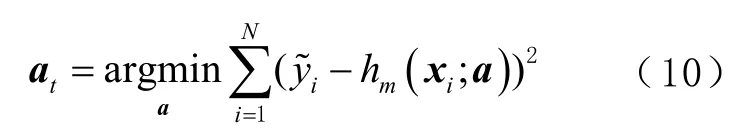
③更新強學習器為

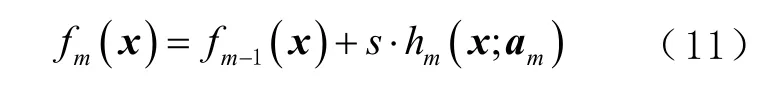
式中s是學習率，為防止過擬合，通常選在0～1 之間。

3）迭代結束后，輸出fM（x）為最終的強學習器為

fM（x） 可以用來預測新樣本的偽距誤差。

1.4 定位方法

考慮到預測的偽距誤差包括鐘差、電離層和對流層延遲的殘差項，即使LOS 信號也具有較小的偽距誤差；因此設置閾值p以避免此類殘差影響分類。偽距誤差預測值的絕對值小于閾值的信號被分類為 LOS，反之則被分類為 MP/ NLOS。將MP/ NLOS 信號剔除后，可以提高定位精度。但由于剔除衛星信號會使衛星幾何分布變差，可能會造成定位精度不提高反而變差的情況，因此設計了基于MP/NLOS 剔除與修正的定位方法，流程如圖2 所示。該方法不會剔除所有 MP/NLOS 信號。對于每個MP/NLOS 信號，先判斷將其剔除后對位置精度衰減因子（position dilution of precision,PDOP）的影響。若將其剔除不會導致PDOP 值增大，則會將其剔除；若剔除導致PDOP 增加，不剔除此信號，而是對其進行修正，即將該信號的偽距測量值減去偽距誤差預測值。

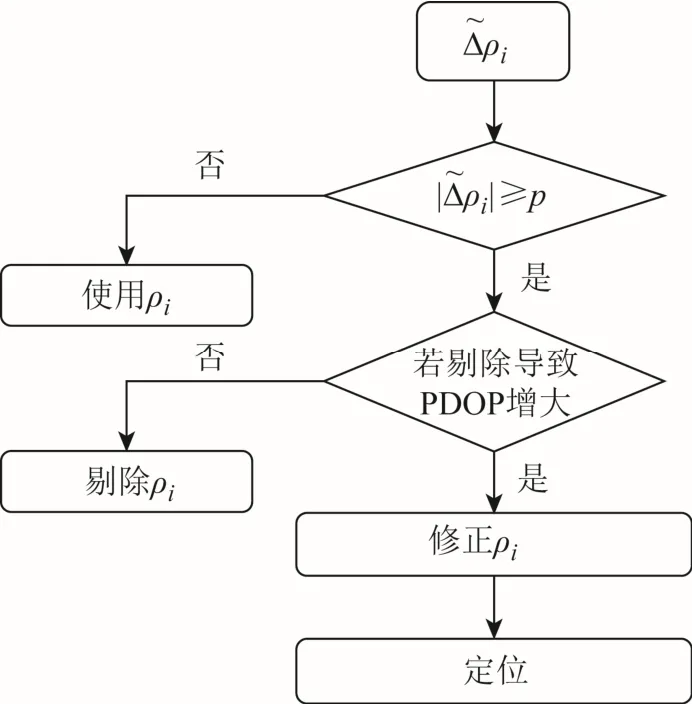
圖2 基于MP/NLOS 剔除與修正的定位方法

2 實驗與結果分析

為驗證所提出的算法，筆者在中國臺灣成功大學使用加拿大諾瓦泰公司的NovAtel Propak7 GPS接收機，以及浙江中裕通信技術有限公司的ZYACF-L004 型號的雙極化天線，采集近7 h 的數據，計算每個信號的偽距誤差。實驗場景及所用雙極化天線如圖3 所示。

圖3 實驗場景及所用雙極化天線

考慮到偽距誤差包含式（5）中的各殘差項，將閾值設為5 m，若數據集中偽距誤差絕對值大于閾值，則分類為MP/NLOS 信號，反之則分類為LOS信號。抽取2 種樣本各10 000 個生成訓練集，將全部數據作為測試集和訓練集，數據集樣本數量如表1 所示。

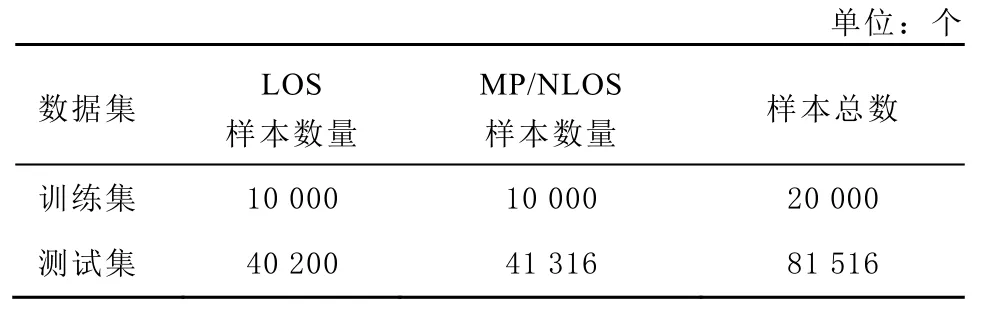
表1 各數據集樣本數量

本文使用GBDT 對歷史訓練數據集進行訓練，并使用訓練出的擬合規則對訓練集和測試集的偽距誤差進行預測，以測試算法。使用訓練出的擬合規則對訓練集本身進行的評估稱為驗證，利用測試集對算法進行的評估稱為測試。本文將 GBDT算法與傳統的線性擬合方法和二次多項式擬合方法[26]進行了比較。3 種方法擬合結果的均方根誤差（root mean square error, RMSE）如表2 所示。從表2 可以看出，GBDT 算法的驗證結果和測試結果的RMSE 均小于其他算法，這體現了GBDT 算法擬合偽距誤差的優越性。

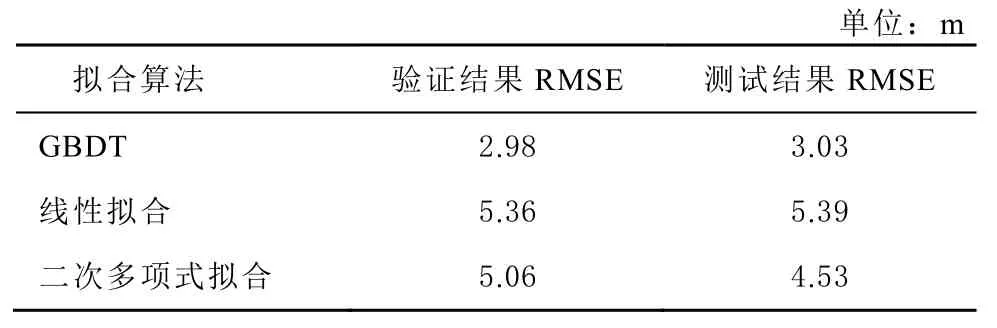
表2 各算法擬合精度比較

GBDT 算法分類準確性如表3 所示。

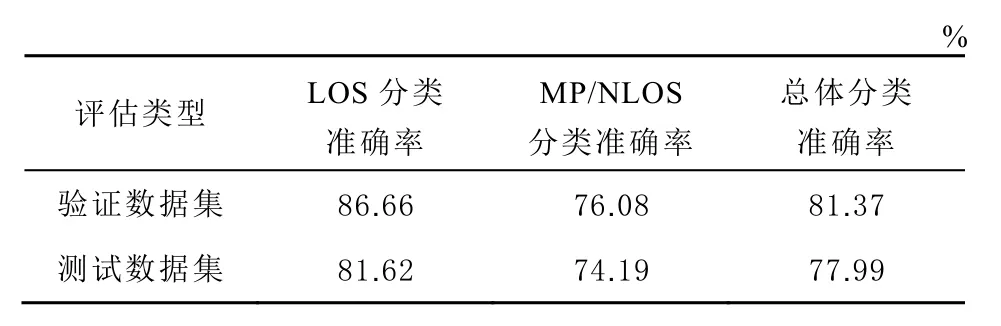
表3 信號接收類型分類準確性

表 3 中分類準確率表示的是正確預測的樣本數量與數據集樣本總數的比值（百分比）。每1 類的準確率指的是被正確分類為這 1 類的樣本數與已知為這1 類的樣本總數的比值（百分比），例如LOS 的分類準確率為，正確分類為LOS 的樣本數與已知為LOS 的樣本總數的比值（百分比）。驗證和測試的總體分類準確率分別為 81.37 %和77.99 %，證明所提出的基于GBDT 的分類算法能夠有效檢測MP/NLOS 信號。

表4 比較了本文所提出的基于MP/NLOS 剔除與修正的定位方法與傳統最小二乘定位解算的定位精度。

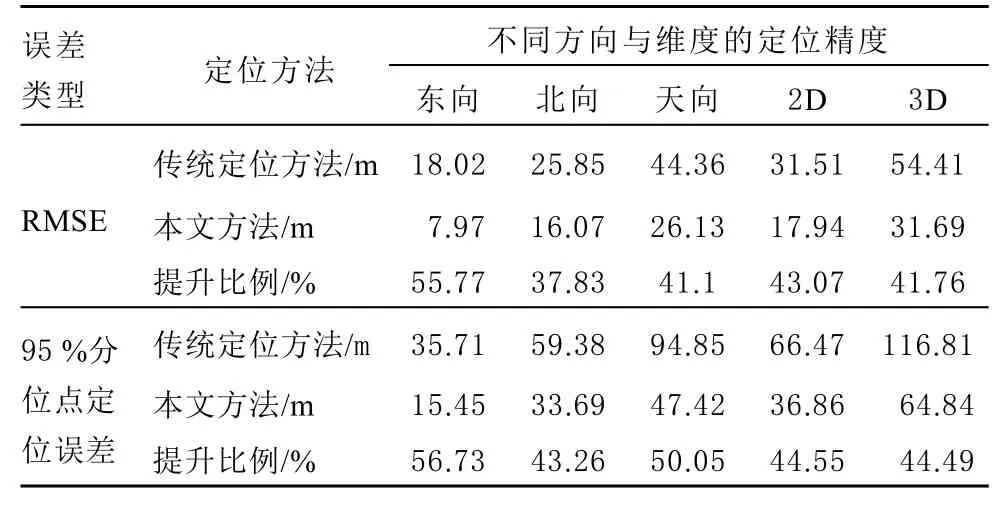
表4 定位精度比較

本文方法在各方向各維度上的定位精度均優于傳統定位方法，其2D 和3D 定位的RMSE 分別為 17.94 和 31.69 m，相比傳統定位方法提高了43.07 %和41.76 %，其2D 和3D 和 95 %分位點定位誤差分別為36.86 和64.84 m，相比傳統定位方法提高44.55 %和44.49 %。2 種方法的定位結果分別如圖4 和圖5 所示。本文提出的方法使得大部分定位解都分布在真實位置周圍，遠離真實位置的定位解數量明顯少于傳統定位方法。綜上所述，所提出的算法能有效提高定位精度。

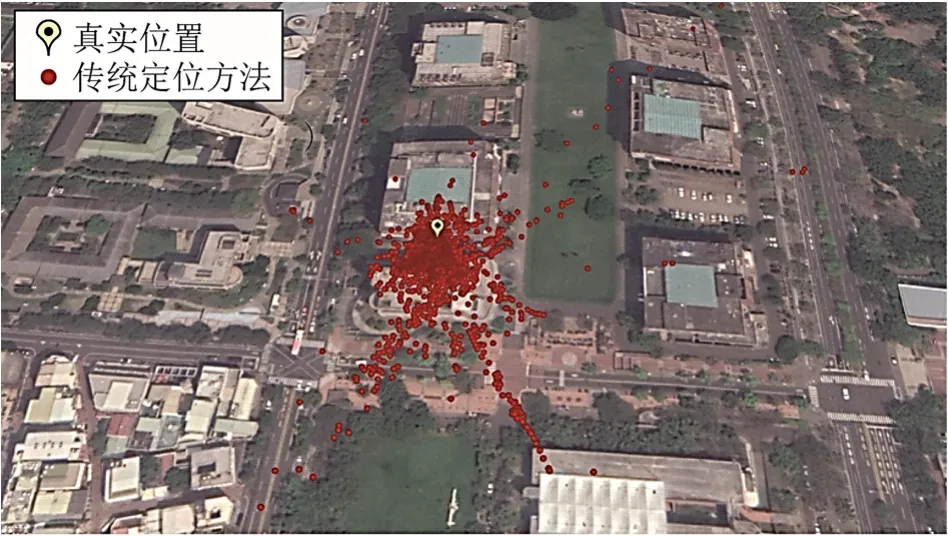
圖4 傳統方法定位結果

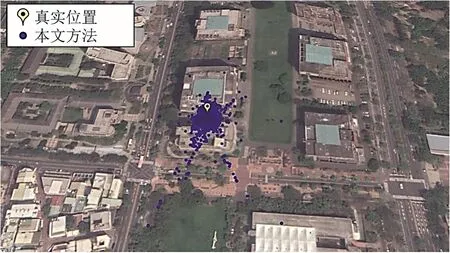
圖5 本文方法定位結果

為了進一步驗證所提出算法，將所提出的方法與傳統定位方法的每個歷元的定位結果進行了比較，如表5 所示。

表5 基于單個歷元的定位精度影響分析

本文提出的方法提高了70 %左右的歷元的定位精度；有14 %的歷元的定位精度沒有發生變化，這是因為在這些歷元時可用衛星只有 4 顆，無法進行剔除或不存在，或未檢測出 MP/NLOS 信號；由于 GBDT 存在誤判，導致有少部分歷元定位精度變差。總體來講，本文所提出的方法對大部分歷元的定位精度有提高效果。

3 結束語

隨著導航定位技術的不斷進步，人們越來越關注城市環境中的高精度定位。本文提出了1 種基于雙極化天線的 GPS 信號接收類型分類算法，并將其判斷出的MP/NLOS 信號進行剔除或修正，以提高城市環境中的定位精度。本文用雙極化天線采集數據，將 RHCP 和 LHCP 天線輸出的載噪比以及衛星高度角、偽距殘差作為特征，使用GBDT 算法對偽距誤差進行擬合。訓練出的擬合規則可用于預測偽距誤差，將其絕對值與閾值進行比較，以對 GPS 信號接收類型進行分類，此后將判斷出的MP/NLOS 信號進行剔除或修正，以進行更精確的定位。實驗證明，所提出方法能夠提高大部分歷元的定位精度，其2D 和 3D 定位的 RMSE 分別為 17.94 和 31.69 m，相比傳統定位方法提高了43.07 %和41.76 %。此外，本文所提出定位方法的95 %分位點定位誤差相比傳統定位方法也有顯著提高。本文所提出的算法不需要高精度慣導等昂貴的傳感器，也不需要3D 城市模型等額外的信息源，且輸入特征較少，因此能以較低的成本、較高的計算速率來提高城市中的定位精度。由于所用特征較少，在提高計算速率的同時，算法對環境變化較敏感。在未來的研究中會使用更多的特征，并且進行動態的定位實驗。