利用視覺信息輔助GNSS 緊耦合定位方法

王 磊，樹玉泉，付文舉 ，馬愛龍，陳銳志，蔚保國

（1. 衛星導航系統與裝備技術國家重點實驗室，石家莊 050081；2. 武漢大學 測繪遙感信息工程國家重點實驗室，武漢 430079）

0 引言

全球衛星導航系統（global navigation satellite system, GNSS）的脆弱性是其服務性能的短板之一，在復雜地理和電磁環境條件下，GNSS 信號受到遮擋或者電磁干擾，往往無法正常地提供導航定位服務。另一方面，隨著電子戰、導航戰等電子對抗形式的出現，僅依賴衛星導航定位技術獲得位置的可靠性逐漸降低，近年來開展GNSS 干擾和GNSS 欺騙的事件時有發生[1-3]。未來的彈性定位、導航、授時（positioning, navigation and time, PNT）框架就是要集成多源異構的多種導航源實現彈性的、堅韌的導航定位服務[4]。而可信PNT，則要求利用多源融合的方法達到導航定位服務高可用的狀態[5]。為了提升GNSS 在復雜和受限環境下的定位性能，本文提出1 種將攝影測量技術和衛星導航技術進行融合的方法，提升導航定位服務在復雜場景下的可用性。

利用影像進行定位的方法，已廣泛地應用到室內場景的導航定位中，例如機器人定位、視覺即時定位與地圖構建（simultaneous localization and mapping, SLAM）等[6]，在室外也主要用于視覺里程計（visual odometer, VO）等近距離定位場景[7]。受到相機分辨率限制，如果物方目標與相機距離變遠，會導致定位精度顯著下降，因此在室外和大范圍場景下，一般不直接使用視覺信息進行絕對定位[8]。視覺定位手段與GNSS 定位技術的融合方法主要分為松耦合和緊耦合2 種。松耦合的方式是2 種定位手段分別提供定位結果，然后利用因子圖等方法對多源定位結果進行融合[9]。而目前緊耦合的方式又分為2 種[10]：①利用對天的相機實時獲取信號遮擋信息，然后輔助GNSS 拒絕接收到的衍射和繞射信號，降低非視距信號（none line-of-sight, NLOS）帶來的誤差，從而提升GNSS 在城市峽谷等區域的定位精度[11]；②將GNSS 信號與視覺里程計等傳感器融合，利用視覺里程計提供的相對位置變化信息，對GNSS 軌跡進行約束來提升定位精度[12]。本文提出1 種觀測值域的緊耦合定位方法，即利用相片與物方平面之間的相似關系，計算相機到物方特征點的距離，再與GNSS 測距信號聯合定位解算。

1 緊耦合組合定位原理

在遮擋或者復雜環境條件下，單獨使用衛星導航技術不足以直接定位，此時可通過攝影測量的方式增加觀測值，實現協同定位。具體的思路是利用攝影測量的原理，確定用戶終端到相片上若干標志物之間的距離，再聯合衛星測距和攝影測量測距的方式求解用戶終端的位置，其基本原理如圖1 所示。在 GNSS 無法單獨提供定位解的時候，利用影像提取若干測距信號，進行聯合定位解算。

圖1 衛星導航與攝影測量緊耦合定位技術原理

目前已有 GNSS 和偽衛星等地基增強手段融合定位的先例。對于視覺而言，可以將相片上的特征點當做“視覺基站”。如果這些特征點在世界坐標系下的 3 維坐標已知，則可通過測量相片來確定用戶到目標的距離，此時相機也變成了 1 種測距設備。如果被攝目標在世界坐標系下的坐標已知，并且可以測量被攝目標到用戶的距離，那么被攝目標相當于1 個基站或者偽衛星，稱作“視覺基站”。聯合處理GNSS 信號和視覺基站的信號，可以實現信號層面的聯合定位，稱為衛星導航與攝影測量的緊耦合定位（如圖2 所示）。緊耦合定位的過程主要分 2 個步驟，即從視覺影像中提取距離觀測值，再與GNSS 聯合定位解算。

圖2 利用攝影測量的方法測量終端到“視覺基站”的方法示意

1.1 利用視覺影像提取距離觀測值

根據影像覆蓋范圍內一定數量分布合理的像控點（已知其像點和地面點的坐標），利用共線條件方程求解像片外方位元素θ=[XS, YS, ZS,ψ,ω,κ]T。在求解外方位元素前，需要利用格網標志點對相機的內方位元素進行精確標定，以削弱鏡頭畸變帶來的影響[13]。在后續論述中，假設相機已經事先完成了內參數的標定并對鏡頭畸變進行了合理的校準。

如圖2 所示，物方已知點A和相機投影中心S在地面攝影測量坐標系中的坐標分別是（XA ,YA,ZA）、（XS,YS,ZS）；物方已知點A在相片上對應的點a在像空間坐標系中的坐標是（x,y,-f）。由共線條件方程知，物方已知點的觀測方程[14]可表示為

為保證參數估計的精度和可靠性，需要測量4 個或更多像控點和對應像點的坐標，采用最小二乘平差方法解算。此時像點坐標（x,y）作為觀測值，可列出每個像點的誤差方程為

利用最小二乘法求解相機外方位元素為

外方位元素的求解精度與物方距離遠近有關。在相機分辨率一定的條件下，相機和物方距離越遠，物方分辨率越低，像點觀測精度越低，外方位元素求解精度越低，位置求解精度越差。此時可利用求解的相機近似坐標和相片目標點的準確坐標計算相機至目標點的距離，這樣就利用相片形成了若干個到目標點的距離觀測值。利用相片提取距離觀測值的流程如圖3 所示。在求解相機外方位元素后，即可反算若干個相機到物方特征點之間的近似距離。該距離觀測值的方差可根據觀測距離遠近建立經驗模型確定。

圖3 利用相機求解相機到目標點距離算法流程

1.2 緊耦合定位方法

在可見衛星數不足的條件下，單獨使用GNSS無法實現定位，此時可聯合相機計算得到的距離觀測值和 GNSS 觀測信號求解用戶坐標。聯合影像與GNSS 定位求解過程為

式中：PG和PC分別為GNSS 測量的偽距和相機測量的距離；ρ為衛星或者視覺基站和接收機之間的幾何距離（以米為單位）；δorb為 GNSS 衛星軌道誤差；c為真空中的光速；分別為衛星和接收機的時鐘誤差；Ii和δtrop分別為第i個頻率信號的電離層延遲和對流層延遲； ?Pi和 ?C分別為GNSS 偽距測量誤差和相機測距誤差。

GNSS 信號受到多種誤差源的影響，但其測距精度與用戶位置基本無關。相機通過視覺測距的方法得到的距離觀測值，基本不受其他誤差的影響，但其觀測精度與物方距離有關，距離越遠，測距精度越差。

對GNSS 信號而言，采用標準定位方法時，即可忽略軌道誤差；衛星鐘差通過廣播星歷修正；電離層、對流層誤差均利用經驗模型修正；用戶坐標和接收機鐘差利用參數估計。通過這種方法，可以獲得米級的GNSS 定位精度。

相機距離觀測值僅和用戶坐標有關，無需估計鐘差參數，將幾何距離ρ按泰勒級數展開，可得

式中：ρ0為用戶接收機到衛星或視覺基站的近似幾何距離；ε為非線性誤差；為第i個衛星或視覺基站的坐標；(dx,dy,dz)為用戶接收機坐標的增量。忽略式（6）的非線性誤差項后可得

式中E(·)為數學期望運算符。利用泰勒級數線性化后，GNSS 觀測信號和相機觀測數據緊耦合的聯合定位問題可近似地轉化為 1 個線性問題，該線性系統為

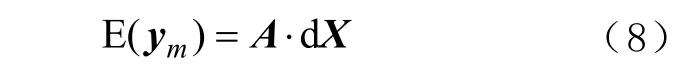
式中：前m個觀測值為 GNSS 距離觀測值；后n個觀測值為相機距離觀測值。

對應求解的4 個參數分別為用戶3 維坐標和GNSS 接收機鐘差。此方程的最小二乘解為

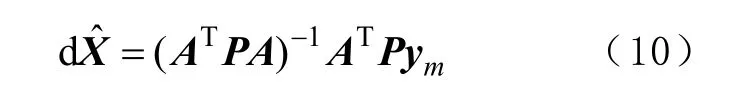
2 實驗與結果分析

為驗證上述方法的正確性，進行了仿真計算。仿真計算的場景如圖4 所示。仿真計算使用了3 顆可見的GNSS 衛星，聯合1 張包含4 個特征點的影像。

圖4 仿真計算場景示意

仿真過程中，相機焦距設為100 mm，相機內參數經過預先標定。為了研究物方距離對定位的影響，采用1 張真實照片，計算其外方位元素后固定相機位置，根據需求變換物方距離，解算出仿真的物方坐標。利用仿真的物方坐標研究物方坐標遠近對其定位精度的影響。進一步仿真了3 顆可見的 GNSS 衛星和對應的偽距觀測值。GNSS 偽距觀測值的精度為0.3 m，其他誤差在仿真過程中忽略不計。筆者比較了不同物方距離條件下，聯合GNSS 信號和相機測距信號求解坐標的精度，如圖5 所示。

圖5 不同物方距離條件下定位精度比較

圖5 顯示利用GNSS 與相機測距信號能夠顯著提高定位精度。為了量化定位精度，筆者對仿真采用的近100 個算例的定位精度進行了統計，其均方根誤差（root mean squares, RMS）如表1 所示。

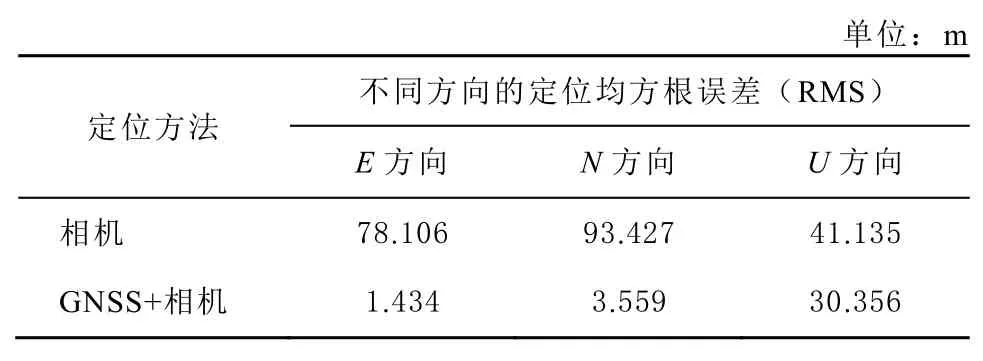
表1 相機定位與GNSS+相機緊耦合定位精度對比

表1 表明：在仿真的條件下，使用單GNSS無法定位，但與相機組合后，可使東西（E）和南北（N）方向平均定位精度從80～90 m 提升至1～4 m；高程（U）方向提升沒有平面明顯，也可將平均定位精度從41 m 精度提升至30 m 左右。

3 結束語

本文提出了 1 種視覺和 GNSS 緊耦合的定位技術，可提升 GNSS 在復雜場景下定位服務的可用性和抗干擾性。該方法的思路是利用相方坐標和物方坐標之間的相似關系，利用若干物方已知點求解相機的近似坐標，再反算相機到已知點之間的距離。受到相機分辨率的限制，在室外場景進行遠距離定位時，視覺定位精度不高。利用影像反算得到的距離觀測值，聯合少量的 GNSS 距離觀測值進行定位：一方面，視覺與GNSS 緊耦合定位的方式可以提升視覺定位的精度；另一方面，利用影像獲取的距離觀測值可以作為 GNSS 測距信號的補充，在GNSS 單獨無法定位時，聯合影像測距的方式即可實現用戶定位，提升了導航定位服務的可用性。仿真計算結果表明，聯合GNSS 測距信號與相機緊耦合定位，能夠有效地提升相機遠距離定位的精度，同時在 GNSS 系統可見衛星數不滿足定位條件時，仍可提供有效的定位結果。同時，仿真計算結果也驗證了本文所述方法原理上的可行性。在城市峽谷等區域，目前單獨依靠GNSS 技術無法提供連續可靠的定位結果，但如果利用 3 維實景城市模型輔助，提供物方特征點坐標，再利用本文所述的方法，則有望提升衛星導航定位服務的可用性。