基于VMD-LSSVM的月徑流預測方法研究

呂晗芳，趙雪花，桑宇婷，祝雪萍，張麗娟

(太原理工大學水利科學與工程學院，太原 030024)

0 引 言

徑流預測是水資源管理、調度和高效利用的基礎[1]。徑流過程是一個涉及水文、氣象及力學等的復雜過程，既受確定性因素的作用又受隨機因素的影響[2]，并呈現出非線性、非平穩性的特點。隨著計算機技術和數學算法的不斷發展，涌現出了一大批與機器學習和人工智能方法結合的研究。Suykens在傳統支持向量機(Support Vector Machines，SVM)的目標函數中引入誤差平方和項，并提出最小二乘支持向量機(Least-Square Support Vector Machines，LSSVM)方法，該方法收斂精度高，具有較好的非線性擬合能力[3,4]。目前最小二乘支持向量機在信號處理和時間序列預測等領域得到了廣泛應用，周秀平[5]將LSSVM-馬爾科夫鏈組合模型成功應用于年徑流預測；張楠[6]利用最小二乘支持向量方法，構建了基于多因子量化指標的徑流預測模型。

然而，僅用一個預測方法建立的預報模型很難反映水流序列的變化機制，這樣的單一模型會丟失隱含在原始序列中的重要信息。有研究指出，徑流時間序列的預處理對于提高預測精度是十分必要的。因此，當前提高精度的關鍵在于對數據的預處理，充分挖掘有限樣本包含的信息，并提取反映其變化規律的成分，再對這些成分建立模型，進而形成組合預測的建模思路以提高預測精度[7]。

小波分析、經驗模態分解(Empirical Mode Decomposition，EMD)和完備總體經驗模態分解法(Complete Ensemble Empirical Mode Decomposition with adaptive noise，CEEMDAN)是基于信號分析的分解方法，已常見于徑流數據的預處理階段。小波分析具有良好的時頻局域化特性，但自適應差且受人為因素影響較大；EMD自適應強，卻存在端點效應和過包絡等問題；CEEMDAN減小了白噪聲引起的誤差，但分解后會存在虛假模態，影響算法的精確度[8-11]。為了解決上述分解方法出現的問題，Dragomiretskiy[12]提出了是一種新的信號分解方法----變模態分解(Variational Mode Decomposition，VMD)[13-14]。相比EMD的遞歸篩選模式，VMD是一種完全非遞歸的變分模態分解，具有堅實的理論基礎，表現出更好的噪聲魯棒性。本文采用VMD對汾河上游月徑流數據進行預處理，分解出一系列含有單一頻率信息的分量，再對這些分量建立LSSVM預測模型，最后重構預測分量得到徑流預測結果，并對結果進行分析以驗證該方法的有效性。

1 模型與方法

1.1 變分模態分解(VMD)

VMD的目標是將原始信號分解為一系列具有特殊稀疏性的離散模態分量，該方法能夠自適應地確定相關波段并同時計算各模態分量，并更好的平衡解決各部分存在的噪聲。構造變分模型和求模型最優解的主要步驟如下：

(1)對模態函數進行Hilbert(希爾伯特)變換，并在得到的單側頻譜中加入各模態的中心頻率，使得解析信號轉換為其對應的基頻帶信號。計算該信號的梯度平方L2范數，并定義它為各模態分量的帶寬，此時VMD模型轉化為約束變分問題。

(1)

式中：x為徑流序列；uk為模態分量；ωk為模態的中心頻率；k為模態分量數；t為時間變量。

(2)在求解模型時，引入二次懲罰函數項和拉格朗日乘子算子，將上述約束變分問題轉化為非約束變分問題，并運用乘子交替方向法求解模型計算最優解。

L({uk},{ωk},λ)=

(2)

(3)最終，各模態分量解得，

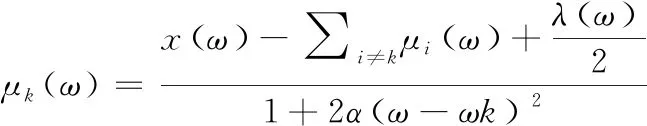
(3)

式中：λ為拉格朗日乘子；α為二次懲罰系數；i和k為模態分量數。

(4)根據式(3)不斷更新ukωkλ，直到滿足約束條件：

(4)

式中：ε為預先設置的極小值實數，本文取值10-7。

1.2 最小二乘支持向量機(LSSVM)

最小二乘支持向量機(LSSVM)是對支持向量機(SVM)的改進，其代替傳統二次規劃方法解決函數估計問題，引入最小二乘線性系統到支持向量機中，具體步驟如下：

(1)對于給定訓練樣本集{xi,yi}，其中i=1,2,…,N，xi為輸入數據，yi為輸出數據，應用核函數將樣本轉換到高維空間中，則樣本滿足線性規律：

f(x)=βTφ(x)+b

(5)

式中：βT為高維空間超平面的法向量；b為偏置量；φ(x)為非線性映射函數。

(2)依據結構風險最小化原理，將回歸問題轉化成一個等式約束的優化問題：

(6)

式中：ei為誤差；γ為正則化參數。

(3)針對目標函數建立拉格朗日等式：

(7)

式中：θ為拉格朗日乘子。

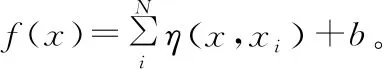
1.3 VMD-LSSVM預測模型

由于VMD處理復雜信號的突出優勢，本文嘗試建立VMD-LSSVM組合預測模型以提高復雜徑流序列預測的精度，其模型結構如圖1所示。具體模型計算步驟如下：

(1)各站點的月徑流時間序列總長516，首先經過EMD、CEEMDAN和VMD分解，可得到一系列具有單一頻率信號的固有模態函數(IMF)，即為圖中IMF1,IMF2,…,IMFn，VMD法的分解個數設定與CEEMDAN的分解個數相同，選擇二次懲罰系數為2 000，噪聲容忍度為0。

(2)將一系列IMF分別輸入LSSVM中，使用網格搜索進行最優調參并加入歸一化提高擬合度，得到各IMF對應的輸出值序列，即為圖中Y1,Y2,…,Yn。

(3)各輸出值重構為最終的預測徑流序列。

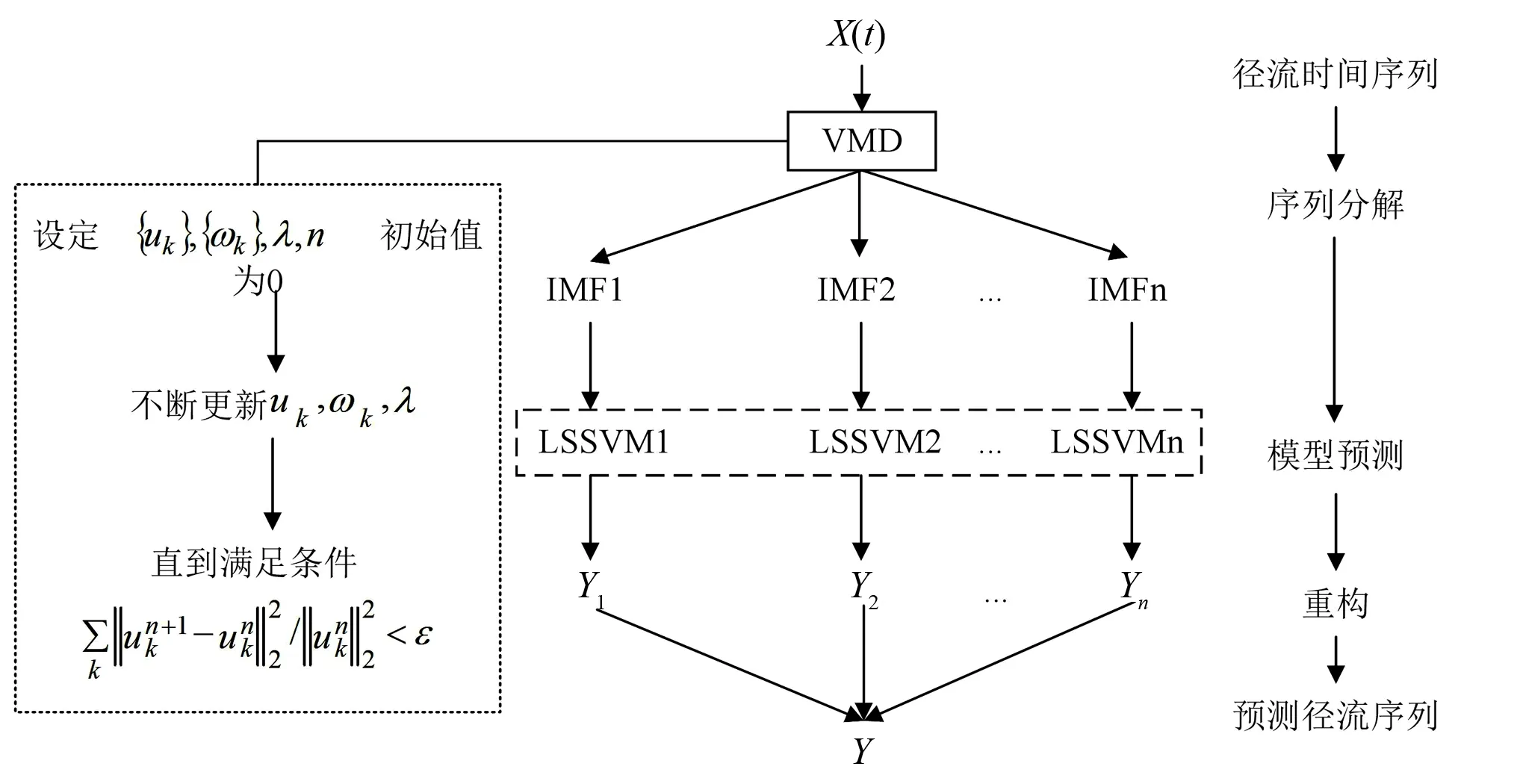
圖1 VMD-LSSVM模型預測流程圖Fig.1 Flowchart of the VMD-LSSVM model proposed

2 實例分析

汾河作為山西的母親河，是黃河的第二大支流，位于黃河的中游段，流域面積達38 728 km2。汾河的上游段從寧武縣的管涔山河源到太原北郊的蘭村，是太原重要的水源地和最大的飲用水功能區，本文研究的4個水文站點均位于汾河上游。上靜游站位于汾河支流嵐河上，此站上游控制面積為1 140 km2；汾河水庫站處于嵐河與汾河的交匯處；寨上站坐落于古交市寨上村，控制面積約1 500 km2；蘭村站在汾河的中上游，位于太原市西北22.5 km的上蘭村。4個水文站1958-2000年月徑流數據資料來自山西省水文局，已被運用于多個科研項目及工程，因此可以保證可靠性；且該徑流序列較長，資料精度較高，具有很好的代表性，能夠客觀反映汾河上游徑流演變特征。

2.1 月徑流資料VMD分解

利用VMD法對4個水文站的月徑流資料進行分解，各站原始徑流序列和其分解IMF分量的頻譜圖如圖2所示。原始徑流數據包含多頻率的徑流序列信息，呈現“雜亂無章”的特點，很難找到其中蘊含的變化規律。隨著頻率的增大，原始徑流序列的幅值變化出現多個峰值，代表在某段頻率周期中徑流序列出現了大幅度變化，相較其他的小幅變化這種變化能夠主導序列的趨勢，這類峰值變化信息為主要頻率信息，包含主要頻率信息的分量為主要頻率分量。而VMD法分解出的各IMF分量能夠將原始序列的多個頻率分解開來，并且這些預處理后的分量能夠自適應的提取重要變化信息。蘭村站的IMF1、IMF3、IMF4、IMF6與其他站點的IMF1、IMF2、IMF4、IMF6分別包含了各主要頻率信息，剩余的IMF包含其他相關信息。各IMF分量在主要頻率信息的其余各處幅值基本為0，說明VMD可以在不影響重要信息的情況下自適應地去除不利于模型預測的噪聲，在分解與提取的同時體現了優秀的除噪效果，更突出了重要變化信息，使得原始數據變化過程易于讀取。

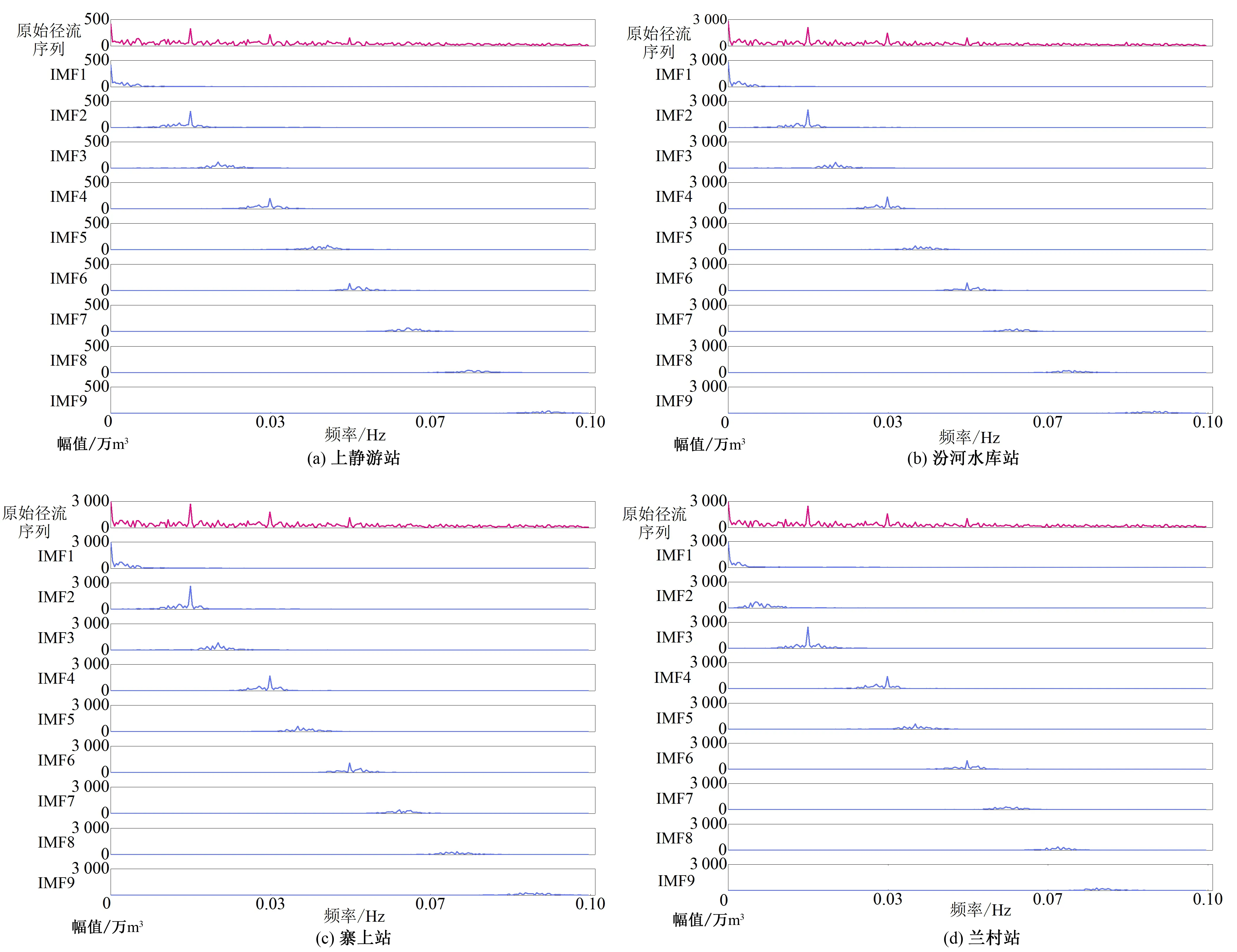
圖2 月徑流序列的VMD分解結果圖Fig.2 VMD decomposition results of monthly runoff series

2.2 預測結果分析

本文使用上靜游站、汾河水庫站、寨上站和蘭村站1958-2000年總計516個月徑流資料，其中前492個數據即1958年1月至1998年12月徑流資料為訓練集，這組數據用于模型模擬及訓練，后24個數據即1999年1月至2000年12月徑流資料為測試集用于測試模型預測效果。

為對比模型預測效果，本文選擇4種模型進行分別預測，包括單一預測LSSVM模型、組合預測EMD-LSSVM模型、CEEMDAN-LSSVM模型以及VMD-LSSVM模型。各模型預測結果與原徑流數據的對比見圖3。

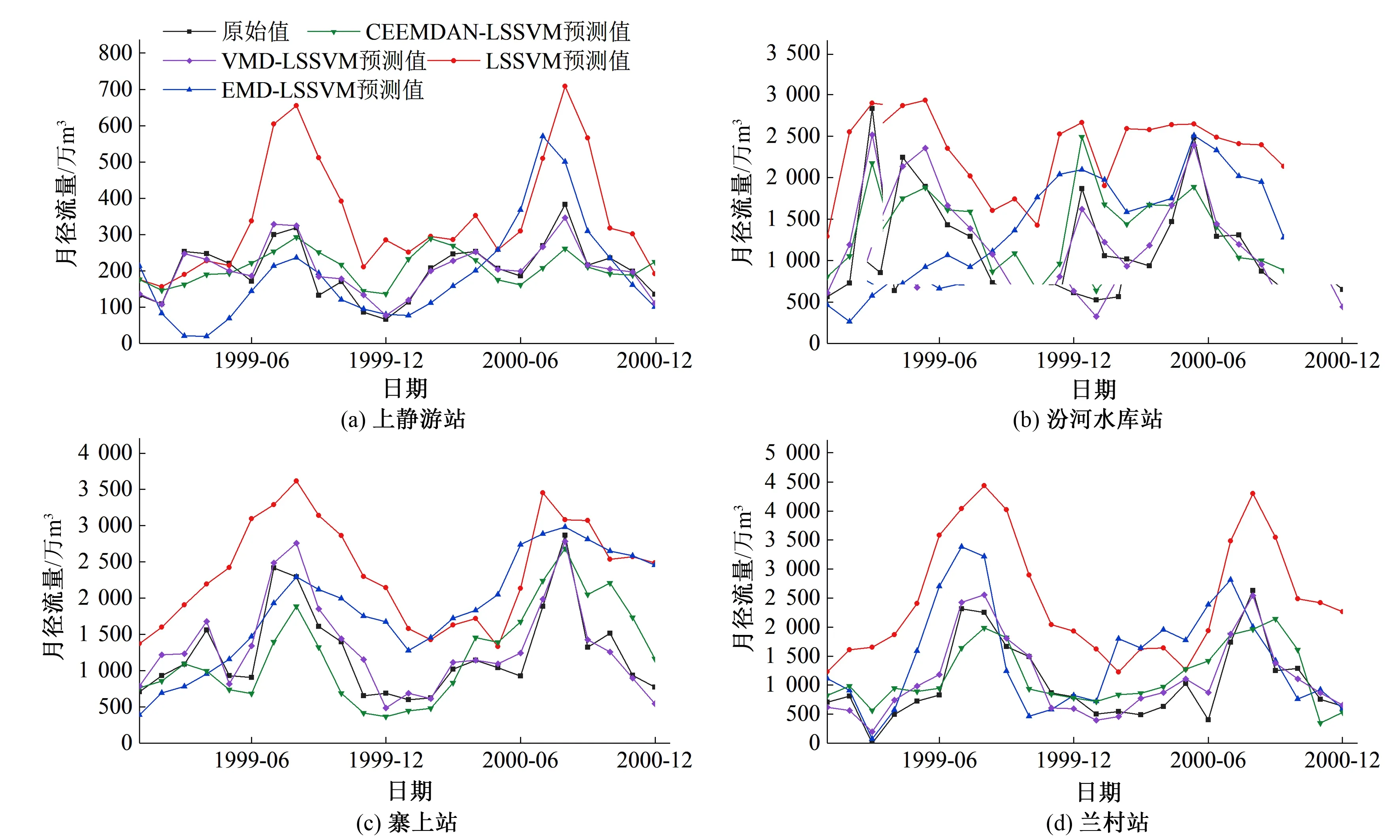
圖3 4個水文站各模型預測結果對比圖Fig.3 Forecast results by using each model at four hydrological stations

由圖3可知：①在單一LSSVM預測模型下，4個站點的預測效果并不理想，只能夠顯示出大致的變化趨勢，并且大部分預測數據比實測數據高60%左右，在4種模型中預測效果最差。其中最為明顯的是，上靜游站1999年6-10月與2000年7-9月預測值明顯遠大于實測值。②組合模型EMD-LSSVM的預測效果相較單一預測模型更好，更接近實測值，但仍有部分數據存在趨勢相反或誤差大于50%的情況。③在使用組合模型CEEMDAN-LSSVM時，預測結果的變化趨勢已基本與實測序列相同，誤差相較EMD-LSSVM模型減少了約40%，在4個模型中預測效果僅次于VMD-LSSVM模型，僅有個別數據存在誤差較大的情況。這說明CEEMDAN比EMD減少了模態混疊的現象，使預測效果得到提高。④組合模型VMD-LSSVM的預測效果與實測徑流曲線擬合度最好，變化趨勢與原序列相同，且無極端值出現，可以初步判斷，VMD分解方法較經驗模態系列方法能更好地應對序列中包含的復雜頻率信息，且與LSSVM組合應用效果更好。

為了更清晰地闡述模型預測效果，平均絕對誤差MAE、均方根誤差RMSE、平均絕對百分比誤差MAPE和納什效率系數NS4個指標將用于分析預測精度，計算公式如下：

(8)

(9)

(10)

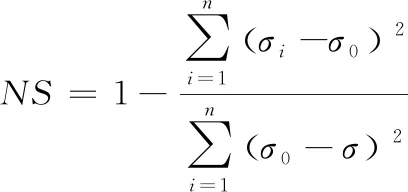
(11)

式中：σi為i時刻的預測值；σ0為i時刻的實測值；σ為實測值的均值。

根據《水文情報預報規范(GB/T 22482-2008)》的規定，當NS≥0.90時，預測精度為甲級；0.70≤NS<0.90時，預測精度為乙級；0.50≤NS<0.70時，預測精度為丙級。

表1為汾河上游4個水文站的精度指標結果，從中可以分析得到：①各模型在訓練期的NS指標為0.7以上，達到丙級以上水平，且隨著模型的優化，從單一預測模型到組合預測模型，從應用遞歸的經驗模態系列方法到應用非遞歸、分解更完全的變分模態分解方法，MAE、MAPE和RMSE指標逐漸減小，NS逐漸靠近1。②測試期預測結果關于模型的比較更加明顯，VMD-LSSVM模型的MAE、MAPE和RMSE與單一LSSVM模型相比分別減少了80%～90%、75%～90%、50%～90%；與EMD-LSSVM模型相比分別減少了70%～80%、60%～85%、50%～80%；與CEEMDAN-LSSVM模型相比分別減少了50%～75%、40%～70%、40%～70%。VMD-LSSVM模型的NS為0.81～0.92，預測精度為甲級；EMD-LSSVM模型的NS為0.50～0.68；CEEMDAN-LSSVM模型的NS為0.69～0.83；LSSVM模型的NS為0.21～0.31，預測結果不可信。③訓練期整體比測試期預測效果要好，各模型都存在不同程度的過學習現象。以寨上站為例，LSSVM模型測試期RMSE為訓練期的近10倍，而VMD-LSSVM模型測試期RMSE為訓練期的3倍。LSSVM單一模型對訓練樣本內的噪聲和孤立點比較敏感，由于徑流序列的復雜多頻特性，其含有的不利噪聲表現為頻譜圖中各個頻率段摻雜的無序低幅值波動，這會影響LSSVM的回歸擬合，而VMD分解能夠使復雜信息轉化為主要頻率信息和其他信息，并且有優秀除噪效果，有利于LSSVM尋找最優回歸參數以降低輸出誤差，所以將分解后的IMF分量再輸入LSSVM進行預測能夠減少噪聲對模型預測精度的影響。④整體來看，上靜游站和蘭村站的VMD-LSSVM模型預測效果最為理想，NS達到甲級，而汾河水庫站與寨上站的預測精度最高只能達到乙級。

表1 4個水文站各模型預測誤差對比Tab.1 Prediction error of each model at four hydrological stations

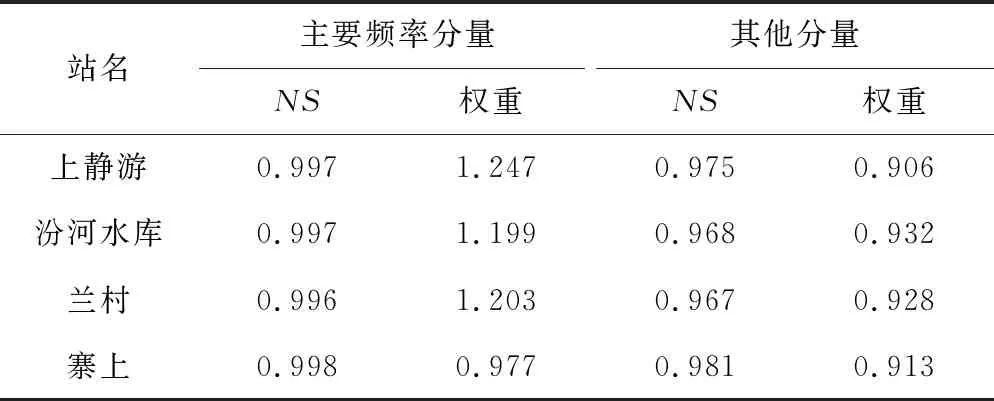
表2 4個水文站兩類分量的預測誤差及權重對比Tab.2 Prediction error and weight of each types of components at four hydrological stations

為了更加深刻地描述VMD分解方法在預測中的應用效果，做出4個水文站兩類分量的預測誤差及權重對比(見表2)。通過VMD法分解后可以得到各站的IMF分量，提取出各站的主要頻率分量與其他頻率分量，對這組原始數據與預測數據進行NS誤差分析，并計算兩類分量的線性權重。主要頻率分量的NS接近1，預測精度高，而其他頻率分量精度稍低，并且主要頻率分量較其他頻率分量在預測序列中權重大，說明主要頻率分量在預測中有重要地位，該分量精度的提升可以帶動總體VMD-LSSVM模型精度的提高，研究這類信息的提取和預測對于提高整體預測精度具有重要意義，這也表明了VMD-LSSVM組合模型對于月徑流序列預測的優勢所在。

綜上所述，汾河上游徑流序列的預測效果優劣排序應如下：VMD-LSSVM > CEEMDAN-LSSVM > EMD-LSSVM > LSSVM，組合模型較單一預測模型在預測精度上有一定的優勢，其中VMD-LSSVM模型相較EMD-LSSVM和CEEMDAN-LSSVM在訓練期和測試期都能達到較高精度，該模型用于復雜多頻信息的徑流序列預測是可行、有效的。

3 結 語

(1)在對復雜的徑流序列進行預測時，單一LSSVM模型的預測結果不可信，需要將序列進行預處理后再預測，經過分解后進行預測再重構的組合模型法可以大幅提高預測精度。

(2)相比經驗模態系列方法的遞歸篩選模式，變模態分解法是一種完全非遞歸的變分模態分解，具有堅實的理論基礎，能夠提取出主要頻率信息，表現出更好的噪聲魯棒性，從而有利影響預測效果，進一步提高預測精度。

(3)VMD-LSSVM模型首先將實測徑流數據分解為一系列子序列，并提取出主要頻率分量和其他相關信息，再把該組序列分別輸入LSSVM進行預測，得到對應的一組預測序列，經重構后為最終的預測數據。該方法的預測效果與EMD-LSSVM、CEEMDAN-LSSVM和LSSVM相比誤差最小，NS為乙級以上。VMD-LSSVM模型用于包含多頻率信息的復雜徑流序列預測是可行且有效的，該模型可以推廣到與汾河上游地理環境相似的流域。

□