基于粒子群算法的RBF 徑向基神經(jīng)網(wǎng)絡(luò)教學(xué)質(zhì)量評(píng)價(jià)模型

劉鵬，賈文雅

（山西藥科職業(yè)學(xué)院，太原 030031）

0 引言

為了高質(zhì)量完成高職教育立德樹人的根本任務(wù)，為黨和國家培養(yǎng)高素質(zhì)技能型人才，全面提高教學(xué)質(zhì)量意義重大，教學(xué)質(zhì)量評(píng)價(jià)科學(xué)準(zhǔn)確刻不容緩，勢(shì)在必行。采用信息化手段，應(yīng)用到當(dāng)今的課堂教學(xué)中，是貫穿教育改革的十分重要的步驟，也是教師改進(jìn)工作手段的核心要求。它的教學(xué)質(zhì)量直接影響著整個(gè)學(xué)校的質(zhì)量。尤其在疫情期間，搞好線上信息化教學(xué)尤為重要。而目前，高職傳統(tǒng)教學(xué)質(zhì)量評(píng)價(jià)中普遍存在“評(píng)價(jià)模糊化，方法單一化”、“碎片改革多，系統(tǒng)構(gòu)建少”、“教學(xué)信息溝通不暢”等問題，這些都已成為高職教育持續(xù)健康發(fā)展的瓶頸。為此，運(yùn)用科學(xué)的方法對(duì)課堂教學(xué)質(zhì)量進(jìn)行全面、合理的評(píng)價(jià)，對(duì)于評(píng)價(jià)學(xué)校的教學(xué)水平和教學(xué)質(zhì)量具有重要意義。然而，單純的對(duì)教學(xué)水平和教學(xué)質(zhì)量進(jìn)行評(píng)價(jià)，相關(guān)的工作量大、統(tǒng)計(jì)復(fù)雜，很難形成系統(tǒng)的評(píng)價(jià)體系，因此，一些教學(xué)質(zhì)量評(píng)價(jià)工作往往流于形式，必要尋求一種新的科學(xué)的評(píng)價(jià)方法。近年來，一些學(xué)者考慮利用神經(jīng)網(wǎng)絡(luò)，提升相關(guān)評(píng)價(jià)標(biāo)準(zhǔn)的準(zhǔn)確性。因?yàn)樯窠?jīng)網(wǎng)絡(luò)算法具有很強(qiáng)的非線性函數(shù)逼近能力，對(duì)相關(guān)模糊指標(biāo)的或不準(zhǔn)確的參數(shù)，有較好的分析能力。但是，由于神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程較為復(fù)雜，需要較多先驗(yàn)知識(shí)，對(duì)操作者有較高的要求。因此，將神經(jīng)網(wǎng)絡(luò)引入到教學(xué)質(zhì)量的評(píng)價(jià)中，結(jié)果存在不準(zhǔn)確的問題。

本文考慮到神經(jīng)網(wǎng)絡(luò)在教學(xué)質(zhì)量評(píng)價(jià)中的進(jìn)展和局限性，引入粒子群算法對(duì)原有神經(jīng)網(wǎng)絡(luò)模型進(jìn)行優(yōu)化，根據(jù)教學(xué)評(píng)估信息大量存在的特點(diǎn)，以及粒子群算法改進(jìn)神經(jīng)網(wǎng)絡(luò)是模糊邏輯和神經(jīng)網(wǎng)絡(luò)的結(jié)合，集合各自的優(yōu)勢(shì)，集學(xué)習(xí)、聯(lián)想、識(shí)別、自適應(yīng)和模糊信息處理特性于一體。本文采用粒子群改進(jìn)神經(jīng)網(wǎng)絡(luò)對(duì)教學(xué)質(zhì)量進(jìn)行評(píng)價(jià)。

1 基于粒子群算法的神經(jīng)網(wǎng)絡(luò)教學(xué)評(píng)價(jià)模型

1.1 粒子群算法

粒子群算法（PSO）是一種進(jìn)化計(jì)算，是一種類似于遺傳算法的迭代優(yōu)化工具。粒子群算法模擬鳥類的捕食行為。你可以想象這樣一個(gè)場(chǎng)景：一群鳥隨機(jī)搜尋食物。在這個(gè)地區(qū)，只有一種食物，然而所有的鳥都不知道食物在哪里，但它們清楚的知道到食物之前的距離。怎么才能形成最優(yōu)覓食策略呢？當(dāng)前較為簡單、有效的方法是從鳥食周圍的區(qū)域?qū)ふ沂澄铩ＡＷ尤核惴◤脑撃Ｐ椭械玫浇鉀Q此類問題的啟示。每一次優(yōu)化都是為了在空間中搜索一只被稱為“粒子”的鳥。所有粒子都有由優(yōu)化函數(shù)確定的適應(yīng)值，每個(gè)粒子也有一個(gè)速度來確定方向和距離。然后粒子跟隨優(yōu)化粒子搜索粒子群，將其作為一個(gè)隨機(jī)粒子（隨機(jī)解）進(jìn)行搜索，采用迭代的方法尋找最優(yōu)解。在每次迭代中，粒子通過跟蹤兩個(gè)“極端”粒子進(jìn)行自我更新。第一個(gè)是粒子找到的最優(yōu)解。這類解被稱為PBest，另一種方法是按物種尋優(yōu)。這類解被稱為全局極值。

當(dāng)找到這兩個(gè)最優(yōu)解時(shí)，粒子通過公式（1）和公式（2）進(jìn)行自我更新，以定位自己的速度和位置。

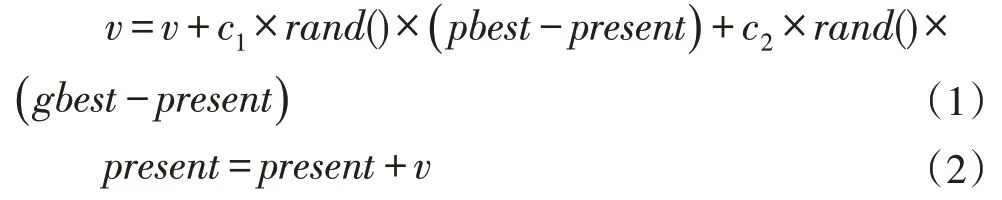
其中v 是粒子的速度，Present 是粒子當(dāng)前的位置。rand（）是（0,1）中的隨機(jī)數(shù)。C1,C2是學(xué)習(xí)因子，通常C1=C2=2。任何維度的速度都受最大速度的限制，如果更新后的速度超過Vmax，則速度為Vmax。

1.2 RBF神經(jīng)網(wǎng)絡(luò)

徑向基函數(shù)是一個(gè)實(shí)值函數(shù)，它的值只取決于到原點(diǎn)的距離，因此Φ(x)=Φ(||x||)；或者，也可以取決于到另一個(gè)點(diǎn) c 的距離，稱為中心，那么有φ(x,c)=φ(||x-c||)。任何滿足性質(zhì)φ(x)=φ(||x||)的函數(shù)φ都是徑向函數(shù)。范數(shù)通常是歐幾里得距離。

徑向基函數(shù)通常用于建立以下形式的函數(shù)：

這種近似函數(shù)y(x)的計(jì)算結(jié)果，可以看成N 個(gè)徑向基函數(shù)的總和，每個(gè)徑向基函數(shù)與不同的中心ci相關(guān)聯(lián)，并且由適當(dāng)?shù)臄?shù)wi加權(quán)。這種近似方法特別適用于表現(xiàn)出足夠簡單混沌行為的非線性系統(tǒng)的時(shí)間序列預(yù)測(cè)和控制、計(jì)算圖形學(xué)中的三維重建（例如分層RBF）。

有三個(gè)學(xué)習(xí)參數(shù)：RBF 中心CK、σk、Wk。算法流程如下：

（1）從輸入矩陣中選擇一個(gè)系列Ck；

（2）計(jì)算方差

式中，dmax是最大距離，K 是Ck的個(gè)數(shù)；

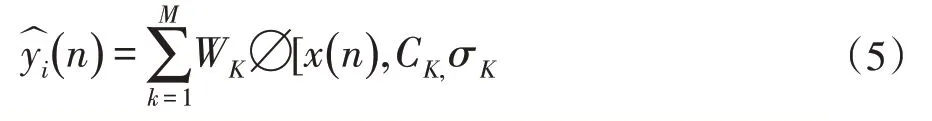
圖1 RBF神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

（4）更新 RBF 參數(shù)

其中yd(n)是失效輸出；μN(yùn),μC,μσ是三個(gè)參數(shù)的映象。

（5）如果網(wǎng)絡(luò)收斂，則停止計(jì)算，否則轉(zhuǎn)到步驟（3）。具體步驟見圖2。

1.3 用粒子群算法訓(xùn)練BBPP神經(jīng)網(wǎng)絡(luò)

PSO 算法對(duì)BP 神經(jīng)網(wǎng)絡(luò)的優(yōu)化是用梯度下降法來訓(xùn)練權(quán)值和閾值。關(guān)鍵是建立連接維度空間和神經(jīng)網(wǎng)絡(luò)的權(quán)重與閾值之間的映射關(guān)系。本文的學(xué)習(xí)過程主要是權(quán)值和閾值的更新過程。BP 算法中的權(quán)值和閾值對(duì)應(yīng)于粒子的位置。

粒子的適應(yīng)度函數(shù)是最小均方差MSE

其中N 是輸出矩陣的維數(shù)；P 是樣本數(shù)。粒子群算法訓(xùn)練神經(jīng)網(wǎng)絡(luò)權(quán)值的步驟如下：

（1）對(duì)神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)進(jìn)行建模，包括輸入層、隱藏層、輸出層和神經(jīng)元數(shù)目。

（2）初始粒子群。

（3）適應(yīng)度函數(shù)的確定。

（4）根據(jù)公式（3）計(jì)算適應(yīng)度；

（5）更新 pBest 和 gBest；

（6）更新w。

（7）更新任意粒子的速度和位置，確定最優(yōu)解。

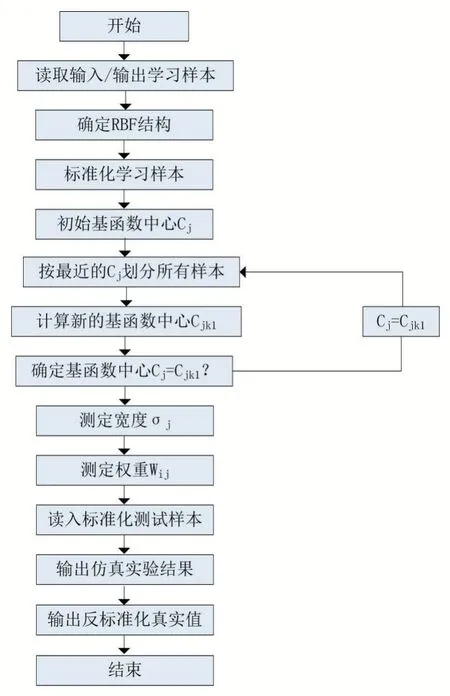
圖2 RBF神經(jīng)網(wǎng)絡(luò)流程圖

2 教學(xué)質(zhì)量評(píng)價(jià)模式

2.1 評(píng)價(jià)指標(biāo)體系

根據(jù)該指標(biāo)體系，影響教學(xué)質(zhì)量的主要指標(biāo)為12個(gè)（見表1），因此可以采用12 個(gè)輸入層數(shù)，準(zhǔn)確計(jì)算合理的輸入模式，是設(shè)計(jì)神經(jīng)網(wǎng)絡(luò)模型的關(guān)鍵因素。一旦設(shè)計(jì)不合理，輸入神經(jīng)元較多，會(huì)導(dǎo)致模型結(jié)構(gòu)越復(fù)雜，訓(xùn)練周期長。否則，很難得到非線性關(guān)系。

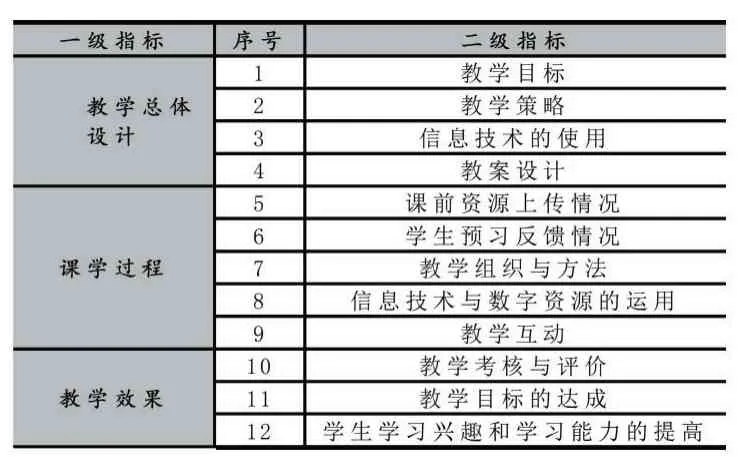
表1 藥學(xué)專業(yè)信息化教學(xué)學(xué)生評(píng)教綜合評(píng)價(jià)指標(biāo)

2.2 訓(xùn)練神經(jīng)網(wǎng)絡(luò)

輸入層數(shù)為12 層，隱藏層數(shù)為10 層，輸出層數(shù)為1 層，結(jié)構(gòu)為 12-10-1。

Dimsize 賦值為 141，popsize 賦值為 25，Wmax=0.9，Wmin=0.4，C1=C2=2，MSE 為 le-5，最大映象為10000。

2.3 實(shí)驗(yàn)結(jié)果

疫情期間，為準(zhǔn)確有效評(píng)價(jià)我院藥學(xué)專業(yè)所有課程在線教學(xué)的質(zhì)量，對(duì)500 份調(diào)查問卷進(jìn)行了測(cè)評(píng)。其中400 份問卷為訓(xùn)練樣本，100 份問卷為測(cè)試樣本，如表2 所示。

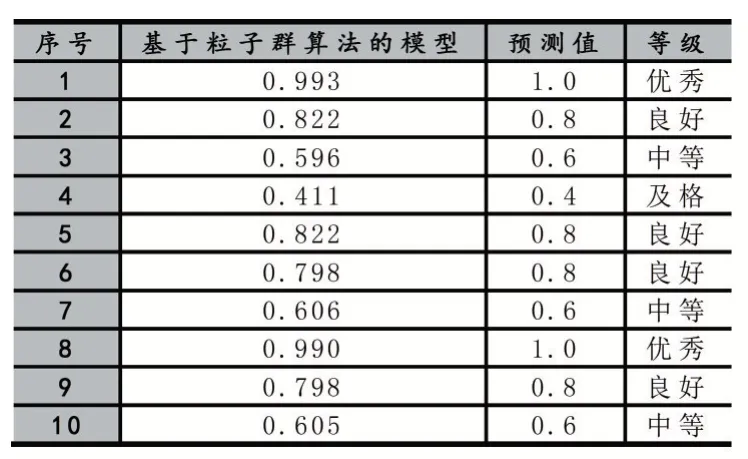
表2 檢測(cè)結(jié)果表

3 結(jié)語

（1）從表2 可以得出，該模型的結(jié)果中，計(jì)算得到的真實(shí)值和輸出值之間的誤差變化成負(fù)相關(guān)，結(jié)果越小導(dǎo)致訓(xùn)練樣本越多，數(shù)學(xué)模型描述教學(xué)質(zhì)量的好壞的作用也越明顯。

（2）引入PSO 后的神經(jīng)網(wǎng)絡(luò)，可以大幅度降低神經(jīng)網(wǎng)絡(luò)計(jì)算時(shí)間，尋優(yōu)結(jié)果也更準(zhǔn)確，一旦涉及模糊神經(jīng)網(wǎng)絡(luò)，相關(guān)結(jié)果也是可以預(yù)見的，教學(xué)管理人員可以實(shí)時(shí)調(diào)整模型的相關(guān)參數(shù)，在一定程度上解決了神經(jīng)網(wǎng)絡(luò)的盲目性問題。

（3）綜上所述，本模型不失為評(píng)價(jià)教學(xué)質(zhì)量的一種良好方法。