奇異攝動問題在修正的Bakhvalov-Shishkin網格上的混合差分格式

鄭權，劉穎，劉忠禮

（1.北方工業大學理學院，北京100144； 2.北京聯合大學生物化學工程學院，北京 100023）

奇異攝動問題在諸多領域應用廣泛，例如河網水質問題的建模、對流熱傳輸問題、半導體器件模型的漂移擴散方程以及金融模型等。奇異攝動問題，即一個很小的攝動參數將導致其真解在邊界層區域劇烈振蕩，使得經典的差分方法無法得到滿意的結果。因此，奇異攝動問題的數值求解成了熱門研究課題[1-9]。

本文將考慮以下奇異攝動對流擴散方程的兩點邊值問題：

其中，ε是一個很小的攝動參數且 0＜ε? 1，A和B是給定的常數，b(x)，c(x)和f(x)是充分光滑的函數，且 滿足 0＜β＜b(x)＜β*，0 ≤c(x)＜γ*， 其中β，β*和γ*是常數。這些條件使得方程(1)存在唯一解u(x)， 且解在x=1 處存在一個邊界層[1]。

對奇異攝動問題層適應的數值解法研究已取得一系列重要進展。對于線性奇異攝動問題(1)，ROOS 等[2]證實了簡單迎風格式在Bakhvalov-Shishkin 網格上達到一階收斂，高于在Shishkin 網格上的近一階收斂，并列出了其他幾種網格函數，如多項 式 Shishkin 網格和 Vulanovi?改進的Shishkin 網格等，并給出了簡單迎風格式的相應收斂階數。STYNES 等[3]研究了c(x)≡0 時中點迎風差分格式在任意網格上的誤差估計，進一步研究了在Shishkin 網格上的一致收斂性，在粗網格上得到二階收斂，在細網格上得到近一階收斂，表明中點迎風格式在Shishkin 網格上的收斂階數優于簡單迎風格式；提出的在粗網格上利用中點迎風格式和在細網格上利用中心差分格式的混合差分格式方法，在粗網格和細網格上分別達到了二階和近二階收斂。梁克維等[4]研究了c(x)≡0 時方程的中點迎風格式在Bakhvalov-Shishkin 網格上的一致收斂性，得到了一階收斂的誤差估計。ZHENG 等[5]研究了中點迎風格式在Bakhvalov-Shishkin 網格上的一致收斂性，將粗網格上的一階收斂提高到二階收斂。ZHENG 等[6]還研究了帶權的混合差分格式在Bakhvalov-Shishkin 網格上求解擬線性奇異攝動方程以及估算導數的誤差，得到的解和導數的誤差都是二階的。此外，也有將層適應網格上的有限差分方法用于求解拋物型奇異攝動問題[7-8]以及橢圓型奇異攝動問題[9]等。

本文構造修正的Bakhvalov-Shishkin 網格，建立新混合差分格式求解問題(1)。第1 節證明關于奇異攝動問題的最大值原理并給出解的性質；第2 節研究混合差分格式在修正的Bakhvalov-Shishkin 網格上的一致收斂性；第3 節用數值算例驗證理論分析結果。

1 最大值原理以及解的性質

引理1假定u(x)是滿足u(0)≥0 和u(1)≥0的充分光滑的函數，若當x∈(0，1)時，Lu(x)＞ 0，則對于x∈[0，1]，有u(x)≥ 0。

證明令x*滿足假 設u(x*)＜0，顯然x*?{0，1}，因此

且

Lu(x*)=-εu″(x*)+b(x*)u'(x*)+c(x*)u(x*)≤ 0，與已知條件矛盾。

引理1 得證。

引理2（連續情形的最大值原理） 假定u(x)是滿足u(0)≥0 和u(1)≥0 的充分光滑的函數，若當x∈(0，1) 時 ，Lu(x)≥ 0，則 對 于x∈[0，1]，有u(x)≥ 0。

證明對于 ?δ＞ 0，令e-ax)，其中a為正常數，則有

且

由引理1，對于所有x∈[0，1]，有

令δ→ 0，則得引理 2。

證畢！

引理2 給出了問題(1)的連續最大值原理，表明問題(1)的解具有唯一性。

注本文補充了連續最大值原理的證明，對文獻[10]中的證明做了修正。

引理3[1]對于任意正整數q， 方程的解u(x)在[0，1]上可表示為

其中光滑部分S滿足

邊界層部分E滿足

q的取值取決于函數b(x)，c(x)和f(x)的 光 滑程度。

2 混合差分格式在修正的Bakhvalov-Shishkin 網格上的一致收斂性

2.1 網格函數

為了使中心差分格式在經典的Bakhvalov-Shishkin 網格[2，4-5]的邊界處得到較高的截斷誤差，在Bakhvalov-Shishkin 網格的轉折點的基礎上，選取另一轉折參數τ2=1-x3N/4=其中x3N/4是 Bakhvalov-Shishkin 網 格 上的i= 3N4 的一個結點，將區間 [1-τ2，1]均分成N4 個子區間。方便起見，仍將網格函數記為xi，則修正的Bakhvalov-Shishkin 網格如下：

引 理 4令hi=xi-xi-1， 則 有N-1≤hi＜。

2.2 混合差分格式

考慮在區間[0，1-τ2]上使用中點迎風格式以及在區間(1-τ2，1]上使用中心差分格式的混合差分格式：

即

2.3 一致收斂性

引理5（離散比較原理） 假定且是網格函數且滿足v0≤w0，vN≤wN和LN vi≤LN wi，i=1，2，…，N-1， 那么，對任意的i均有vi≤wi。

證明在引理5 的條件下，LN系數矩陣是一個(N-1)×(N-1)階對角占優矩陣，且對角線元素均為正、次對角線元素均非正，是一個不可約的M矩陣，因此算子LN滿足離散比較原理。

引理5 得證。

于是差分格式(3)在網格(2)上有唯一解，引理5中的函數wi稱為函數vi的障礙函數。

引理 6定義網格函數Z0=1，Zi=那 么 ，對 于i=1，2，…，N-1， 有

證明顯然有且D-Zi=因此

進而，注意到c(x)≥ 0 和b(x)＞β＞ 0， 由式(3)，有

引理6 得證。

引理7假設u(x)是定義在[0，1]上的充分光滑的函數，在修正的Bahkvalov-Shishkin 網格上，對于求解問題(1)和混合差分格式(3)的截斷誤差，存在常數C，使得

證 明當i=1，2，…，3N4 時 ，由 式 (1) 和式(3)，有

其中，

使用帶有積分型余項的泰勒展開式，有

當i= 3N4 +1，3N4 +2，…，N-1 時 ，由式(1)和式(3)，有

使用帶有積分型余項的泰勒展開式，有

引理7 得證。

引理8假定則在修正的Bakhvalov-Shishkin 網格上，對于方程(1)和混合差分格式(3)的解的光滑部分，存在常數C，使得

證明由引理7 和引理3 可得

令wi=C0N-1(ε+N-1)xi，i=0，1，…，N， 其中常數C0足夠大。那么

引理8 得證。

引理9假定在修正的Bakhvalov-Shishkin 網格上，對于方程(1)和混合差分格式(3)的解的邊界層部分，存在常數C，使得

證明對所有的t≥0，有et≥1+t。回顧引理6 中的函數Zi， 則有

由引理 3 和式(5)，有

令Yi=C0Zi ZN，i=0，1，…，N， 其中C0為足夠大的常數。由引理6 可得

由式(5)和引理 3 可得

因此，由引理5 可知，

結合式(6)和式(7)，有

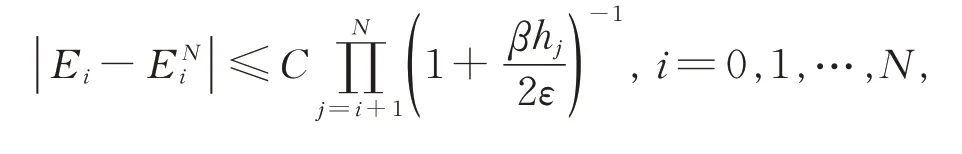
由引理4，有

再由式(8)，可得引理9。

引理9 得證。

引理10假定在修正的Bakhvalov-Shishkin 網格上，對于方程(1)和混合差分格式(3)的解的邊界層部分，存在常數C，使得

證明當i=N2 +1，N/2+2，…，3N4 時，由引理7 的證明，易得

因此，由式(9)、引理 3、式(2)、式(5)以及引理 4，有

當i= 3N4 +1，3N/4+2，…，N時，由引理 7、引理 3、引理 4 和式(5)，有

其中C0為足夠大的常數。由引理6 可得

當i= 3N4 時，

因此，

由于c(x)≥ 0，b(x)＞β＞ 0，則有

顯 然 有因此，由引理 5 可知，φi是的障礙函數。

引理10 得證。

定理1假定混合差分格式(3)在修正的Bakhvalov-Shishkin 網格(2)上求解問題(1)，滿足

證明由式(4)以及引理8～引理10 即可證得。

3 數值算例

例1考慮奇異攝動問題：

表1 為中點迎風格式在Bakhvalov-Shishkin 網格上和混合差分格式在Shishkin 網格上的數值結果，其中，用計算誤差精度，用計算收斂階數，計算收斂常數 。對于i＞N2，混合差分格式在Shishkin 網格上、中點迎風格式在Vulanovi? 改進的Shishkin 網格上以及新混合差分格式在修正的Bakhvalov-Shishkin 網格上的誤差精度、收斂階數和收斂常數分別采用相應的公式計算。

表1 ε=10-10時2 種有限差分格式［3］在 Bakhvalov-Shishkin 和 Shishkin 網格上的數值結果Table 1 The numerical results of two schemes［3］ on the Bakhvalov-Shishkin and Shishkin meshes with ε=10-10

表2為中點迎風格式在Vulanovi? 改 進 的Shishkin 網格上的數值結果。表3 為新混合差分格式在修正的Bakhvalov-Shishkin 網格上的數值結果。定理 1 的式（10）得到證實。 對比表1～表3 中的數值結果知，新混合差分格式在修正的Bakhvalov-Shishkin 網格上邊界層 (x3N4，1]處得到的收斂階數和誤差精度要優于中點迎風格式在Bakhvalov-Shishkin 網格上、混合差分格式在Shishkin 網格上以及中點迎風格式在 Vulanovi? 改進的Shishkin 網格上的收斂階數和誤差精度。

表2 ε=10-10 時中點迎風格式在 Vulanovi? 改進的 Shishkin 網格［2］上的數值結果Table 2 The numerical results of the midpoint upwind scheme on theVulanovi?’s improved Shishkin mesh with ε=10-10

表3 ε=10-6 時新混合差分格式在修正的Bakhvalov-Shishkin 網格上的數值結果Table 3 The numerical results of the new hybrid scheme on the modified Bakhvalov-Shishkin mesh with ε=10-6

圖1 在修正的Bakhvalov-Shishkin 網格上新混合差分格式和3 種方法在區間[ xN 2，1]上的誤差Fig.1 The errors of the new hybrid scheme on the modified Bakhvalov-Shishkin mesh and other three methods on[ xN 2，1]

圖1 表明，新混合差分格式在修正的Bakhvalov-Shishkin 網格上邊界層處的誤差精度優于中點迎風格式在Bakhvalov-Shishkin 網格上、混合差分格式在Shishkin 網格上的誤差精度以及中點迎風格式在Vulanovi? 改進的Shishkin 網格上的誤差精度。實際上，在求解區間[0，1]，新混合差分格式的最大誤差均較其他3 種方法小。

例2考慮奇異攝動問題：

其中，

數值結果見表4。

表4 中的數值結果同樣證實定理1 正確。

表4 ε=10-10 時新混合差分格式在修正的Bakhvalov-Shishkin 網格上的數值結果Table 4 The numerical results of the new hybrid scheme on the modified Bakhvalov-Shishkin mesh with ε=10-10

4 結 論

證明了奇異攝動問題的最大值原理，并研究了混合差分格式在修正的Bakhvalov-Shishkin 網格上求解一般奇異攝動問題。在邊界層(x3N4，1]處，此方法取得二階收斂，其誤差精度均好于中點迎風格式在Bakhvalov-Shishkin 網格上、混合差分格式在Shishkin 網格上以及中點迎風格式在 Vulanovi? 改進的Shishkin 網格上的誤差精度。盡管此方法整體上仍為一階，但因在邊界層達到了二階收斂，因此，實際上取得了較好的整體誤差精度。