基于消費者損失效用的概率銷售策略研究
楊 光,劉新旺,秦晉棟
(1.南京信息工程大學管理工程學院, 江蘇 南京 210044;2.東南大學經濟管理學院,江蘇 南京 211189;3.武漢理工大學管理學院,湖北 武漢 430070)
1 引言
近年來隨著互聯網支付平臺的興起,消費者的消費方式發生了巨大的變化,現代市場行情變得更為錯綜復雜,市場競爭異常激烈,任何企業要想成功進入、占領、鞏固和擴展市場,采用正確的營銷策略顯得尤為重要。一般來講,銷售商可供選擇的市場營銷策略包括產品策略、價格策略、促銷策略和渠道策略等等[1],其中促銷策略最為常見,促銷手段主要有折扣、返現、抽獎以及免費體驗等方式,促銷形式包括廣告宣傳、公共關系、促銷活動、人員銷售、口碑操作等,而概率銷售作為促銷策略中比較新穎的策略越來越被人們所熟知。2008年Fay和Xie首次提出了概率產品(簡稱PG)(Probabilistic Goods)和概率銷售 (Probabilistic Selling)(簡稱PS)的概念[2],概率銷售作為一種新型銷售模式與其他銷售方式相比有其獨具的特點和明顯的優勢,能夠達到擴大市場、細分市場、差異化定價、弱化市場不確定確定影響、平衡供求、增加資源利用效率等效果[2]。
關于概率銷售領域的早期文獻主要關注壟斷與競爭[2-5],需求不確定[2,5]等主題。最近的概率銷售文獻主要關注以下幾個主題,一是將庫存管理理論用于概率銷售策略的研究[6-9],Fay和Xie[7]研究了產品時間分配對概率商品消費者的影響。PS作為一個庫存管理機制既能提高銷售商或廠商利潤又能增加社會福利; 二是與概率銷售策略相似策略的比較分析[10-12],Chen等[11]考慮一個兩階段模型來研究報價(PP)與自己標價(NYOP)兩種不同銷售機制的影響。三是將博弈方法及動態規劃等用于概率銷售的研究[9,13],Xiao Yongbo和Chen Jian[9]用連續時間離散狀態有限期限動態規劃模型,研究了兩種場景下的最優決策,其價值函數可以作為基準來評估概率銷售(PS)關于需求的誘導效應和稀釋效應;Cai Gangshu等[13]利用靜態博弈研究兩個供應商和一個銷售商如何使用概率銷售和渠道選擇問題;Rice等[12]模型將概率銷售與削價銷售策略進行了比較分析,模型顯示概率銷售與削價銷售相比具有提高邊際收益和庫存利用率等優勢。
與概率銷售密切相關的主題是考慮消費者理性對概率銷售的影響[14], 以及銷售商如何利用產品屬性差異來創造概率產品[2,7-8]及在競爭市場下概率銷售策略的實踐應用[4-5,15],Fay等[10]研究表明概率銷售影響零售商實施概率產品的類型和數量,采用PS策略可以改變最優產品的數量,還可以作為新產品的替代或補充。Huang Tingliang和Yu Yimin[14]研究表明概率銷售在有限理性條件下最優,可以減少廠商間的價格競爭及增加產業利潤,研究指出人們低估了概率銷售對有限理性消費者的作用。值得一提的是很少有研究者利用不同質量產品來構造概率產品。Zhang等[8]研究不同質量市場下的概率銷售策略,研究發現如果銷售商產能過剩則銷售商在不同質量市場下采取概率銷售是有利可圖的。
上述文獻沒有考慮消費者的損失偏好,由于消費者的需求個性越來越分散化,許多文獻關注消費者的損失厭惡或損失規避。Zhao和Stecke[16]考慮了消費者的損失厭惡對提前訂購策略的影響并研究了銷售商提前銷售的利益最大化問題。Abdellaoui等[17]提出多種損失厭惡的概念并證明多數個體存在損失厭惡。Blavatskyy[18]將損失規避的概念擴展為更一般的情形,即損失規避的結果不是用錢去度量,研究表明人們可能會傾向于模糊偏好來代替博彩。借鑒前景理論中的參考點依賴和風險損失規避效應,Won[19]分析了消費者的損失厭惡對經驗優勢的影響。Kim和Lee[20]介紹了在消費者損失厭惡下的銷售商利益最大化行為決策,并討論了損失厭惡在價格歧視和產品差異中的實踐應用。Wang和Webster[21]將損失厭惡引入報童模型中考慮單周期的報童決策問題,研究發現在損失厭惡條件下如果不存在缺貨成本,報童的訂購量會多于風險中性條件下的訂貨量。將消費者分為損失中立型和損失厭惡型,Ma Shanshan等[22]考慮實體渠道和網絡渠道兩種銷售渠道,研究了銷售商是否應該參與網上渠道銷售,并檢驗了消費者的需求均值對銷售者策略的影響。最近,杜文意等[23]在損失厭惡型零售商存在資金短缺的現實情形下,研究了基于融資需求的損失厭惡型零售商訂貨策略問題,王良等[24]對靜態線性損失厭惡下的最優資產配置策略模型及其性質進行了分析,構建了基于TGARCH-EVTPOT-GPD的動態市場風險測度方法,提出了時變損失厭惡條件下基于動態條件風險約束的ETF基金最優資產配置策略模型。
雖然上述文獻主要關注不同情境下的概率銷售策略,但大多研究者忽視了消費者在購買概率產品后會產生潛在損失。概率產品被認為是一種“隨機產品”,只有在購買后產品的信息才會被披露,若消費者購買后的概率產品是低質量產品,則消費者不準退貨,這被稱為“不返還”策略。在實際的銷售實踐中存在以下兩種可能購買后悔損失情形:(1)消費者不應該購買任何產品;(2)消費者應該購買最偏愛的透明產品。第一種被認為是“購買損失”,第二種被認為是“選擇損失”。
本文主要的創新點體現在以下幾個方面:一是我們構建了概率銷售在損失中性和損失厭惡下異質產品的概率銷售模型并探討期望損失對概率銷售策略的影響和作用。二是我們模型納入了異質產品市場下的概率銷售的一些重要特征,工業實踐表明生產高質量產品的廠商一般不會采用概率銷售策略,因為銷售價格打折的概率產品會讓他們名譽受損。
三是我們首次將期望損失納入概率銷售模型中,研究表明消費者的期望損失能否激發銷售商采用概率銷售策略主要取決于消費者對購買損失和選擇損失敏感度。“購買損失”會使得概率產品的感知質量與質量正相關,而“選擇損失”則會讓感知質量與質量負相關,我們把后者稱為“反質量歧視”。當消費者對“選擇損失”更敏感時,則概率銷售的零售商會利用“反質量歧視”,此時對于高端消費者來說,期望損失會在更大程度上降低概率產品的感知質量,這種“反質量歧視”可以增加消費者對產品的感知差異,并保持概率產品對兩端消費者的吸引力。
最后我們比較銷售商在損失中性和損失厭惡下的概率銷售策略變化和對收益的影響,同時驗證了異質產品市場下 “反質量歧視”效應和實施概率銷售中的“不返還”策略,這些機制可以擴大產品間的質量差異,同時讓銷售商獲取更多利潤。
2 基于損失效用的概率銷售模型
2.1 問題描述
2008年Fay和Xie[2]首次提出了概率產品和概率銷售的概念,概率產品并不是一個具體的產品, 而是指銷售商通過概率的指定在一系列銷售的產品中創造出的虛擬產品。概率銷售是指一種銷售策略,即銷售者利用其現有的產品或服務來創造概率產品,并把概率產品作為對潛在購買者的一種附加購買選擇。例如一般國外消費者愿意從網站Hotwire.com或Priceline.com購買帶折扣的酒店,而帶折扣酒店的信息在消費者購買后才被披露,這種銷售商銷售策略即為概率銷售策略,這種產品為不透明產品或概率產品,而傳統實體銷售的產品在后文中稱為透明產品,再例如銷售商在傳統銷售模式下以原價銷售兩種產品A和B,而概率銷售模式則以折扣價格銷售概率產品(PG),此時產品類型只有在購買后才能被披露,具體銷售模式見圖1所示。
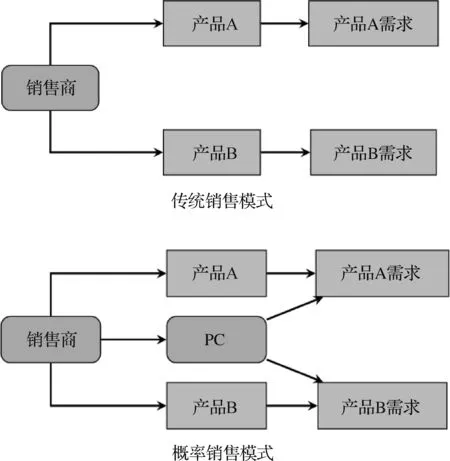
圖1 傳統銷售與概率銷售對比圖
2.2 假設說明
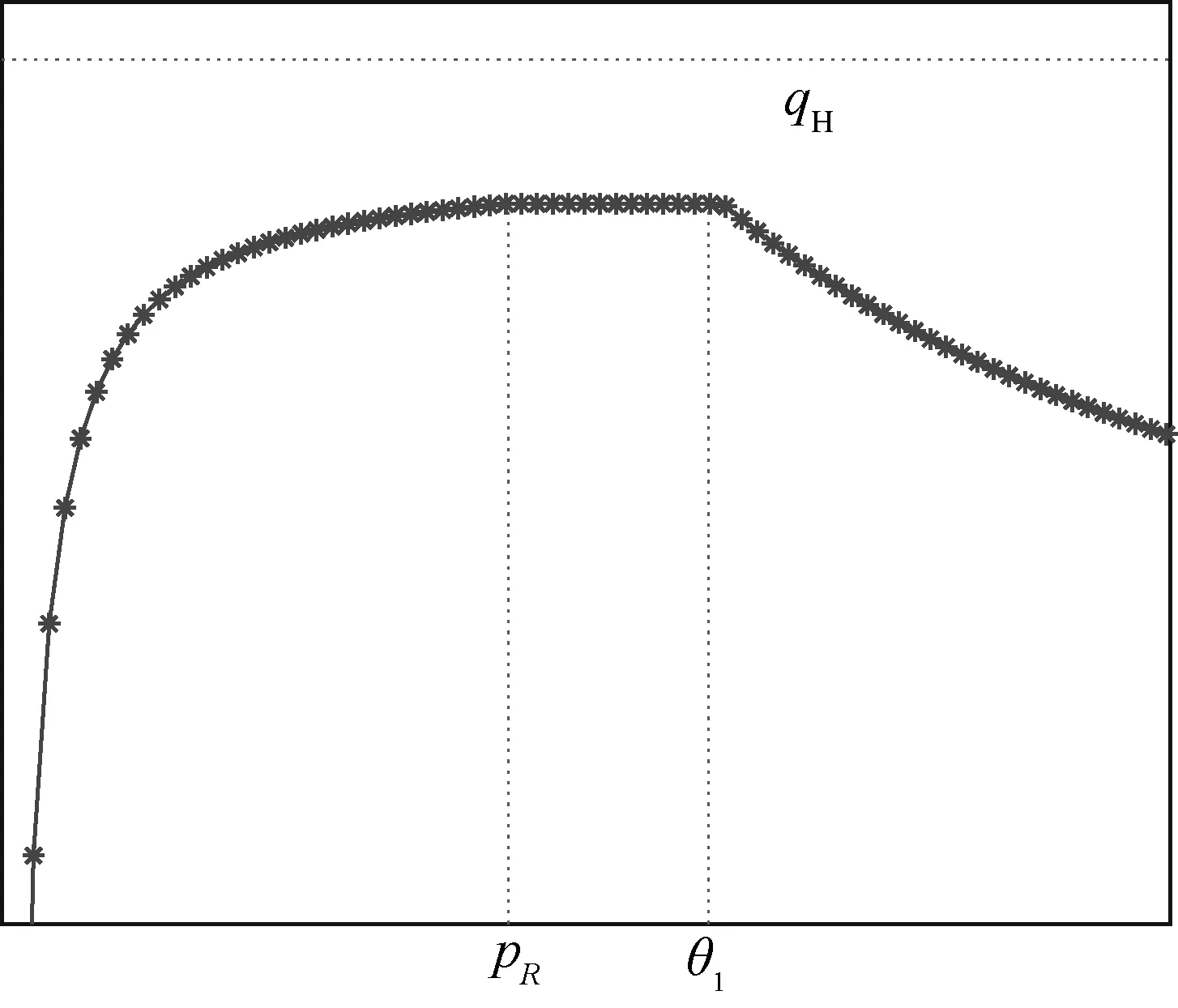
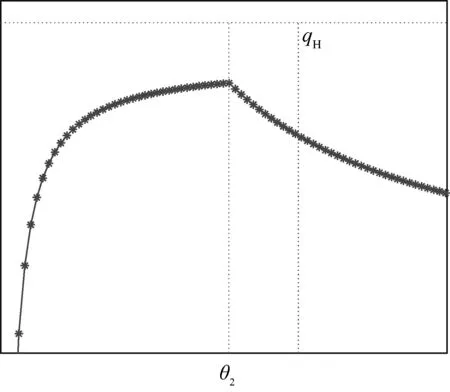
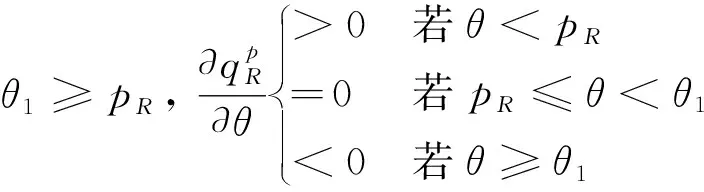
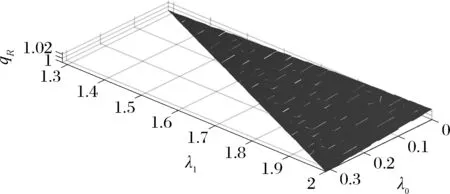
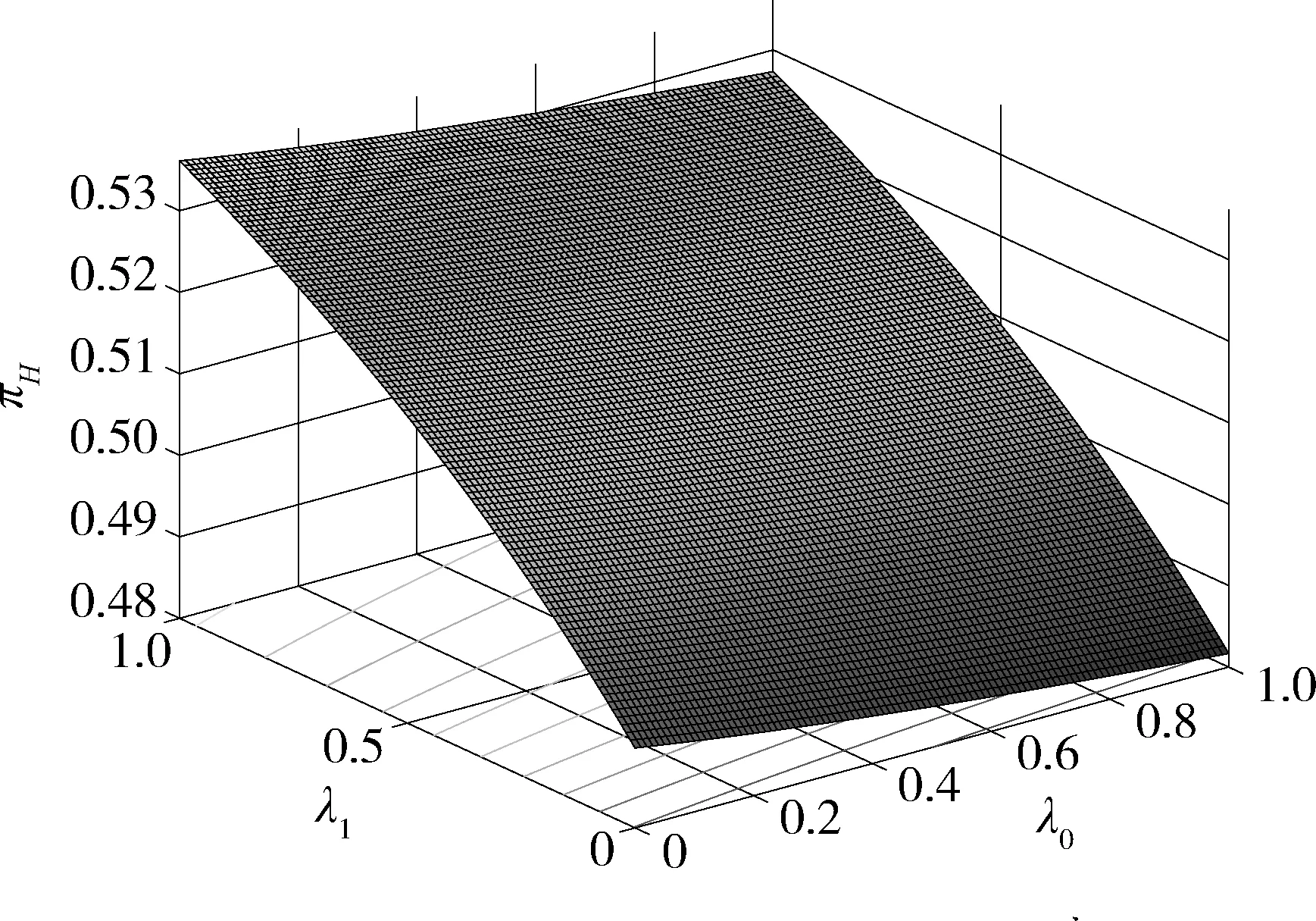
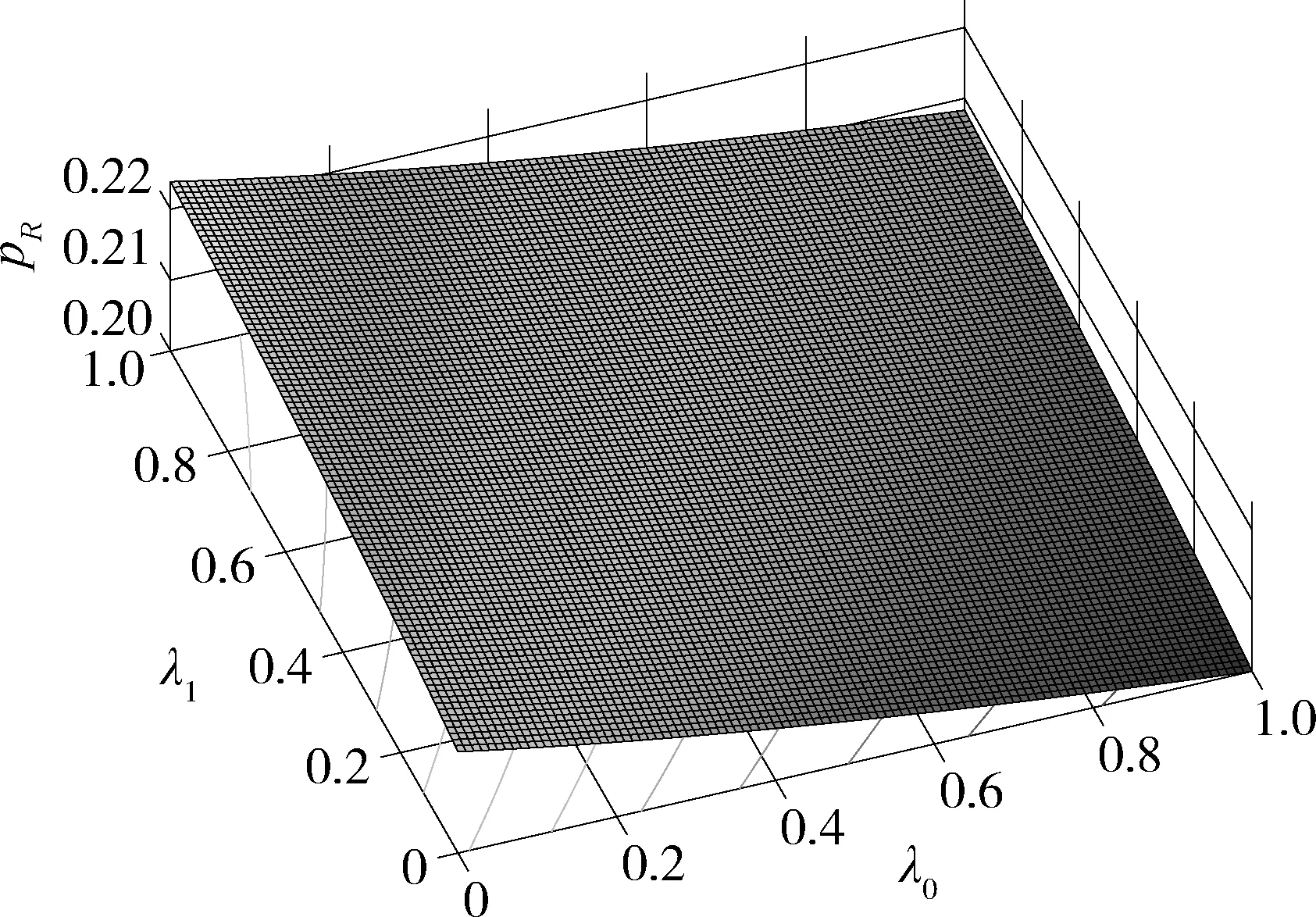
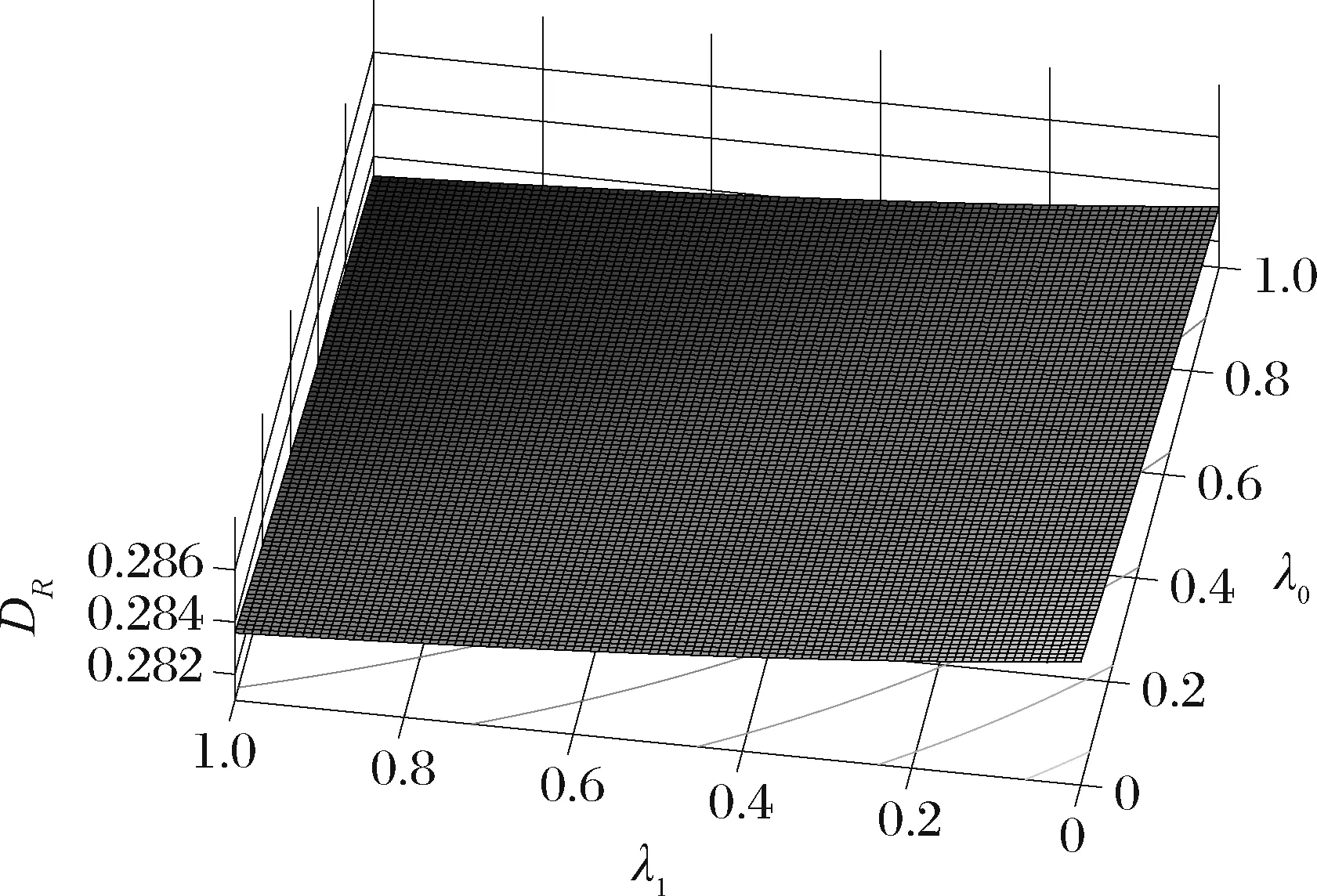
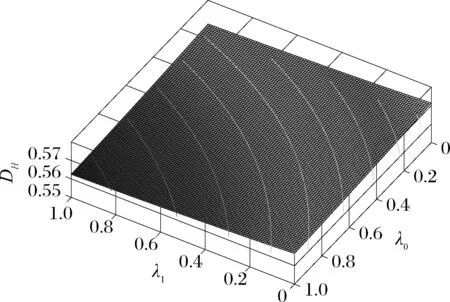
假設整個市場有兩個銷售商,銷售商H和銷售商R,每個銷售商僅銷售單位產品,銷售商H提供質量等級為qH的透明產品,而銷售商R提供三種不同產品,第一種是質量為qM的透明產品M,第二種是質量為qL的透明產品L,第三種是由產品M和產品L混合的概率產品R,消費者自主選擇產品而購買產品的質量等級則隨機產生,購買到產品的質量等級只有兩種qM或qL,其中qL< 假設市場中存在大量單位需求消費者,每個消費者只購買一個產品,考慮本文模型計算的復雜性假設消費者的質量偏好服從均勻分布,即θ~U(0,1),質量偏好為θ的消費者在損失中性下以價格為pi購買產品i(i=H,M,L)的效用為u=θqi-pi(i=H,M,L,R)。 定義不同損失偏好下消費者的效用[16]為, u 上述效用區分了損失中性消費者和損失厭惡型消費者,消費者購買透明產品不存在損失,因為消費者購買透明產品不存在不確定性,而購買概率產品,由于產品質量的不確定性導致消費者購買后損失。下節將分別討論損失中性和損失厭惡下的概率銷售模型。 為了便于與損失厭惡下的概率銷售模型相比較,首先我們研究在損失中性下的概率銷售模型,將損失中性概率銷售模型作為基準模型,采用逆向演繹方法,從最后一階段消費者選擇產品開始分析,給定價格和質量水平(pi,qi)(i=R,H),我們得到不同消費者偏好對質量的臨界點:第一個臨界點是消費者買概率產品和不買產品無差異,第二個臨界點是消費者買產品H和買產品R無差異,上述兩個臨界點如下: (1) 銷售商R和銷售商H的需求分別為(θR-θ0)和(1-θR),因而銷售商H和銷售商R的利潤分別為 πR=pR(θR-θ0),πH=pH(1-θR) (2) 根據式(2)可以求出均衡價格和質量,在第一階段銷售商R在區間[1,qM]上選擇最優質量,得到下面損失中性下的性質: 引理1 如果消費者購買概率產品R中獲得產品M沒有損失,則應滿足下列條件: θqM-pR≥max{0,θqH-pH} 證明:見附錄引理1的證明。 在引理1的基礎上我們得到下列損失中性下的結論。 定理1(損失中性)在損失中性下有下列結論: 證明:見附錄定理1的證明。 本節首先定義期望損失和感知質量,類似損失中性情況,我們建立基于損失厭惡下的概率銷售模型,進而得到一些性質。 定義1 期望損失 (3) 其中λi(i=0,1)分別表示消費者買產品和不購買產品H兩種類型損失厭惡下的損失厭惡系數,[x]+=max{0,x}。 由上述定義1說明當消費者購買概率產品買到產品L時會損失厭惡,這是消費者理性選擇的結果,當消費者購買概率產品后得知是產品M不會損失厭惡,因為消費者在購買前清楚購買概率產品的最好結果就是買到產品M, 期望損失分為存在下列兩種類型: (1)購買行為本身的損失(不買與買到低質量產品作比較),比如消費者購買概率產品買到低質量產品,則消費者可能會想如果不買概率產品則不會有損失,此種類型被認為“購買損失”。 (2)不購買透明產品帶來的損失(買透明H產品與買到低質量產品作比較),例如購買概率產品買到低質量產品,消費者可能會想如果去選擇透明產品則不會有損失,此種類型被認為“選擇損失”。 定義1考慮上述兩種類型的損失厭惡,其中λ0是類型(1)的損失厭惡系數,λ1是表示類型(2)的損失厭惡系數,這兩個類型的損失厭惡系數在后文中將起到關鍵的作用。 根據式(3),期望損失的第一項為正當且僅當θ (4) 當然可能存在θ1 (5) 我們定義概率產品的感知質量: 定義2 感知質量 根據感知質量的定義,則存在下列兩種情形: 圖2 當θ1≥pR時感知質量的倒U形曲線 圖3 當θ1 引理2 消費者的對產品R的感知質量是呈倒U/V型,存在下列兩種情形: 其中θ1和θ2分別如式(2)和(4)所示。 (6) 當消費者購買概率產品和買高質量產品無差異的質量臨界點由 (7) 引理3 消費者分類(損失中性) 質量偏好位于區間θ∈[θ0,θR]上的消費者會選擇概率銷售產品R,質量偏好位于區間θ∈[θR,1]上的消費者會選擇產品H,θ0和θR如式(1)所示。 引理4 消費者分類(損失厭惡) 質量偏好位于區間θ∈[?0,?R]上的消費者會選擇概率銷售產品R,質量偏好位于區間θ∈[?R,1]上的消費者會選擇產品H,?0和?R分別如式(6)和(7)所示。引理4說明當消費者對質量要求比較高θ∈[?R,1]時,會選擇產品H,當消費者對產品的要求比較適中θ∈[?0,?R]時,會選擇概率產品,當消費者對質量要求比較低θ∈[0,?0]時離開市場不購買任何產品。 由引理4知,在損失厭惡下銷售商R和銷售商H的利潤分別為 銷售商R選擇pR最大化其利潤,銷售商H先擇pH最大化其利潤,解得最優的價格,最優價格均是qR和qM的函數,銷售商R再選擇最優的qM,得到下列定理2歸納的均衡結果: 定理2(損失厭惡) 在損失厭惡下有下列結論: (3)γ1(λ1)和γ2(λ1)均是關于λ1的遞增函數,銷售商R的最優利潤與損失中性最優利潤相比有下列特點: 證明:見附錄定理2的證明。 定理2說明以下問題,第一,當存在損失厭惡的情況下,只要λ0足夠小(與λ1相比),λ0小于特定的閥值時λ0是關于λ1的遞增函數,此時銷售商R提供概率產品,事實上若消費者在購買概率產品后有損失,則概率銷售策略此時不具有吸引力,致使消費者不愿意購買概率產品,但下面的情形則消費者愿意購買概率產品,當λ1>λ0時,存在下列幾種情況,第一種情況λ0≤γ1(λ1),與定理1中的情況(1)不同,此時銷售商總是采用概率銷售策略,第二種情況與定理1中的情況(2)相同,當γ2(λ1)≥λ1≥λ0時銷售商也總是采用概率銷售策略,與定理1相比在λ1>λ0時銷售商R似乎更愿意采用概率銷售策略;而相反在λ1≤λ0時也存在下列三種情況,第一種情況γ1(λ1)≤λ1≤λ0時,銷售商R不采用概率銷售策略,這與定理1的情況(1)相同,第二種情況與定理1的情況(2)類似,只有當λ0≤γ2(λ1)時銷售商才開始采用概率銷售策略,與定理1相比,銷售商R在λ1≤λ0時不太傾向使用概率銷售策略。 第二,當且僅當消費者買產品H的損失厭惡系數比不買產品H的損失厭惡系數小時(例如λ1≥λ0),銷售商R的利潤比在損失中性下利潤高,由引理2知消費者的感知質量呈倒U/V形,因此使用概率銷售策略會更容易讓分布在兩端的消費者受損失,即對質量要求低的消費者會因為購買產品H而損失,而對質量要求高的消費者會因為不購買產品H而損失,前者的損失受厭惡系數λ0影響,而后者則受厭惡系數λ1影響,λ0作為購買損失類型(1)的度量,消費者也是通過λ0來感知產品質量的,隨著消費者對質量的要求越來越高,對產品質量的感知能力也越來越強,若消費者感知到產品質量越來越差時,則此時消費者便不愿意購買,這就迫使銷售商為了留住消費者而降價進而導致銷售商利潤降低;λ1作為損失類型(2)的一種度量,隨著消費者對質量要求越來越低,對產品質量的感知能力也逐漸降低,我們稱這種規律為“反質量歧視”,兩銷售商對高端消費者(θ∈[max(θ1,θ2),1])的爭奪競爭激烈,消費者對概率產品的感知質量的削弱會增大概率產品和透明產品之間的差異,這就致使銷售商增大質量差異定更高的價格,進而使得概率銷售商獲取更高的利潤,具有損失厭惡的概率銷售和損失中性的概率銷售的利潤誰高誰低取決于兩種損失厭惡類型消費者的期望損失敏感性的強弱。 定義 其中γ1(λ1)和γ2(λ1)的表達式見附錄定理2的證明。 從定理2知當固定λ1不變時,隨著λ0增加到閥值γ1(λ1)時,銷售商R停止概率銷售。下面討論當固定λ0不變時,隨著λ1增加會出現什么規律?下面的推論給出了回答。 推論2 (極限性質)γ(λ1)關于λ1遞增,對任意的λ0≥0,存在反函數 若λ1≤γ-1(λ0),則銷售商只銷售透明產品,否則銷售商R只銷售概率產品。另外,存在下列極限性質: 證明:見附錄推論2的證明。 推論2說明保持λ0不變,即使損失厭惡系數λ1趨向無窮大,銷售商R仍然銷售概率產品,這是因為實施“反質量歧視”的唯一方法就是采用概率銷售,隨著λ1的逐漸增大,銷售商會降低產品L在概率產品中的比例,但這個比例不會降到0,這就意味著消費者在買概率產品時買到產品L的幾率會降低,在存在市場競爭下銷售概率產品可以降低消費者對產品的感知質量,換句話說銷售概率產品可以有效降低兩銷售商之間的競爭,因為競爭情形下當產品的質量差異不大時消費者會夸大市場中的產品的感知質量差異。 本節主要探討參數對不同損失情形下最優收益、最優質量、價格及需求的影響,由定理2知銷售商R的利潤函數關于λ1遞增,關于λ0遞減,下面我們進一步研究參數λ1和λ0對產品R的期望質量的影響,固定qM和λ1不變,增加λ1會減少低端消費者對概率產品R的需求,因此銷售商R必須降低價格增大qM,這會加劇銷售商R和銷售商H之間的競爭,兩個銷售商的利潤均會降低。 首先固定qH,qM研究qM和λ0及λ1的關系,圖4和圖5分別是當qH=3,qM=2及qH=1.5,qM=1.2時銷售商R的qM和λ0及λ1的關系圖,由圖4和圖5知當λ0≥γ(λ1)時,銷售商R不會銷售概率產品,故隨著λ0的增大,qM增加到qM或者降低到qL,主要取決于利潤大的產品。 圖4 qR與λ關系當qH=3, qM=2 圖5 qR與λ關系當qH=1.5, qM=1.2 下面我們研究銷售商R及H隨著參數λ1和λ0的變化關系,下列推論3揭示他們之間的關系。 推論3 固定λ1,銷售商R和銷售商H的價格、需求以及利潤均是關于λ0的遞減函數;固定λ0,銷售商R和銷售商H的價格、需求以及利潤均是關于λ1的遞增函數。 證明:見附錄推論3的證明。 推論3說明固定λ1,則銷售商R和銷售商H的收益均隨著λ0的增大而遞減,下面我們結合圖6-10來說明,具體參數設置如下qH=3,qM=2,qR=1.5,圖6說明銷售商R的利潤隨著λ0的增大而遞減,隨著λ1的增大而遞增,圖7說明銷售商H利潤表現出同樣的規律,即隨著λ0的增大而遞減,隨著λ1的增大而遞增。固定qH=3,qM=2,圖8說明銷售商R的定價隨著λ0的增大而遞減,隨著λ1的增大而遞增,同理圖9是銷售商H的定價隨厭惡系數(λ0,λ1)的變化關系,圖9說明銷售商H的最優價格關于λ0遞減而關于λ1遞增,與銷售商R的定價(圖8所示)相比銷售商H的定價隨著λ0遞減得更快,其中銷售商R的定價隨著λ1直線增長,而銷售商H的定價隨著λ1曲線增長,圖10和圖11是銷售商R和H的需求隨著厭惡系數(λ0,λ1)的變化關系,圖10和圖11說明銷售商R和H的需求均關于λ0遞減而關于λ1遞增,同時銷售商H的需求是銷售商R需求的兩倍。 圖6 銷售商R的利潤隨λ0和λ1的變化關系 圖7 銷售商H的利潤隨λ0和λ1的變化關系 圖8 pR 隨λ0和λ1的變化關系 圖10 DR 隨λ0和λ1的變化關系 圖11 DH隨λ0和λ1的變化關系 本文首先構建了損失中性下異質產品的概率銷售模型,以此為基礎建立了損失厭惡下異質產品的概率銷售模型,研究了不同損失類型消費者對異質產品概率銷售策略的影響,最后討論了相關參數對銷售商的收益、定價、最優質量的影響。 概率銷售作為一種新型的銷售模式,本文主要解決了在銷售期限內如何控制概率銷售中產品質量差異問題,消費者的損失偏好如何影響收益、定價和需求的問題,銷售商在面對不同類型損失的消費者,控制產品的質量,將概率銷售和普通銷售有機結合起來,對于高檔產品的銷售商主要采用普通銷售,主要吸引高端消費者,擴大產品的差異化程度實行差異化定價;對于中低檔產品的銷售商采用概率銷售和普通銷售相結合的策略,當產品的質量適中時采用概率銷售,當產品的質量差異位于兩端時則采用普通銷售,在具體銷售實踐中將概率銷售和普通銷售靈活統一起來,根據消費者的損失偏好靈活控制產品差異,實現最大化收益。對于不同損失偏好的消費者來說,增強對產品質量的感知能力,判斷產品的質量,根據自己的判斷選擇不同的銷售商,若消費者對產品的質量要求高,則選擇高端產品的銷售商;若消費者對產品的質量要求適中,則選擇概率銷售的銷售商,消費者首先應理性判斷產品質量,同時兼顧自身的經濟狀況選擇合適的銷售商及產品。銷售商提供概率銷售策略為消費者買到物美價廉的產品提供了一種可能。2.3 損失中性下的概率銷售模型
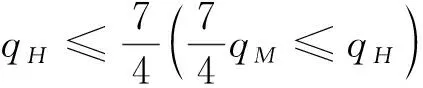
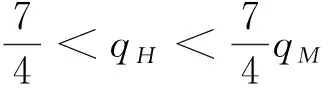
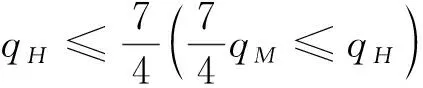
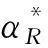
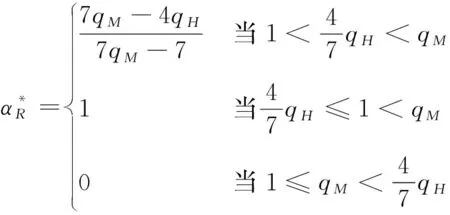
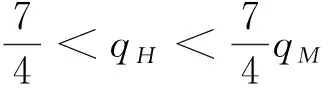
2.4 基于損失厭惡的概率銷售模型
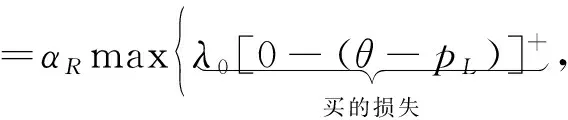
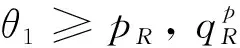
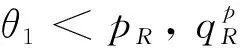
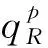
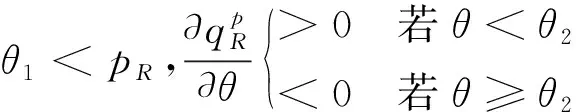
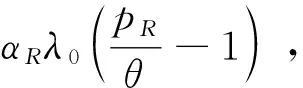
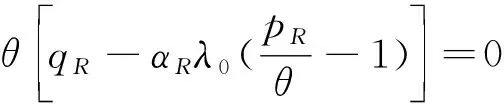
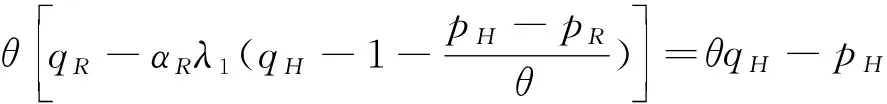
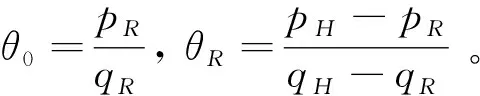
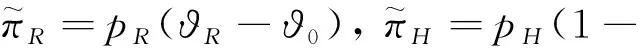
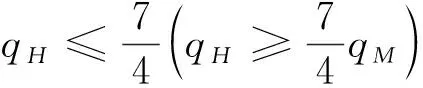
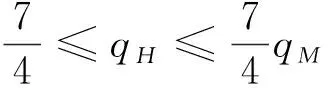
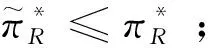
3 數值分析
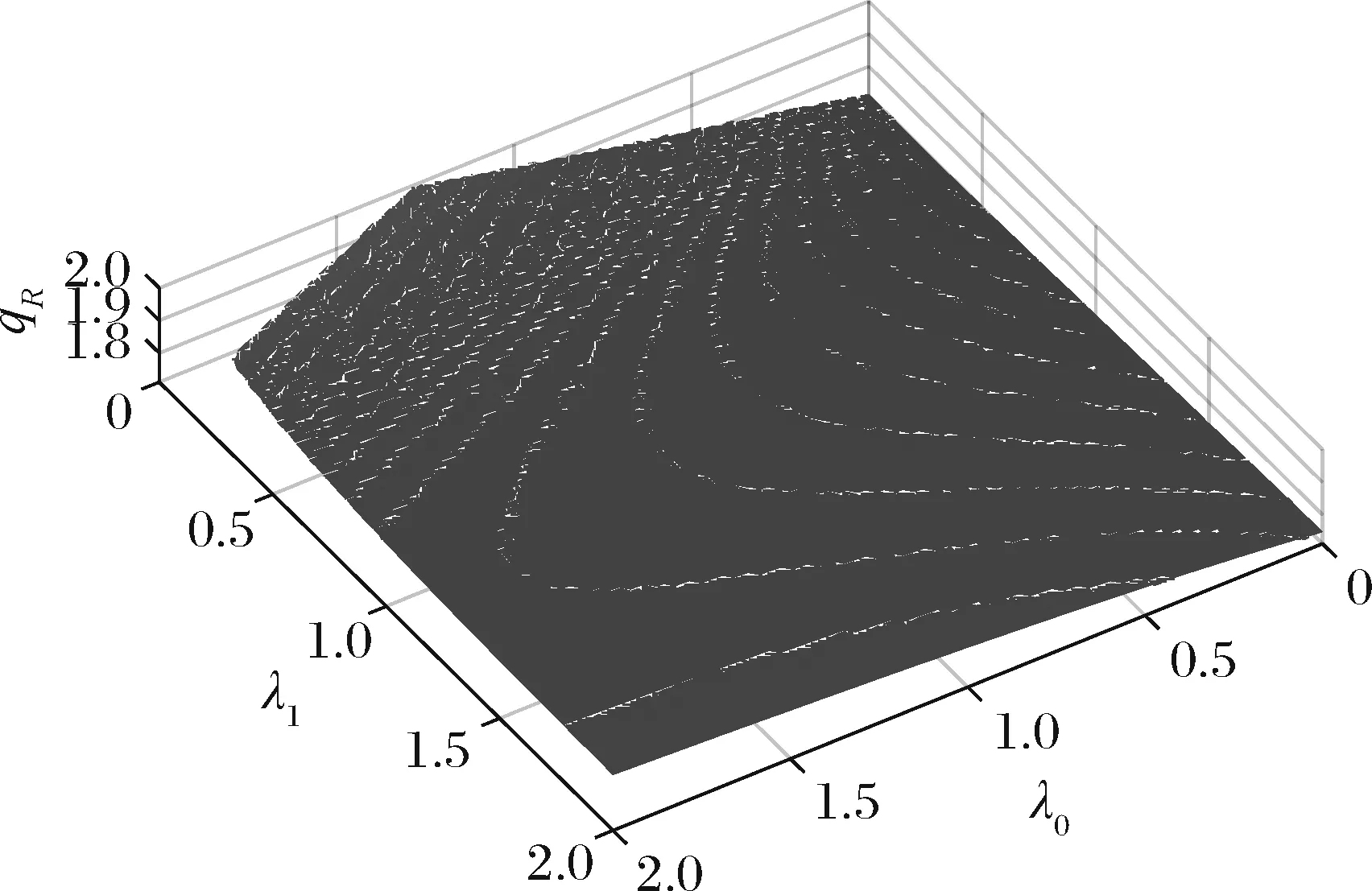

4 結語

