基于“相互作用論”的課堂活動單的設計

摘 要：學生的數學邏輯思維的能力不是天生就有的，而是學生這個主體作用于客體后產生的。因此，在課堂教學活動中，教師既要體現學生的主體性，又不能忽視客體的作用，而課堂活動單能將兩者有機結合起來。

關鍵詞：“相互作用論”;課堂活動單;同化;順應

中圖分類號：G421? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? 文章編號：2095-624X（2020）24-0043-02

引 言

課堂活動是教師在課堂上組織學生參與學習、調動學生親身體驗學習、引導學生合作學習、發揮學生主觀能動性的一個很好的載體。知識的學習絕對不是簡單的操作與模仿，思維能力必須通過學生的親身參與才能獲得發展。

一、皮亞杰“相互作用論”

皮亞杰的“相互作用論”簡單來說，就是學生的思維發展不是主體和客體的單一作用產生的，而是主體與客體的相互作用產生的結果。那么學生為什么要發展思維呢？學生的行為和思維的目的又是什么呢？皮亞杰認為，學生的行為和思維的目的都是能夠以更好的方式來適應外部環境。適應是學生不斷地運用和修改對外界世界的內部表達的過程，也是學生的認知結構不斷發生變化的過程，更是學生越來越準確地表達外部世界的過程[1]。

二、“相對作用論”對課堂活動單設計的作用

課堂活動單是教師依據《義務教育數學課程標準（2011年版）》和學生學情，把教材內容與要求以及相關教學資源轉化為具有目標性、整體性、層次性、建構性和可操作性的學生活動方案。它有別于教案和學案，更不是練習紙。由于課堂活動單的使用者是學生，課堂活動單必須符合學生的認知發展與心理發展特點，依據學生的立場設計與表述，重視學什么和怎么學[2]。

三、“7.1探索直線平行的條件（2）”課堂活動單設計案例研究

1.基于原有認知結構創設情境

皮亞杰認為，知識是作為學生行為世界的結果被構建的。因此，知識的結構對學生的認知起著橋梁的作用，從較為簡單的結構到更為復雜的結構，在這個不斷完善的過程中，知識變得越來越豐富。而這個過程完全依賴于學生活動，可以說，學生活動是學生學習的“根”，因此知識的學習應該植根于活動情境中。基于現實原因，初中數學的學習不可能每天離開課堂去開展社會實踐活動，但是教師可以注重創設與實際生活有關的情境，并以學生為中心開展活動[3]。

片段一：創設情境，引入課題

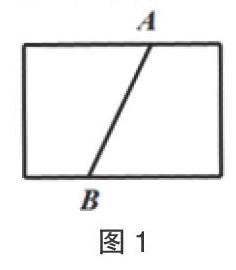
在一塊小紙板上畫線段AB（見圖1），如何通過度量圖中某些角的大小來判斷木板的上、下邊緣是否平行？

（1）獨立思考完成問題。

（2）小組內交流。

①你們小組選用哪些角？

②這些角在數量上存在怎樣的關系？

（3）小組展示，其他組補充。

【設計意圖】從實際生活出發，從感性的角度認識到“內錯角相等，兩直線平行”“同旁內角互補，兩直線平行”，為下面的教學做鋪墊[4]。

2.以學生為中心加強同化

同化是把外界元素整合在一個集體的正在形成或已經形成的過程。課堂教學必須適合學生的認知結構，教學內容只有符合或接近學生的認知結構，才能引起學生積極的學習活動，才能使教學內容有效地被學生同化。簡單來說，教師應站在學生的立場上去設計課堂活動單，讓活動內容能激發學生的學習興趣[5]。

片段二：探索交流

問題1：（見圖2）直線a、b被直線c所截，∠2=∠3，直a與直線b平行嗎？為什么？

（1）獨立思考完成問題。

（2）小組內交流。

①你們用哪對角的關系來說明直線a與直線b平行？理由是什么？

②在解決這個問題的過程中，你們采用了什么方法？

（3）小組展示方法。

問題2：（見圖3）直線a、b被直線c所截，∠2+∠3=180°，直線a與直b平行嗎？為什么？

（1）獨立思考完成問題。

（2）小組內交流。

①你們用哪對角的關系來說明直線a與直線b平行？理由是什么？

②在解決這個問題的過程中，你們采用了什么思想方法？

（3）小組展示方法。

【設計意圖】讓學生體會當遇到一個新問題時，可把它轉化為已知的問題來解決[6]。

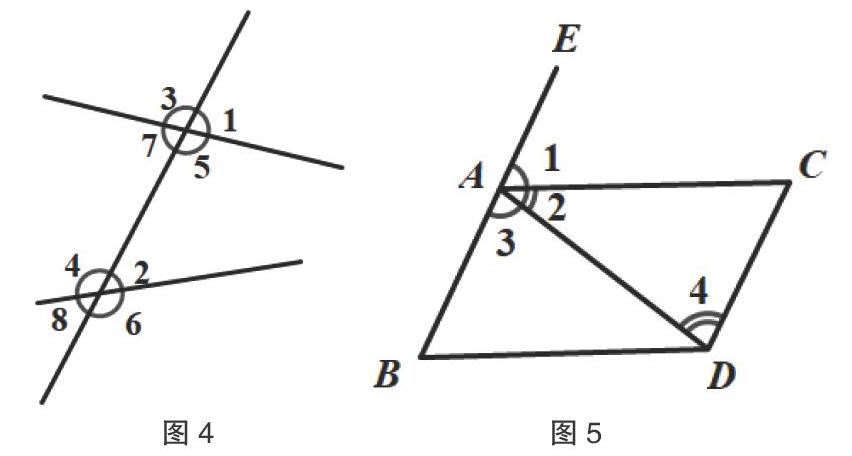
問題3：在兩條直線a、b被直線c所截而成的8個角中，像∠2與∠7這樣的一對角稱為內錯角，像∠2與∠5這樣的一對角稱為同旁內角（見圖4）。

（1）小組交流

①圖中還有其他的內錯角或同旁內角嗎？

②如圖5所示，∠1與∠3、∠3與∠4、∠2與∠4分別是哪兩條直線被哪一條直線截成的？它們分別是什么角？

（2）歸納總結：除了“同位角相等，兩直線平行”這個基本事實，我們又得到了：

①文字語言：________________________________

幾何符號語言：________________________________

②文字語言：________________________________

幾何符號語言：________________________________

【設計意圖】通過觀察、比較，認識“內錯角”“同旁內角”，歸納兩條直線平行的條件。

3.加深學生認知結構，促進順應

順應是學生由于學習過程中不能順利同化新知識而對認知結構做出的調整，包括對錯誤認知結構的糾正和正確認知結構的進一步拓寬和加深，從而使認知結構發生質的變化[7]。在課堂活動單的設計中，教師要充分利用學生原有的認知結構，讓其發揮同化作用，同時也要適當的設計一些超出學生原有認知結構但又在學生最近發展區內的活動，促進學生認知結構升級。

片段三：思路點撥

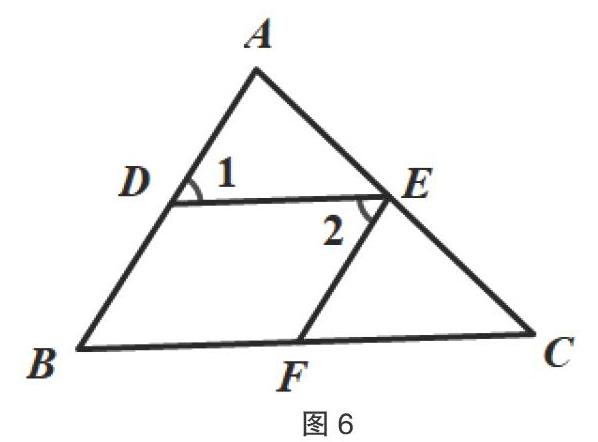
問題4：如圖6所示，∠1=∠2，∠B+∠BDE=180°。指出圖中相互平行的直線，并說明理由。

（1）獨立思考完成問題。

（2）小組交流。

①圖中互相平行的直線有哪些，為什么？

②在解決問題的過程中，你們用到了什么方法？

（3）小組展示解題方法。

變式：如圖7所示，∠1∶∠2∶∠3=2∶3∶4，∠ADE=60°，∠BFE=120°。指出圖中相互平行的直線，并說明理由。

（1）獨立思考完成問題。

（2）小組交流。

①圖中互相平行的直線有哪些，為什么？

②在解決問題的過程中，你們用到了什么方法？

（3）小組展示本組的錯誤之處。

（4）小組交流解題思路：

________________________________________________________________

________________________________________________________________

【設計意圖】讓學生在合作交流的過程中，明確說明兩直線平行的一般思路。

結 語

杜賓斯基說過：“數學是困難的，不管用什么教學方式都無法改變這個事實。所以，學生在數學的學習上，必須始終保持一種欣賞的心態，只有這樣才能逐漸發現數學的美。”因此，教師設計好一份課堂活動單尤為重要。它能更好地組織學生學習、發展學生的思維。

[參考文獻]

劉金花.兒童發展心理學（第三版）[M].上海：華東師范大學出版社，2013.

章建躍.中學數學課程教材的思考[J].課程·教材·教法，2007（10）：42.

科軍.初中數學高效課堂教學模式構建初探[J].學周刊，2020（22）：19-20.

王琦.提高初中數學教學課堂效率的措施探究[J].學周刊，2020（20）：68-69.

龐錕.優化課堂，激發學習——探討新課改下初中數學有效性教學[J].學周刊，2020（20）：111-112.

宋兆英.初中數學課堂教學模式探究[J].學周刊，2020（19）：23-24.

黃菁菁.初中數學課堂教學設計的精確性探討[J].當代教研論叢，2020（06）：74.

作者簡介：全麗潔（1981.11—），女，江蘇太倉人，太倉市浮橋中學校長助理，一級教師。