完整井抽降水引起的側向有界越流承壓含水層變形解析研究

蔡兵華，李忠超 ，馮慶高，袁 祥

(1.武漢市市政建設集團有限公司，湖北 武漢 430023；2.中國地質大學(武漢)工程學院，湖北 武漢 430074)

基坑工程中常采用降水井抽取承壓水的方式來降低地下水水位以滿足施工要求，但抽取承壓水不可避免地會引起地層沉降[1-5]。為了避免抽降承壓水對周邊建筑物或地下構筑物造成的危害，須將基坑降水引起的地層變形控制在合理的范圍內。因此，分析抽降承壓水引起的地層變形顯得尤為重要。

針對基坑降水引起的地層變形問題，許多學者進行了大量研究。如Terzaghi[6]提出土的有效應力原理，解釋了降水會引起地層中孔隙水壓力的減小致使其有效應力增加，從而導致土層產生壓縮變形；Shen等[7]通過結合三維滲流和一維土體固結的方法，提出了關于地下水開采引起地面沉降的計算方法;許燁霜等[8]在考慮了地層壓縮性的情況下，分析計算了降水引起的地面沉降問題;Shen等[9]在考慮土體固結過程中壓縮系數和滲透系數變化的條件下，建立了三維滲流和一維固結的部分耦合模型，分析了開采地下水對地面沉降的影響。但是更貼合實際的是應考慮地下水滲流和土體變形的相互作用，使滲流和應力實現真正意義上的流固耦合。為此，有不少學者基于Biot固結理論來計算抽水所引起的土體變形。如Derski[10]最早利用Biot固結理論分析了抽水所引起的土體變形問題；Booker等[11]利用Fourier積分變換，求解得到了彈性半空間體內點源穩態抽水作用下土體的Boit固結解析解；艾智勇等[12-13]利用傳遞矩陣法解決了飽和半空間或飽和成層地基中點源非穩定抽水問題；Selvadurai等[14]應用Laplace-Hankel積分變換求解得到彈性半空間無限體內某一圓盤抽水區域條件下，非穩態抽水引起的土體固結變形的解析解。此外，還有諸多學者[15-19]對此問題進行了研究。

現有的計算研究普遍建立在含水層是側向無限延伸(側向無界)假定的基礎上，缺少以在距離抽水井r=R(本文將R稱為有界半徑)處的地下水水位沒有變化為邊界條件的水位降深解答。而在工程實踐中，特別是基坑工程中，往往在距離抽水井r=R處存在補給源(如回灌源)使得該處的地下水水位不發生變化或在r=R處的地下水水位不受抽水的影響，這樣的含水系統被認為是側向有限延伸的，被稱為側向有限含水系統。此外，降水通常是通過豎向抽水井來實現的，應考慮井的完整性這一客觀事實。因此，有必要對不同側向邊界條件下完整井抽降承壓水引起的含水層變形進行分析。

在抽水過程中通常認為完整井附近的地下水壓力和流速僅隨含水層的平面方向x、y或r、θ變化，而不隨垂直方向z變化，同時還具有軸對稱的特點。基于上述完整井抽水的特點，本文在平面應力假定的基礎上[20-21]，從Biot固結方程出發，應用Laplace變換求解了越流承壓含水層在側向有界的情況下，完整井抽降水引起的承壓含水層豎向變形和徑向變形的二維解析表達，并重點分析了不同側向邊界對完整井抽降承壓水引起的含水層變形的影響。

1 模型建立及求解

1.1 基本方程

側向有界抽水承壓含水層二維變形計算示意圖見圖1。側向有界越流承壓含水層中存在一個定流量Q抽水的完整井，抽水承壓含水層均質、等厚，含水層內的滲流僅沿徑向上發生。其中，抽水承壓含水層厚度為B、滲透系數為K、彈性模量為E、泊松比為ν，且抽水承壓含水層上覆一個滲透系數為K′、厚度為B′的弱透水層，在距離抽水井r=R處存在補給源使得該處地下水水位沒有變化。

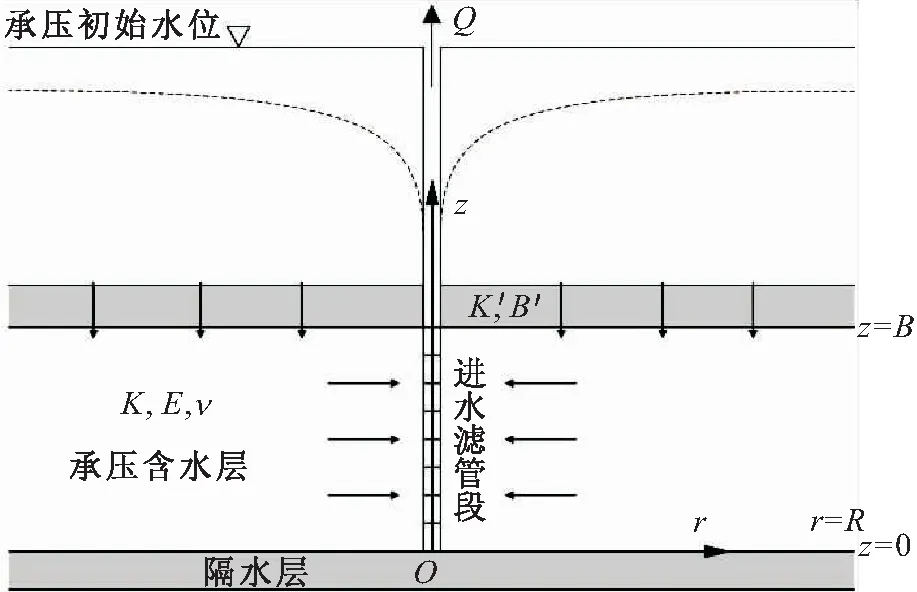
圖1 側向有界抽水承壓含水層二維變形計算示意圖Fig.1 Schematic diagram of two-dimensional deformation calculation for pumped confined aquifer of laterally finite extent in radial direction

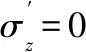
(1)

(2)

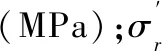
(3)

式中:ur和uz分別為徑向位移和豎向位移。

(4)

(5)

再將公式(5)對r積分，可得：

(6)

式中:f稱為無量綱積分常數，由通過在距離抽水井r=R處的邊界條件來確定。

結合方程(3)～(6)并化簡，可得到平面應力狀態下土體的基本方程如下：

(7)

(8)

(9)

1.2 固結控制方程的求解

考慮抽水承壓含水層上覆土層的越流補給，則土體質量守恒方程為

(10)

式中:K和K′分別為抽水承壓含水層和上覆弱透水層的滲透系數(cm/s)；B和B′分別為抽水承壓含水層和上覆弱透水層的厚度；γw為水的容重(kg/m3)。

將方程(7)代入方程(10)，可得：

(11)

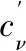
完整井以定流量Q抽水時的井壁邊界條件為

(12)

且在r=0處徑向變形為零，即：

ur(r→0,t)=0

(13)

同時，在r=R處應滿足如下條件：

p(r=R,t)=0

(14)

σrr(r=R,t)=0

(15)

將方程(11)對時間t進行Laplace變換,可得：

(16)

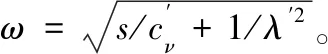
方程(16)的通解為

(17)

式中：I0為第一類0階修正貝塞爾函數；K0為第二類0階修正貝塞爾函數。

根據方程(12)和(14)可以確定方程(17)中的待定常數A1和A2，因此可以得到在Laplace空間下，孔隙水壓力的解析解為

(18)

隨后對方程(7)～(9)進行Laplace變換,并將方程(18)代入，可得：

(19)

(20)

(21)

將公式(20)對r積分，并考慮徑向變形滿足方程(13)這一條件，可得：

(22)

式中：I1為第一類1階修正貝塞爾函數；K1為第二類1階修正貝塞爾函數。

假定抽水承壓含水層底部無豎向變形，則含水層頂部豎向變形可表達為

(23)

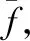
(24)

在r=R時，由方程(19)、(21)和(22),可得：

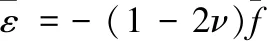
(25)

(26)

(27)

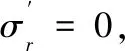
(28)

其中:

(29)

(30)

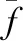
(31)

(32)

(33)

至此，得到了拉氏空間下的半解析解答，由孔隙水壓力和位移的具體表達式(31)～(33)可知，很難對其直接進行拉氏逆變換而得到時間域的解答，為此本文采用常用的Stehfest數值逆變換法[22]來求解實域解。此外，當不考慮越流影響或R→∞時，方程(31)～(33)可以簡化為完全承壓含水層或側向無限含水層情況下孔隙水壓力和變形的表達式，具體在此不做詳述。

2 分析與討論

本文在上述得到的解析解的基礎上，首先通過有限元數值計算的方法對解析解進行對比驗證，然后重點分析越流承壓含水層側向有限延伸或無限延伸條件下，完整井抽降承壓水引起的含水層豎向變形和徑向變形的特征。在無特別說明的情況下，抽水引起的含水層豎向變形和徑向變形均表示為正值。

2.1 有限元計算的對比驗證

根據上述得到的完整井抽降承壓水引起的地層變形的解析解答，將本文計算結果與COMSOL Multiphysics的有限元計算結果進行了對比。依據圖1建立了完整井抽降承壓水的簡化二維有限元計算模型。模型的水平方向尺寸設為1 000 m，由于抽水承壓含水層上覆弱透水層的越流補給是通過設置越流項來實現的，故僅需在豎直方向建立厚度為20 m的承壓含水層即可；降水井作為線源位于模型中心位置，在線源上即進水濾管處設置流量邊界以實現抽水過程，其中抽水流量Q=10 m3/h、抽水時間t=300 h；同時，上覆弱透水層的越流補給量在COMSOL Multiphysics的滲流方程中設置添加越流項即可，其最終考慮越流補給的土體質量平衡方程正如方程(10)一樣；此外，模型兩側設置水平方向的位移約束和定水頭補給邊界，模型底部設置水平和豎直兩個方向的位移約束，為不透水邊界，并在距離降水井兩側300 m位置處設置定水頭邊界，以保證抽水過程中該處地下水水位沒有變化。整個有限元計算模型共劃分為1 146個三角形單元，土體本構模型選用線彈性模型。在有限元計算和解析計算中都采用統一的土體參數值，具體土體參數值見表1。

表1 土體參數值Table 1 Values of soil parameters

表1中的土體參數取值可以如實地反映出含水砂層和黏土弱透水層的基本物理力學特性，以下在對抽水承壓含水層變形的影響分析中土層的基本參數取值與表1中一致。本文計算結果與有限元計算結果的對比，見圖2。

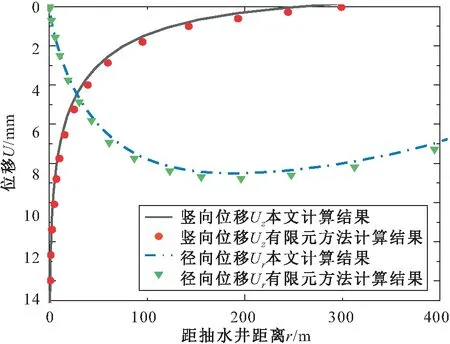
圖2 本文計算結果與有限元計算結果的對比Fig.2 Comparison of the calculation results obtained by the proposed solution and the finite element numerical solution

由圖2可見，利用本文計算方法得到的完整井抽降承壓水引起的含水層豎向位移(Uz)和徑向位移(Ur)與有限元方法的計算結果具有較好的一致性，驗證了本文計算方法的正確可靠性。

2.2 抽水承壓含水層豎向變形的影響分析

在距抽水井距離r=25 m的位置處，側向無界和有界(有界半徑R=300 m)條件下越流承壓含水層中豎向位移Uz與抽水時間t的關系曲線，見圖3。

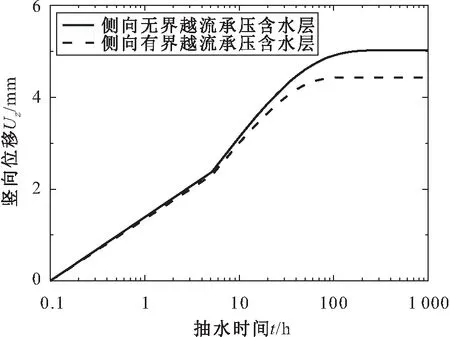
圖3 側向無界和有界(R=300 m)條件下越流承壓 含水層Uz-t的關系曲線圖Fig.3 Relation curves of the vertical deformation (Uz) versus the pumping time (t) in leaky confined aquifer of infinite and finite extent in radial direction (R=300 m)

由圖3可見，在整個抽水階段中，無論承壓含水層側向有界還是無界，其豎向位移Uz都隨著抽水時間t的增長而增大，并在后期達到穩定；當抽水時間t小于10 h時，尚未達到滲流穩定階段，抽水引起的側向有界和無界含水層的豎向位移基本是一致的，而在抽水后期，側向有界含水層相對來說更易達到穩定滲流階段，因此側向無界含水層的豎向變形要大于側向有界含水層。

當抽水時間t=300 h時，側向無界和有界(R=200 m)條件下越流承壓含水層的豎向位移Uz與距抽水井距離r的關系曲線，見圖4。

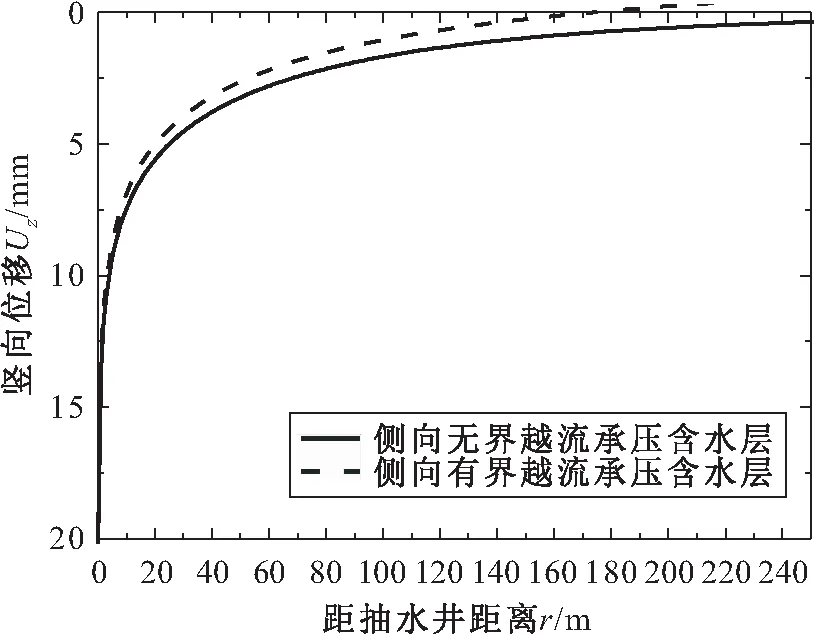
圖4 側向無界和有界(R=200 m)條件下越流承壓 含水層中Uz-r的關系曲線圖Fig.4 Relation curves of the vertical deformation (Uz) versus the distance (r) in leaky confined aquifer of infinite and finite extent in radial direction (R=200 m)

由圖4可見，從含水層土體變形的整體規律上看，無論越流承壓含水層是側向有界還是無界，抽水引起的含水層豎向位移Uz均隨著與抽水井距離r的增大而減小；在抽水滲流達到穩定階段時，側向無界含水層的豎向變形量要大于側向有界含水層，且這種變形量的差異在距離抽水井越遠的位置越發明顯，這是由于越接近側向邊界(R=200 m)，受到側向邊界補給作用的影響更加明顯，從而減小了抽水井對豎向變形的影響。

當有界半徑R取不同值時，越流承壓含水層的豎向位移Uz見圖5，為了比較分析，側向無界含水層中抽水的情況也考慮其中。

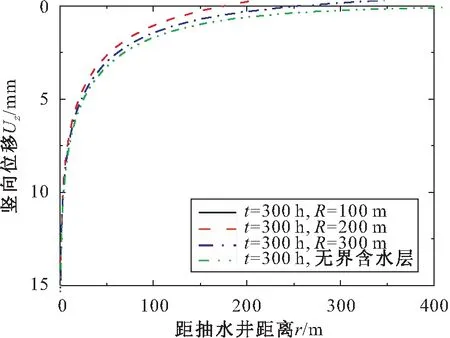
圖5 不同有界半徑R對越流承壓含水層豎向位移 Uz的影響Fig.5 Impact of finite radius (R) on the vertical deformation of leaky confined aquifer

由圖5可見，在較長的抽水時間(t=300 h)內，隨著有界半徑R的增大，側向有界含水層的豎向位移Uz越接近于側向無界含水層；在抽水達到穩定滲流階段后，隨著有界半徑R的增大，側向有界含水層的豎向變形范圍和具體量值均隨之增大，這是由于側向邊界越接近于抽水井，其補給作用對抽水的影響則越明顯，從而減小了抽水井所能引起的含水層豎向變形范圍和豎向變形量。

2.3 抽水含水層徑向變形的影響分析

在距抽水井距離r=25 m位置處，抽水引起的側向無界和有界(R=200 m)越流承壓含水層的徑向變形Ur與抽水時間t的關系曲線，見圖6。

圖6 側向無界和有界(R=200 m)條件下越流承壓 含水層Ur-t的關系曲線Fig.6 Relation curves of the vertical deformation (Uz) versus the pumping time (t) in leaky confined aquifer of infinite and finite extent in radial direction (R=200 m)

由圖6可見，在整個抽水階段中，側向無界和有界越流承壓含水層的徑向變形Ur均隨著抽水時間t的增長而增大，并在達到穩定滲流時保持不變，且此時含水層徑向位移達到最大值；此外，在相同的抽水時間，距離抽水井同一位置處側向無界承壓含水層的徑向位移要小于側向有界承壓含水層，這是由于在側向有界承壓含水層中，側向邊界位置(有界半徑R)處的地下水水位始終保持不變，抽水過程中會形成一個相比于側向無界承壓含水層中更大的水頭差和滲流力作用，從而引起含水層更大的徑向變形。

在不同抽水時間t=50 h和t=300 h時，側向無界和有界(R=200 m)條件下越流承壓含水層的徑向位移Ur與距抽水井距離r的關系曲線，見圖7。

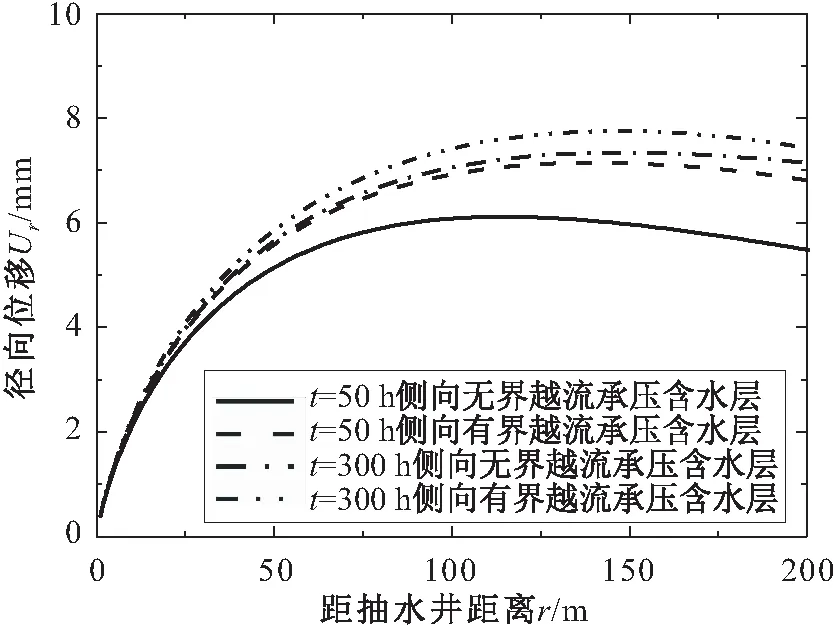
圖7 不同抽水時間側向無界和有界條件下越流承壓 含水層Ur-r的關系曲線Fig.7 Relation curves of the radial deformation (Ur) versus the distance (r) in leaky confined aquifer of infinite and finite extent in radial direction under different pumping time

由圖7可見，在同一抽水時間，側向無界和有界承壓含水層的徑向位移Ur沿徑向的分布規律基本一致，即隨著距抽水井距離r越遠，側向有界和無界承壓含水層徑向位移Ur呈現先增大后減小的趨勢，這是由于靠近抽水井位置附近的側向有界和無界承壓含水層處于壓縮變形區，距離抽水井較遠位置的側向有界和無界承壓含水層處于拉張變形區，而側向有界和無界承壓含水層的最大徑向變形會出現在這兩個區域的交界位置處，因此越流承壓含水層的最大徑向變形出現在距抽水井一定距離處。

當有界半徑R取不同值時，越流承壓含水層的徑向位移Ur見圖8，為了比較分析，側向無界含水層中抽水的情況也考慮其中。

圖8 不同有界半徑R對越流承壓含水層徑向位移 Ur的影響Fig.8 Impact of finite radius (R) on the radial deformation of leaky confined aquifer(Ur)

由圖8可見，在較長的抽水時間(t=300 h)內，隨著有界半徑R的增大，抽水井引起的側向有界承壓含水層的徑向變形量和變形范圍均隨之增大，這是由于有界半徑R越大，側向邊界對抽水的影響越小，抽水所能引起的含水層徑向變形量和變形范圍也就越大；同時，隨著側向邊界與抽水井相距越遠，含水層的拉張變形區也相對距離抽水井越遠，進而導致含水層壓縮變形區和拉張變形區的交界位置也越遠離抽水井，最終呈現如圖8所示含水層最大徑向變形位置隨著有界半徑R的增大而遠離抽水井這一特征；此外，側向無界條件下含水層的徑向變形規律與側向有界條件有所差異，這是由于側向邊界的補給作用減小了抽水井對含水層徑向變形的影響范圍，從而導致側向無界承壓含水層的徑向變形范圍要大于側向有界承壓含水層。

3 結 論

本文建立并得到了完整井抽降水引起的側向有界越流承壓含水層豎向位移和徑向位移的解析解，并重點分析了完整井抽水條件下側向邊界對越流承壓含水層豎向變形和徑向變形的影響，得到主要結論如下：

(1) 無論抽水承壓含水層側向有界還是無界，在整個抽水階段，承壓含水層的豎向變形在抽水前期均隨著抽水時間的增長而增大，并在后期達到穩定保持不變，抽水引起的承壓含水層豎向變形也隨著距抽水井距離的增大而減小；在達到滲流穩定階段后，側向無界承壓含水層的豎向變形量要大于側向有界承壓含水層，且這種變形量的差異在距離抽水井越遠的位置越發明顯。

(2) 在抽水達到穩定滲流階段時，隨著有界半徑R的增大，抽水引起的側向有界承壓含水層的豎向變形范圍和具體變形量值均隨之增大，且其豎向變形的分布規律也越接近于側向無界承壓含水層的情況。

(3) 在整個抽水階段，側向無界和有界越流承壓含水層的徑向變形均隨著抽水時間的增長而增大，并在達到穩定滲流時保持不變且承壓含水層達到最大徑向位移值；在同一抽水時間，隨著距抽水井距離的增大，側向無界和有界承壓含水層的徑向位移呈現出先增大后減小的變化規律，即越流承壓含水層的徑向位移的最大值出現在距抽水井一定距離處，且側向無界承壓含水層的徑向變形量要小于側向有界承壓含水層。

(4) 在抽水達到穩定滲流時，隨著有界半徑R的增大，抽水引起的側向有界承壓含水層的徑向變形量和變形范圍也隨之增大，其最大徑向變形位置也隨之遠離抽水井，且抽水引起的側向無界承壓含水層的徑向變形范圍要大于側向有界承壓含水層。