萬變不離其宗
———一道三角函數題的破解

◇ 山東 張海艷

三角函數是每年高考中的熱門考點,而最為常見的是三角函數的圖象與性質問題.此類問題一般通過三角函數的定義、公式、圖象與性質等的考查來達到應用的目的,難度中等,但運算量大,技巧性強.

1 問題呈現

題目已知函數其中上恒成立,則的最大值為( ).

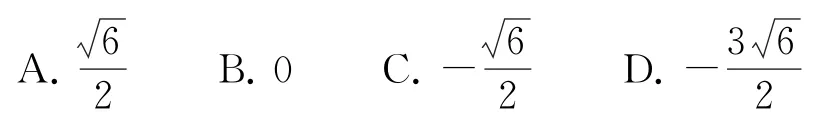
此題以三角函數為載體,結合三角函數的含參關系式以及三角不等式恒成立的條件,來確定對應三角函數值的最值問題.通過巧妙設置,把三角函數中的幾大知識點加以融合,充分考查了三角函數的圖象與性質、三角不等式以及恒成立問題等,是考查三角函數知識的一大亮點與創新點.

2 問題破解

解法1(三角不等式討論法)由于可得而恒成立,則有又由于φ＜2x＋φ＜所以

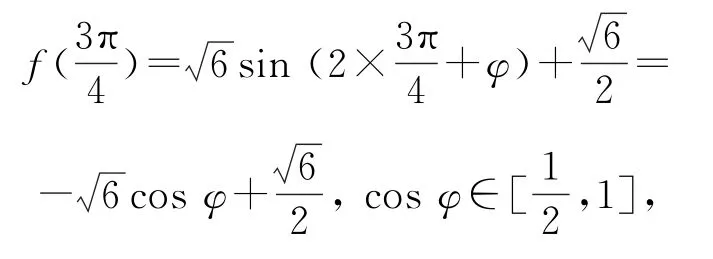
點評

解法1根據三角不等式恒成立的條件,綜合考查三角函數的圖象與性質,這是解決此類問題的一般方法.破解的關鍵就是有效綜合三角不等式恒成立的求解以及三角函數的圖象與性質來確定含參變量的取值范圍,為進一步確定三角函數的最值奠定基礎.

解法2(排除法)由于直接排除選項D;又是最小值,不符合題目條件,可以排除選項C;假設是最大值,此時解得cosφ＝0,結合可得2x∈時,

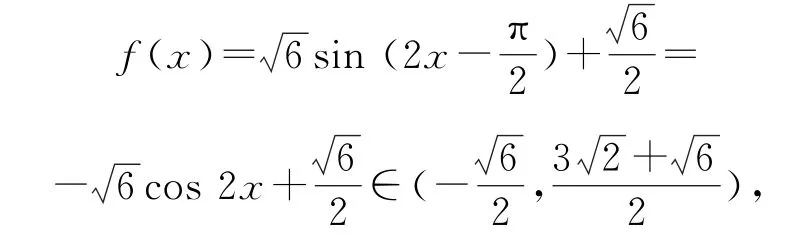
f(x)＞0不恒成立;當時,

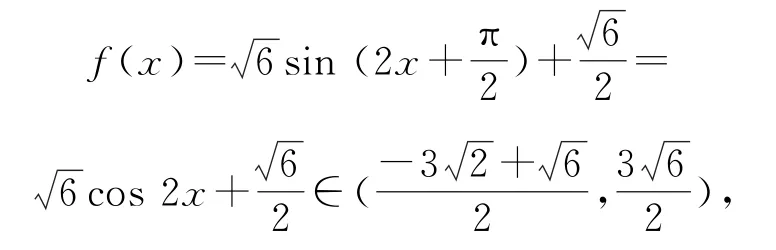
f(x)＞0也不恒成立,所以可以排除選項A.故選B.

點評

涉及三角函數的一些選擇題,排除法有時是一種非常有效、快捷的方法.充分利用三角函數的圖象與性質,借助各選項之間的關系,可以巧妙地加以分析與排除,間接處理,從而達到正確破解問題的目的.