基于柔性機構捕捉衛(wèi)星的空間機器人動態(tài)緩沖從順控制1)

艾海平 陳 力

(福州大學機械工程及自動化學院,福州 350116)

引言

近年來隨著空間技術的發(fā)展及人類對太空探索的進一步深入,空間機器人被期望在太空服務中扮演更重要的角色并執(zhí)行更復雜的任務:如失效航天器的維修、在軌燃料加注、在軌裝配和后勤支援等[1-5],以實現(xiàn)延長在軌航天器服務壽命、提升在軌服務性能的目的,因此對其的研究引起了國內(nèi)外學者的諸多關注[6-13].同時,因發(fā)射失敗及在軌故障導致失效的航天器日益增多,進而影響了空間在軌服務任務的執(zhí)行.考慮太空軌道資源的寶貴及失效衛(wèi)星回收的經(jīng)濟價值,空間機器人對失效衛(wèi)星的捕獲操作研究具有重要意義[14-18].

空間機器人執(zhí)行在軌捕獲操作時,不可避免的要與目標衛(wèi)星發(fā)生接觸、碰撞,在此過程,其機械臂將會受到很大的碰撞沖擊力矩[19-20],若沖擊力矩過大,很可能對最薄弱的關節(jié)處造成破壞.考慮非合作衛(wèi)星一般具備高速、旋轉等特性,空間機器人對其進行捕獲操作時,其遭受的沖擊力矩將使關節(jié)處遭受損壞,并導致空間任務的失敗.因此,在捕獲操作過程采取一定措施以避免空間機器人的關節(jié)電機受到?jīng)_擊而破壞是極其必要的.然而,目前關于空間機器人避免關節(jié)遭受沖擊破壞的研究卻鮮見報道,故對其的研究有著重要的探索價值和意義.

針對空間機器人在軌捕獲操作的研究,國內(nèi)外學者已經(jīng)取得了一定的成果.Uyam 等[21]對空間機器人與自由漂浮衛(wèi)星的接觸效應進行了實驗的評估.Rekleitis 等[22]研究了近距離捕獲被動航天器的控制問題,設計了基于模型的控制算法.程靖等[19]研究了空間機器人捕獲衛(wèi)星過程動力學演化模擬,并設計了模糊H∞控制方案以實現(xiàn)不穩(wěn)定系統(tǒng)的鎮(zhèn)定.Meng 等[23]針對含柔性構件空間機器人自主捕獲目標前的彈性振動抑制問題,基于動態(tài)耦合模型設計了一個閉環(huán)控制系統(tǒng).Aghili 等[24]研究了空間機械臂捕獲衛(wèi)星的最優(yōu)控制問題,實現(xiàn)了聯(lián)合體系統(tǒng)的最小時間鎮(zhèn)定.Dong 等[25]研究了衛(wèi)星自主交會對接過程位置及姿態(tài)的控制問題.Lampariello 等[26]設計了一種基于非線性優(yōu)化的方法,以實現(xiàn)有限時間內(nèi)對翻滾目標的捕獲.Stolfi 等[27]提出了一種基于PD控制的阻抗算法,以實現(xiàn)對非合作目標的捕獲.值得一提的是,以上研究成果主要關注的是捕獲前軌跡規(guī)劃及捕獲后組合體的鎮(zhèn)定控制上,并未考慮減小空間機器人捕獲衛(wèi)星碰撞過程所受沖擊力矩及實現(xiàn)鎮(zhèn)定過程對關節(jié)電機的保護.

考慮到柔性機構—RSEA(rotary series elastic actuator)在機器人與外界環(huán)境發(fā)生碰撞時,在保護機器人關節(jié)執(zhí)行器避免外部沖擊破壞方面發(fā)揮了很好的作用[28-29].為此,本文嘗試將RSEA 引入到空間機器人系統(tǒng)中,同時設計與之配合的開啟、關閉電機策略以實現(xiàn)緩沖從順控制.然而由于RSEA 裝置存在緩沖彈簧,因此也為系統(tǒng)帶來了關節(jié)柔性.此外,空間機器人自身各構件間存在著強耦合作用,捕獲過程系統(tǒng)內(nèi)部還會存在動量、動量矩及能量的傳遞變化.以上多重問題的綜合使得空間機器人在軌捕獲衛(wèi)星的動力學與控制研究大為復雜.

對于高性能的空間機械臂來說,關節(jié)柔性是一個不可忽略的影響因素,為了實現(xiàn)存在關節(jié)柔性的空間機器人的緩沖從順控制,本文基于奇異攝動思想,將空間機器人及被捕獲衛(wèi)星形成的聯(lián)合體系統(tǒng)分解為表征柔性部分的快變子系統(tǒng)及表征剛性部分的慢變子系統(tǒng).針對快變子系統(tǒng),設計了速度差值反饋控制器以主動抑制系統(tǒng)的彈性振動.考慮星載計算機的運算能力有限,而捕獲操作將導致液體燃料晃動而產(chǎn)生擾動項.鑒于自抗擾控制(active disturbance rejection control,ADRC)技術可對擾動項進行動態(tài)估計,并實時補償[30-31].因此,對慢變子系統(tǒng)提出了一種基于動態(tài)面的自抗擾控制器.所提方法避免了反演法帶來的計算膨脹問題,有效減少了星載計算機的計算量[32-33].同時,有效提升了不穩(wěn)定聯(lián)合體系統(tǒng)的抗擾動能力,并最終達到穩(wěn)定控制及軌跡的精確跟蹤.最后,通過對空間機器人捕獲操作過程的仿真分析,表明了柔性機構的抗沖擊性能及所提緩沖從順控制策略的有效性.

1 柔性機構結構及緩沖從順策略

配置柔性機構空間機器人系統(tǒng)的RSEA 裝置安裝在電機與機械臂之間,通過其輸入圓盤與電機相連,機械臂則是與RSEA 裝置的掃臂負載空心軸相連.空間機械臂總體結構簡圖如圖1 所示,所設計RSEA 裝置的結構如圖2 所示.圖2 中R為掃臂有效半徑,r為彈簧的半徑.

圖1 空間機械臂結構圖Fig.1 Structure of space manipulator

圖2 RSEA 裝置結構圖Fig.2 Structure of RSEA

在捕獲階段,機械臂末端與目標衛(wèi)星發(fā)生碰撞,其關節(jié)處會受到很大的沖擊力矩,該力矩先作用在RSEA 裝置的輸出掃臂上,再傳遞到彈簧組,通過內(nèi)部彈簧對碰撞能量進行吸收、緩沖,進而實現(xiàn)對關節(jié)的保護.在鎮(zhèn)定運動階段,受沖擊效應的影響,電機開啟時也會受到?jīng)_擊力矩,若所受力矩超過電機所能承受的極限而不關停電機,電機將遭受損壞.因此,需要根據(jù)關節(jié)所能承受的力矩極限設置一個關機力矩閾值讓電機關停.當檢測到關節(jié)所受沖擊力矩超過所設關機力矩閾值后電機關停,此時,RSEA 裝置內(nèi)部彈簧組會提供彈力以減小關節(jié)所受沖擊力矩.此外,在實際操作中,若是只設定關機力矩閾值,將導致電機頻繁開關機,進而影響電機性能.基于此,本文所提的從順控制策略設置了兩個力矩閾值,一個是電機關機力矩閾值,另一個是電機開機力矩閾值.當關節(jié)所受力矩超過關機力矩閾值時,電機關停,當關節(jié)所受力矩低于開機力矩閾值時,電機再次開機.

2 動力學建模及沖擊效應分析

以配置RSEA 空間機器人捕獲衛(wèi)星操作過程為例,如圖3 所示.建立系統(tǒng)慣性坐標系XOY,同時建立各分體的連體坐標系xiOiyi(i=0,1,2),其中O0為基座質心;Oi(i=1,2)為連接各關節(jié)的轉動鉸中心.設空間機器人系統(tǒng)基座B0質量、質心轉動慣量及O0至O1長度分別為m0,I0,l0;機械臂質量、質心轉動慣量及長度分別為mi,Ii,li(i=1,2);di為第i個關節(jié)轉動鉸中心到機械臂i質心的距離.被捕獲衛(wèi)星的質量、質心轉動慣量為mt和It.兩關節(jié)電機轉子轉動慣量為Iim(i=1,2);RSEA 裝置中彈簧的剛度為kia(i=1,2).θ0,θi(i=1,2)和θt分別為基座姿態(tài)、機械臂、被捕獲衛(wèi)星轉動角;θim(i=1,2)為電機轉子轉角.系統(tǒng)總質心及基座、機械臂質心在慣性坐標系下位置矢量分別為rc,r0,r1和r2.

圖3 空間機器人系統(tǒng)及目標衛(wèi)星系統(tǒng)Fig.3 Space robot and target satellite systems

將目標衛(wèi)星視為均質剛體,定義qt=[xt,yt,θt]T為其廣義坐標列向量,則可通過牛頓?歐拉法獲得被捕獲衛(wèi)星系統(tǒng)的動力學方程

其中,Dt∈R3×3為被捕獲衛(wèi)星系統(tǒng)廣義質量陣,xt和yt為被捕獲衛(wèi)星質心位置坐標;Jt∈R3×3為被捕獲衛(wèi)星碰撞接觸點對應的運動Jacobian 矩陣,F′∈R3×1為被捕獲衛(wèi)星所受到的作用力.

根據(jù)圖3 中幾何位置關系,可得捕獲前空間機器人各分體質心在慣性坐標系下的表達式為

其中,xa和ya為載體質心位置坐標;ei(i=0,1,2)為各連體坐標系xi方向的基矢量.

對式(2)、式(3)進行求導,可得到含柔性機構空間機器人系統(tǒng)總動能表達式為

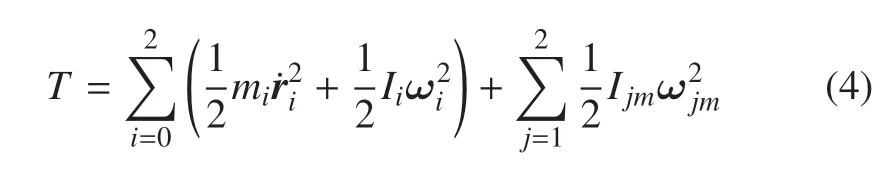
其中,ωi(i=0,1,2)表示載體及兩機械臂桿的角速度;ωjm(j=1,2)表示電機轉子的角速度.

忽略太空微弱重力影響,可知空間機器人系統(tǒng)勢能只來源于RSEA 裝置,因而其總勢能為

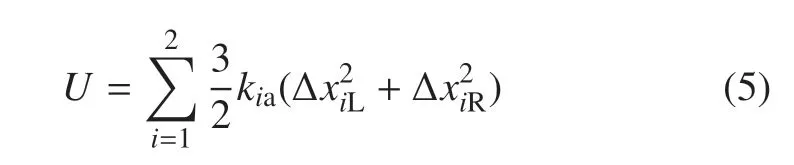
其中,kia(i=1,2)為關節(jié)等效剛度,其計算公式于仿真處給出;?xiL=Rsin(αi),?xiR=?Rsin(αi);αi為輸入圓盤與掃臂之間的角度差.

基于上述動能、勢能表達式,可得到Lagrange 函數(shù),結合第二類拉格朗日建模方法,推導得捕獲碰撞前載體位置不受控、姿態(tài)受控的空間機器人動力學方程為

其中,q=[xa,ya,θ0,θ1,θ2]T為空間機器人系統(tǒng)廣義坐標;θm=[θ1m,θ2m]T,θ=[θ1,θ2]T;D(q)∈R5×5表示系統(tǒng)廣義質量陣,為系統(tǒng)包含科氏力、離心力項;,τa=02×1,τ0為載體姿態(tài)控制力矩,τθ為關節(jié)輸入力矩,τm=[τ1m,τ2m]T為電機輸出力矩;Jm=diag(I1m,I2m)為電機轉子轉動慣量;Km=diag(k1m,k2m);J∈R3×5為機械臂末端對應的運動Jacobian 矩陣;F∈R3×1為機械臂末端所受作用力.

在捕獲操作過程,空間機器人與被捕獲衛(wèi)星兩者發(fā)生接觸、碰撞,其相互作用力滿足牛頓第三定律,即:F=?F′.基于此并結合式(1)、式(6),可得

由于捕獲過程空間機器人與目標衛(wèi)星形成的系統(tǒng)未受外力作用,所以整個系統(tǒng)服從動量守恒關系;此外,為保護關節(jié)電機,捕獲階段電機將處于關機狀態(tài),即τc=05×1,因此,對式(7)兩端進行積分并整理得[19]

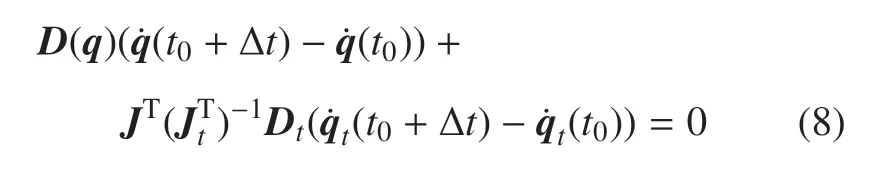
捕獲完成后,空間機器人與目標衛(wèi)星形成聯(lián)合體系統(tǒng),兩者末端接觸點滿足速度約束,即自t0+?t時刻恒有

結合式(8)、式(9),可得碰撞沖擊對空間機器人運動狀態(tài)的影響

通過對式(6)第一項進行積分,可得捕獲階段的碰撞沖量

其中,P=為碰撞沖量.結合式(10)、式(11),可計算得碰撞沖量表達式為

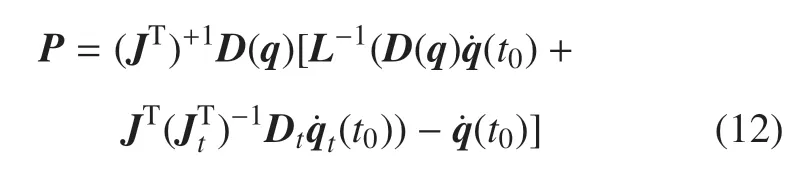
其中,(JT)+1為JT的偽逆.由于捕獲碰撞時間?t極小,則碰撞力可以近似為

捕獲操作完成后,空間機器人與被捕獲衛(wèi)星兩者形成聯(lián)合體系統(tǒng),因此其末端滿足式(9)的速度約束,對式(9)進行求導,并整理化簡得

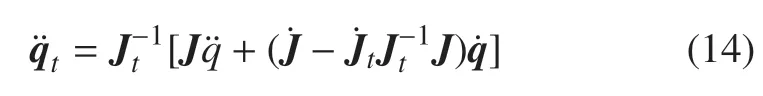
結合式(6)、式(7)、式(14),可得聯(lián)合體系統(tǒng)的綜合系統(tǒng)動力學方程為

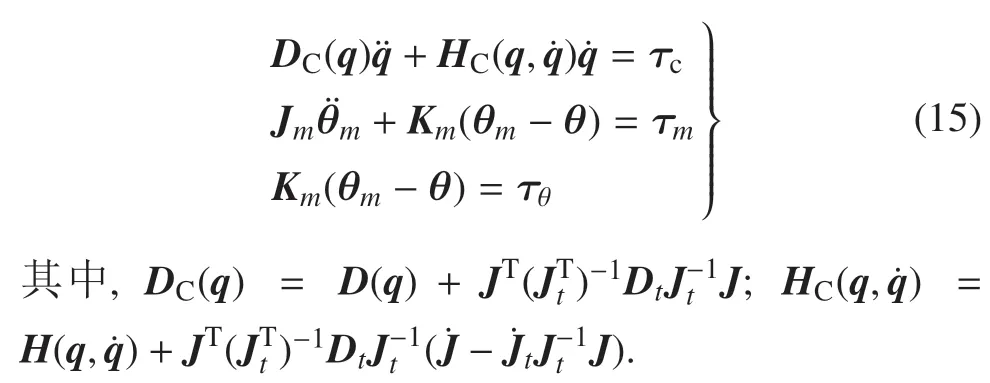
考慮空間機器人系統(tǒng)在軌服務壽命等原因,載體位置處于不受控的狀態(tài).基于此,式(15)表現(xiàn)為欠驅動形式,其不利于控制的設計.為將式(15)化為全驅動形式,將其寫成如下分塊子矩陣形式

其中,qa=[xa,ya]T,qθ=[θ0,θ1,θ2]T;τb=.通過觀察發(fā)現(xiàn)HC11和HC21均為零矩陣,基于此由式(16)第一行可解得的表達式,并代入第二行,可得到聯(lián)合體系統(tǒng)全驅動形式動力學方程

3 控制器設計

3.1 快變子系統(tǒng)控制器設計

由于聯(lián)合體系統(tǒng)存在RSEA 裝置,其使得系統(tǒng)關節(jié)具備柔性,為了抑制關節(jié)柔性引起的振動,借助奇異攝動技術,將聯(lián)合體系統(tǒng)分解為快變子系統(tǒng)和慢變子系統(tǒng)分別進行控制設計,因此系統(tǒng)的總控制律可寫為如下形式

其中,τs∈R2×1為慢變子系統(tǒng)控制力矩,τf∈R2×1為快變子系統(tǒng)控制力矩.

定義正比例因子ε 及正定對角矩陣K1,并令其滿足如下關系

結合式(19),則式(17)的后兩項可重寫為描寫系統(tǒng)彈性振動的快變子系統(tǒng)方程

設計如下速度差值反饋控制器對快變子系統(tǒng)進行控制

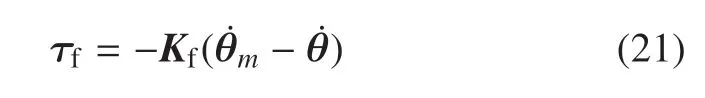
其中,Kf=K2/ε,K2∈R2×2為正定、對角矩陣.

將式(18)、式(21)代入式(20),可得

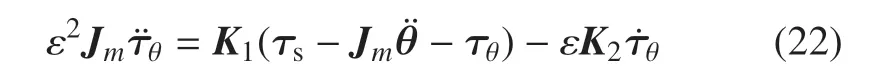
當ε →0 時,關節(jié)等效剛度K→∞,此時聯(lián)合體系統(tǒng)等效為剛性模型;則由式(17)、式(18)可得出慢變子系統(tǒng)的動力學方程

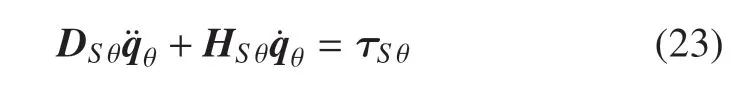
其中,DSθ=DX+JX,HSθ為時對應的新矩陣;JX=diag(0,I1m,I2m),τSθ=.

3.2 慢變子系統(tǒng)控制器設計

考慮捕獲操作將導致控制載體姿態(tài)的液體燃料晃動,進而產(chǎn)生有界擾動項,則慢變子系統(tǒng)動力學方程式(23)可寫為

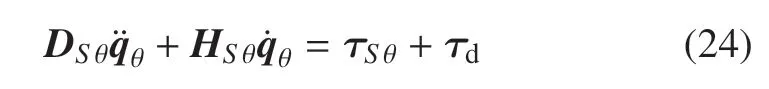
其中,τd∈R3×1為擾動項.

為便于分析,令x1=qθ,x2=,則式(24)可表示為如下形式狀態(tài)方程

考慮星載計算機的運算能力有限,借助動態(tài)面技術簡化運算過程.慢變子系統(tǒng)動態(tài)面控制設計步驟如下.

(1)定義軌跡跟蹤誤差,即第一個誤差面

其中,qθd∈R3×1為系統(tǒng)軌跡期望矢量.

對式(26)兩邊進行求導,可整理得

定義虛擬控制量,其滿足

其中,η1為正常數(shù).

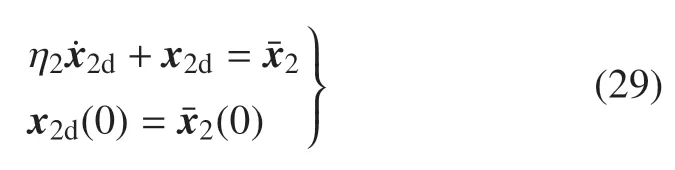
其中,時間η2>0.

(2)為設計慢變子系統(tǒng)控制律,定義第二個誤差面

對s2兩邊進行求導,并結合式(25),可得

考慮有界擾動項將影響鎮(zhèn)定運動的穩(wěn)定性及軌跡跟蹤精度,因此采用擴張狀態(tài)觀測器對其進行動態(tài)估計,擴張狀態(tài)觀測器設計如下

其中,λ>0 為觀測器帶寬.

在上述基礎上,慢變子系統(tǒng)控制律設計如下

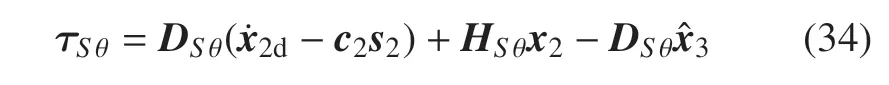
其中,c2為正定、對角矩陣.

定義狀態(tài)變量ωi=,ω=.由式(25)、式(32),可得

其中,Kv=.

定理1若是有界的,任意選取觀測器帶寬λ >0,觀測誤差服從一致有界性,即:滿足存在常數(shù)γi>0,使得中所有元素在有限時間內(nèi)滿足≤γi(j=1,2,3).

證明假設觀測器誤差初始為零,對式(35)進行求解,可得

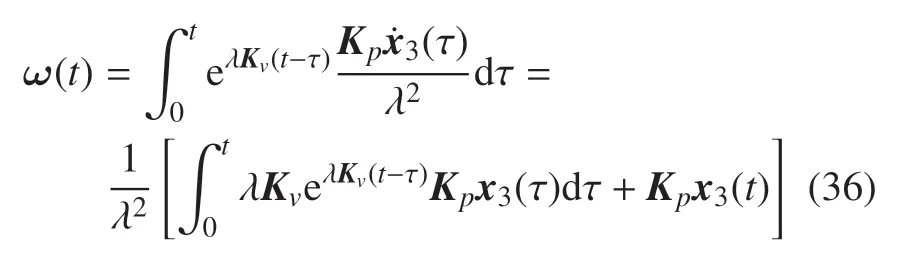
參考文獻[35] 相關推導可知,若Kv是Hurwitz的,則存在時間ts,在t≥ts的任意時刻,滿足如下關系

因此,ω(t)中各個元素滿足如下關系

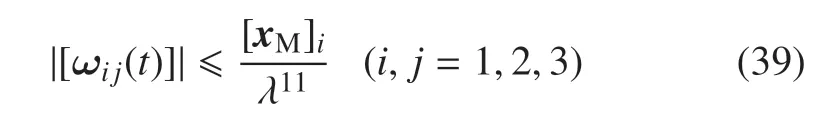
結合ωi=可得

綜合以上分析,可證明擴張狀態(tài)觀測器的觀測誤差服從一致有界性.證畢.

定理2對于式(25)所示的慢變子系統(tǒng),基于所設計控制器(34),可保證聯(lián)合體系統(tǒng)半全局最終一致有界.

證明結合所設計動態(tài)面,定義系統(tǒng)邊界層誤差如下

結合式(29)及式(41),可得

由此可解得z2的一階導數(shù)

聯(lián)立式(27)～式(30)及式(42),有

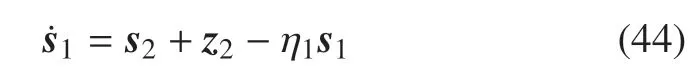
定義如下Lyapunov 函數(shù)

對式(45)進行求導,可得

將式(34)代入式(31)中,得到

根據(jù)式(43)、式(44)、式(47),將其代入式(46)可有

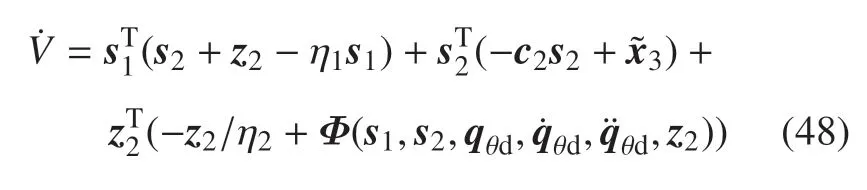
利用Young 不等式得

進而,式(48)滿足

參考文獻[36] 可知,||Φ||≤ψ,(ψ >0),選取1/η2≥1/2+ψ2/(2k)+a0,可得到

其中?=min{2(η1?1),2(c2?1),2a0},ρ=+k/2.

通過對? 適當選取,使其滿足? >ρ/?,則當V=? 時,≤0 是一個不變集,即存在V(0)≤?,則對t>0 時,恒有V(t)≤?.

求解式(50)可得

基于上述條件,并結合Lyapunov 穩(wěn)定性定理,可知該系統(tǒng)以ρ/? 為界,聯(lián)合體系統(tǒng)半全局最終一致有界.因此,聯(lián)合體系統(tǒng)軌跡跟蹤誤差e可收斂到零的任意小鄰域.證畢.

4 仿真算例分析

4.1 捕獲碰撞過程RSEA 抗沖擊性能模擬

采用圖3 所示的空間機器人及目標衛(wèi)星系統(tǒng)進行數(shù)值仿真試驗.模型參數(shù)選取如下:m0=80 kg,I0=40 kg·m2,l0=1 m;mi=5 kg,Ii=3 kg·m2,li=2 m,di=1 m(i=1,2);mt=30 kg,It=15 kg·m2,lt=0.5 m;I1m=I2m=0.05 kg·m2,k1a=k2a=1000 N/m.關節(jié)等效剛度的計算公式[28]為

其中,Ka=diag(k1a,k2a),R=0.1 m,r=0.01 m,φ為機械臂末端施加τF=[20 Nm,20 Nm,0 Nm]T的載荷時掃臂的轉角,仿真時選取φ=diag(3?,2?).

為了驗證空間機器人碰撞過程的抗沖擊性能,采用配置/未配置RSEA 裝置空間機器人系統(tǒng)對不同初速度衛(wèi)星進行捕獲模擬試驗,選取空間機器人系統(tǒng)的初始構型為q=[0,0,90?,45?,45?]T,碰撞所受沖擊力矩結果如表1 所示.表1 中,第二及第三列前、后項分別為未配置與配置RSEA 裝置關節(jié)所受沖擊力矩;第四列為沖擊力矩最大降低百分比.

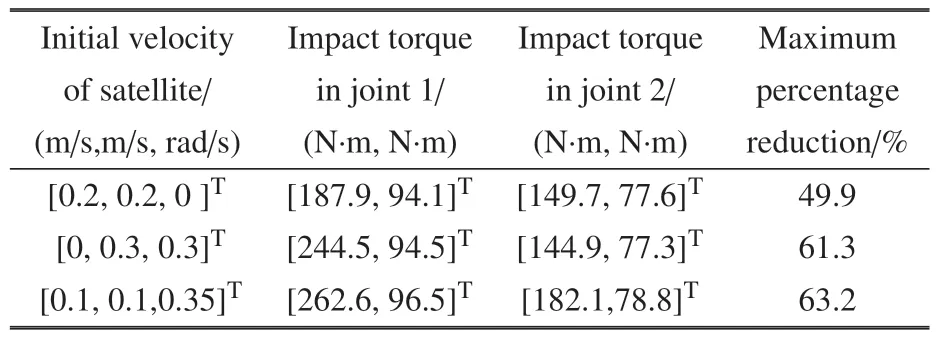
表1 衛(wèi)星不同初速度下RSEA 的抗沖擊性能模擬Table 1 RSEA impact resistance at different satellite initial velocities

由表1 可看出,針對捕獲不同初速度衛(wèi)星的操作過程,配置RSEA 裝置較未配置RSEA 裝置都能有效的減小空間機器人關節(jié)所受碰撞沖擊力矩,進而實現(xiàn)了對關節(jié)的保護.

4.2 鎮(zhèn)定運動過程緩沖從順控制策略性能模擬

為驗證鎮(zhèn)定運動過程緩沖從順控制策略的有效性,運用本文第三部分所提控制方案對圖3 所示系統(tǒng)進行數(shù)值仿真試驗.所提控制方案的控制參數(shù)選取如下:K2=diag(5,5),c2=diag(5,5,5),ε=0.5,α1=diag(9,9,9),α2=diag(27,27,27),α3=diag(27,27,27).由捕獲產(chǎn)生的擾動項為τd=[2 sin(πt/3)?2 cos(πt/3),2 sin(πt/3),2 cos(πt/3)]T.假設在t0=0 時空間機器人對衛(wèi)星進行捕獲操作,此時衛(wèi)星速度為vt=[0.1 m/s,0.1 m/s,0.35 rad/s]T.捕獲完成后空間機器人與目標衛(wèi)星形成的聯(lián)合體系統(tǒng)期望位置選取為qθd=[100?,30?,60?]T.仿真時間選取為t=20 s.仿真結果如圖4～圖8 所示.

圖4 未采用開、關機策略關節(jié)所受沖擊力矩Fig.4 Joint impact torque without switching strategy

圖5 采用開、關機策略關節(jié)所受沖擊力矩Fig.5 Joint impact torque with switching strategy

圖6 關節(jié)電機開、關機信號Fig.6 Switch signal of joint motor

圖4 為未開啟主動開、關電機策略時,關節(jié)所受沖擊力矩.假設關節(jié)電機正常工作時,所能承受的沖擊力矩極限為80 N·m.可發(fā)現(xiàn)此時的沖擊力矩雖然較未配置柔性機構得到降低,但依然超出安全閾值.因此需結合開、關機策略進行控制,以實現(xiàn)對關節(jié)電機的保護;選取電機關機閾值為τO=48 N·m,開機閾值為τI=9 N·m.圖5 及圖6 分別為開啟所提開、關機策略時,關節(jié)所受沖擊力矩及關節(jié)電機開關機情況.對比圖4 與圖5 可知,結合緩沖從順控制,可使得關節(jié)所受沖擊力矩限制在安全范圍內(nèi),有效實現(xiàn)了對關節(jié)電機的保護.

圖7 開啟緩沖從順控制時鎮(zhèn)定運動軌跡Fig.7 Trajectory tracking of stabilization under buffer and compliant control

圖7 為采用上述緩沖從順控制時的鎮(zhèn)定軌跡.其中,實線為結合自抗擾補償?shù)膭討B(tài)面控制方法時的鎮(zhèn)定軌跡,虛線為關閉自抗擾補償項時的鎮(zhèn)定軌跡.通過兩種方法對比可知,所提基于動態(tài)面的自抗擾控制方法可有效實現(xiàn)對擾動項的補償,并更快實現(xiàn)了對受擾動聯(lián)合體系統(tǒng)的鎮(zhèn)定控制,有效提升了失穩(wěn)聯(lián)合體系統(tǒng)抗擾動的能力.

圖8 為關閉其快變子系統(tǒng)速度差值反饋控制器時,所得的跟蹤軌跡情況;比較圖7 與圖8 可知,所提速度差值反饋控制器,可實現(xiàn)對系統(tǒng)關節(jié)彈性振動的主動抑制,進而達到軌跡的精確跟蹤.

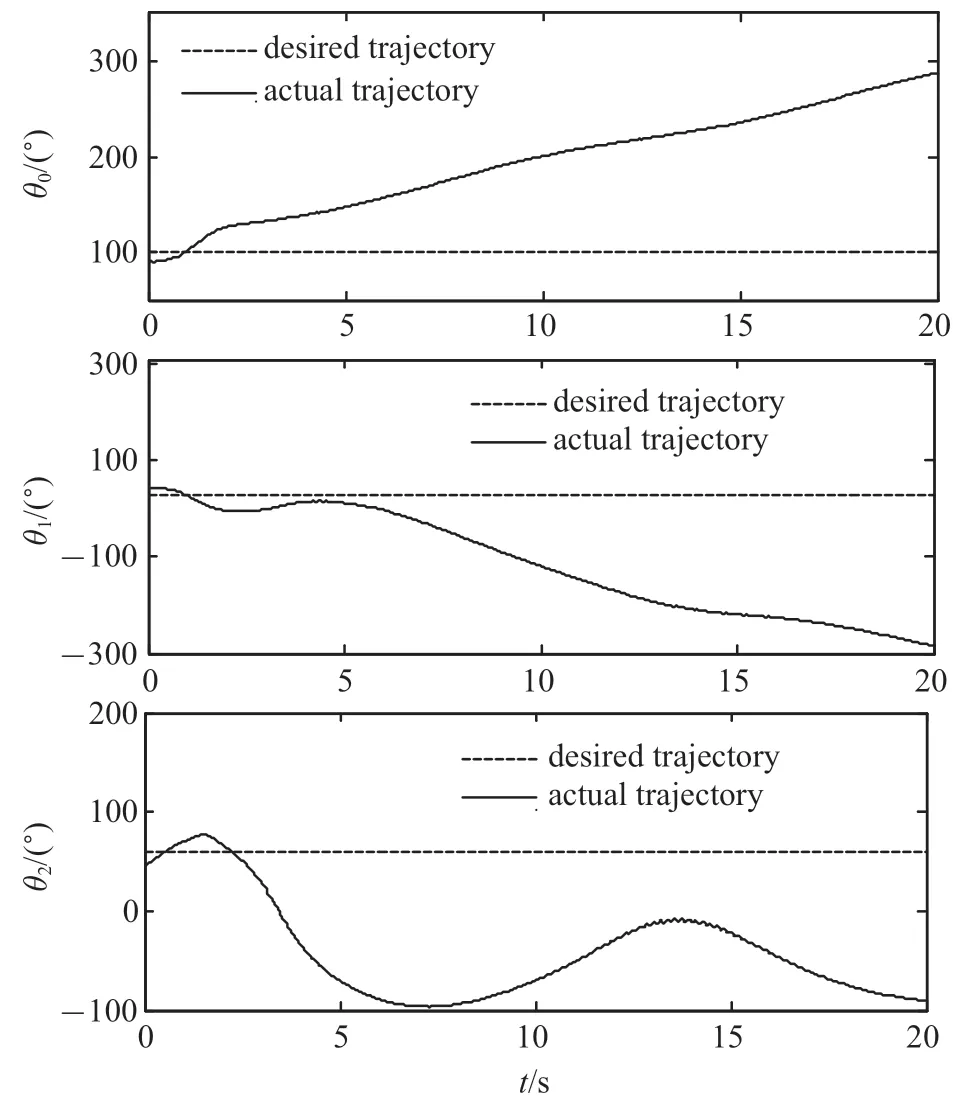
圖8 關閉快變控制器軌跡Fig.8 Trajectory without fast controller

5 結論

考慮空間機器人捕獲操作過程,其機械臂關節(jié)處將會受到巨大的碰撞沖擊力矩的影響.為了避免該沖擊力矩對關節(jié)電機造成破壞,本文設計了一種含RSEA 裝置的空間機器人,并提出了一種與之配合的適時開、關機控制策略.通過數(shù)值仿真可知,所提方案在捕獲接觸、碰撞階段,最大可減小63.2%關節(jié)所受碰撞沖擊力矩,最小也能減小49.9%,體現(xiàn)了良好的抗沖擊性能.在鎮(zhèn)定運動階段,借助奇異攝動技術,實現(xiàn)了對系統(tǒng)彈性振動的主動抑制,并保證了關機所受沖擊力矩限定在安全范圍內(nèi),從而避免了關節(jié)電機的過載、破壞.此外,所提基于動態(tài)面的自抗擾控制方案不僅簡化了計算過程;同時,還提高了系統(tǒng)的抗擾動性能,保證了鎮(zhèn)定運動的精確性和穩(wěn)定性.