飽和多孔地基與矩形板動(dòng)力相互作用的非軸對(duì)稱混合邊值問題1)

王立安 趙建昌 楊華中

(蘭州交通大學(xué)土木工程學(xué)院,蘭州 730070)

引言

地基板(梁)在動(dòng)力作用下的振動(dòng)彎曲問題在諸多工程領(lǐng)域有著重要的實(shí)踐應(yīng)用,如建筑物的筏板基礎(chǔ)、公路或市政道路的路面板、鐵路的軌道板以及飛機(jī)跑道等都可視為這類問題.以往研究中,通常采用線彈性、彈塑性或黏彈性本構(gòu)來(lái)模擬地基(如Winkler 地基),通過(guò)在板?土接觸面上添加彈簧支撐和阻尼黏壺來(lái)模擬接觸關(guān)系[1-6].眾所周知,土體是一種具有多相組成和骨架孔隙結(jié)構(gòu)的介質(zhì),采用彈(塑)性或黏彈性本構(gòu)來(lái)模擬土地基,是將土體視為單相介質(zhì),無(wú)法真實(shí)反映土體的力學(xué)性質(zhì).尤其在動(dòng)力作用下,土體中孔隙水的滲透作用以及固流耦合效應(yīng)對(duì)其動(dòng)力行為起到重要影響[7-10].而且采用添加彈簧支撐和黏壺的方式,使得計(jì)算結(jié)果完全依賴于地基彈性系數(shù)和阻尼比的選取,無(wú)法考慮板土接觸的真實(shí)情況.采用有限元分析地基板問題時(shí),同樣需要輸入地基彈性系數(shù)和阻尼比,而且傳統(tǒng)有限元軟件也沒有提供可模擬滲透和孔隙壓力的本構(gòu)單元,因此無(wú)法實(shí)現(xiàn)板土接觸分析的有限元模擬[11-14].何濤[15]基于任意拉格朗日?歐拉(ALE)有限元技術(shù),給出一種數(shù)值模擬固流耦合效應(yīng)的方法,但無(wú)法適用于土體.陳少林等[16-17]采用集中質(zhì)量顯式有限元方法,并結(jié)合透射邊界條件給出一種針對(duì)海洋地震工程流固耦合問題的統(tǒng)一計(jì)算框架.康建宏等[18]基于修正Darcy 模型,分析了多孔介質(zhì)內(nèi)黏彈性流體的熱對(duì)流問題.Biot[19-20]提出的多孔介質(zhì)理論為研究土體動(dòng)力響應(yīng)提供了理論基礎(chǔ).Zhang 等[21]給出一種分析飽和土與隧道結(jié)構(gòu)動(dòng)力相互作用的理論模型.陳少林等[22-23]基于Biot 理論對(duì)土?基礎(chǔ)?結(jié)構(gòu)系統(tǒng)在地震作用下的動(dòng)力響應(yīng)做了整體分析.

采用接觸分析法求解地基板問題時(shí),關(guān)鍵是接觸反力的確定.早期研究中,前蘇聯(lián)學(xué)者哥爾布諾夫波沙道夫[24]采用雙重冪級(jí)數(shù)展開給出彈性地基上矩形板的完全解析解,但這種解法形式太過(guò)復(fù)雜,并沒有在實(shí)踐中得到應(yīng)用.王春玲等[25-26]采用雙重三角級(jí)數(shù)展開的方法,分別給出了彈性地基和飽和多孔地基上矩形板動(dòng)力彎曲的解析解.這種方法與波沙道夫的方法相似,形式復(fù)雜存在收斂問題,而且無(wú)法求解復(fù)雜邊界條件的情形.一些學(xué)者將矩形板剛性化,假定接觸反力均勻分布,從而使問題簡(jiǎn)化為平面應(yīng)變問題進(jìn)行求解,對(duì)地基上剛性基礎(chǔ)的振動(dòng)問題做了解析研究[27-29].還有一些學(xué)者將矩形板視為無(wú)限大使問題簡(jiǎn)化為單一邊界問題從而進(jìn)行解析求解.孫璐等[30]給出彈性半空間上無(wú)限板的解析解;蔡袁強(qiáng)等[31-32]給出飽和多孔地基上無(wú)限大板的動(dòng)力彎曲解;張春麗等[33]給出各向異性彈性地基上無(wú)限大板的解析解.金波等[34-35]、陳龍珠等[36]利用Abel 變換給出了軸對(duì)稱混合邊值問題的求解方法,并由此得出飽和多孔地基上圓形板振動(dòng)彎曲的解析解.應(yīng)注意,對(duì)于圓形地基板的軸對(duì)稱問題,放在圓柱坐標(biāo)系下事實(shí)上是二維問題,其一般性將受到限制.此外,郭樹起[37]也給出了適用于軸對(duì)稱問題的邊界積分法.而對(duì)應(yīng)于矩形地基板的三維非軸對(duì)稱混合邊值問題的完全解析解,目前仍未見相關(guān)文獻(xiàn).

基于以上分析,本文考慮地基土的固流耦合效應(yīng)和孔隙水的滲透作用,基于Kirchhoff 理論和Biot 多孔介質(zhì)理論建立矩形板與飽和多孔地基動(dòng)力相互作用的計(jì)算模型.并且考慮了一種混合透水邊界,即板土接觸面為不透水界面,其余表面為透水界面.針對(duì)接觸面和非接觸面的混合邊值問題,通過(guò)雙重Fourier變換構(gòu)造出兩對(duì)二維對(duì)偶積分方程,并利用Hilbert正交化定理和Schmidt 法對(duì)二維對(duì)偶積分方程進(jìn)行求解,最終推導(dǎo)出板土系統(tǒng)在動(dòng)力作用下的位移和應(yīng)力解析式.通過(guò)數(shù)值計(jì)算,對(duì)飽和多孔地基上矩形板的振動(dòng)響應(yīng)和參數(shù)影響做了分析和討論.將計(jì)算結(jié)果與彈性地基上矩形板的振動(dòng)響應(yīng)進(jìn)行對(duì)比分析,總結(jié)出相關(guān)結(jié)論.

1 計(jì)算模型及基本方程求解

如圖1 所示,長(zhǎng)、寬分別為2la和2lb的矩形彈性板支撐在飽和多孔半空間表面.板長(zhǎng)方向?yàn)閤軸,板寬方向?yàn)閥軸,z軸指向地基.板中心作用有長(zhǎng)為2a寬為2b的簡(jiǎn)諧分布載荷.圖1(b)表示板?土接觸面為不透水界面,其余地表為透水界面.當(dāng)板?地基系統(tǒng)受到簡(jiǎn)諧載荷激勵(lì)時(shí),系統(tǒng)中各場(chǎng)量存在如下關(guān)系

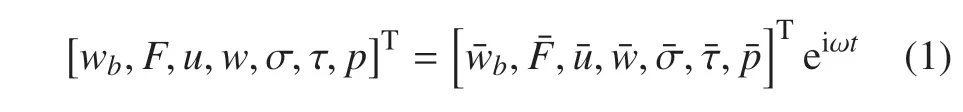
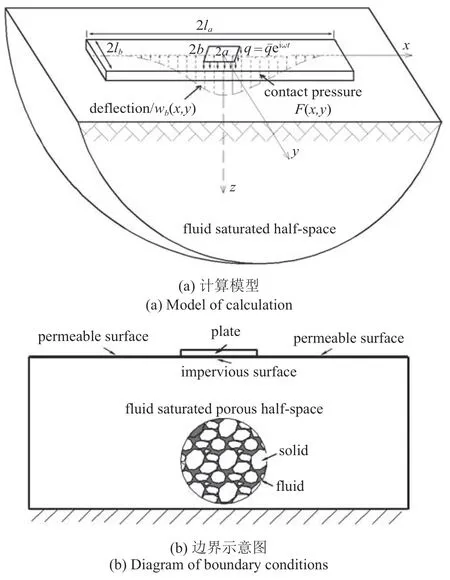
圖1 模型示意圖Fig.1 Diagram of calculation model

式中,wb為矩形板撓度,F為接觸反力,u為地基土骨架位移,w為孔隙水位移,σ 和τ 分別為土骨架正應(yīng)力和切應(yīng)力,p為孔隙水壓力.為對(duì)應(yīng)物理量的幅值.eiωt為諧和因子,ω 為角頻率,t為時(shí)間,i 為虛數(shù)單位.

1.1 矩形板基本方程求解

根據(jù)Kirchhoff 理論,矩形板撓曲方程表示為

式中,已根據(jù)式(1)將諧和因子eiωt約去;D為矩形板的撓曲剛度,?4=?4/(?x4)+2?4/(?x2?y2)+?4/(?y4);H()為Heaviside 階躍函數(shù).對(duì)x,y坐標(biāo)引入以下雙重Fourier 變換

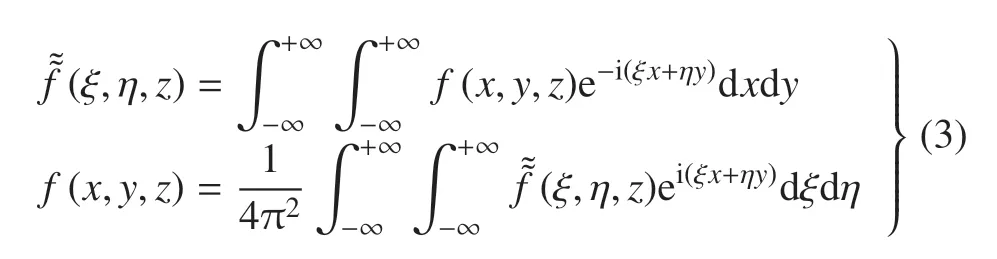
將式(3)用于式(2),解得

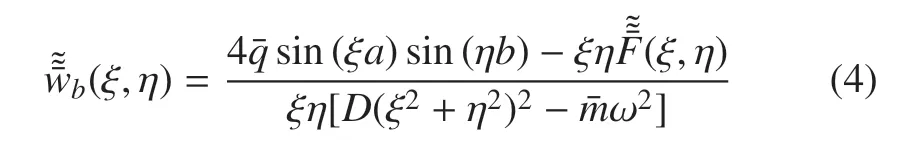
1.2 飽和多孔地基控制方程及求解

考慮孔隙流體壓縮性和流體與骨架的相對(duì)運(yùn)動(dòng),并忽略體力作用,Biot 飽和多孔介質(zhì)波動(dòng)方程寫為[19-23]

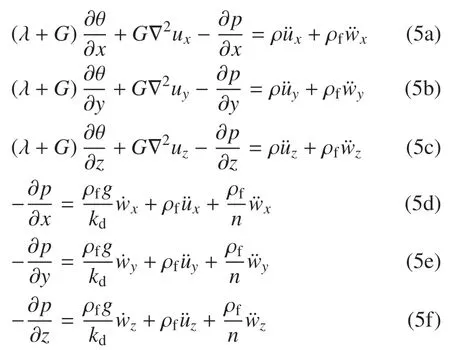
本構(gòu)方程

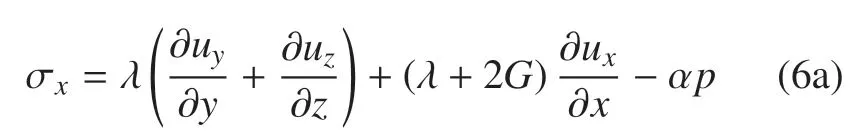
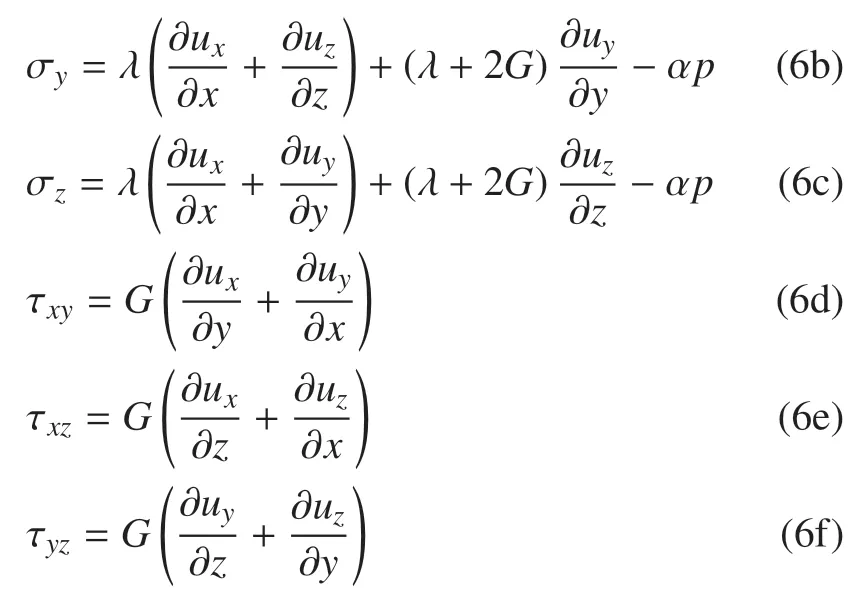
滲流連續(xù)方程

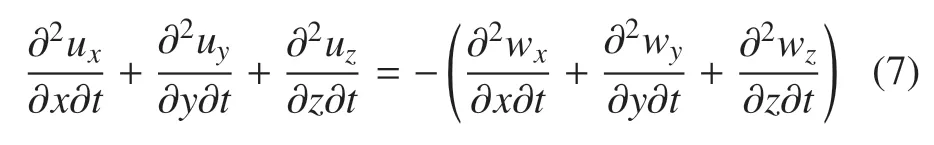
式中,θ=?ux/(?x)+?uy/(?y)+?uz/(?z)為固體骨架的體應(yīng)變;λ 和G為L(zhǎng)amb 常數(shù);ρ=nρf+(1 ?n)ρs為土體總質(zhì)量密度,其中ρs和ρf分別為固體顆粒和孔隙水的質(zhì)量密度;n為孔隙率;kd為滲透系數(shù);α 為表征固體顆粒壓縮性的常數(shù),當(dāng)考慮顆粒不可壓縮時(shí)α=1.

對(duì)式(5a)～式(5c)施以?(5a)/(?x)+?(5b)/(?y)+?(5c)/?z運(yùn)算,并考慮式(7),得到

對(duì)式(5d)～式(5f)施以?(5d)/(?x)+?(5e)/(?y)+?(5f)/(?z)運(yùn)算,得到

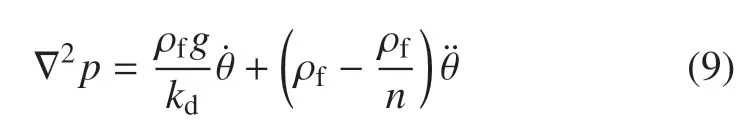
將式(8)代入式(9),得到

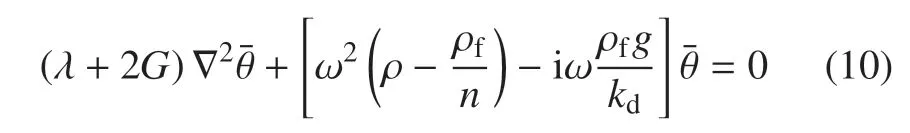
對(duì)式(10)進(jìn)行雙重Fourier 變換后得到

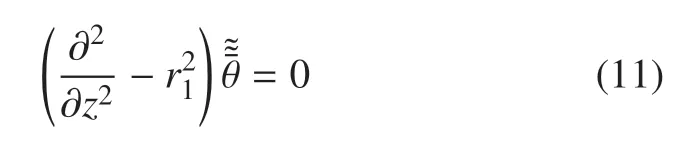
求解常微分方程(11),得到

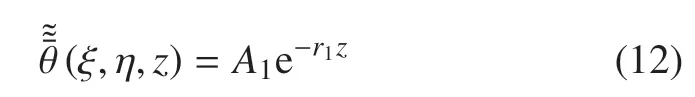
式中,r1=,取Re(r1)>0,以滿足波的輻射條件,Re表示取實(shí)部;φ=ρfω2/n+iωρfg/kd;M0=(ρω2?φ)/(λ+2G).

對(duì)式(9)做Fourier 變換,再將式(12)代入,即可求出孔隙壓力的變換域解

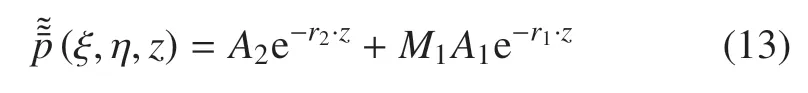
式中,r2=,M1=(ρfω2?φ)/M0.

由式(4d)～式(4f)可得到

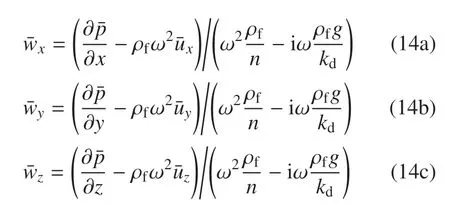
將式(14)分別代入式(5a)～式(5c),消去wx,wy和wz后進(jìn)行雙重Fourier 變換,得到

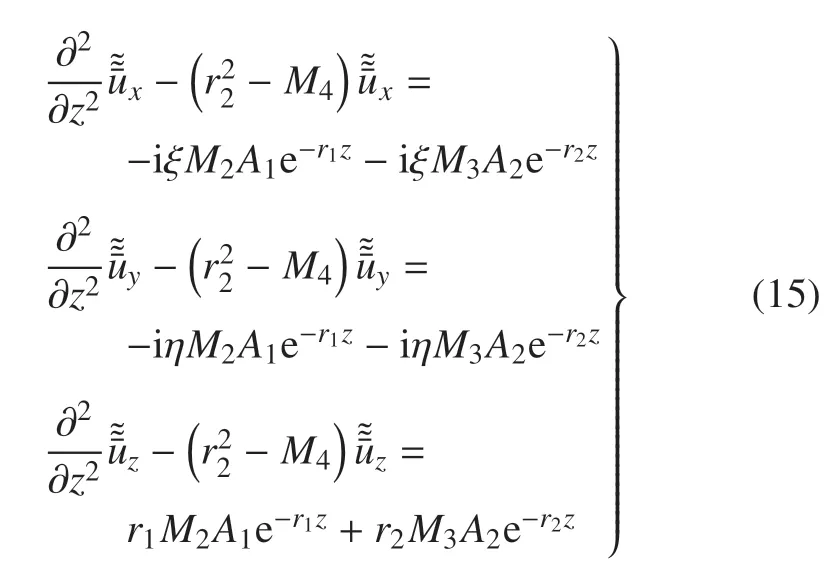
式中,M2=λ +G+M1M3,M3=ρfω2/? ?1,M4=,?=ρfω2/n?iωρfg/kd.

求解二階常微分方程組(15),得出位移解

式中,r3=,A1～A4為積分常量,由邊界條件確定;對(duì)本構(gòu)方程(6)做雙重Fourier 變換,并將位移解式(16a)～式(16c)代入,得到變換域的應(yīng)力解

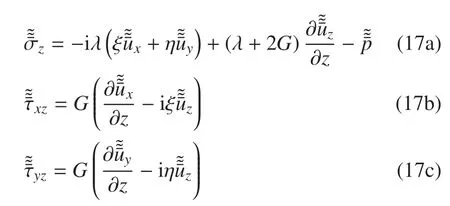
1.3 混合邊值問題求解

考慮矩形板與半空間表面光滑接觸,且不會(huì)發(fā)生脫離;并考慮板土接觸面為不透水邊界,其余表面為透水邊界.將接觸面區(qū)域(|x|≤la,|y|≤lb,z=0)記為?1,接觸面以外區(qū)域(|x|>la,|y|>lb,z=0)記為?2,則半空間表面z=0 處的邊界條件寫為

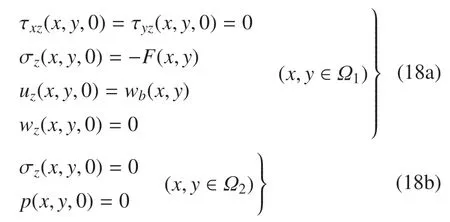
利用式(13)、式(17a)、式(18a)得出

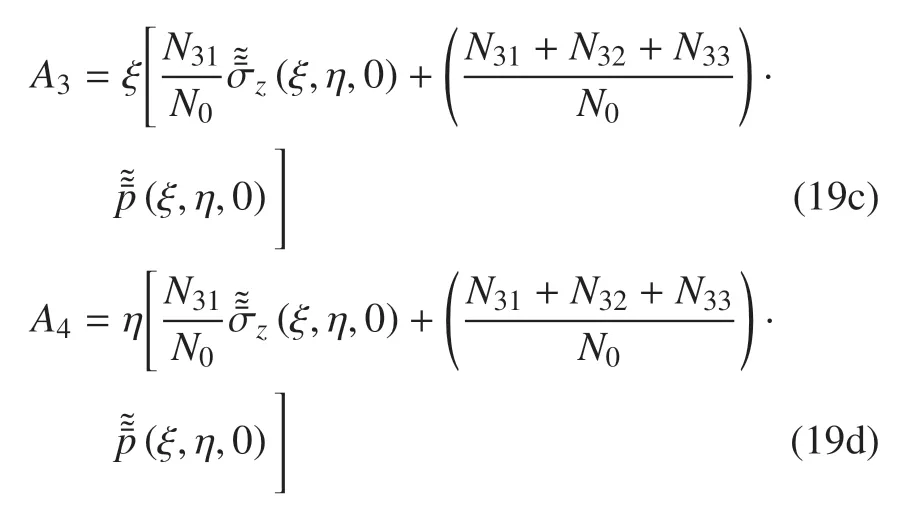
其中,N0及N11～N33見附錄.將式(19)代入式(4)、式(14)、式(16)中并進(jìn)行Fourier 變換,得到

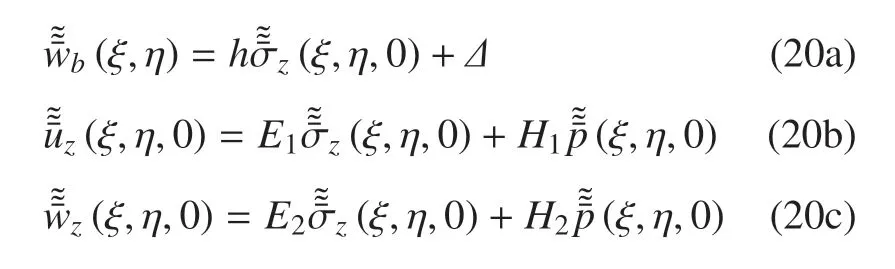
式中,h,Δ,E1,E2,H1,H2均為ξ 和η 的已函數(shù),形式見附錄.對(duì)式(20)做Fourier 逆變換,而后代入式(18a)和式(18b),整理出兩對(duì)二維對(duì)偶積分方程

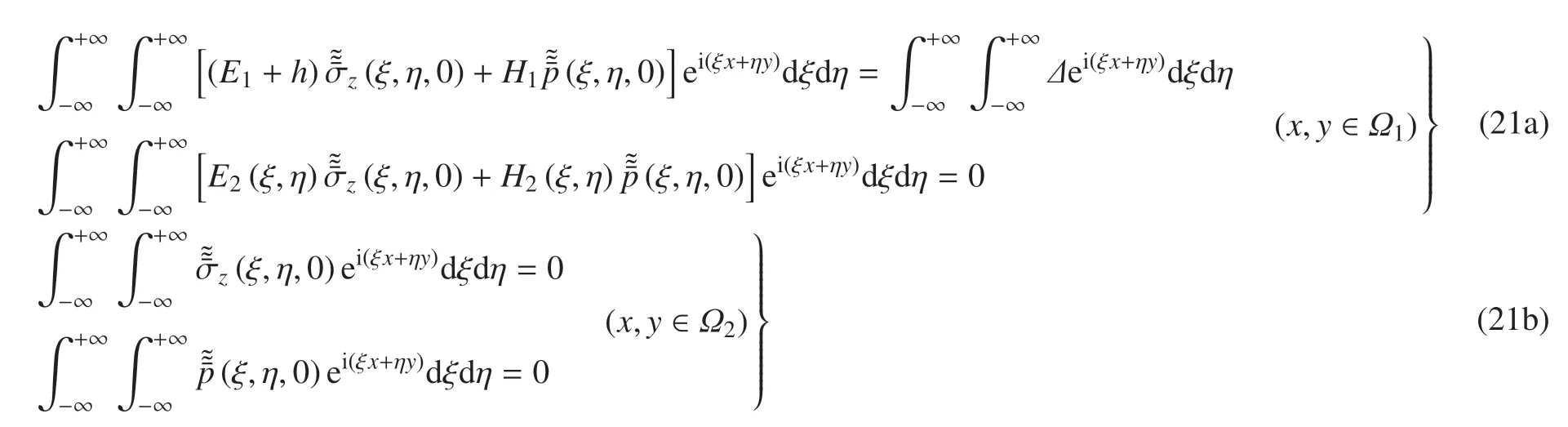
為求解對(duì)偶積分方程(21),根據(jù)Hilbert 正交化定理[38],利用Jacobi 正交多項(xiàng)式將積分核和展為如下級(jí)數(shù)形式[39]

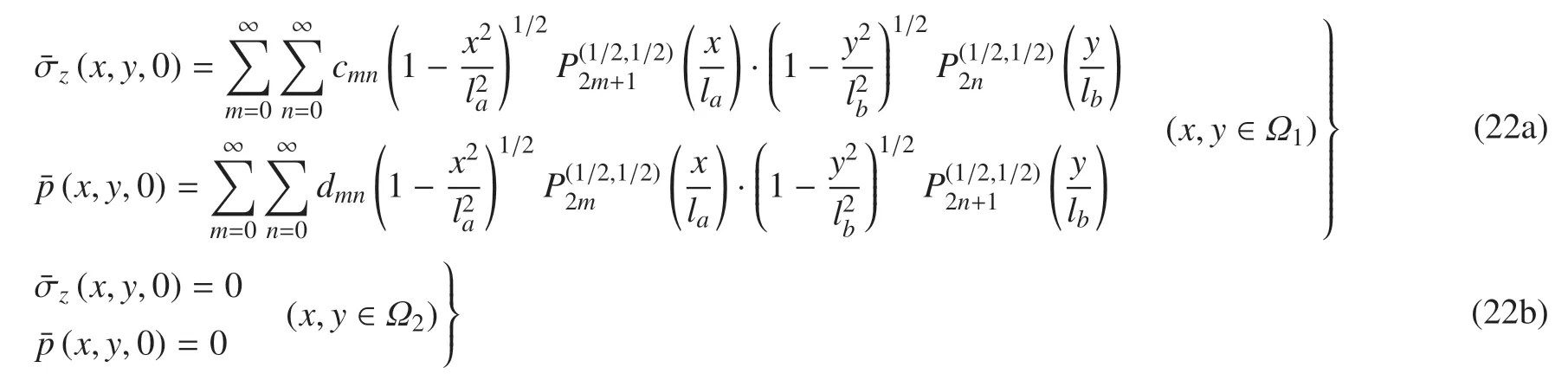
式中,cmn和dmn為未知系數(shù),為Jacobi 多項(xiàng)式.對(duì)式(22)進(jìn)行雙重Fourier 變換得到[40]

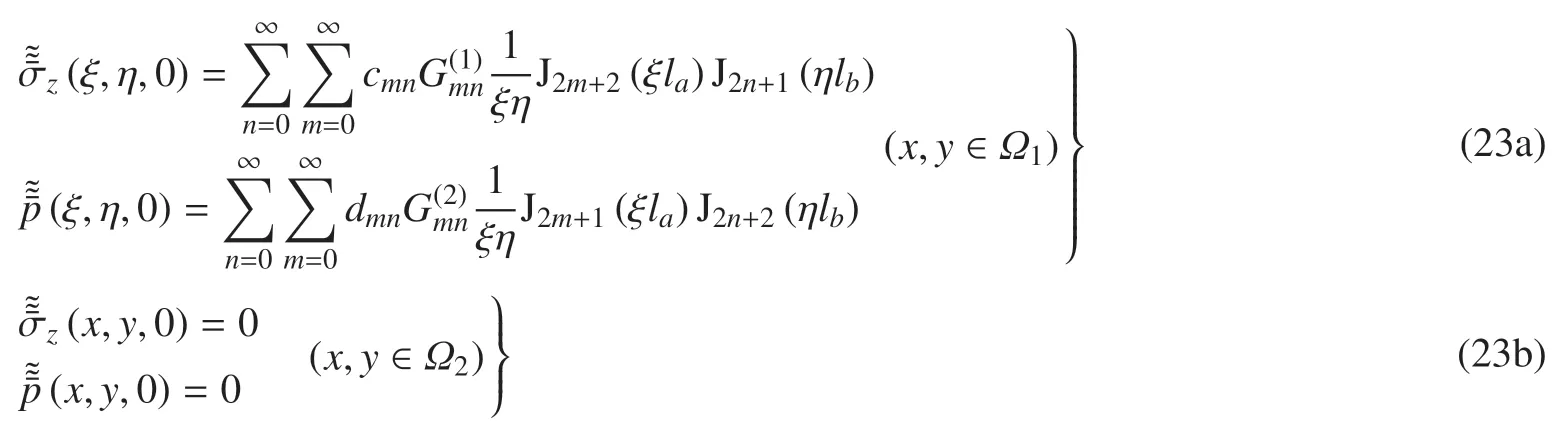
式中

其中,Γ(·),Jn(·)分別為Gamma 函數(shù)和Bessel 函數(shù).將式(23b)代入式(21),發(fā)現(xiàn)自動(dòng)滿足,將式(23b)代入式(21)后,則得到

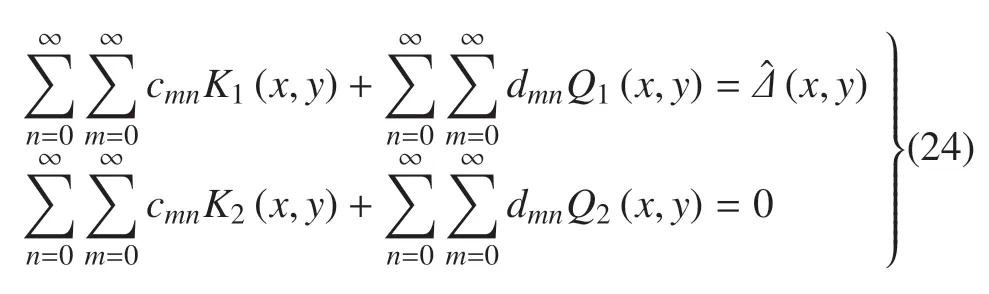
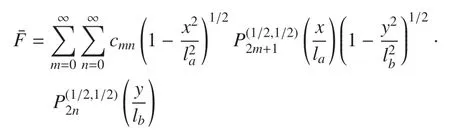
然后利用式(4)、式(16)、式(17)可分別得到矩形板和地基的位移和應(yīng)力解.

2 收斂性和正確性驗(yàn)證

首先進(jìn)行收斂性分析,以確定式(24)的級(jí)數(shù)項(xiàng)數(shù)m和n.為了便于比較,矩形板和地基的計(jì)算參數(shù)按文獻(xiàn)[20] 取值.取矩形板邊長(zhǎng)2la=2lb=4 m,板厚為0.2 m;板的泊松比為0.167,彈性模量Eb=34 300 MPa;地基泊松比為0.4,彈性模量Es=343 MPa;板中心作用均布載荷q=0.98 MPa.本文考慮的地基為兩相飽和多孔地基,所以還需補(bǔ)充土體孔隙率n=0.6,固體骨架密度ρs=2700 kg/m3、孔隙水密度ρf=1000 kg/m3,滲透系數(shù)kd=10?5m/s.通過(guò)MATLAB 編程,對(duì)本文推導(dǎo)結(jié)果進(jìn)行數(shù)值計(jì)算.圖2給出了矩形板中心點(diǎn)撓度幅值與網(wǎng)格數(shù)目m×n的關(guān)系曲線,圖中反映出本方法收斂速度很快,只需取m×n=16×16 個(gè)網(wǎng)格點(diǎn)足以得到收斂結(jié)果.

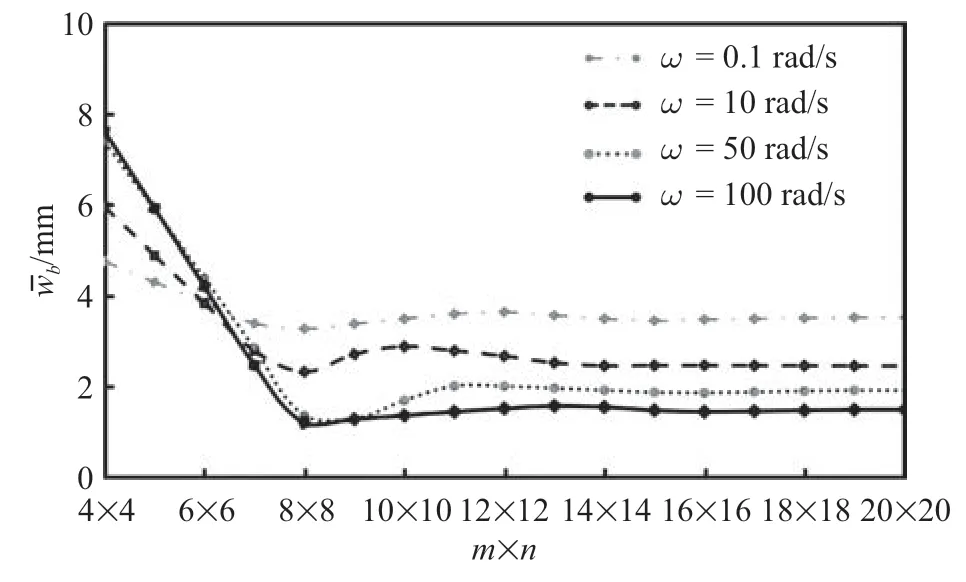
圖2 結(jié)果收斂性試算Fig.2 Verification of convergence

若取孔隙水密度ρf=0,代表地基中無(wú)水,則本文的地基模型退化為單一彈性地基,可與文獻(xiàn)[20]的結(jié)果進(jìn)行對(duì)應(yīng)比較.表1 列出了本文退化解與文獻(xiàn)解的對(duì)比,從表1 的對(duì)比結(jié)果可知,本文退化解與文獻(xiàn)[20] 很好吻合,由此驗(yàn)證了本文推導(dǎo)方法和數(shù)值計(jì)算程序的正確性.

表1 板中心撓度幅值及彎矩與文獻(xiàn)[20]對(duì)比Table 1 Comparison of calculation results

3 數(shù)值結(jié)果和討論

利用前文確定的計(jì)算參數(shù)和程序,對(duì)本文模型進(jìn)行數(shù)值計(jì)算圖3 給出了部分計(jì)算結(jié)果.圖4 為不同載荷激勵(lì)頻率下板中心位置的撓度時(shí)程曲線,為了進(jìn)行對(duì)比分析,在圖4(a)中繪出了對(duì)應(yīng)于彈性地基的計(jì)算結(jié)果.對(duì)比圖4(a)和圖4(b)可知,對(duì)于彈性地基,載荷激勵(lì)頻率的變化會(huì)造成板振動(dòng)頻率的變化,但不會(huì)改變其振動(dòng)幅值.而對(duì)于兩相飽和多孔地基,激勵(lì)頻率的變化不僅引起板振動(dòng)頻率的變化,其振動(dòng)幅值也發(fā)生大的變化.出現(xiàn)這一現(xiàn)象的機(jī)理可理解為,在載荷作用下,飽和多孔地基中固體骨架發(fā)生壓縮變形,孔隙受到擠壓,孔隙壓力進(jìn)而升高,而孔隙壓力會(huì)阻礙固體骨架進(jìn)一步變形.若孔隙中的水能及時(shí)滲透,則孔隙壓力將得以消散,這種阻礙效應(yīng)將不存在.試想一下,當(dāng)振動(dòng)頻率較高時(shí),孔隙水來(lái)不及滲透,則孔隙壓力持續(xù)升高,這種阻礙效應(yīng)將增大,地基將難以發(fā)生變形,地基剛性從而增大,板的撓曲幅值將隨之減小.

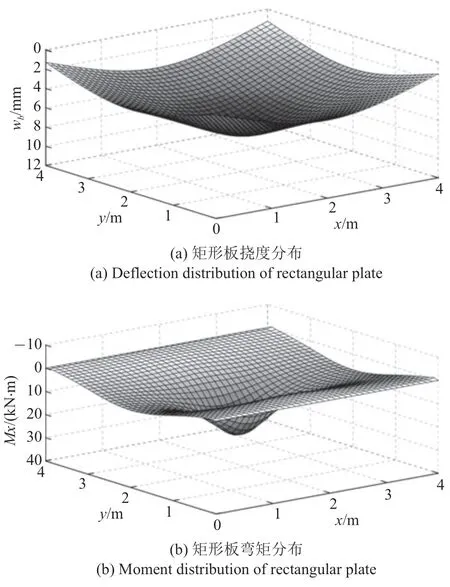
圖3 數(shù)值計(jì)算結(jié)果(ω=10 rad/s,t=0 s)Fig.3 Results of numerical computation with(ω=10 rad/s,t=0 s)

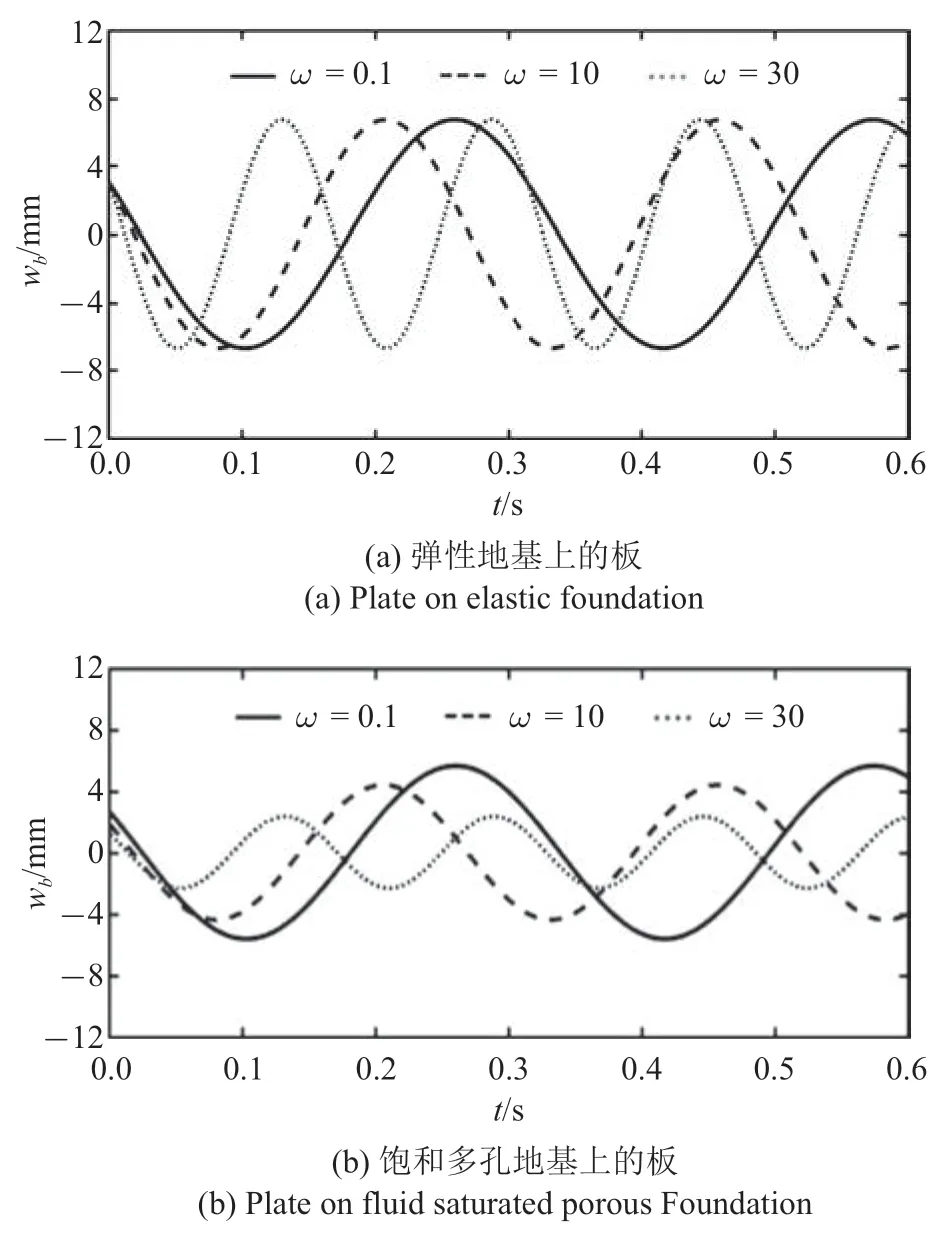
圖4 矩形板中心點(diǎn)撓度時(shí)程曲線Fig.4 Variation of deflection with time at the center of rectangular plate

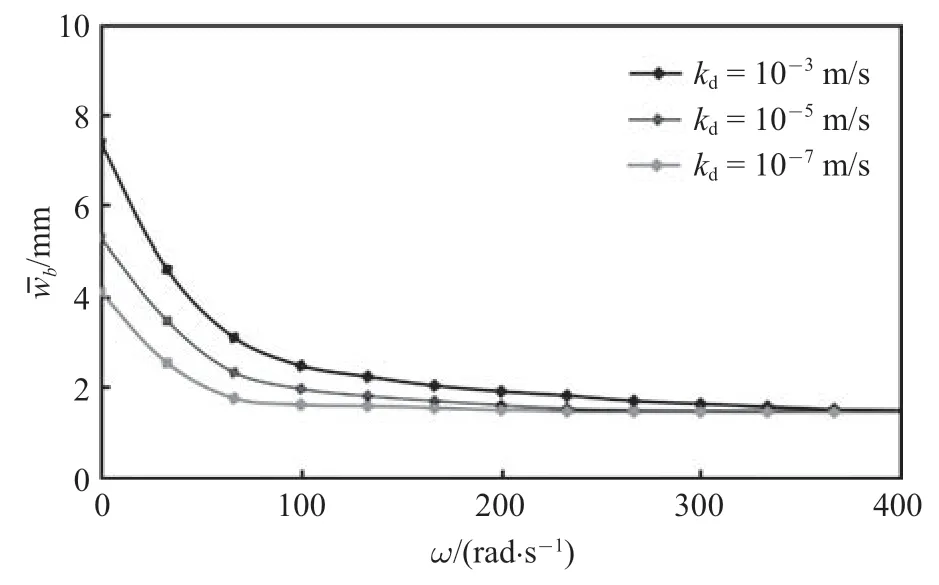
圖5 撓度幅值與激勵(lì)頻率關(guān)系圖Fig.5 Deflection amplitude relative to frequency

為進(jìn)一步考察飽和多孔地基上矩形板的振動(dòng)撓曲與激勵(lì)頻率的關(guān)系,圖5 給出激勵(lì)頻率與撓度幅值的關(guān)系曲線.分析圖5 可知,隨著激勵(lì)頻率增大,板的撓度幅值隨之減小.當(dāng)載荷激勵(lì)頻率達(dá)到極限時(shí),板的撓度幅值收斂于一固定值.圖中還反映出,撓度幅值的收斂速度與地基滲透系數(shù)有密切關(guān)系.為考察撓度幅值的最終收斂值,嘗試取地基滲透系數(shù)kd→0.計(jì)算發(fā)現(xiàn),激勵(lì)頻率達(dá)到極限時(shí),板的撓度幅值與地基滲透系數(shù)趨于0 時(shí)的結(jié)果近似相等(即wb|ω→∞≈wb|kd→0).這說(shuō)明,當(dāng)載荷激勵(lì)頻率達(dá)到極限時(shí),地基土體相當(dāng)于一個(gè)固流耦合的封閉系統(tǒng)(孔隙水不發(fā)生滲透).

圖6(a)和圖6(b)分別為矩形板中心點(diǎn)下0 m 和2 m 處地基土中孔壓隨時(shí)間的變化曲線.圖7(a)和圖7(b)為矩形板中心點(diǎn)下土體中固體骨架位移幅值U和孔隙壓力幅值P沿深度的分布曲線.圖中可以看出,隨著載荷激勵(lì)頻率增大,地基中固體骨架的水平方向和豎直方向位移幅值都隨之減小,位移響應(yīng)深度也隨即減小.但孔隙壓力幅值卻隨激勵(lì)頻率的增大而增大,這一結(jié)果也印證了前文的機(jī)理解釋.

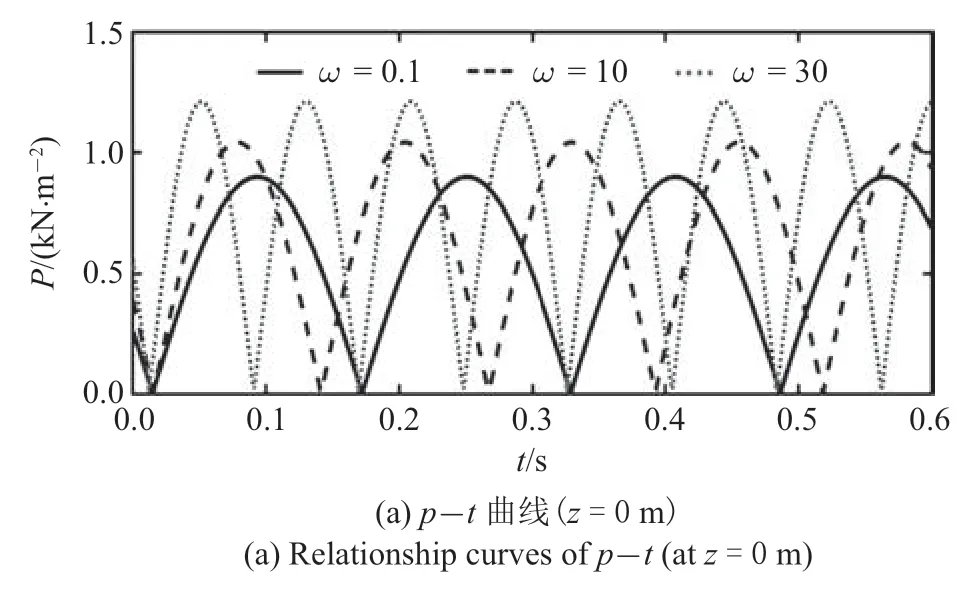
圖6 板中心點(diǎn)下地基中空隙壓力時(shí)程曲線Fig.6 Variation of pores pressure with time below the center point of rectangular plate

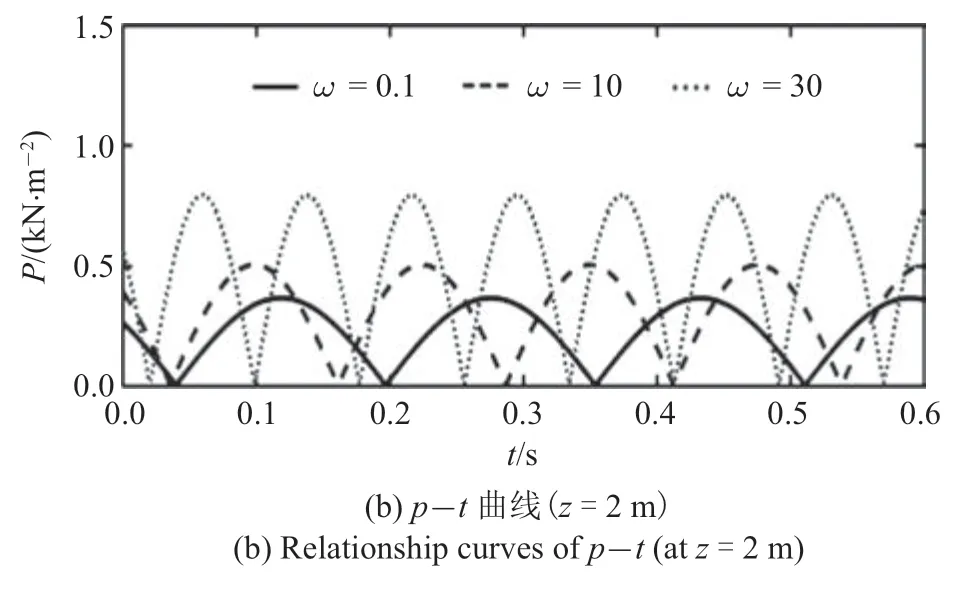
圖6 板中心點(diǎn)下地基中空隙壓力時(shí)程曲線(續(xù))Fig.6 Variation of pores pressure with time below the center point of rectangular plate(continued)

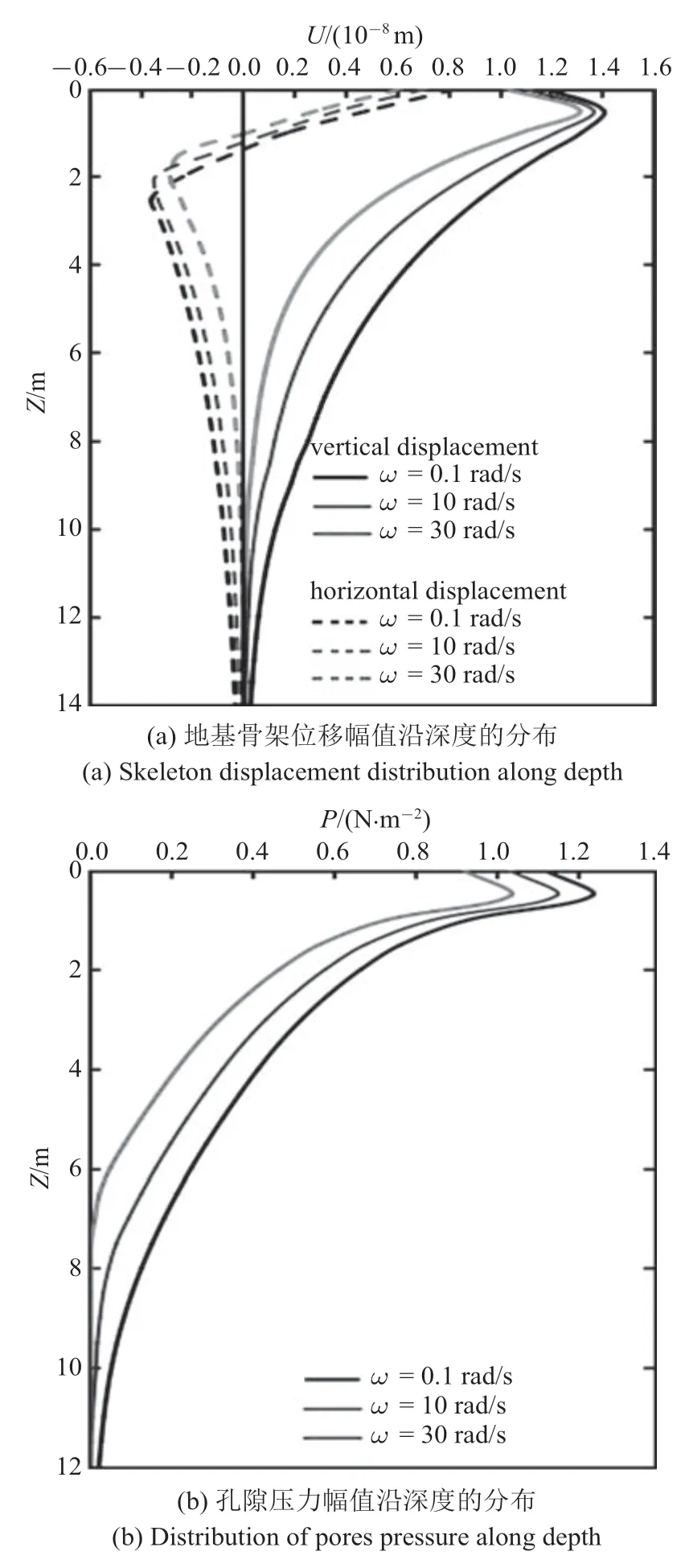
圖7 地基中變形和孔隙壓力Fig.7 Displacement and pore pressure of foundation

圖8 為激勵(lì)頻率ω=30 rad/s 時(shí),土?板模量比(Es/Eb)與板的撓度幅值的關(guān)系.圖中可看出,Es/Eb取值越小,地基土相對(duì)于板越松軟,板的變形越大.圖7(b)比較了相同模量比取值下彈性地基與飽和多孔地基上的板撓曲變形,進(jìn)一步說(shuō)明了飽和多孔地基中孔隙壓力對(duì)地基剛性的貢獻(xiàn).

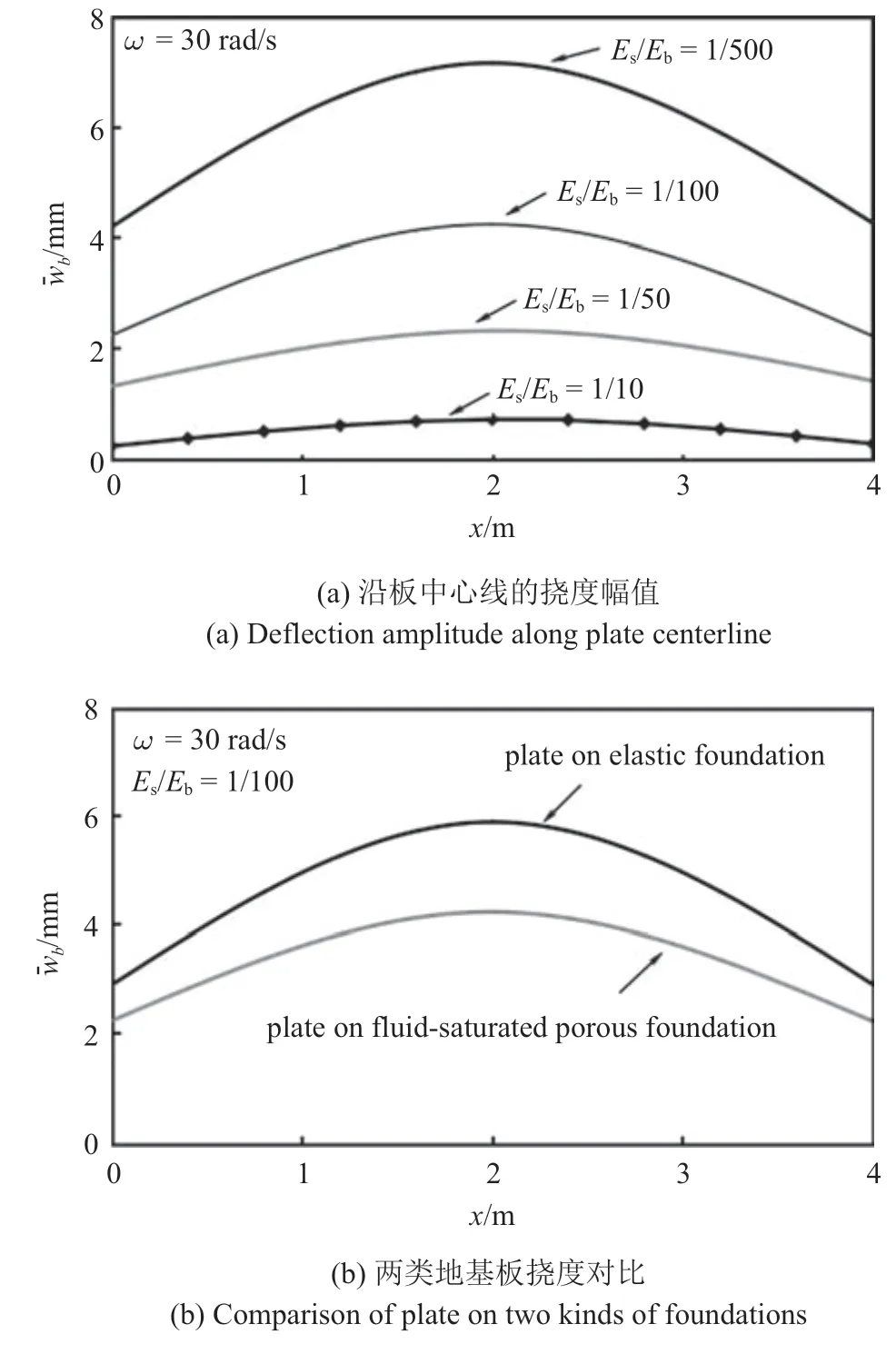
圖8 模量比(Es/Eb)對(duì)地基板撓度的影響Fig.8 Influence of modulus ratio on plate deflection

4 結(jié)論

本文建立了具有混合透水邊界的板土接觸模型,利用Hilbert 定理和Schmidt 法解決了非軸對(duì)稱混合邊值問題的求解,從而得出飽和多孔地基上矩形板振動(dòng)彎曲的解析解.通過(guò)數(shù)值計(jì)算,發(fā)現(xiàn)飽和多孔地基中由于孔隙壓力的作用,地基剛性將隨激勵(lì)頻率的增大而提高.而地基板的振動(dòng)變形將隨載荷激勵(lì)頻率的增大而減小.本文提出的非軸對(duì)稱混合邊值問題的解析法,具有一般性,可廣泛應(yīng)用于復(fù)雜接觸問題和多場(chǎng)耦合問題的求解.

附 錄