地方師范院校《拓撲學》課程教學內容優化探討

覃城阜

摘 要 《點集拓撲》是數學專業的一門重要基礎課，其對培養學生的抽象思維能力和邏輯推理能力有著重要的作用。本文在教學實踐的基礎上對《拓撲學》教學內容的優化進行了探討。

關鍵詞 點集拓撲 教學內容 優化

0引言

數學是自然科學的語言，隨著互聯網技術的發展，數學成為對于一個國家的發展至關重要因素。歷史上在數學研究處于領先的國家，在國家綜合實力上也往往處于領先地位。現如今，“發達國家常常把保持數學領先地位作為他們的戰略需求”。美國數學家 M·克萊因把數學對于現代社會的重要性描述為“一個時代的總的特征在很大程度上與這個時代的數學活動密切相關”。數學對于國家實力的提高，對于國家在高科技領域處于領先地位，對于國民素質的提高都有著重要的作用。李克強總理曾指出 “數學特別是理論數學是我國科學研究的重要基礎” ，“無論是人工智能還是量子通信等，都需要數學、物理等基礎學科作有力支撐。我們之所以缺乏重大原創性科研成果，‘卡脖子就卡在基礎學科上”。拓撲學作為數學學科的一門重要基礎課，可以說是集數學抽象和邏輯推理之大成者，它從概念出發演繹出一套邏輯體系，是培養學生數學抽象能力和邏輯推理能力的一門重要課程。

正是基于數學對于當今社會發的重要性，教育部在《普通高中課程方案和語文等課程標準》提出全面培養學生的“核心素養”，指出“各個學科必須達成正確價值觀念、必備品格和關鍵能力，要更多的關注學科思想、思維方式等”。另外，2018年教育部發布了《普通高等學校本科專業類國家教育質量標準》（以下簡稱標準），其中對數學與應用數學專業課標準給出了兩套選擇方案：一是把數學分析、高等代數、解析幾何、概率論、數學建模（含實驗）、常微分方程、實變函數、復變函數、抽象代數、偏微分方程、數理統計、計算方法、微分幾何、泛函分析、拓撲學作為核心課程，一是將專業知識按照課程分為專業基礎課、專業必修課和專業選修課，其中專業基礎課程為：數學分析、高等代數、解析幾何、概率統計、數學建模;專業必修課各校根據不同的培養方向，從下列三組課程的至少兩組中選定至少六門課程作為本校數學與應用數學專業的主干課程：

A組：抽象代數，微分幾何，拓撲學，初等數論;

B組：常微分方程，數學物理方程，復變函數，實變函數，泛函分析;

C組：數理統計，隨機過程，離散數學，數值分析，運籌學，控制論基礎。

我們注意到了這樣一個細節，在數學與應用數學專業課程國家質量標準制定的過程中，專家就拓撲學課程的課時安排給出如下建議：綜合性大學的拓撲學課程為64學時，而師范類專業是72學時。我們認為這樣的考慮是不無道理的，也顯示了拓撲學對師范專業學生的抽象能力和邏輯推理能力訓練起著重要的作用。

在核心素養理念的指導下，近年來全國的高考數學題目也越來越多趨向于考察學生的能力素養。2018年北京市高考數學理科卷最后一道題， 就是給出一個定義，讓學生從給定的定義出發去推導出相關的結論。

（2018年高考數學理科卷第20題）

設n為正整數，集合，，對于集合A中的任意元素和，記

（Ⅰ）當時，若，，求和的值;

（Ⅱ）當時，設B是A的子集，且滿足：對于B中的任意元素，，當、相同時，是奇數;當，不同時，是偶數。求集合B中元素個數的最大值;

（Ⅲ）給定不小于2的n，設B是A的子集，且滿足：對于B中的任意兩個不同的元素，，，寫出一個集合B，使其元素個數最多，并說明理由。

這道題要求學生要有較高的數學素養，基本上沒有直接用到高中數學所需的知識，而是要求學生能夠根據定義出發進行推理求證。因此，作為培養中學教師主力軍的地方高師院校數學與應用數學專業有必要開設拓撲學課程，充分的訓練學生的邏輯推理能力和抽象能力，這樣才能夠滿足基礎教育對教師專業能力的需求。

1地方高師院校中《點集拓撲》課程的設置現狀

就廣西區內師范院校數學與應用數學專業而言，由于總學分的減少，加上作為師范類的學生需要開設一定量的教師教育類課程，近年來，百色學院、河池學院、廣西民族師范學院、玉林師范學院、北部灣大學等地方高師院校數學與應用數學師范專業都不再開設拓撲學課程。南寧師范大學2016級之前的學生都是將拓撲學作為專業限選課開設;自2016級起，由于師范專業認證等工作的需要，從全局角度出發決定不再開設《拓撲學》課程。但是在實踐過程中我們發現，這對培養學生的數學抽象能力是非常不利的，對于部分考研學生而言沒有經過《拓撲學》課程的訓練對于他們迅速的適應研究生階段的學習也是不利的。因此，從2017 級又將拓撲學作為專業選修課程開設，只要選課學生人數達到30 人就開課。

對于拓撲學課程的教學安排，以使用熊金城主編的《點集拓撲講義》作為參考，我們通過網絡在線的方式對地方高師院校拓撲學課程相關資料進行收集。經過歸納整理，發現主要有如下三種教學方案。第一種方案中該課程占2學分，共36課時，主要講授第一至第三章及第五章的內容。對于地方高師院校而言，在學分有限的情況下，這樣的安排也是較為合理的。第二種方案中該課程占3個學分（按照規定，每個學分對于16-18學時），總計48-54學時，具體教學內容為第一章至第七章。第三種方案也是3個學分，但教學內容上有所不同，增加了“基本群及其應用”這一部分內容。采用第一、第三種方案的院校不多，大多數院校是采用第二種方案。

2點集拓撲課程具體教學建議

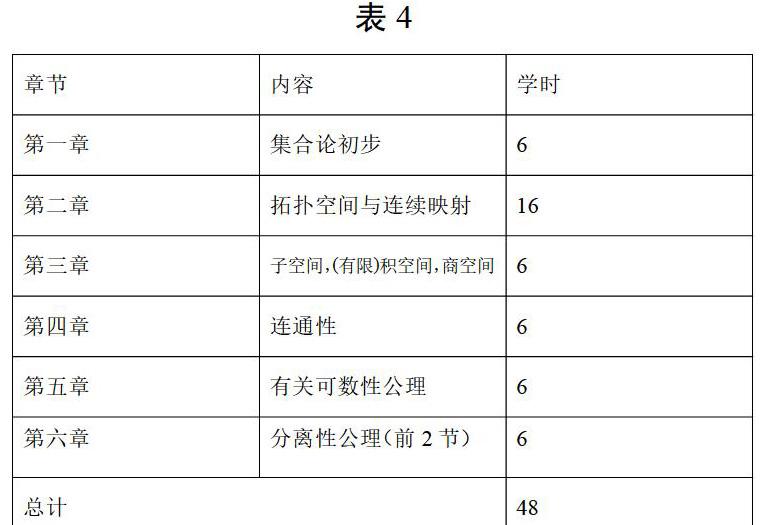
據我們對拓撲學課程的教學經驗來看，若按3學分計，每學分16課時，則總計有48課時。按照我校一直以來的教學計劃，授課內容為第一章至第七章。就學生的基礎及接受能力而言，48課時講完七章的內容非常緊張，而且教學效果不好，很多學生對教材的內容理解不到位，導致大部分學生對點集拓撲這門課程具有恐懼感，并把這種恐懼感傳給下一個年級的學生，這樣使得很多學生還沒有開始接上課就主觀排斥該課程。因此，我們認為目前地方高師院校開設這門課程，在學分無法增加的情況下，應適當減少教學內容，即將第六章部分內容和第七章全部內容舍棄，只講第一章到第六章第二節。具體章節課時安排如下。

在上述教學安排中， 我們將三分之一以上的課時安排在了第二章，主要原因有兩個：一是第二章本身的內容比較多;二是第二章是整個點集拓撲的基礎，這里有大量的定義和定理需要學生去理解和把握。可以說，如果學生能夠對第二章有比較好的把握則于后續章節的學習會相對容易很多。因此，我們對第二章的教學提出如下幾點建議。

2.1充分利用學生已有的知識加強學生知識的遷移

在第二章的教學中，我們要充分的挖掘學生已有的知識貯備，幫助學生建立已有知識與新知識之間聯系的橋梁，使得新知識通過學生已有知識順利內化， 這樣使得學生對抽象知識的理解和把握更加到位。

在熊金城編寫的教材《點集拓撲講義》中，拓撲空間與連續映射就是通過介紹度量空間中的具體情況來引入的。在后續的內容如鄰域、聚點、序列收斂等定義及相關內容的介紹中都可以做這樣的安排，提升學生學習的信心。如在講授序列收斂的定義時，可以先回顧數學分析中數列收斂的定義：

定義1：設是數列，a為定數。若對任意的正數， 都存在正整數N，使得當時有：，則稱數列收斂于a。

由于與是等價的;另外，由的任意性我們可以知道也是任意的。于是我們可以將上面的數列收斂的定義換一種方式來寫，得到如下定義1。

定義1：設是數列，為定數。若對任意的鄰域，都存在正整數N，使得當時有，則稱數列收斂于。

此時，引導學生將定義的本質抽出來，就可以自然的引出一般拓撲空間中的序列收斂的定義。

定義2：設是拓撲空間中的序列，為中的元素。若對任意的鄰域，都存在正整數，使得當時有，則稱數列收斂于。

這樣的教學能夠較為自然的引出定義定理，使得教學過程自然和諧。同時，通過對學生所熟悉的內容進行回顧鋪墊之后，學生更容易去理解定義定理，也更容易將知識內化，教學效果自然不同。

另外，我們也要引導學習對已有知識進行類比，從而把握新的知識，這樣更有助于幫助學生去理解和記憶新知識。如在講解”拓撲基“的概念的時候，可以將《高等代數》中的”基“的概念拿來對比：線性空間V中的所有向量都可以由基表示出來，并且要驗證某種保持線性關系的性質對于V中的所有向量成立，我們只需要驗證對于基中的向量成立即可。有了這個作為鋪墊，我們就可以討論拓撲空間中的基的定義及其作用，學生也能夠比較容易去理解和把握。

2.2通過具體的例子來加強學生的感性認識

實數空間中所具有的很多結論在一般拓撲空間中是不成立的，在授課過程中可以通過適當具體的例子來說明，讓學生增加感性的認識，從而加深對一般拓撲空間的性質的認識。如在實數空間中收斂序列的極限一定是唯一的，而從一般拓撲空間序列收斂的定義可以看出序列收斂不一定是唯一，我們可以通過如下的例子來說明。

同時，通過這個例子，可以知道序列收斂與否是嚴格依賴于拓撲的定義，同樣的序列在不同的拓撲空間中是否收斂、收斂值是什么都由拓撲來決定的。這就要求學生不能按照已有的知識推出結論，而是根據特定的拓撲，嚴格依據定義進行推導。這樣對學生的推理能力的訓練是非常有效的。

另外，第二章除了直接定義拓撲之外，還通過鄰域系、閉包運算、“基”、“子基”等四個角度定義了拓撲。這些定義都比較抽象而且證明也比較復雜。在講完相關證明之后，如果能夠給出一個具體的例子讓學生直接去驗證，則會大大加強學生的感性認識，更有利于學生掌握其本質。如在閉包運中，我們可以給出如下的例子讓學生去驗證。

拓撲學是一門抽象程度較高的課程，對于訓練學生的數學抽象和邏輯推理能力是十分有效的，在科學技術發展越來越依賴數學的今天，經濟社會發展需要更多具有較高數學素養的人才。基礎教育是培養人的數學素養的重要階段，因此作為培養基礎教育數學教師主力軍的地方高師院校開設拓撲學課程是十分有必要的，同時，在教學過程中可以根據學生的數學基地等方面對教學內容進行適當優化。

參考文獻

[1] 張恭慶.數學與國家實力（上）[DB/OL].http：//www.cms.org.cn/news/118.html， 2015.

[2] 李克強.為何反復強調數學等基礎學科的重要性[DB/OL].http：//www.gov.cn/xinwen/2018-01/04/content_5253247.htm.

[3] 普通高中課程方案和語文等課程標準[DB/OL].http：//www.moe.gov.cn/srcsite/A26/s8001/201801/t20180115_324647.html.

[4] 教育部高等學校教學指導委員會.普通高等學校本科專業類教學質量國家標準[M].北京：高等教育出版社，2018.

[5]林慶南.點集拓撲學教學探索[J].廣西教育學院學報，2011（03）：123-125.

[6]張亞圖.點集拓撲學中的數學抽象方法[J].江蘇教育學院學報，2002，19（03）：5-7.