環形陰極宏觀場增強因子計算研究

黃種亮，徐啟福，來定國，邱孟通

(1.清華大學 工程物理系，北京 100084；2.粒子技術與輻射成像教育部重點實驗室，北京 100084；3.西北核技術研究院 強脈沖輻射環境模擬與效應國家重點實驗室，陜西 西安 710024)

陰極是脈沖硬X射線負載、強流電子束二極管及高功率微波系統中的關鍵部件，常用的陰極結構有平面陰極、半球頭陰極、針狀陰極和環形陰極等[1-3]。大量研究表明提高陰極表面電場上升速率能減弱電子微發射點的屏蔽作用，有效提高陰極電子發射均勻性。宏觀場增強型陰極可在加載功率源參數不變的情況下，提高陰極表面電場上升速率，改善電子發射情況[4-6]。環形陰極是一種典型的場增強型陰極，被廣泛應用于高功率脈沖技術領域。在串級二極管和軔致輻射反射三極管中，環形陰極提供強流電子束用于打靶產生脈沖硬X射線輻射場，從而開展輻射效應的實驗研究[7-8]。高功率微波系統中，使用環形陰極設計O型微波產生器件，實現較高的微波轉換率[9-11]。因此，對環形陰極的宏觀場增強因子開展計算研究具有重要意義。陰極宏觀場增強因子不僅與陰極的形狀有關，而且與負載整體尺寸和結構有關。文獻[12-16]對平板陰極、半球頭陰極和同軸筒狀陰極的宏觀場增強因子開展了一些研究，獲得了針對特定結構參數的宏觀場增強因子估算公式，對陰極的設計優化具有一定借鑒意義。本文針對環形陰極的宏觀場增強因子進行理論計算研究。

1 細圓環的電勢分布求解

假設空間中有一理想的均勻帶電細圓環，其位于xOy平面上，圓心位于原點O，半徑為r，線電荷密度為λ，計算圓環對空間中任意位置處的電勢貢獻。由于圓環的電勢分布圍繞z軸存在軸對稱，所以只需考察xOz平面上任意點的電勢分布，計算坐標系如圖1所示。

定義無窮遠處的電勢為0，取細圓環上一無限小的微元rdθ，則該微元對空間中P(x,z)的電勢貢獻UP為：

(1)

其中，ε0為真空介電常數。

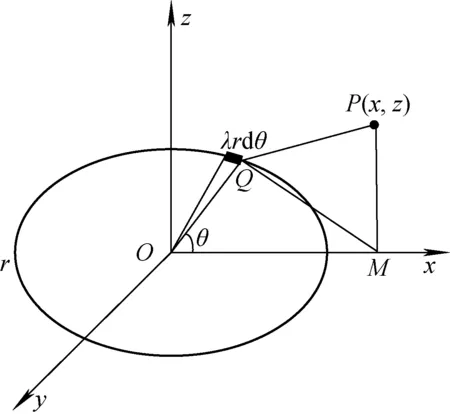
圖1 均勻帶電細圓環電勢分布計算Fig.1 Electric potential computation of uniformly charged ring

根據電勢疊加原理，細圓環對空間中任意點P(x,z)的電勢貢獻為所有微元的電勢貢獻總和。將式(1)在整個圓環上進行積分，求得圓環對P點的電勢貢獻為：

(2)

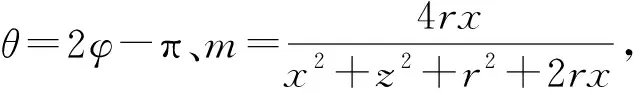
(3)

其中，K(m)為第一類橢圓積分。

2 環形陰極場分布求解

在環形陰極二極管中，加載到陰陽極間隙的電壓為V0，假設陰極厚度近似為0，陰極內徑為Ri，外徑為Ro，電勢為-V0，陽極近似無窮大，電勢為0，陰陽極間隙為d。由鏡像法可知，存在鏡像陰極與原陰極關于陽極對稱，其電勢為V0，陰陽極間電勢分布可通過求解兩陰極間的電勢分布獲得。由于空間電勢的軸對稱分布，可將三維問題簡化為xOz平面上的二維問題(圖2)。

圖2 二極管電場強度分布計算模型Fig.2 Computation model for electric field intensity distribution of diode

電子發射前，空間中任意位置的電勢本質上由陰極表面的電荷分布決定，因此電勢問題轉化為求解陰極表面的電荷分布。將陰極均勻分為2N個細圓環，上下各N個。當N足夠大時可認為每個細圓環上電荷均勻分布，第i個圓環的線電荷密度為λi，圓環半徑為ri，圓環寬度中心位置的坐標為(xi,zi)。由式(3)可知，第i個圓環在空間任意位置P(x,z)的電勢貢獻UPi為：

(4)

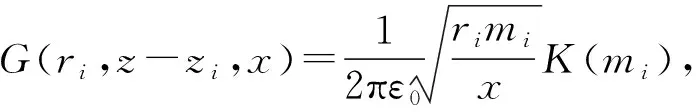
UPi(x,z)=G(ri,z-zi,x)λi

(5)

由電勢疊加原理可知，xOz平面內任一位置處的電勢可由2N個細圓環在該處電勢疊加求得：

(6)

設第i個圓環寬度中心位置的電勢為Vi，由式(6)可得：

(7)

令Gi,j=G(ri,zi-zj,xi)，可得到2N個線性方程：

(8)

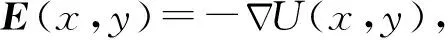
以下就特定算例進行計算，取Ri=0.055 m、Ro=0.06 m、d=0.05 m、V0=1 V、N=1 000，用Matlab編程求解式(8)獲得陰極表面電荷密度分布(圖3)，進而求出陰陽極間隙中電勢和電場強度空間分布，如圖4所示。由圖3可知，陰極表面的電荷強烈集中在陰極環的兩個棱邊上，陰極環正中間位置處的電荷密度最小，最大電荷密度是最小電荷密度的16倍。由圖4可知，陰陽極間隙中，陰極環內外棱邊附近的等勢線分布最為密集，對應棱邊附近的電場最強，與陰極表面電荷密度分布情況相符合。

圖3 電荷密度分布Fig.3 Distribution of charge density

圖4 電勢和電場強度分布Fig.4 Distribution of potential and electric field intensity

3 宏觀場增強因子計算研究

定義平均宏觀場增強因子βE為：

(9)

從式(9)可知，求解宏觀場增強因子需已知陰極表面電場分布，因此采用理論模型計算出陰極表面電場分布，并將其與Ansoft軟件模擬結果進行比較(圖5)。從圖5可知，理論模型計算結果與數值模擬結果符合得較好，且陰極表面電場分布強烈集中于陰極環的棱邊，與圖3、4所示分布規律相符。其中，最大電場是最小電場的7.2倍。

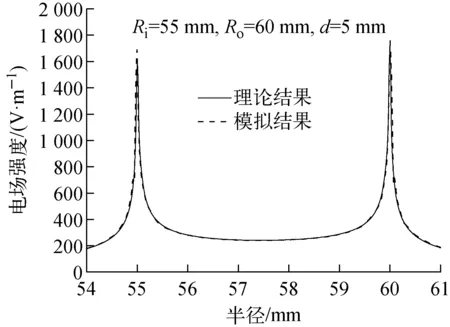
圖5 環形陰極表面電場分布Fig.5 Electric field distribution of annulus cathode surface

改變環形陰極二極管的結構參數，計算出不同結構參數對應的宏觀場增強因子，研究宏觀場增強因子隨結構參數的變化關系，結果如圖6所示。由圖6可知：1) 宏觀場增強因子由陰陽極間隙與陰極環寬之比(d/w)所決定，與陰極半徑無關，當陰極半徑不同，但d/w相同時，則所對應的宏觀場增強因子也相同；2) 宏觀場增強因子βE與d/w呈線性正相關，其擬合公式可表示為：

(10)

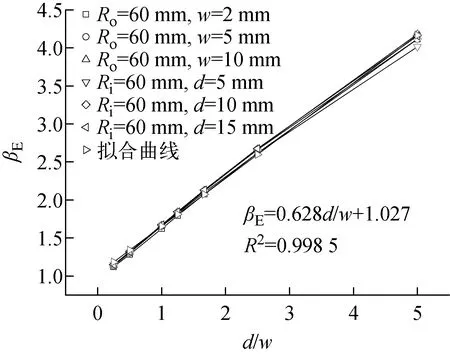
圖6 宏觀場增強因子變化規律Fig.6 Change law of macroscopic field enhancement factor

選取5種結構參數的環形陰極二極管進行模擬計算，將擬合結果和模擬結果進行比較(表1)。比較結果表明，當d/w<5時，擬合公式能較準確地計算出環形陰極的宏觀場增強因子，相對誤差小于10%。

表1 宏觀場增強因子的擬合結果和模擬結果比較Table 1 Comparison between fitting βE and simulation βE

4 結論

在均勻帶電細圓環空間電勢分布理論公式的基礎上，建立了環形陰極二極管中電場強度分布的理論計算模型，研究了環形陰極宏觀場增強因子隨二極管結構參數的變化規律。計算結果表明，在d/w<5的情況下，環形陰極宏觀場增強因子與d/w呈線性關系，并給出了宏觀場增強因子的經驗估算公式，與數值模擬結果的相對誤差小于10%。該計算方法已應用于軔致輻射反射三極管的束流損失特性研究中[17]，后續可為其他類型負載的環形陰極結構參數設計優化提供借鑒和參考。