高溫氣冷堆石墨構件的碰撞力學行為研究

祁志偉，王曉欣，史 力，王洪濤，孫立斌

(清華大學 核能與新能源技術研究院，先進核能技術協同創新中心，先進反應堆工程與安全教育部重點實驗室，北京 100084)

高溫氣冷堆(HTGR)和熔鹽堆(MSR)通常采用石墨和碳磚作為慢化劑和反射層，這些部件同時也是堆芯的支承結構，對核電站的安全至關重要。由于石墨是脆性材料，成品尺寸較小，反應堆中一般采用堆砌結構，磚與磚之間設有間隙，并通過石墨方鍵或圓榫來連接相鄰的磚塊。由于間隙的存在，石墨磚在動態激勵下會表現出非線性特征[1-4]。為研究這種大規模散體結構的動力特性，在過去的幾十年中針對棱柱式和球床式高溫氣冷堆兩種類型已開展了許多振動臺實驗和數值分析[1,4-10]。振動臺實驗由于實驗臺尺寸的限制，只能對部分構件或采用縮比模型進行測試，不能完全反映堆內石墨構件的動力特性。因此，數值分析是高溫氣冷堆堆內構件在地震載荷下安全性評價最為重要的方法。

山東石島灣200 MW球床模塊式高溫氣冷堆(HTR-PM)堆內構件包含的石墨磚或碳磚超過3 000個，方鍵或圓榫超過1萬個。采用細致的三維模型并考慮接觸和摩擦等碰撞特性的經典有限元方法對計算機要求非常高，且對結果的后處理非常困難，因此一系列簡化方法已被開發用于多種數值程序，如用于先進型氣冷堆的AGRCOR[11]，棱柱型HTGR的AGRCORUK7、CRUNCH-10、CRUNCH-20、MCOCO和GTOROTO等程序[1,12-14]。這些模型中磚塊被視為剛體質點，通過使用非線性連接器連接兩個剛體質點來模擬兩個構件間的相互作用，極大簡化了碰撞問題，提高了計算效率。數值模型的動態響應主要取決于連接器的剛度和阻尼，這些參數的合理性對于數值分析的準確性十分重要。

HTGR的石墨磚通過方鍵和圓榫進行連接，磚與磚之間主要有3種碰撞類型，為獲得這些典型碰撞形式下的連接單元屬性，本文對3種碰撞類型的實驗進行數值分析，通過實驗和數值分析得到的碰撞時間和恢復系數計算不同碰撞速度下Hertz模型的等效剛度系數和等效阻尼系數，并進一步研究碰撞間隙以及石墨磚質量對碰撞的影響。

1 碰撞實驗

為研究不同碰撞類型的動態行為，開展了3組實驗，分別為磚-磚、磚-圓榫與磚-方鍵碰撞實驗，其中第1組實驗(磚-磚碰撞)結果詳見文獻[15]。第2、3組實驗中，采用同樣尺寸的石墨磚放置于平行的軌道上，在待碰磚側面設置榫槽或鍵槽，主動碰撞磚塊沿相同的軌道以不同的速度撞向待碰磚塊，示意圖如圖1a、b所示。每組進行約130次碰撞實驗，碰撞速度在0.1～2.4 m/s之間。測量方式采用光學方法，在石墨磚表面制作一系列標記點，由高速攝像機拍攝極短時間內石墨翻轉的圖像，利用灰度重心法和二值法對標記點進行處理，得出各點的灰度重心坐標，進而獲得磚塊在碰撞過程中的位移情況，計算碰撞速度[15]。由于碰撞和待碰石墨磚均未固定在軌道上，因此無法測量碰撞過程中的相互作用力。

實驗件采用各項同性的石墨材料NG-CT-01(成都炭素有限責任公司)，其性質與HTGR中的IG110型號石墨類似，兩種材料的特性參數列于表1[16]。

a——第2組碰撞實驗；b——第3組碰撞實驗；c——第2組碰撞數值模型；d——第3組碰撞數值模型紅色：主動碰撞試件；綠色：待碰試件；藍色：鍵和榫圖1 碰撞實驗及數值模型示意圖Fig.1 Layout of collision test and numerical model

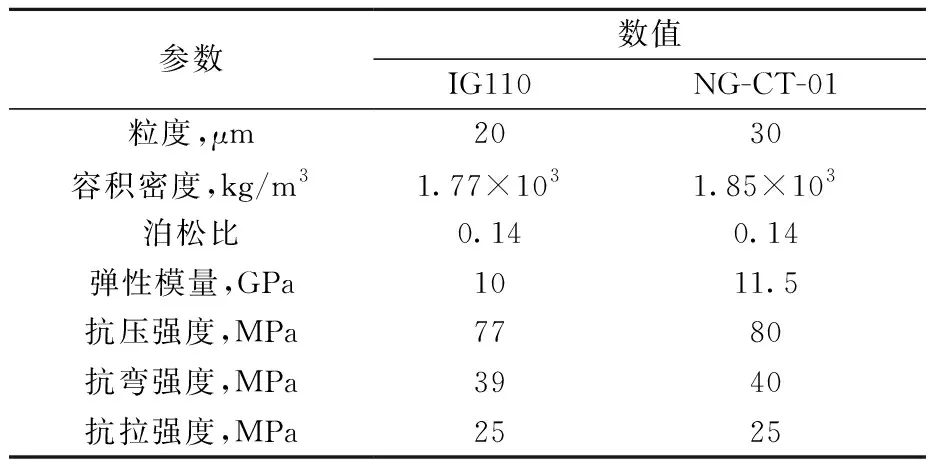
表1 石墨材料的主要特性參數Table 1 Main property parameter of graphite material

3組磚塊不同碰撞類型的典型速度曲線示于圖2。第1組速度曲線與經典碰撞模型的趨勢一致[16]，碰撞過程中兩塊磚之間的相對速度以相同的梯度急劇變化，可很容易地獲得碰撞時間和恢復系數。

第2、3組速度曲線與第1組差異較大，其碰撞時間約為100 ms，明顯大于第1組的2 ms，此外碰撞過程中速度曲線的斜率在圖2b中并不恒定。碰撞接觸開始時試件速度迅速改變，速度的斜率也在逐漸減小，直到石墨磚的速度保持恒定。實驗期間觀測到石墨磚的旋轉，原因可能是軌道的剛度不夠大，圓榫和石墨磚在碰撞過程中發生翻轉，導致了碰撞時間增加。盡管發生了翻轉，石墨磚速度的主要方向仍未發生變化，通過第2、3組碰撞實驗獲取的恢復系數可用于表示能量耗散機制，如圖3所示。第2、3組的恢復系數更為分散，變化趨勢也有所不同。恢復系數在碰撞速度為0～0.6 m/s時隨碰撞速度的增大而增大，在0.6～1.2 m/s時隨碰撞速度的增大而減小。

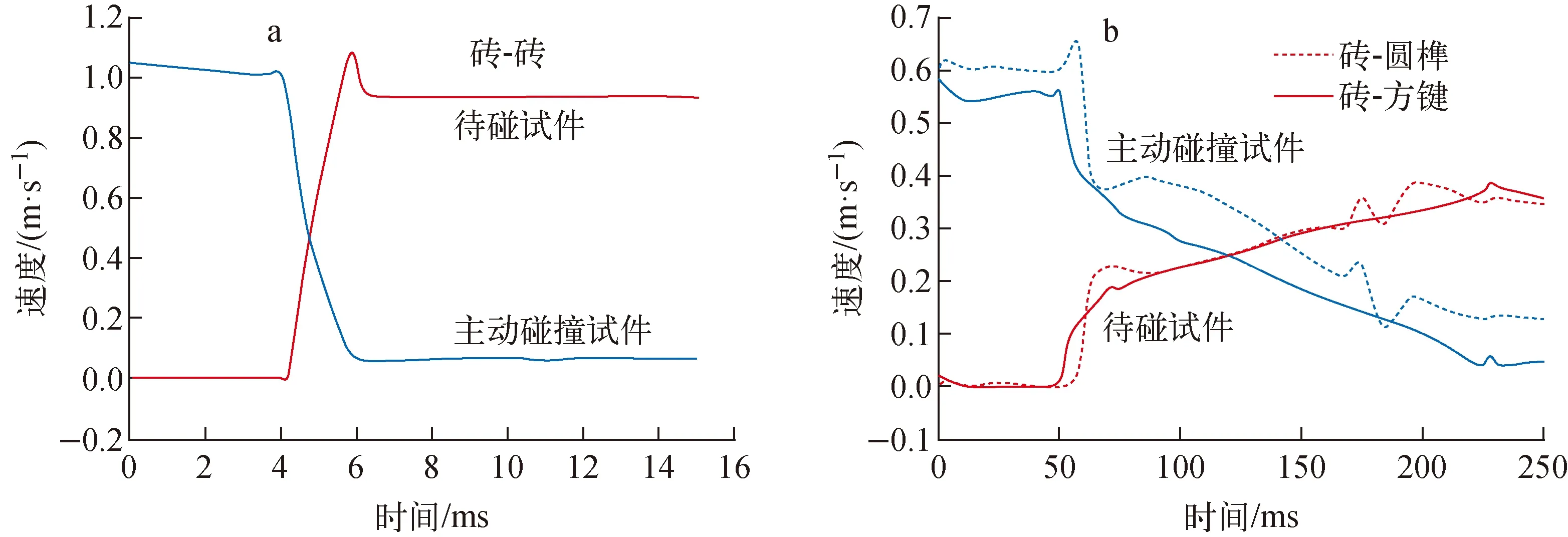
圖2 典型速度曲線Fig.2 Typical velocity curve

2 數值分析

第2、3組實驗的碰撞時間受到石墨磚翻轉的影響，但在實際反應堆中，石墨構件在豎直方向上有50層，上面還有其他限位構件，石墨磚圍繞水平軸的翻轉并不會發生，因此第2、3組實驗并不能代表反應堆中的實際情況。當采用合適的模型和材料參數時，有限元可合理分析石墨的碰撞行為，這在第1組實驗結果和有限元分析結果的對比中已得到了論證[15]。為進一步研究更復雜碰撞機制下的碰撞時間，本文使用商業有限元軟件ABAQUS來模擬上述兩組碰撞實驗。考慮到碰撞試件的幾何形狀和邊界條件的對稱性，為簡化計算過程，采用1/2模型進行模擬，以豎直方向的中面作為對稱面，與磚塊底面軌道相連節點受到x方向上的位移約束。在這種約束條件下，石墨本身不會發生翻轉，但在鍵榫與磚的間隙會導致鍵榫的輕微翻轉，與堆內實際情況相同。方鍵與磚之間的接觸設置為摩擦系數0.2的滑動摩擦[3]。通過網格敏感性分析后確定的有限元模型和網格劃分如圖1c、d所示。石墨材料特性參見文獻[16-17]。

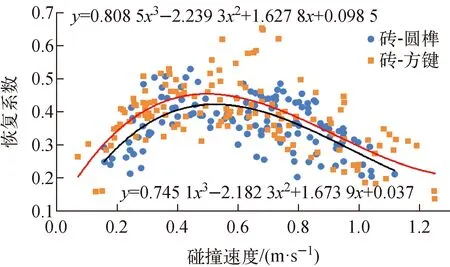
圖3 第2、3組實驗中恢復系數與碰撞速度的關系Fig.3 Restitution coefficient of collision test in group 2 and 3

分析中采用Rayleigh阻尼，其阻尼矩陣C定義如下：

C=αM+βK

(1)

其中：M為模型的質量矩陣；K為模型的剛度矩陣；α和β分別為每個矩陣的獨立因子。對于細級核石墨，文獻[17]建議使用以下α和β表達式：

α=15.0β=5×10-5(v0/v)2

(2)

其中：v0=1.0 m/s為碰撞參考速度；v為石墨磚碰撞相對初始速度。

初步分析發現，采用上述表達式時阻尼系數的數值分析結果與實驗結果有較大差距，這主要是由于磚與圓榫和方鍵碰撞的過程中接觸面積、應力水平與正碰實驗差別明顯。考慮到實驗中的恢復系數可代表實際碰撞，而β的影響更為顯著，因此對模擬過程中的β進行修改擬合，獲取與實驗結果相符的恢復系數，得出兩組實驗的阻尼系數β，如表2所列。

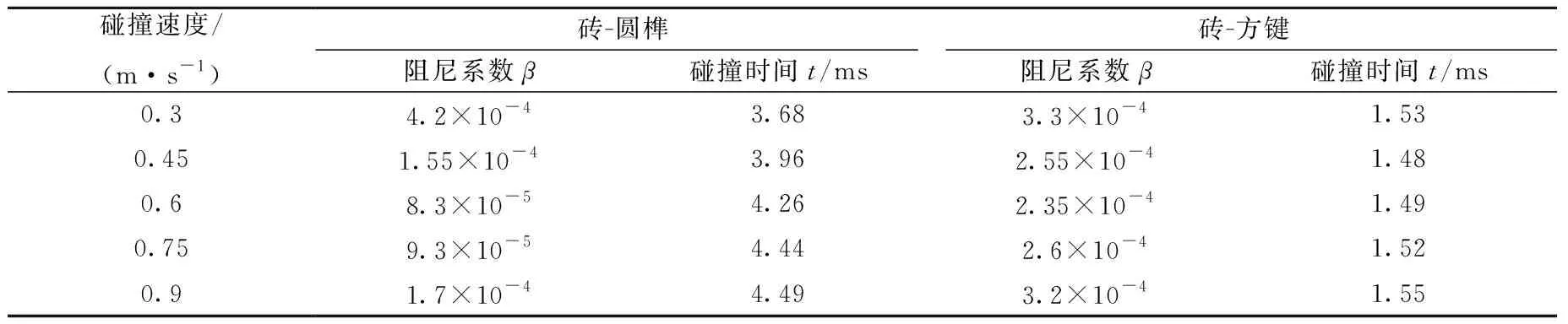
表2 數值分析得出的Rayleigh 阻尼系數β和碰撞時間tTable 2 Rayleigh damping coefficient β and collision time t in numerical analysis

使用有限元分析獲得的第2、3組實驗的典型速度曲線如圖4所示。與圖2b相比未觀察到磚的翻轉，此外，曲線的斜率在碰撞過程中呈梯度變化，這表明方鍵和圓榫的翻轉不明顯，因此模擬得出的碰撞時間可用于表示磚與方鍵或圓榫的實際碰撞時間，不同碰撞速度下的碰撞時間列于表2。

3 間隙及附加質量的影響

反應堆設計中，石墨磚的尺寸和部件之間的間隙是結構優化的主要內容，另外石墨在中子的輻照作用下可能發生體積收縮和膨脹[18]，為研究這些設計參數變化對石墨磚碰撞性能的影響，通過上述數值模擬得出磚-圓榫、磚-方鍵數值模型中修正的阻尼系數，進一步探索碰撞間隙及附加質量對碰撞過程的影響。

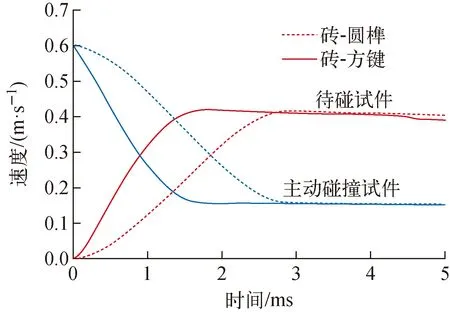
圖4 第2、3組實驗數值模型的典型速度曲線Fig.4 Typical velocity curve for test in group 2 and group 3

對于磚-圓榫碰撞，通過修改圓榫的截面半徑來改變碰撞間隙，分別設置了8組(0.3、0.4、0.6、1、1.5、2、3、4 mm)不同的間隙模型。對于磚-方鍵碰撞，通過修改方鍵在速度方向的長度來改變碰撞間隙，分別設置了7組(0.35、0.5、1、1.5、2、2.5、3 mm)不同的間隙模型。分別模擬碰撞速度在0.3、0.45、0.6、0.75、0.9 m/s下不同間隙的碰撞情況。磚-圓榫碰撞的恢復系數和碰撞時間與碰撞間隙的關系如圖5所示。隨著碰撞間隙的增加，石墨磚碰撞的恢復系數逐漸減小，碰撞時間不斷增加，這主要歸因于間隙增大使得圓榫的翻轉現象更加明顯。對于磚-方鍵碰撞，隨著間隙的增大，其恢復系數和碰撞時間并無明顯變化，主要原因是方鍵在碰撞過程中接觸面積較大且翻轉并不明顯，即使在一定范圍內增大碰撞間隙，也不會導致碰撞情況的改變。

通過在磚塊模型上附加無結構質量，進而改變碰撞模型的質量，以此研究相同榫鍵結構下，石墨磚質量對碰撞參數的影響。附加質量選取7組(0、0.1、0.3、0.6、1、1.5、2)不同因子(附加質量/自重)進行不同碰撞速度下的數值分析。磚-圓榫和磚-方鍵碰撞的恢復系數和碰撞時間與附加質量的關系如圖6所示。隨附加質量的增加，磚-圓榫碰撞的恢復系數減小，磚-方鍵碰撞的恢復系數增加，兩種類型的碰撞時間均隨附加質量而增大。

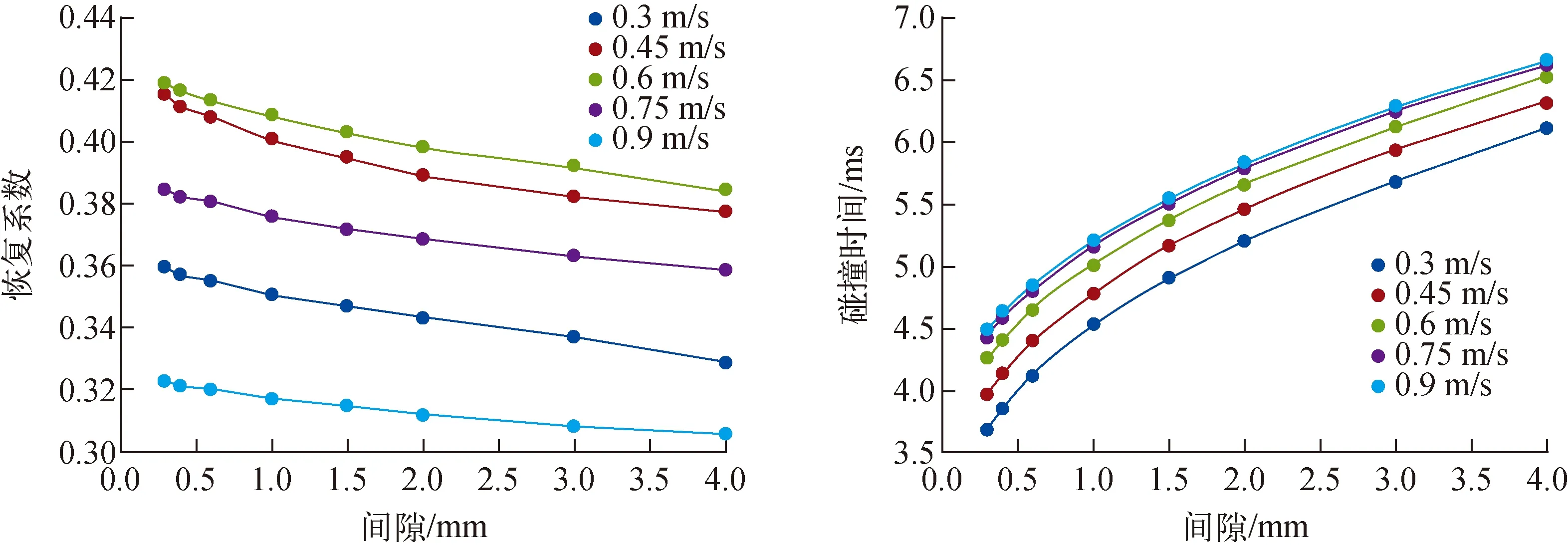
圖5 磚-圓榫碰撞恢復系數和碰撞時間與碰撞間隙的關系Fig.5 Restitution coefficient and collision time with different gaps in brick-dowel contact

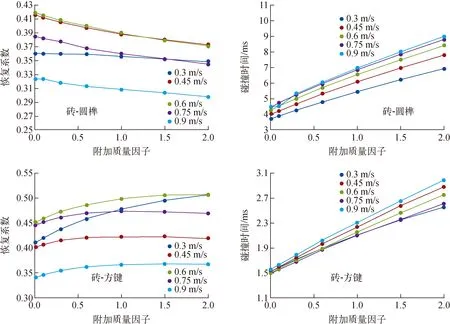
圖6 磚-圓榫和磚-方鍵碰撞恢復系數和碰撞時間與附加質量的關系Fig.6 Restitution coefficient and collision time with additional mass in brick-dowel and brick-key contacts

4 Hertz模型的參數計算

根據經典的碰撞理論，接觸力F和碰撞間隙之間的關系可描述為：

(3)

其中：K為等效剛度系數；C為等效阻尼系數；δ為碰撞過程中的相對位移；δ′為碰撞物體的相對速度。當n=1且m=0時，式(3)表示Kelvin-Voight模型[12]；當n=m>1時，表示Hertz模型。目前大部分反應堆石墨構件數值模型中均采用將K和δ之間假定為線性關系的Kelvin-Voight模型，該模型的K和C可通過碰撞過程中的碰撞時間和恢復系數(碰撞后和碰撞前相速度的比值)推導得到[12]，其中碰撞時間主要影響等效剛度系數K，恢復系數e則與等效阻尼系數C相關。

Kelvin-Voight模型形式簡單，可較易應用到有限元分析軟件中，但有一定的局限性。該模型在碰撞過程中等效阻尼系數是恒定的，且由于在碰撞開始階段引入阻尼力，這種情況與實際不符合。相比之下，Hertz模型能更準確地表示碰撞行為，已應用于建筑物的碰撞分析[19]，然而尚未在反應堆石墨構件的動力學分析中得到應用。

方程(3)適用于球狀物體的碰撞，對于磚塊與圓榫的碰撞，由于接觸面積較小，根據類似結構的靜力實驗結果，取n=m=2[3]。等效剛度系數K主要由碰撞時間確定，它隨碰撞時間的增大而減小。將兩個碰撞物體視為質點，可通過數值方式通過MATLAB軟件對運動過程(式(3))進行求解，獲得K與碰撞時間的關系，當計算的碰撞時間與第1組實驗和有限元分析(第2、3組實驗)中的結果相同時，該剛度即為合理的碰撞單元等效剛度。等效阻尼系數C表達式[20]如下：

(4)

其中，δ′0為碰撞的相對初始速度。根據式(1)、(4)，當K已知時，可通過實驗測量得到的恢復系數來計算等效阻尼系數。

采用上述方法計算的等效剛度系數與等效阻尼系數如圖7所示。

為研究間隙和附加質量對碰撞參數的影響，采用同樣方法計算其等效剛度系數和等效阻尼系數，結果如圖8所示。由于間隙的增大對磚-方鍵碰撞影響很小，因此其等效剛度系數和等效阻尼系數的曲線與圖7相同。從圖8可看出，隨著速度的增加，等效剛度系數和等效阻尼系數逐漸減小。

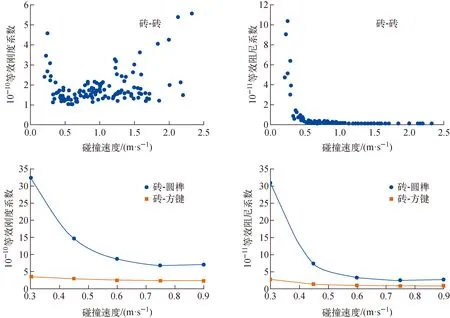
圖7 第2、3組碰撞實驗的等效剛度系數和等效阻尼系數Fig.7 Equivalent stiffness and damping coefficients for group 2 and group 3

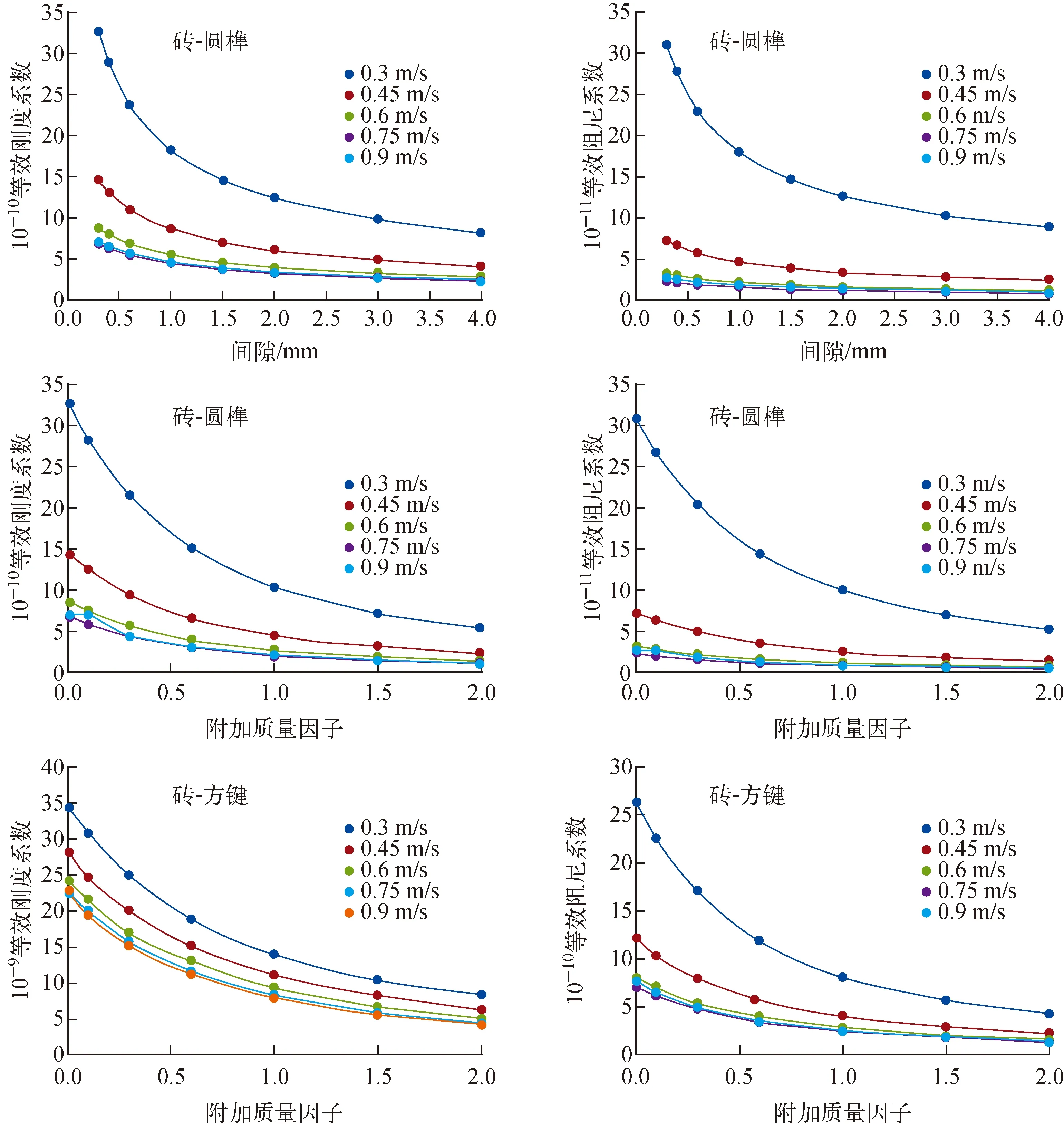
圖8 不同影響因素下磚-圓榫和磚-方鍵碰撞實驗的等效剛度系數和等效阻尼系數Fig.8 Equivalent stiffness and damping coefficients for brick-dowel and brick-key contact under different influence factors

圖5、6中磚-圓榫和磚-方鍵的恢復系數和碰撞時間隨碰撞速度的增加無明顯的變化規律，然而圖7、8中簡化Hertz模型的等效剛度系數和等效阻尼系數均在碰撞速度較大時趨向較為穩定的值。這是由于碰撞速度較小情況下，碰撞時榫鍵在鍵槽內的翻轉滑動對恢復系數和碰撞時間有明顯的影響；榫鍵翻轉后與石墨磚完全接觸到位，各部件的形狀位置不再發生非線性變化，結構的響應主要為線彈性變化，因此碰撞速度較大時等效剛度系數與等效阻尼系數變化不大。當間隙與石墨磚質量增加時，Hertz碰撞單元的等效剛度系數和等效阻尼系數均有所降低，碰撞速度引起的差異也逐漸減小，這些結果可直接用于高溫氣冷堆石墨堆內構件的動力學分析模型中，以指導石墨散體結構的設計優化。

5 結論

本文通過細顆粒核級石墨磚的碰撞實驗和數值分析，獲得了磚-磚、磚-圓榫和磚-方鍵3種不同碰撞類型的碰撞時間和恢復系數，以及磚-圓榫和磚-方鍵結構的材料阻尼系數。基于實驗和數值分析結果，采用改進的Hertz模型計算了簡化碰撞單元的等效剛度系數和等效阻尼系數。通過驗證的數值模型，進一步探究了磚和連接鍵榫間的間隙以及磚塊質量對石墨磚碰撞行為的影響，獲得了不同設計條件下碰撞單元的參數。這些參數將為HTGR中石墨內部構件的地震分析和評估提供重要依據，并為其他堆型石墨堆內構件的設計與優化提供參考。