基于邏輯回歸模型的瓦斯濃度異常值檢測與預警*

廖英雷

(西安科技大學 計算機科學與技術學院，陜西 西安 710054)

0 引言

2019年上半年全國煤礦企業共發生事故67起，其中因瓦斯事故死亡人數占比42%，可見瓦斯事故是煤炭安全生產的最大威脅[1]。通過對瓦斯數據的監測和異常數據的檢測來預警危險，對煤礦的安全生產有重大意義。煤炭的采出必然破壞巖層的原始平衡狀態而引起巖層運動，從而導致瓦斯涌出或突出，為生產帶來風險[2]。在煤層產狀不穩定的條件下，瓦斯突出點主要分布在煤層應力較集中且應力梯度變化較大部位[3]。工作面采掘機的工作會改變煤層的應力，從而導致瓦斯突出，在通風不變的情況下，隨著時間增加瓦斯濃度也隨之增加，會帶來瓦斯濃度超限的風險。目前瓦斯傳感器主要采用頻率信號傳輸，僅能輸出單一數據信息，無法掌握更多的運行信息。當傳感器監測值異常時，只能依靠人工推斷傳感器運行狀態[4]。

隨著國內外學者專家對煤礦開采的瓦斯濃度數據分析，對數據的不確定性進行深入研究，發現井下瓦斯數據的變化深刻影響煤礦生產安全。周鑫[5]研究了基于分類的時間序列異常檢測方法及特征屬性降維方法，并應用于礦井瓦斯異常檢測；彭泓[6]等采用再生核算法來進行RBF神經網絡的訓練，通過W12[a，b]空間插值逼近的方法，把RBF神經網絡的訓練轉換為解線性方程組，從而準確地預測出了瓦斯突出；吳海波[7]等采用流回歸機器學習算法與正態統計分布技術相結合的方法來建立瓦斯濃度流數據異常檢測模型，實時判斷流數據中的異常，提高了瓦斯風險評價時效；敖培[8]等基于改進的加權歐氏距離對瓦斯濃度異常數據進行處理，分析出設備異常數據、噪聲數據和瓦斯突出孤立點數據。韓磊[9]通過建立瓦斯涌出量混沌預測數學模型，根據瓦斯濃度預測結果及其預測區間進行預警閾值計算，并對其對應的預警等級進行劃分，完成預警信息。基于分類的瓦斯濃度異常值檢測隨著監測時間的增加數據的累計，會造成該算法的不穩定，不能更準確的分別異常數據。而神經網絡的算法有較好的識別準確率，但算法復雜，數據量較大時需要對數據進行長時間的分析；利用損失函數易于計算的線性算法做成流式回歸機器學習算法有一定的局限性；基于改進的加權歐氏距離的算法隨著新數據的增長需要重新計算歐氏距離；建立瓦斯涌出量混沌預測數學模型的方法由于參與計算的數據比較多，實時性較差。為此，使用邏輯回歸模型對時間序列瓦斯濃度數據進行檢測與分析，判斷出風險所在，降低對人工分析的依賴，為排除風險提供可靠的依據。判斷異常數據，能在時間復雜度相對低的情況下較為準確的分析出異常數據，且有一定的實時性。

1 瓦斯相關數據預處理

1.1 試驗數據采集

采集范圍：試驗數據來自陜北某礦的瓦斯濃度數據，經勘探該礦區煤層處于瓦斯風化帶中，瓦斯含量在0．05～6.49 mL/g·r；煤層原始瓦斯壓力為1.2～1.59 MPa；煤層瓦斯相對含量為9.32～11.73 m3/t；透氣性系數11.49 m2/MPa2·d；該區煤層含氣量高，煤層透氣性好，瓦斯壓力大[10]。采煤區在進行勘探后，會進行6～12個月的預抽采以降低煤層的瓦斯含量，當抽采達標后進行生產。該數據是實時監測的采煤工作面上隅角瓦斯濃度數據，數據間隔取1 min，瓦斯濃度數據范圍是0%～100%，并且在0%～5%濃度范圍內其測量誤差小于±0.06%。采煤工作面上隅角瓦斯濃度傳感器T0分布，如圖1所示。

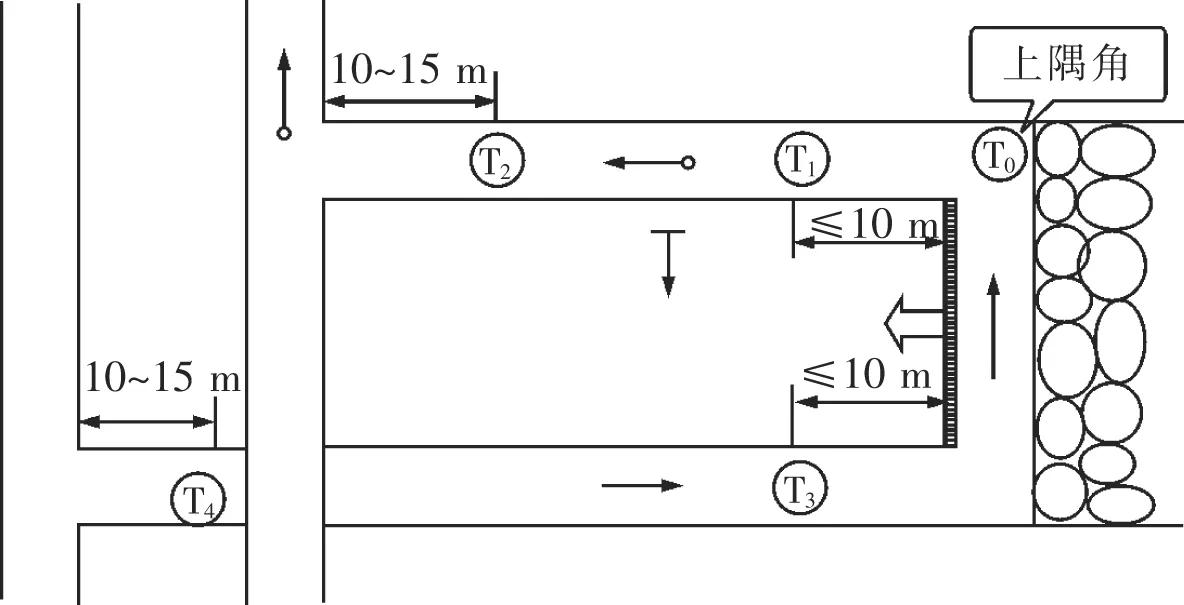
圖1 傳感器位置分布

采集方法：風由進風巷吹到工作面，帶走工作面的瓦斯，上隅角的傳感器對氣體進行檢測，帶瓦斯空氣隨著回風巷排到通風巷道，因此上隅角的瓦斯濃度數據能反映工作面瓦斯濃度的變化。根據國家和礦區規章制度，礦區瓦斯濃度傳感器裝備數量和報警濃度的規則制度見表1[11]。如圖2所示，數據組1來自該礦區的803工作面7 d的瓦斯濃度數據，用作訓練數據，采集間隔為1 min，其中有異常數值31個，監測數據最大濃度2.11%，最小值為0.01%，平均值為0.253%，標準差為0.104%，大部分數據在瓦斯濃度0%～1%之間進行有規律的波動。另有數據組2來自工作面采集8 h的數據作為測試數據如圖3所示，采集間隔為1 min，最大濃度為0.58%，最小濃度為0.08%，均值為0.212%，標準偏差為0.117%，數據集隨時間進行規律波動。

圖3 8 h工作面瓦斯濃度隨時間變化散點圖

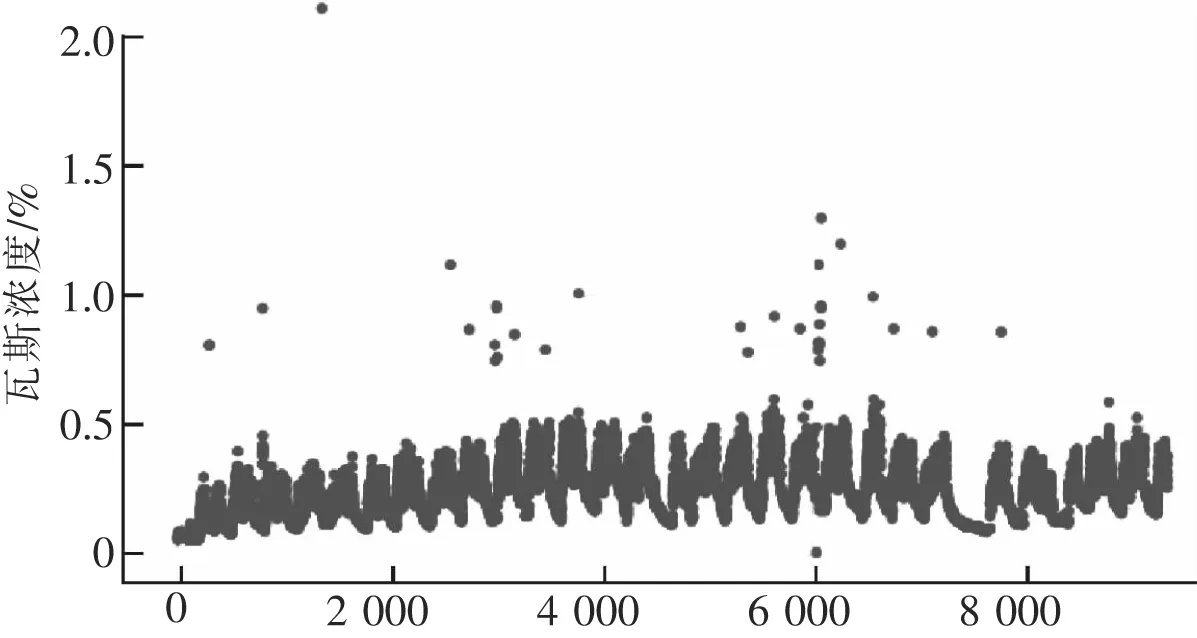
圖2 1周工作面瓦斯濃度變化散點圖

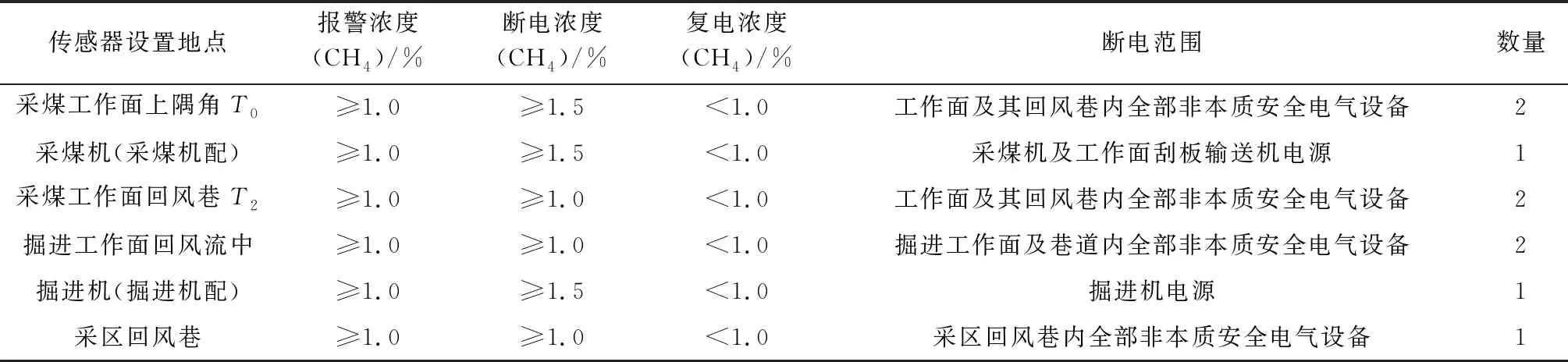
表1 瓦斯濃度傳感器裝備數量

數據處理的必要性：井下瓦斯濃度的情況僅依據國家和礦區的規章制度來判斷是否報警還是斷電是有弊端的，當采掘工作面沒有開始工作處于檢修狀態時，采集到的瓦斯數據大部分在0.0%～0.2%之間，此時檢測到異常數據若為0.6%未超過1.0%的報警上限，監測監控系統選擇不報警是有可能帶來風險的。因此，要對采集到的瓦斯濃度數據進行即時有效的分析，規避井下瓦斯突出等風險因素。

1.2 數據的分析與預處理

缺失數據插補：煤礦的原始數據一般包含異常數據(噪聲)，因此在用機器學習的辦法進行數據分析和建模前，就要對異常數據進行預處理來適應模型。異常數據包括：缺失值、異常值、不一致的值、重復數據及含有特殊符號(如#、￥、*等)的數據。本次研究瓦斯濃度的異常數據，只需將瓦斯監測設備的故障、通信信號被干擾等原因采集到的缺失值(如null)，濃度數據為100%或者0%及含有特殊符號(如#、￥、*等)的數據進行處理，對這些數據采用插補的辦法進行處理，常用的方法見表2。

表2 常用的缺失數據插補方法

回歸模型分析：以間隔1 min采集到一周瓦斯濃度數據有9 360個，缺失值為14個，缺失值較少且瓦斯數據會隨時間變化添加新數據。當設備故障時缺失數據是連續的，對該數據用回歸方法插補進行補差，回歸方法插補根據已有數據和與其有關的其他變量數據建立擬合模型來預測是無偏估計，雖容易忽視隨機誤差，但較為適合具有線性關系的數據。瓦斯數據的P-P圖如圖4所示，點的分布接近直線y=x線進行分布且比較對稱；在如圖5所示，點分布于y=0兩側且對稱，可看出瓦斯濃度數據分布也符合Logistics回歸模型。

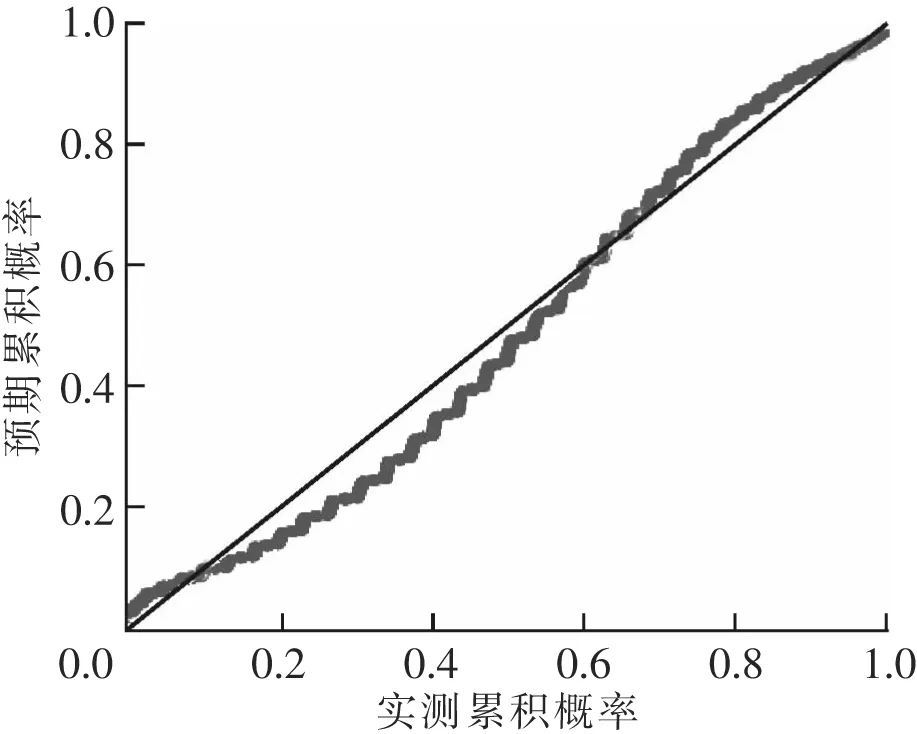
圖4 瓦斯濃度Logistics P-P圖

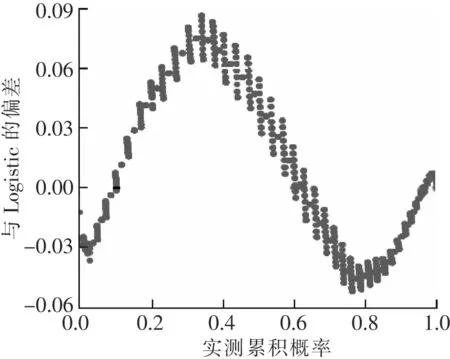
圖5 瓦斯濃度Logistics去趨勢P-P圖

2 邏輯回歸分析

2.1 邏輯回歸分析的作用

邏輯回歸介紹：邏輯回歸(Logistic Regression)是一種用于解決二分類(0/1分類)問題的機器學習方法，用于估計某種事物的可能性。邏輯回歸(Logistic Regression)是廣義線性模型(generalized linear model)其中一種。該模型通過假設因變量y服從伯努利分布，自變量x與因變量y存在線性關系，利用Sigmoid函數處理非線性數據，從而解決二分類問題。

邏輯回歸分析的作用：當工作面的瓦斯濃度數據異常時但未達到報警濃度為1%的閾值，通過邏輯回歸模型對數據進行分析，不僅能檢測出異常數據還可提前數分鐘進行預警從而幫助礦區提前排除風險或者調整工作面刀頭速度保證安全生產。

2.2 邏輯回歸模型的建立

建立過程：邏輯回歸模型的建立需要以下過程，首先要建立代價函數，然后通過優化方法迭代求解出最優模型參數，最后測試驗證得到邏輯回歸模型。

建立代價函數：瓦斯濃度數據集t包含t1，t2，…,tn，這些數據賦予一個權值w，帶有權值的瓦斯濃度數據wTt計算見式(1)

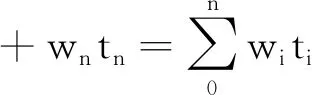
(1)

定義f(t)=wT·t，定義函數g(i)=Sigmiod(i)見式(2)，Sigmiod函數其函數圖像如圖6所示，值域是[0，1]。

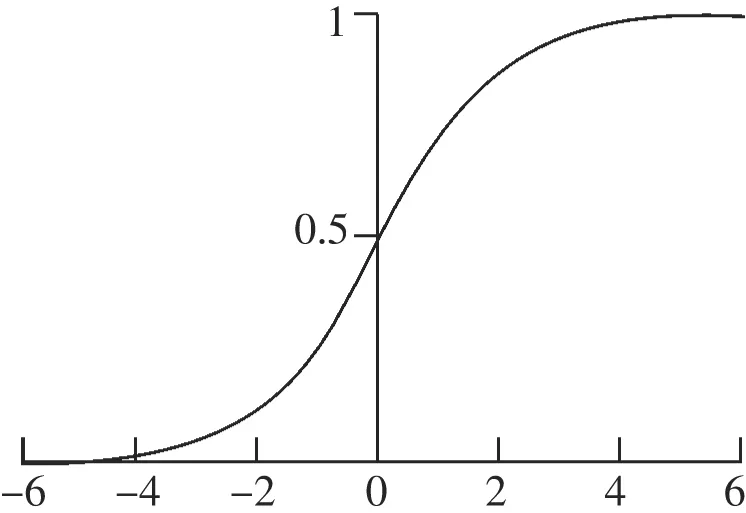
圖6 Sigmiod函數圖像

(2)

樣本數據正反類劃分：用函數g(i)映射f(t)，當f(t)≥ 0.5時，表示t被分到正類，當f(t)<0.5時，表示t分到反類，f(t)的數值在[0，1]之間可看為概率。此時瓦斯濃度數據已經能被劃分出2類，分類函數記為P(y|t)，也可記為P(y|x)。定義h(x)表示預測出的樣本數據是正類的概率，則反類的概率為1-h(x)，定義讓步比為正類和反類的比值，取對數計算見式(3)，并用對數求解得式(4)

(3)

(4)

模型的預測函數：將帶有權值的瓦斯濃度數據代入函數f(x)進行非線性求和得h(x)，如圖7所示，用g(i)函數映射f(x)得到h(x)，即h(x)→g(f(x))，代入瓦斯濃度數據，對進行加權求和與非線性輸出得出h(x)，如圖8所示。函數h(x)有Sigmiod函數的特性為模型的預測函數。

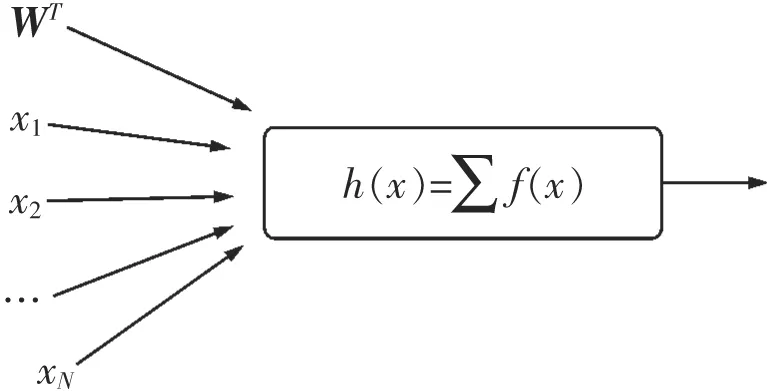
圖7 線性模型加權和

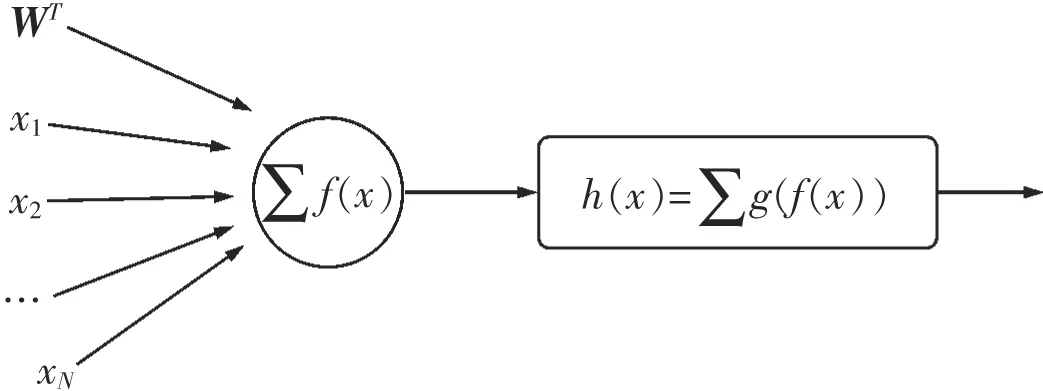
圖8 加權和非線性輸出

瓦斯濃度數據計算：瓦斯濃度數據是已經知結果，需要尋找使得該結果出現的概率最大的條件，構造函數選擇似然函數，似然函數是統計模型函數中參數的函數。利用瓦斯濃度數據進行參數估列。建立似然函數L(w)，每個樣本互相獨立，n個瓦斯濃度數據樣本出現的似然度為式(5)

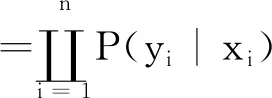
(5)

取函數L(w)的自然對數得l(w)，化簡計算見式(6)，為損失函數Loss函數與f(x)的關系。

(6)

對損失函數進行最優化，得到對應的f(x)，以此找回歸因子W，對參數W求偏導數并化簡得式(7)

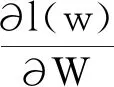
(7)

以上步驟得到f(x)，知l(w)為損失函數，l(w)求偏導數，得梯度上升公式(8)。a表示每次迭代上升的幅度，利用瓦斯濃度數據與時間的數據來尋找回歸因子W逼近最合理的參數列表。

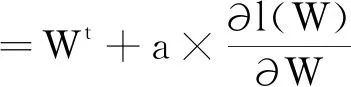
(8)

若將w=w+a×x.T×(y-h(x))定義為梯度上升公式，其隨機梯度上升為w=w+a×x[j，：].T×(y[j，：]-h(x))，是從所有的數據樣本矩陣x和y樣本中隨機選出的一個數據點來計算梯度并更新參數，有新的樣本數據增加時只需要對模型進行增量式更新。

2.3 瓦斯濃度數據訓練及分析

瓦斯濃度數據訓練：瓦斯濃度數據的訓練數據集D的屬性有3個：C，T，V。瓦斯濃度數據集合為C中有數據C1、C2…，Cn；時間T以分鐘為單位；該時刻瓦斯濃度數據是否為異常值V(是異常數據為1不是為0)。通過已經監測出來的瓦斯濃度數據利用公式求出預測函數h(x)，求得擬合預測數據h(T)。訓練數據中有異常數據n個，計算擬合預測值與實測值的相對差值di=|Ci-h(T)|，閾值Threshold按照Sigma原則取值。對比di與閾值的大小，當di大于閾值時則記該時刻瓦斯濃度數據為異常數據，檢測出來的異常數據個數與n進行對比選擇合適的Sigma。

瓦斯濃度數據分析：測試集需要分析的瓦斯濃度數據集的屬性有S(測試集瓦斯濃度實測值)和T(時間)。利用訓練出來的回歸模型用于測試數據集，得到擬合回歸數據h(T)，計算擬合預測值與實測值的相對差值dj=|Sj-h(T)，將數據的相對差值dj與模型閾值Threshold進行對比，當dj≤Threshold時，該M時刻的瓦斯數據為正常數據，當dj>Threshold時，此刻的瓦斯濃度數據為異常數據，需要進行預警。

3 試驗與分析

3.1 閾值選取

數據統計：該數據來自陜北某礦的803綜采工作面的回風隅瓦斯傳感器采集間隔為1 min的7 d的瓦斯濃度數據作為訓練數據。通過分析統計，該監測點最大濃度2.11%，最小值為0，平均值為0.253%，標準差為0.104%。對該瓦斯濃度數據的P-P圖如圖9所示，可以看出圖中點的分布幾乎符合y=x，則說明該數據符合正態分布。繪制瓦斯濃度數據的正態分布圖如圖10所示。

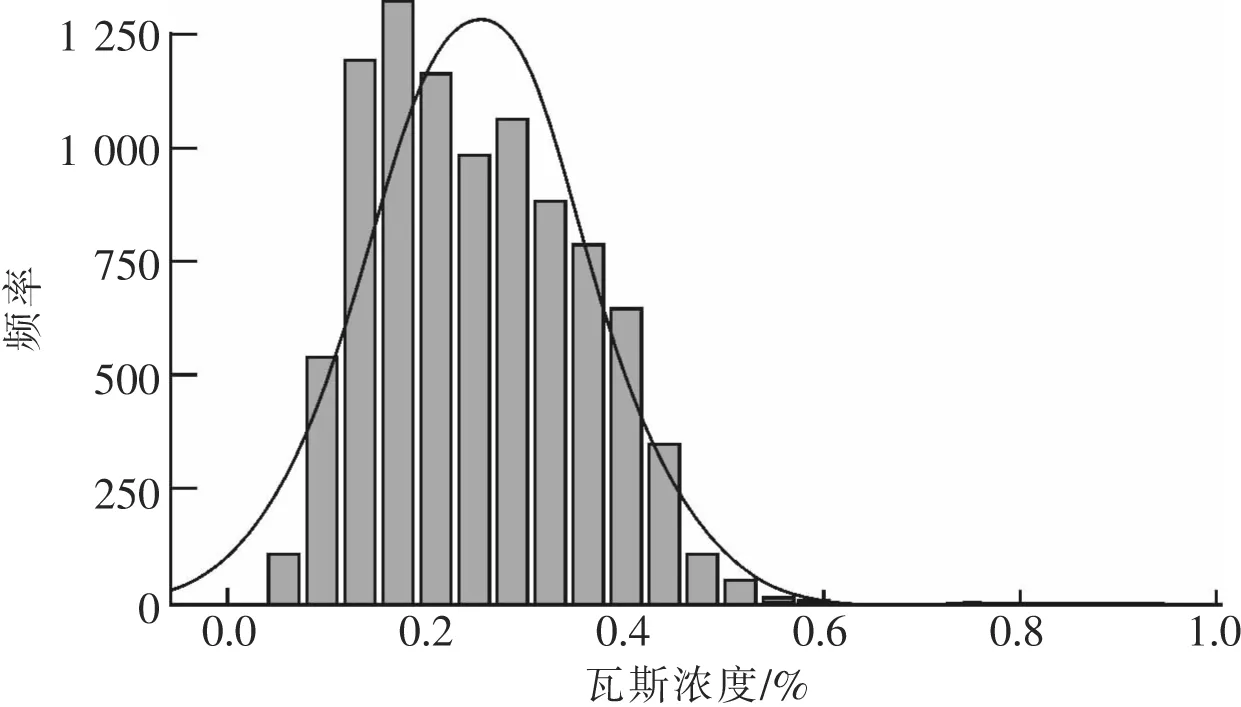
圖10 瓦斯濃度正態分布

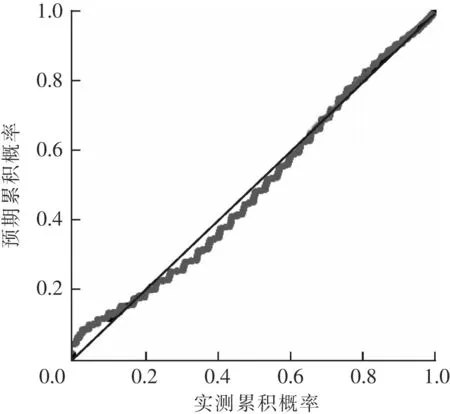
圖9 瓦斯濃度數據正態P-P圖

閾值確定：閾值需要根據Sigma原則進行取值，從正態分布圖來看，(μ-σ，μ+σ)中的概率為0.652 6，其中μ近似于0.3，σ近似于0.1。閾值Threshold=μ+kσ(k=1，2，3)。對訓練數據集用邏輯回歸模型進行分析，得到結果如圖11所示。其預測方程式為1/(0.166 666 666 666 666 7+4.967 385 168 684 82×0.999 959 195 617 732 7×x)，閾值Threshold=μ+kσ(k=1，2，3；μ=0.3%；σ=0.1%)。當k=1時，檢測出異常數據31個；當k=2時，檢測出異常數據28個；當k=3時，檢測出17個異常數據。由于訓練集的異常數據n=31，所以k=1時，閾值設為0.4%比較適合。

圖11 訓練數據進行邏輯回歸預測

3.2 模型應用

測試結果：數據組2是在工作面連續采集8 h的瓦斯濃度數據，時間間隔為1 min，作為測試集數據，其中包含15個異常瓦斯濃度數據。該組數據統計范圍有0.84%，最大值0.92%，最小值0.08%。用經過訓練的Logistics回歸模型對其進行分析，如圖12所示，閾值取0.4%，預測出相應的瓦斯濃度數值并根據其與實測數據的相對距離來判斷是否為異常數據。此組數據共檢測出13個異常數據，準確率為0.867%。

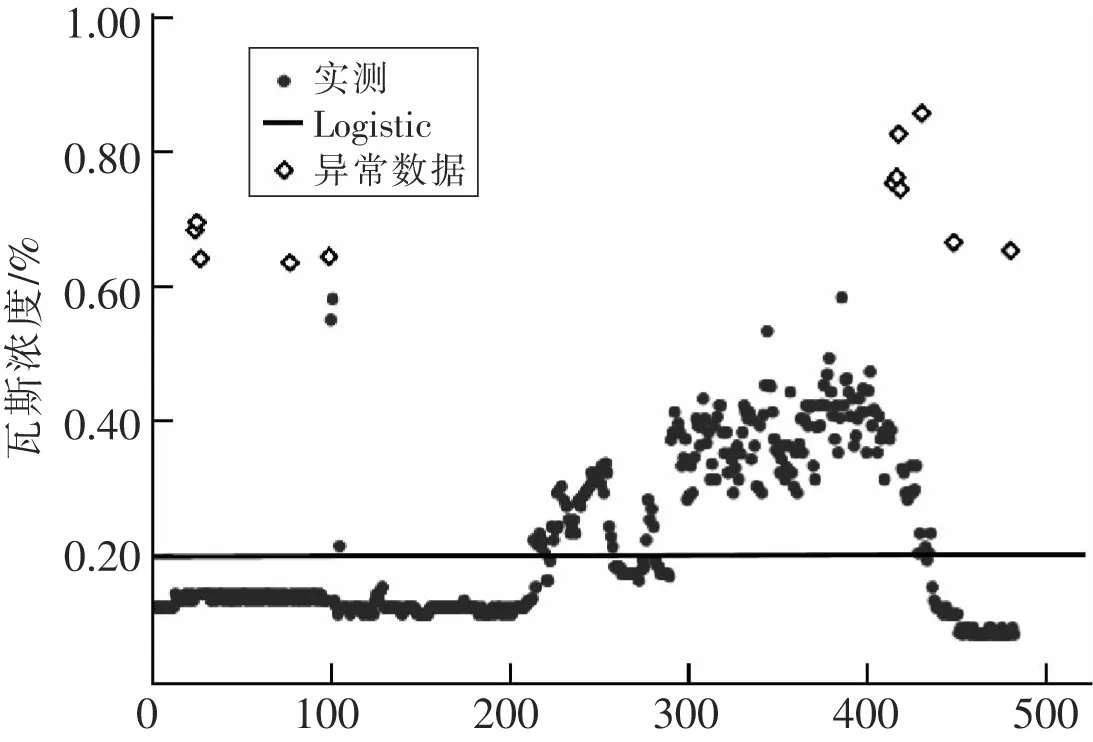
圖12 邏輯回歸模型分析測試數據

異常數據分析：測試集數據情況特殊，在工作面進行檢修時，上隅角傳感器采集到數據中有異常數據，需要預警。但采煤機沒有工作，煤層的應力結構沒有遭到人為破壞[12]，因此瓦斯濃度異常數據的產生是由于地殼結構的變化導致瓦斯突出[13]。

4 結論

(1)邏輯回歸模型中的隨機梯度上升算法是一個在線學習的算法，能減少計算機資源的利用，保證系統的穩定。通過邏輯回歸模型對瓦斯濃度的異常值進行檢測，判斷此時是否有異常情況發生，識別異常數據的正確率達85%以上，能夠實現提前預警。

(2)利用一部分數據對邏輯回歸模型進行分析，得到相關參數，樣本數據隨著時間的累加，通過不斷檢測異常數據的過程，該模型能得到越來越多較好的參數，使得模型對異常數據的檢測會越來越準確。

(3)通過試驗結論與數據分析，可以利用邏輯回歸模型基于不同閾值的情況下，建立一個分級報警的瓦斯濃度異常值檢測系統，有效識別未達到閾值上限的瓦斯數據是否存在異常狀態，這對優化礦井瓦斯濃度的檢測與預警提供了新方法。

本文寫作過程中得到了王安虎博士、曹健博士的支持和幫助，在此深表感謝！