基于神經(jīng)網(wǎng)絡(luò)和證據(jù)理論的火箭發(fā)動(dòng)機(jī)故障診斷

孫成志，閆曉東,2

(1. 西北工業(yè)大學(xué)航天學(xué)院, 西安 710072； 2. 陜西省空天飛行器設(shè)計(jì)技術(shù)重點(diǎn)實(shí)驗(yàn)室, 西安 710072)

0 引言

隨著航天科技的發(fā)展，高可靠性逐漸成為航天發(fā)射任務(wù)的追求目標(biāo)。在全箭眾多的故障模式中，動(dòng)力系統(tǒng)故障是運(yùn)載火箭最常發(fā)生、造成后果最嚴(yán)重的故障，輕則使運(yùn)載火箭入軌精度降低，重則直接導(dǎo)致飛行任務(wù)失敗[1-2]。因此，研究運(yùn)載火箭發(fā)動(dòng)機(jī)故障診斷具有非常重要的工程價(jià)值和實(shí)際意義。

運(yùn)載火箭動(dòng)力系統(tǒng)模式復(fù)雜，建立系統(tǒng)的解析模型十分困難，故障診斷正確率不高[3]。目前，針對(duì)運(yùn)載火箭動(dòng)力系統(tǒng)故障診斷方法層出不窮，基于信號(hào)檢測(cè)的故障診斷方法[4]、模糊理論的故障診斷方法、專家系統(tǒng)的故障診斷方法以及一些常規(guī)的故障診斷方法存在很大的局限性和適用性較差的問(wèn)題[5]。然而，基于神經(jīng)網(wǎng)絡(luò)的故障診斷方法，處理數(shù)據(jù)能力較強(qiáng)，適合處理數(shù)據(jù)量豐富的運(yùn)載火箭發(fā)動(dòng)機(jī)數(shù)據(jù)[6]，同時(shí)，神經(jīng)網(wǎng)絡(luò)良好的非線性特性也適合對(duì)故障模式繁多、故障原因復(fù)雜的非線性運(yùn)載火箭動(dòng)力系統(tǒng)進(jìn)行故障診斷[7]。但是神經(jīng)網(wǎng)絡(luò)容易陷入局部極小值，有時(shí)只能得到局部最優(yōu)解，可能會(huì)出現(xiàn)誤診的情況。在進(jìn)行故障診斷時(shí)，不同故障特征相互混雜在一起會(huì)出現(xiàn)多耦合、模糊性等復(fù)雜特征[8]，因此不能利用單一的方法判斷故障模式。證據(jù)理論在無(wú)需先驗(yàn)知識(shí)的情況下，能夠根據(jù)自身的算法融合不同方法的結(jié)果并以推理的形式獲得確定的結(jié)果[9]，已經(jīng)成為故障診斷領(lǐng)域的熱點(diǎn)方向。

禹建麗等[10]通過(guò)構(gòu)建BP神經(jīng)網(wǎng)絡(luò)、RBF神經(jīng)網(wǎng)絡(luò)和GRNN(廣義回歸神經(jīng)網(wǎng)絡(luò))故障診斷模型對(duì)變壓器進(jìn)行故障診斷。張煒等[11]通過(guò)建立復(fù)雜設(shè)備故障診斷的多重神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)，將其應(yīng)用于液體火箭發(fā)動(dòng)機(jī)渦輪泵的故障診斷。劉兵等[12]提出了一種基于模糊神經(jīng)網(wǎng)絡(luò)的故障診斷方法，較好地解決了固體火箭發(fā)動(dòng)機(jī)地面試驗(yàn)系統(tǒng)的不確定故障診斷問(wèn)題。郝大鵬等[13]運(yùn)用PNN(概率神經(jīng)網(wǎng)絡(luò))建立故障診斷模型，對(duì)汽車尾氣進(jìn)行分析并診斷發(fā)動(dòng)機(jī)故障。盧俊文等[14]通過(guò)改進(jìn)L-M算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)算法，對(duì)航空發(fā)動(dòng)機(jī)氣路故障進(jìn)行診斷。汪廣洪等[9]運(yùn)用BP網(wǎng)絡(luò)良好的非線性映射能力和D-S證據(jù)理論基本概率分配計(jì)算的客觀化能力，提出基于BP神經(jīng)網(wǎng)絡(luò)和D-S證據(jù)理論信息融合的航天器故障診斷方法，但并未給出仿真算例驗(yàn)證。張雷[15]提出一種基于重組粒子群算法的神經(jīng)網(wǎng)絡(luò)故障診斷方法，對(duì)滾動(dòng)軸承故障進(jìn)行診斷。劉小明[16]針對(duì)運(yùn)載火箭的復(fù)雜特性以及傳統(tǒng)BP算法的收斂速度慢、極易陷入局部極小的缺點(diǎn)和實(shí)際的故障樣本少的特性，提出了一種基于故障樹(shù)和SVM算法神經(jīng)網(wǎng)絡(luò)的故障智能診斷方法。李化南[6]在BP網(wǎng)絡(luò)結(jié)構(gòu)的基礎(chǔ)上，提出了一種基于BP網(wǎng)絡(luò)的3層診斷模型，對(duì)液體火箭發(fā)動(dòng)機(jī)的故障模式進(jìn)行診斷。

雖然國(guó)內(nèi)外許多學(xué)者在故障診斷方面做了很多研究，但是在神經(jīng)網(wǎng)絡(luò)的應(yīng)用層面上，大多數(shù)都是使用單個(gè)網(wǎng)絡(luò)進(jìn)行診斷，之后將各個(gè)網(wǎng)絡(luò)的診斷結(jié)果進(jìn)行對(duì)比，這樣很容易出現(xiàn)誤診的情況；也有學(xué)者將多個(gè)網(wǎng)絡(luò)融合，但是診斷網(wǎng)絡(luò)較為簡(jiǎn)單，只適用于已經(jīng)存在的故障模式，對(duì)于未參與網(wǎng)絡(luò)學(xué)習(xí)的故障模式無(wú)法診斷，并且無(wú)法估計(jì)故障模式下具體的特征參數(shù)。因此本文提出了基于神經(jīng)網(wǎng)絡(luò)和證據(jù)理論的方法對(duì)運(yùn)載火箭發(fā)動(dòng)機(jī)故障模式進(jìn)行診斷，并通過(guò)滾動(dòng)時(shí)域估計(jì)方法對(duì)運(yùn)載火箭飛行狀態(tài)特征量進(jìn)行估計(jì)，對(duì)于未參與網(wǎng)絡(luò)學(xué)習(xí)的故障模式也能達(dá)到很好的診斷效果。首先采集運(yùn)載火箭的視加速度和角速度信息；之后通過(guò)歸一化神經(jīng)網(wǎng)絡(luò)輸入數(shù)據(jù)，將不同故障模式標(biāo)簽化并對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，建立用于運(yùn)載火箭發(fā)動(dòng)機(jī)故障診斷的神經(jīng)網(wǎng)絡(luò)模型；接著通過(guò)D-S證據(jù)理論融合BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)的診斷結(jié)果，判斷最終的故障模式;最后在確定故障模式的情況下利用滾動(dòng)時(shí)域估計(jì)方法，估計(jì)運(yùn)載火箭發(fā)動(dòng)機(jī)故障下的飛行狀態(tài)特征量。

1 BP神經(jīng)網(wǎng)絡(luò)

BP神經(jīng)網(wǎng)絡(luò)是一種按照誤差反向傳播算法訓(xùn)練的多層前饋網(wǎng)絡(luò)。主要由輸入層、隱含層和輸出層組成[17]，其結(jié)構(gòu)如圖 1所示。

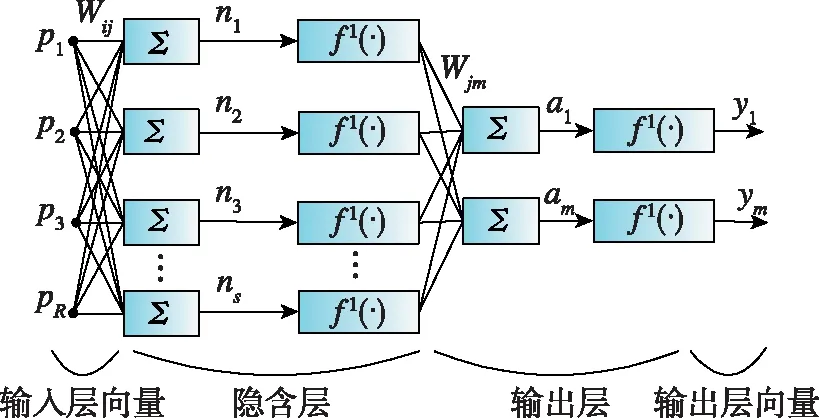
圖1 BP神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)Fig.1 Model structure of BP neural network

BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)包括信號(hào)的前向傳播和誤差的反向傳播兩個(gè)過(guò)程[18]。

BP網(wǎng)絡(luò)三層節(jié)點(diǎn)表示為：輸入節(jié)點(diǎn)xj，隱節(jié)點(diǎn)yi，輸出節(jié)點(diǎn)Ol。輸入節(jié)點(diǎn)與隱節(jié)點(diǎn)間的網(wǎng)絡(luò)權(quán)值為ωij，閾值為θi；隱節(jié)點(diǎn)與輸出節(jié)點(diǎn)間的網(wǎng)絡(luò)權(quán)值為Tli，閾值為θl；輸出節(jié)點(diǎn)的期望輸出為tl。

BP算法的步驟如下[19]：

1)設(shè)置各個(gè)權(quán)值和閾值的初始值；

2)利用式(1)，(2)計(jì)算隱含層和輸出層的輸出

yi=f(∑ωijxj-θi)

(1)

Ol=f(∑Tliyi-θl)

(2)

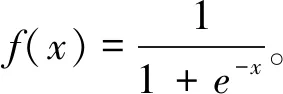
3)計(jì)算輸出節(jié)點(diǎn)與期望輸出之間的誤差

(3)

4)按照公式更新各權(quán)值和閾值

Tli(k+1)=Tli(k)+η(tl-Ol)Ol(1-Ol)yi

(4)

(5)

θl(k+1)=θl(k)+η(tl-Ol)Ol(1-Ol)

(6)

(7)

其中，η為學(xué)習(xí)效率。

5)重新計(jì)算各層的輸出值，當(dāng)誤差小于目標(biāo)誤差時(shí)訓(xùn)練完成，否則重復(fù)上述步驟更新權(quán)值、閾值，直至達(dá)到制定精度或者達(dá)到指定訓(xùn)練次數(shù)。

BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)流程如圖 2所示。

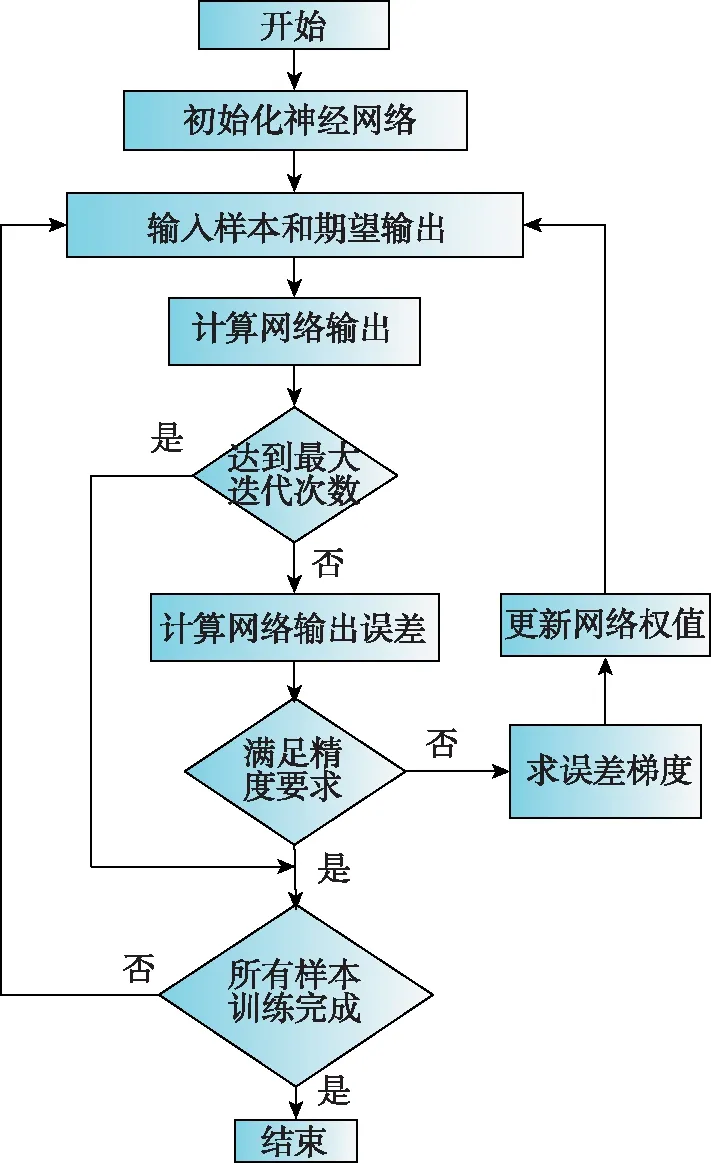
圖2 BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)流程Fig.2 Learning process of BP neural network

2 RBF神經(jīng)網(wǎng)絡(luò)

如圖 3所示，RBF由單隱層的三層前饋網(wǎng)絡(luò)構(gòu)成，其中隱藏層中神經(jīng)元的變換函數(shù)。

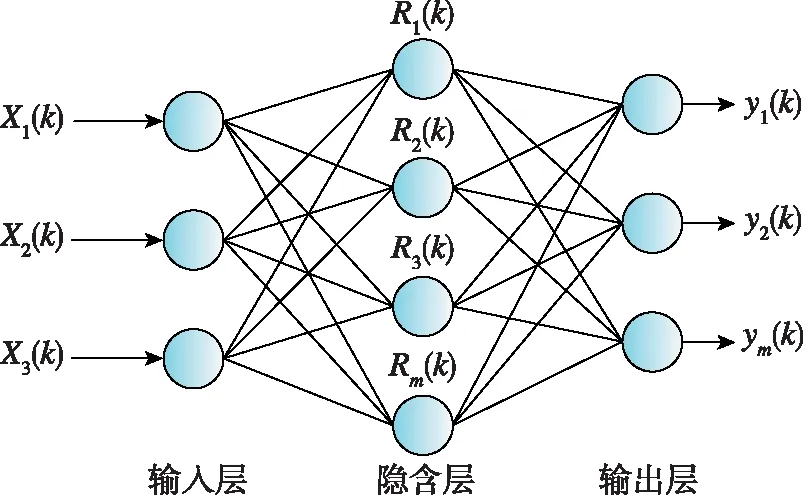
圖3 RBF神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)Fig.3 Model structure of RBF neural network

RBF神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)過(guò)程中，首先采用無(wú)監(jiān)督學(xué)習(xí)確定隱含層中心、擴(kuò)展常數(shù)，最后通過(guò)梯度下降法訓(xùn)練權(quán)值[20]。

假設(shè)t為迭代次數(shù)，則第t次迭代時(shí)聚類中心μ1(t),μ2(t),…,μk(t)，相對(duì)應(yīng)的聚類域?yàn)閃1(t),W2(t),…,Wk(t)。采用K-means聚類算法確定 RBF 神經(jīng)網(wǎng)絡(luò)隱含層的中心和擴(kuò)展常數(shù)的步驟如下[21]：

1)根據(jù)算法應(yīng)用環(huán)境初始化K個(gè)聚類中心，每個(gè)聚類中心的維度和輸入數(shù)據(jù)的維度保持一致；

2)通過(guò)式(8)計(jì)算訓(xùn)練樣本與聚類中心的距離dk，j

(8)

其中，k=1,2,…,K;j=1,2,…,N，N為樣本長(zhǎng)度。

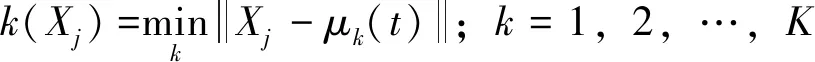
4)通過(guò)式(9)計(jì)算新的聚類中心

(9)

其中，k=1,2,…,K;Nk為第k類中的樣本個(gè)數(shù)。

5)如果μk(t+1)≠μk(t)，轉(zhuǎn)到第2)步，否則聚類結(jié)束，轉(zhuǎn)第6)步執(zhí)行；

6)根據(jù)式(10)計(jì)算RBF神經(jīng)網(wǎng)絡(luò)隱含層神經(jīng)元的擴(kuò)展常數(shù)

σ=κdk

(10)

其中，κ為重疊系數(shù)，dk為第k個(gè)數(shù)據(jù)中心與其余K-1個(gè)數(shù)據(jù)中心距離的最小值，即

(11)

通過(guò)K-means聚類算法確定隱含層神經(jīng)元中心和擴(kuò)展常數(shù)得到網(wǎng)絡(luò)輸出權(quán)值后，通過(guò)梯度下降法訓(xùn)練網(wǎng)絡(luò)權(quán)值。基于梯度下降的權(quán)值訓(xùn)練算法[21]為：

RBF神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的目標(biāo)函數(shù)為

(12)

其中，κj為遺忘因子，誤差信號(hào)ej定義為

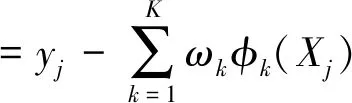
(13)

考慮所有訓(xùn)練樣本和遺忘因子的影響，μk，σk和ωk的調(diào)節(jié)量為

(14)

(15)

(16)

其中，φi(Xi)為第k個(gè)隱節(jié)點(diǎn)對(duì)Xj的輸出，η為學(xué)習(xí)率。

3 D-S證據(jù)理論

D-S證據(jù)理論建立在一個(gè)非空集合Θ上，Θ稱為辨識(shí)框架，在航天器故障診斷中，Θ為一個(gè)故障模式對(duì)應(yīng)的基本故障組成的集合[22]。

定義基本概率分配函數(shù)BPAF(Basic Probability Assignment Function)

m:2Θ→[0,1]

其中，m滿足

m(Φ)=0

(17)

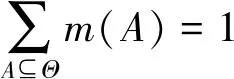
(18)

(A,m(A))稱為證據(jù)體，利用證據(jù)體定義信度函數(shù)和似然函數(shù)

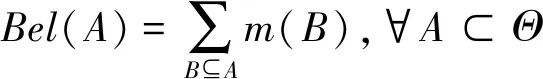
(19)

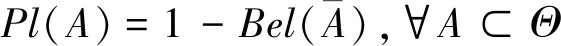
(20)

Bel和Pl表示信度函數(shù)上的上下限值，稱為信度區(qū)間[23]，如圖 4所示。

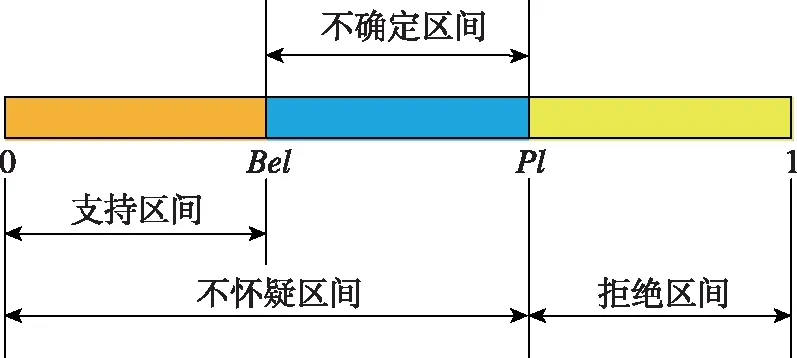
圖4 命題不確定度Fig.4 Uncertainty of proposition

D-S合成規(guī)則是在相同的識(shí)別框架下，給定不同證據(jù)的信度函數(shù)，運(yùn)用合成法則計(jì)算各個(gè)證據(jù)融合之后的信度函數(shù)。

設(shè)Bel1和Bel2分別為同一識(shí)別框架上的兩個(gè)基本概率賦值分配，基本元素分別為A1,A2，…,AK和B1,B2，…,BK，則組合后的基本概率賦值為

(21)

其中，K為沖突因子。

(22)

該合成規(guī)則通過(guò)融合多個(gè)證據(jù)體，可以降低各個(gè)命題之間的沖突，提高診斷結(jié)果的精確性。

4 滾動(dòng)時(shí)域估計(jì)

滾動(dòng)時(shí)域估計(jì)(Moving Horizon Estimation，MHE)可以將估計(jì)問(wèn)題轉(zhuǎn)為優(yōu)化問(wèn)題，同時(shí)將系統(tǒng)的約束條件描述在優(yōu)化問(wèn)題中，通過(guò)在線滾動(dòng)優(yōu)化使其動(dòng)態(tài)滿足[2]。

考慮如下類型的線性離散系統(tǒng)

Xk+1=AXk+GWk

(23)

Zk=CXk+Vk

(24)

其中，Xk為系統(tǒng)狀態(tài)，Zk為測(cè)量輸出，Wk為系統(tǒng)噪聲，Vk為量測(cè)噪聲，A為狀態(tài)轉(zhuǎn)移矩陣，G為輸入矩陣，C為量測(cè)矩陣。

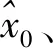
(25)

滿足約束式(26)～(28)。

xk+1=f(xk,uk,wk,k)

(26)

yk=h(xk,k)+vk

(27)

xk∈Xk,wk∈Wk,vk∈Vk

(28)

其中，h(xk,k)為非線性的觀測(cè)函數(shù)。

通過(guò)引入固定的數(shù)據(jù)時(shí)域，可以將帶約束優(yōu)化問(wèn)題的計(jì)算時(shí)域分為兩個(gè)部分

{t1:0≤k≤T-N-1}和{t2:T-N≤k≤T-1}，目標(biāo)函數(shù)定義為式(29)

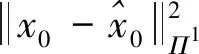
(29)

定義到達(dá)代價(jià)函數(shù)為式(30)

(30)

其中，極小化問(wèn)題滿足約束式(26)～(28)。在此基礎(chǔ)上根據(jù)前向動(dòng)態(tài)規(guī)劃原理，可以將優(yōu)化問(wèn)題等價(jià)為式(31)

ΘT-N(xT-N))

(31)

并且

(32)

滿足約束式(26)～(28)，N為滾動(dòng)時(shí)域窗口長(zhǎng)度。

對(duì)于非線性目標(biāo)運(yùn)動(dòng)模型，使用擴(kuò)展卡爾曼濾波和滾動(dòng)時(shí)域估計(jì)算法得到目標(biāo)的狀態(tài)估計(jì)[25]。

擴(kuò)展卡爾曼濾波的狀態(tài)估計(jì)和狀態(tài)估計(jì)的協(xié)方差矩陣的遞推估計(jì)方程如式(33)，(34)

(33)

(34)

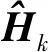
基于擴(kuò)展卡爾曼濾波的滾動(dòng)時(shí)域估計(jì)的狀態(tài)估計(jì)遞推方程如下

(35)

其中，T為當(dāng)前仿真時(shí)刻。

5 基于證據(jù)理論融合和滾動(dòng)時(shí)域估計(jì)的診斷模型

5.1 神經(jīng)網(wǎng)絡(luò)診斷模型

神經(jīng)網(wǎng)絡(luò)的訓(xùn)練誤差是一個(gè)不確定因素。網(wǎng)絡(luò)輸出節(jié)點(diǎn)的輸出被歸一化處理為焦點(diǎn)元素的基本概率值并代入計(jì)算公式

(36)

其中，fi表示故障模式，y(fi)表示神經(jīng)網(wǎng)絡(luò)的輸出結(jié)果，En表示神經(jīng)網(wǎng)絡(luò)樣本誤差。

由于發(fā)動(dòng)機(jī)的構(gòu)型和參數(shù)是固定的，因此，在飛行前可以建立一系列的故障模式，并建立其特征參量模型，這些作為在線軌跡的先驗(yàn)信息。通過(guò)對(duì)飛行狀態(tài)的觀測(cè)來(lái)估計(jì)發(fā)動(dòng)機(jī)故障模式。神經(jīng)網(wǎng)絡(luò)的輸入選取為運(yùn)載火箭的箭體坐標(biāo)系下的三軸視加速度和三軸角速度，為了滿足網(wǎng)絡(luò)對(duì)輸入輸出的要求，須在訓(xùn)練開(kāi)始之前對(duì)數(shù)據(jù)進(jìn)行歸一化處理；輸出選取運(yùn)載火箭的故障模式矩陣。建立故障類型矩陣如表 1所示。

5.2 證據(jù)理論融合診斷模型

由BP神經(jīng)網(wǎng)絡(luò)、RBF神經(jīng)網(wǎng)絡(luò)和D-S證據(jù)理論決策融合系統(tǒng)組成的運(yùn)載火箭發(fā)動(dòng)機(jī)故障模式融合診斷系統(tǒng)如圖 5所示。

識(shí)別框架為

Θ=(ENG11，ENG12，ENG13，ENG14，ENG15，ENG21，ENG22，ENG23，ENG24，ENG25，ENG31，ENG32，ENG33，ENG34，ENG35，ENG41，ENG42，ENG43，ENG44，ENG45)。

定義一種新的基本函數(shù)構(gòu)建方法，以式(37)作為基本概率函數(shù)

(37)

m(Θ)=En

(38)

C(Ai)為BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)的初步診斷結(jié)果，m(Θ)為證據(jù)體的不確定性表示，N為故障類型數(shù)，En表示BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)診斷結(jié)果與期望值的均方差。

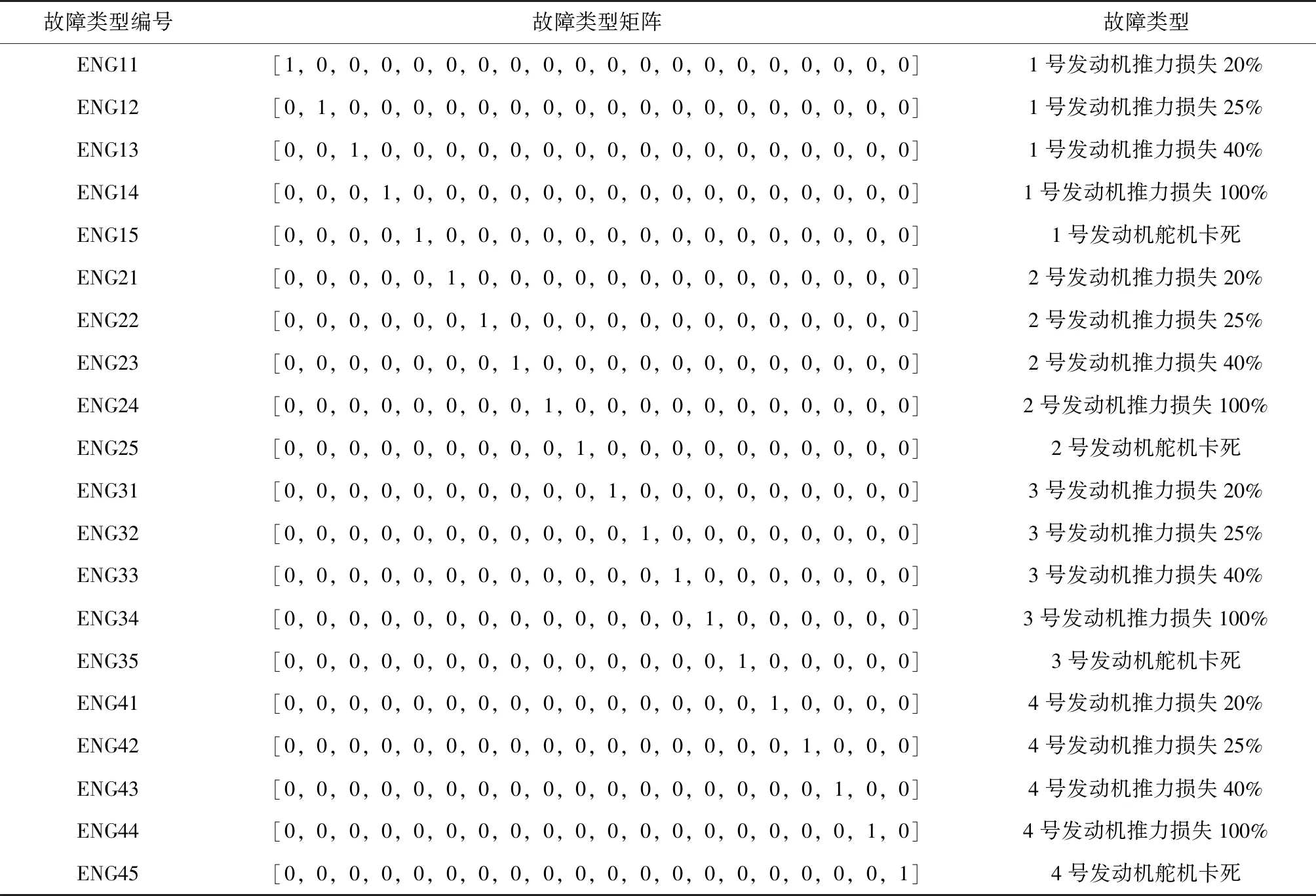
表1 故障類型矩陣

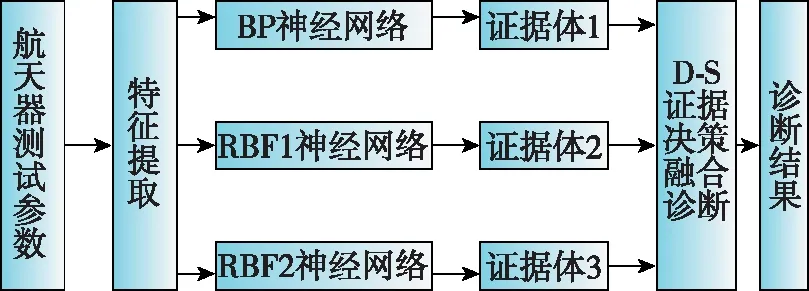
圖5 火箭故障融合診斷系統(tǒng)Fig.5 Fusion diagnosis system of rocket fault

5.3 滾動(dòng)時(shí)域估計(jì)算法模型

系統(tǒng)的狀態(tài)向量為

分別為運(yùn)載火箭在發(fā)射坐標(biāo)系下的加速度、角速度、速度以及位置。

量測(cè)向量為

分別為運(yùn)載火箭彈體坐標(biāo)系下的三軸視加速度。

單個(gè)發(fā)動(dòng)機(jī)推力損失量

Ploss=Pc-Pr

(39)

其中，Pc為發(fā)動(dòng)機(jī)當(dāng)前總推力，Pr為發(fā)動(dòng)機(jī)額定總推力。

單個(gè)發(fā)動(dòng)機(jī)推力損失百分比

(40)

6 仿真算例

6.1 BP網(wǎng)絡(luò)診斷結(jié)果

仿真生成8 000組不同故障模式下的數(shù)據(jù)，利用6 000組數(shù)據(jù)作為訓(xùn)練樣本，2 000組數(shù)據(jù)作為檢測(cè)樣本。

選取BP神經(jīng)網(wǎng)絡(luò)精度為0.001，網(wǎng)絡(luò)學(xué)習(xí)率為0.5，最大訓(xùn)練次數(shù)為300次。隱含層神經(jīng)元個(gè)數(shù)為128的訓(xùn)練效果如圖 6所示。

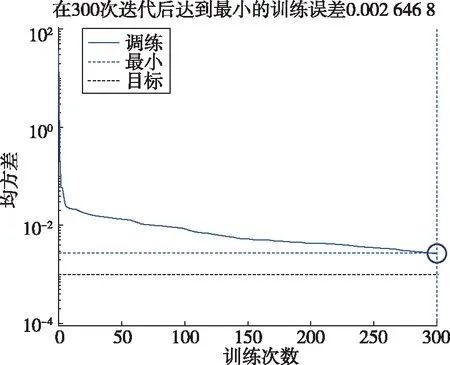
圖6 BP神經(jīng)網(wǎng)絡(luò)訓(xùn)練效果Fig.6 Training performance of BP neural network

對(duì)2 000組測(cè)試數(shù)據(jù)使用訓(xùn)練好的BP神經(jīng)網(wǎng)絡(luò)診斷，診斷正確率為99.1%。

6.2 RBF網(wǎng)絡(luò)診斷結(jié)果

選取RBF神經(jīng)網(wǎng)絡(luò)的目標(biāo)精度為0.01，網(wǎng)絡(luò)傳播速度為1，最大訓(xùn)練次數(shù)為500次。訓(xùn)練效果如圖 7所示。

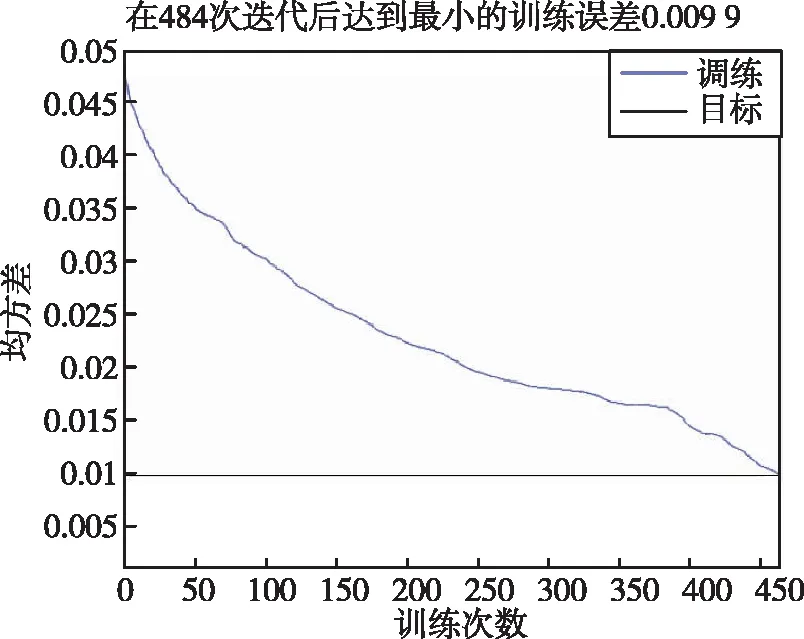
圖7 RBF神經(jīng)網(wǎng)絡(luò)訓(xùn)練效果Fig.7 Training performance of RBF neural network

對(duì)2 000組測(cè)試數(shù)據(jù)使用訓(xùn)練好的RBF神經(jīng)網(wǎng)絡(luò)診斷，診斷正確率為99.2%。

6.3 融合診斷算例

算例1：

假設(shè)故障模式為ENG44，運(yùn)載火箭發(fā)動(dòng)機(jī)在100 s時(shí)，芯一級(jí)四號(hào)發(fā)動(dòng)機(jī)推力下降100%，首先通過(guò)神經(jīng)網(wǎng)絡(luò)和證據(jù)理論綜合決策，判斷運(yùn)載火箭發(fā)動(dòng)機(jī)的故障模式，其次通過(guò)滾動(dòng)時(shí)域估計(jì)對(duì)運(yùn)載火箭推力損失進(jìn)行估計(jì)。

仿真得到100.01 s時(shí)，運(yùn)載火箭的三軸視加速度和三軸角速度數(shù)據(jù)如表 2所示。

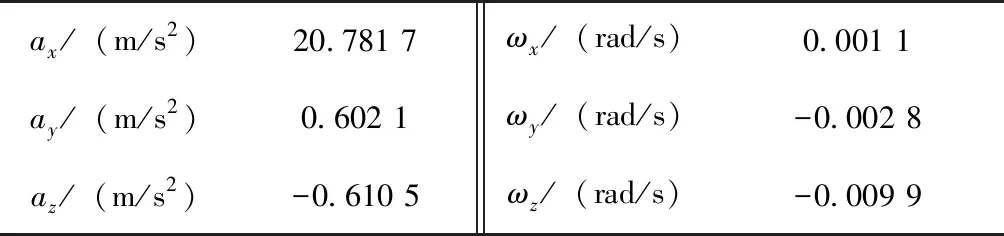
表2 100.01 s時(shí)運(yùn)載火箭部分量測(cè)數(shù)據(jù)

滾動(dòng)時(shí)域估計(jì)窗口長(zhǎng)度N=4。

利用神經(jīng)網(wǎng)絡(luò)進(jìn)行故障模式診斷，神經(jīng)網(wǎng)絡(luò)輸出結(jié)果如表 3所示。

表3 算例1的神經(jīng)網(wǎng)絡(luò)輸出結(jié)果

對(duì)神經(jīng)網(wǎng)絡(luò)的輸出結(jié)果分析，得到火箭故障模式辨識(shí)結(jié)果如表 4所示。

表4 算例1的神經(jīng)網(wǎng)絡(luò)診斷結(jié)果

從表 4可以看到，這組測(cè)試數(shù)據(jù)采用BP神經(jīng)網(wǎng)絡(luò)進(jìn)行診斷時(shí)出現(xiàn)誤診。從診斷結(jié)果的可靠性角度思考，采用不同的神經(jīng)網(wǎng)絡(luò)會(huì)有不同的診斷結(jié)果，不能確定哪種方法的診斷結(jié)果是正確的，因此使用D-S證據(jù)理論融合診斷結(jié)果，確定運(yùn)載火箭故障類別。首先構(gòu)建證據(jù)體，將ENG44故障狀態(tài)下的神經(jīng)網(wǎng)絡(luò)結(jié)果處理得到基本概率分配，經(jīng)D-S證據(jù)理論融合診斷后，結(jié)果如表 5所示。

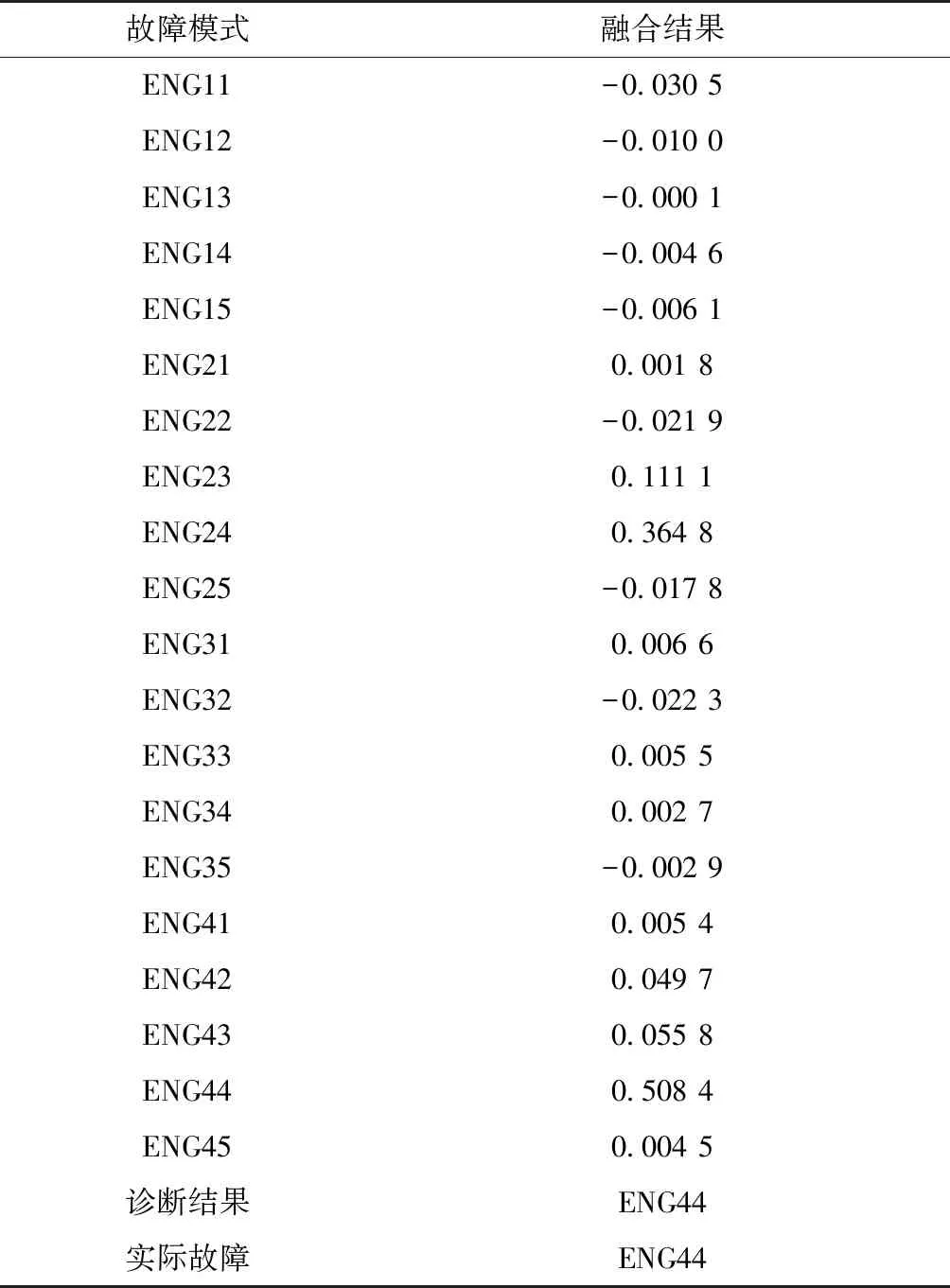
表5 算例1的證據(jù)理論融合診斷結(jié)果

從表 5可以看出，采用D-S證據(jù)理論融合的診斷結(jié)果與實(shí)際故障模式一致。基于滾動(dòng)時(shí)域估計(jì)的運(yùn)載火箭飛行狀態(tài)特征量估計(jì)的仿真結(jié)果如圖8～14所示。

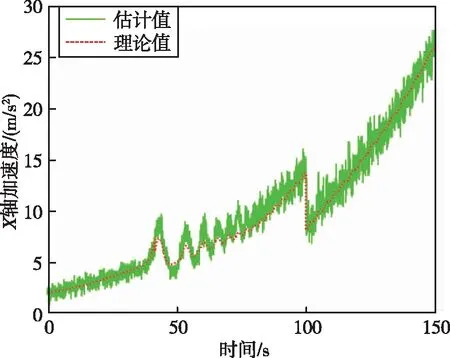
圖8 箭體系下X軸加速度Fig.8 X-axis acceleration in the body coordinate system

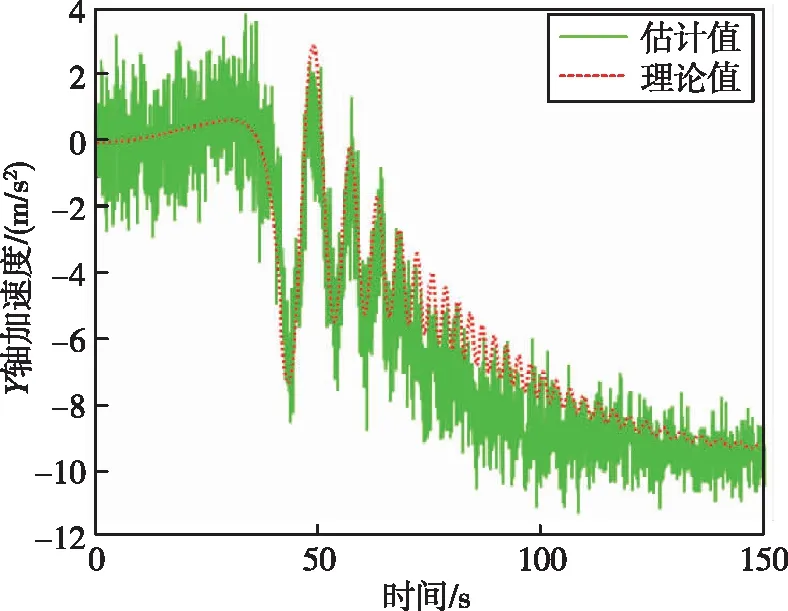
圖9 箭體系下Y軸加速度Fig.9 Y-axis acceleration in the body coordinate system

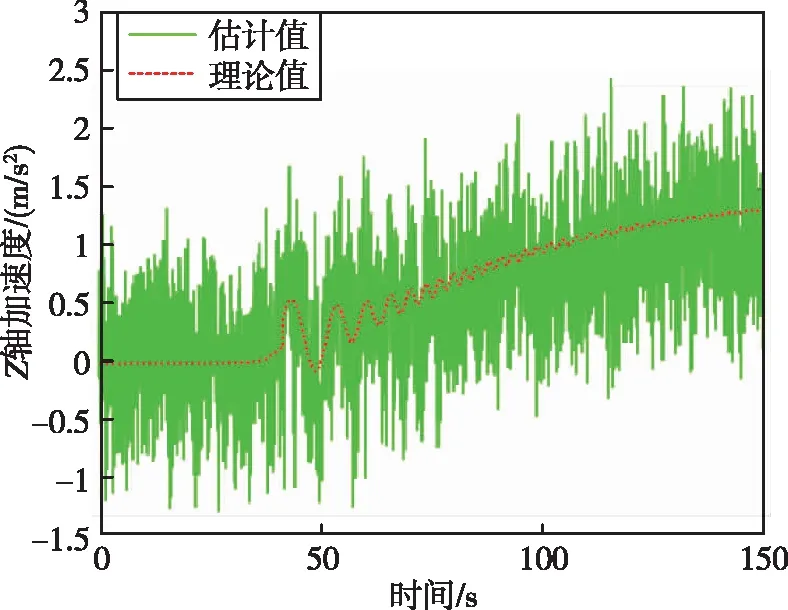
圖10 箭體系下Z軸加速度Fig.10 Z-axis acceleration in the body coordinate system

圖11 箭體系下X軸角速度Fig.11 X-axis angular velocity in the body coordinate system

圖12 箭體系下Y軸角速度Fig.12 Y-axis angular velocity in the body coordinate system

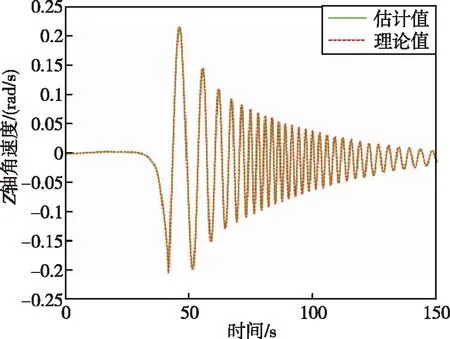
圖13 箭體系下Z軸角速度Fig.13 Z-axis angular velocity in the body coordinate system

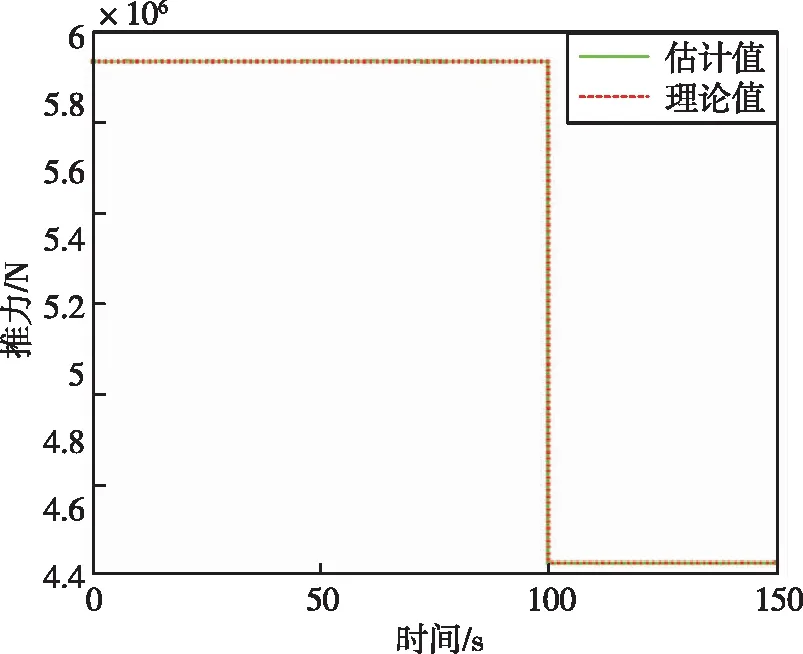
圖14 運(yùn)載火箭總推力Fig.14 Total thrust of rocket

通過(guò)圖 8～13可以看出，滾動(dòng)時(shí)域估計(jì)方法能夠很好地估計(jì)出運(yùn)載火箭故障模式下的三軸加速度以及三軸角速度。通過(guò)圖 14可以看出，在100 s時(shí)，運(yùn)載火箭總推力下降了25%，綜合通過(guò)證據(jù)理論和神經(jīng)網(wǎng)絡(luò)得到的運(yùn)載火箭發(fā)動(dòng)機(jī)故障模式，可以判斷運(yùn)載火箭故障類型為四號(hào)發(fā)動(dòng)機(jī)在100 s時(shí)推力下降了100%，符合仿真設(shè)定的故障模式。

算例2：

假設(shè)故障模式為ENG15，運(yùn)載火箭在80 s時(shí)，芯一級(jí)一號(hào)發(fā)動(dòng)機(jī)舵機(jī)卡死，通過(guò)神經(jīng)網(wǎng)絡(luò)和證據(jù)理論綜合決策，判斷運(yùn)載火箭發(fā)動(dòng)機(jī)的故障模式。

仿真得到80.01 s時(shí)，運(yùn)載火箭的三軸視加速度和三軸角速度數(shù)據(jù)如表 6所示。

表6 80.01 s時(shí)運(yùn)載火箭部分量測(cè)數(shù)據(jù)

利用神經(jīng)網(wǎng)絡(luò)進(jìn)行故障模式診斷，神經(jīng)網(wǎng)絡(luò)輸出結(jié)果如表 7所示。

表7 算例2的神經(jīng)網(wǎng)絡(luò)輸出結(jié)果

對(duì)神經(jīng)網(wǎng)絡(luò)的輸出結(jié)果進(jìn)行分析，得到火箭故障模式辨識(shí)結(jié)果如表 8所示。

表8 算例2的神經(jīng)網(wǎng)絡(luò)診斷結(jié)果

從表8可以看到，這組測(cè)試數(shù)據(jù)采用RBF2神經(jīng)網(wǎng)絡(luò)進(jìn)行診斷時(shí)出現(xiàn)誤診，進(jìn)而使用D-S證據(jù)理論融合診斷結(jié)果，確定運(yùn)載火箭故障類別。首先構(gòu)建證據(jù)體，將ENG15故障狀態(tài)下的神經(jīng)網(wǎng)絡(luò)結(jié)果處理得到基本概率分配，經(jīng)D-S證據(jù)理論融合診斷后，結(jié)果如表 9所示。

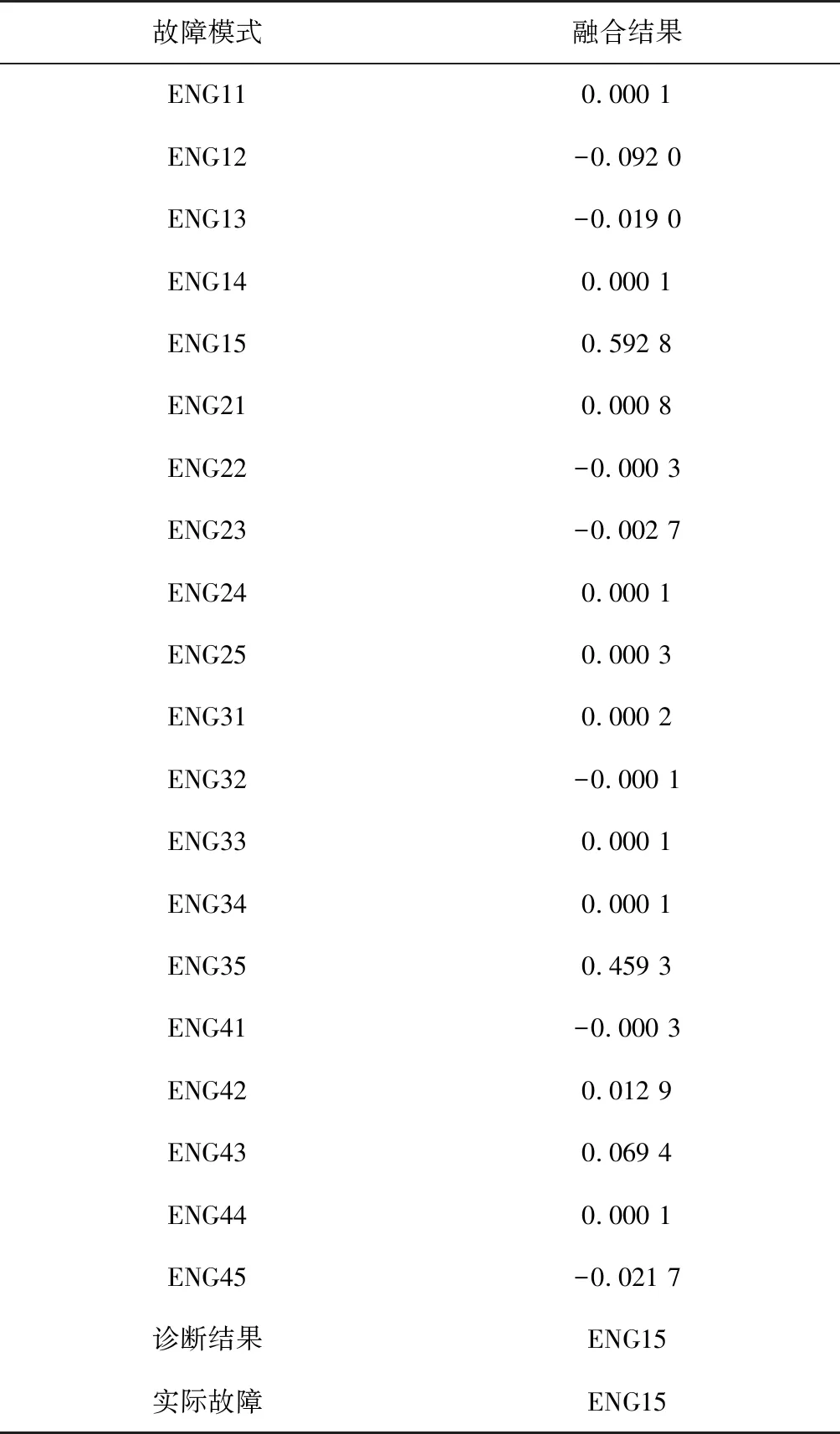
表9 算例2的證據(jù)理論融合診斷結(jié)果

從表9可以看出，采用D-S證據(jù)理論融合診斷的故障模式與實(shí)際故障模式一致。

基于神經(jīng)網(wǎng)絡(luò)和D-S證據(jù)理論，對(duì)2 000組測(cè)試數(shù)據(jù)進(jìn)行檢測(cè)，辨識(shí)正確率為99.4%。

7 結(jié)論

本文以運(yùn)載火箭動(dòng)力系統(tǒng)故障為背景，研究了基于BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)的運(yùn)載火箭發(fā)動(dòng)機(jī)故障模式診斷方法，并提出通過(guò)D-S證據(jù)融合理論綜合神經(jīng)網(wǎng)絡(luò)的診斷結(jié)果，確定故障類型后通過(guò)滾動(dòng)時(shí)域估計(jì)方法估計(jì)火箭飛行狀態(tài)特征量。通過(guò)仿真案例表明神經(jīng)網(wǎng)絡(luò)對(duì)于故障模式的辨別有較高的正確率，再通過(guò)證據(jù)理論能夠有效提高診斷的準(zhǔn)確率，滾動(dòng)時(shí)域估計(jì)方法能夠在線估計(jì)火箭飛行狀態(tài)特征量，以便對(duì)火箭故障進(jìn)行更精準(zhǔn)的判斷。該方法還可應(yīng)用于運(yùn)載火箭其他模式的故障診斷中，為火箭故障診斷提供了新方法。