經(jīng)歷實(shí)踐活動(dòng)發(fā)展思維能力

孫文三

摘 要：課堂教學(xué)不應(yīng)該是數(shù)學(xué)學(xué)習(xí)的終點(diǎn)，而應(yīng)該是學(xué)生積極主動(dòng)學(xué)習(xí)的新起點(diǎn)。教師能引導(dǎo)學(xué)生動(dòng)起手來，學(xué)生能不怕犯錯(cuò)誤，大膽質(zhì)疑，養(yǎng)成勇于嘗試探索的精神，這應(yīng)該成為數(shù)學(xué)家常課堂的主旋律。

關(guān)鍵詞：動(dòng)手;動(dòng)腦;玩轉(zhuǎn);圓錐體

圓柱和圓錐是生活中非常容易遇到的幾何體，是小學(xué)立體圖形學(xué)習(xí)的重要部分。在教學(xué)中，結(jié)合實(shí)物直觀圖“去看”固然是展開探索活動(dòng)的有效途徑之一，而鼓勵(lì)并引導(dǎo)學(xué)生動(dòng)起手來主動(dòng)探究、邊玩邊思考，無疑更能激發(fā)學(xué)生的持久興趣。以下結(jié)合日常課堂教學(xué)，重點(diǎn)以圓錐體為探討對(duì)象。

一、找一找，從自由觀察到重點(diǎn)聚焦

孩子天性愛玩。會(huì)玩的小孩無形中玩出了成長(zhǎng)的智慧，而不會(huì)玩的小學(xué)生則玩出了麻煩，更不可能玩轉(zhuǎn)數(shù)學(xué)。在學(xué)習(xí)圓錐體之前，我布置了一項(xiàng)神秘的家庭作業(yè)，即讓學(xué)生回家盡可能多地找一找家中的圓錐體，能帶來的則帶到課堂，不能帶來的可以繪制草圖。

（一）圓錐體是有溫度的

第二天的課堂成了孩子們“曬寶”的大比拼。學(xué)生甲帶來了自己吃過的蛋卷冰激凌筒，上面還散發(fā)著滿滿的香味;學(xué)生乙的爸爸是一位辛勤的瓦工師傅，他帶來了爸爸砌墻用的沉甸甸的鉛錘;學(xué)生丙則展示了一幅草圖，大體形狀是書房臺(tái)燈燈泡上面圓錐形的燈罩。學(xué)生自己動(dòng)手找到的圓錐體，有味、有情、有形、有分量，這樣的圓錐體才是有溫度、有故事的。

（二）圓錐體是有生命力的

學(xué)生們是非常善于觀察的，教師往往只需要給他們一點(diǎn)點(diǎn)“啟示”，就能極大地激發(fā)他們的觀察力、想象力。有學(xué)生帶來了兒時(shí)玩過的陀螺，雖然陳舊，但是殘留自己玩過的痕跡;有學(xué)生出示了自己剛刨過的鉛筆尖，剛被削出的小小的圓錐體近在手中;其中有一位學(xué)生笑著說，“撐開的雨傘”也是一個(gè)近似的圓錐體，多么動(dòng)感，多么飽滿，多么可愛的圓錐體。學(xué)生們經(jīng)過這一番比拼，驀然發(fā)現(xiàn)原來傳說中的圓錐體并不陌生，它們就時(shí)刻潛藏在我們的生活之中。今天的課堂學(xué)習(xí)，我們只是有重點(diǎn)地把目光聚焦于此而已。

二、轉(zhuǎn)一轉(zhuǎn)，從直觀判斷到理智分析

曬寶結(jié)束，質(zhì)問開始。我提出若干問題：這些所謂的圓錐體到底都長(zhǎng)啥樣？哪里有“圓”？哪兒有“錐”？“體”“面”怎回事？

首先，我給四人小組每組發(fā)放一根小木棒、一張卡紙，然后拿出一個(gè)小木棒，他們面面相覷，不知道要做什么。當(dāng)我把一張直角三角形卡紙的一條直角邊固定在木棒上，他們開始猜測(cè)我的行為動(dòng)機(jī)。此時(shí)我卻停下來了，鼓勵(lì)學(xué)生們?nèi)ダ^續(xù)下面的游戲，讓他們旋轉(zhuǎn)木棒、決定直角邊的長(zhǎng)短、裁剪直角三角形的大小。

或快或慢，到底轉(zhuǎn)出了什么圖形？轉(zhuǎn)動(dòng)的圖形中，各個(gè)特征在哪？有無神奇的變化？諸如此類的問題交給各組討論，并請(qǐng)代表發(fā)言，相互交流玩轉(zhuǎn)的圓錐體的勞動(dòng)收獲。

三、剪一剪，從綜合認(rèn)知到課外拓展

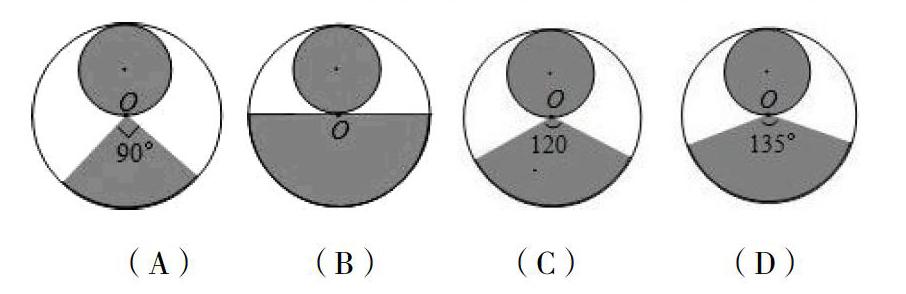
學(xué)過圓柱體的表面積計(jì)算法后，面對(duì)圓錐體的展開圖，有學(xué)生理直氣壯地問我，怎么書本上沒有圓錐體表面積的求法？難道無法求解嗎？我沒有直接回答能或不能，只是給他提供了一道選擇題，題目如下：從一張圓形紙板剪出一個(gè)小圓形和一個(gè)扇形，分別作為圓錐體的底面和側(cè)面，下列的剪法恰好配成一個(gè)圓錐體的是（）。

他在仔細(xì)觀察、對(duì)比之后，還是不確定，但憑感覺他很慎重地選擇了D。我沒有給他提供正確答案，只是撒了個(gè)善意的謊言說，老師也懵了。我知道他不服輸?shù)膭艃菏浅隽嗣摹Ｎ遗呐乃募绨蛘f，你可以回去剪一剪、做一做嘛！

第二天一大早，他就跑到我辦公室說他找到答案了，而且還攥著拼湊成功的得意作品。我笑著說，應(yīng)該是“剪”到答案了。而且在剪拼的操作中，他還發(fā)現(xiàn)——小圓的周長(zhǎng)與扇形的弧線長(zhǎng)必須相等，才能搭配成一個(gè)完整的圓錐體。

四、倒一倒，從對(duì)比關(guān)聯(lián)到建立模型

課本刻意把圓柱與圓錐放在一起編排教學(xué)，既顯示出編著者的良苦用心，也表現(xiàn)出圓柱與圓錐二者之間確實(shí)存在諸多的對(duì)比關(guān)聯(lián)，利于學(xué)生的對(duì)比學(xué)習(xí)。

（一）從古籍中領(lǐng)略先人智慧

實(shí)際上，我們先人早就研究過如何計(jì)算物體體積。《九章算術(shù)》記載圓柱體體積計(jì)算“周自相乘，以高乘之，十二而一”;圓錐體體積計(jì)算“下周自乘，以高乘之，三十六而一”。通俗地說，即圓柱體體積計(jì)算方法即底面周長(zhǎng)的平方乘高，再乘十二分之一，圓錐體體積即底面周長(zhǎng)的平方乘高，再乘三十六分之一。

（二）從實(shí)驗(yàn)中感知體積關(guān)系

準(zhǔn)備圓柱和圓錐形容器各一，等底等高。先用沙子填滿圓錐形容器，再倒入圓柱形容器，觀察需要幾次才能填滿。利用這個(gè)直觀的小實(shí)驗(yàn)，我們能很清楚地看到，三次正好能填滿。所以，圓錐體的體積是與它等底等高的圓柱體體積的1/3。

這種關(guān)系，也可以通過切一切來感知。例如將底面直徑長(zhǎng)2厘米，高3厘米的圓柱體橡皮泥切成圓錐體，這個(gè)圓錐體最大體積是多少？這種通過切割處理，能非常形象地揭示出兩者的體積關(guān)系。

（三）從模型中發(fā)展思維水平

建立圓錐模型不只是一句口號(hào)，也不是一個(gè)簡(jiǎn)單的行為動(dòng)作。這種模型不只是一個(gè)實(shí)實(shí)在在的圓錐物體，而是在學(xué)生的思維深處抽象出一個(gè)可大可小、可合可分、動(dòng)感十足的活圓錐。

生活中處處都有圓錐體的影子，只有做個(gè)有心人，我們完全可以輕松地將身邊的實(shí)物抽象為圓錐問題，進(jìn)而感知立體圖形在生活中的重大價(jià)值。反過來，我們也可以別有用心地將圓錐問題貼近生活，在動(dòng)手玩耍中將課內(nèi)看似枯燥干癟的理論知識(shí)注入更多的生活氣息，迫使理論更接地氣。如此這般動(dòng)手又動(dòng)腦，學(xué)生玩轉(zhuǎn)的又何止是圓錐體。

參考文獻(xiàn)

[1]楚平.數(shù)學(xué)教師教學(xué)用書[M].江蘇鳳凰教育出版社，2016.

[2]閆禎.有效學(xué)習(xí)指導(dǎo)[M].陜西師范大學(xué)出版社，2013.

[3]裴娣娜.教育研究方法導(dǎo)論[M].安徽教育出版社，2008.

[4]余文森.名師怎樣觀察課堂[M].上海：華東師范大學(xué)出版社，2009.

[5]教育部制訂.小學(xué)數(shù)學(xué)新課程標(biāo)準(zhǔn)[M].北京師范大學(xué)出版社，2015.

[6]王策三.教學(xué)論稿[M].人民教育出版社，2005.

[7]黃希庭，鄭涌.心理學(xué)十五講[M].北京大學(xué)出版社，2005.