基于自適應網格及響應面模型的永磁電機多目標優化
劉曉宇,袁 彬,戴太陽,殷 毅
(重慶大學 輸配電裝備及系統安全與新技術國家重點實驗室,重慶 400045)
0 引 言
永磁電機由于具有噪聲低、運行效率高、使用壽命長等優勢,逐漸成為電氣自動化設備體系的重要組成。隨著永磁電機在工業中作為如輪轂電機、風機等受到廣泛應用,高效、節能目前正成為永磁電機的重要發展方向。
永磁電機設計中,為了提高電機性能和可靠性,需要對結構進行優化。如分析槽口寬度、極槽配合、磁鋼參數對轉矩波動的影響[1];分析極槽配合和磁鋼參數對于紋波轉矩和齒槽轉矩的影響[2]。有限元法是電機結構優化中廣泛使用的數值方法之一,采用網格離散的方式,可以準確模擬電機內部的電磁場、溫度場等分布情況。應用于電機結構優化時,有限元法通過分析包含多個對象的設計區域內場的分布情況來求解優化問題。這些對象的結構可能是復雜的甚至具有時變特性[3],在這種情況下,需要在優化過程的每個時間步長重新生成有限元網格,這需要耗費大量的計算時間。解決這類問題的方法之一是開發一種新的網格結構,使網格重構更加方便或不需要對全部網格進行重構。目前,更新網格的方法主要是通過利用幾何參數更新網格節點坐標。另一種方法是通過求解彈性方程[4]或者拉普拉斯方程[5],獲得新的節點坐標來重構部分區域的網格。然而,這種類型的部分網格節點重新映射方法仍然是相當耗時的,而且構成的網格單元甚至可能產生折疊。基于徑向基函數插值的網格重構法[6]和基于優化的移動網格策略[7]等方法,其算法復雜,難以實際應用于仿真分析。參數化網格技術[8]可以通過將節點的坐標表示為一組向量基下的展開系數,實現網格的快速二維變形。然而,這種方法適應于較小的形變,對于幾何變形較大的情況會出現網格重疊。因此,為了能有效解決電機結構優化過程中有限元法網格重構的復雜性,需要一種適用于各種范圍形變的網格重構方法,降低有限元計算的工作量,提高計算效率。
本文提出一種基于雙層結構的有限元網格,即形變對象處于上層網格,該對象周圍區域位于背景網格。在優化部件存在較大尺寸變化的優化過程中,采用這種自適應雙層網格結構,可以避免網格的變形,不需要重新計算所有網格節點坐標,從而減少網格重構所需的計算量。為了進一步減小計算量,提高結構優化的效率,本文采用基于移動最小二乘法響應面模型,模擬目標函數與不同輸入因素之間的關系。采用有限元仿真結果校驗調整響應面模型參數,使響應面模型充分考慮數學描述和物理原則之間的關系,使模型更接近實際結構,從而提高響應面模型的精度[9]。
本文以一臺48槽22對極表貼式永磁同步電機(電機Ⅰ)和一臺18槽22對極徑向磁通調制電機(電機Ⅱ)為對象,通過有限元仿真軟件建立模型,以磁鋼厚度、鐵心軸向長度、定轉子內外徑等為優化參數,對電機轉矩與溫升, 利用自適應雙層網格有限元方法,建立樣本數據組,構建并校驗基于移動最小二乘法的響應面模型,將建立的響應面模型應用于電機結構的多目標優化問題,證明了所提出的方法能有效優化電機的性能。
1 數值計算方法
1.1 自適應雙層網格有限元方法
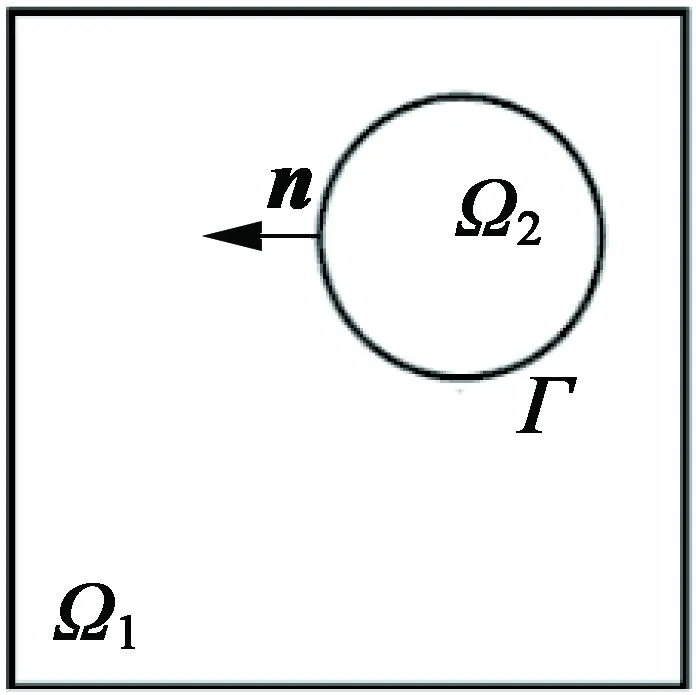
圖1 設計區域及邊界示意圖
-Δui=fi在Ωi里i=1,2
(1)
[un]=0 在Γ上
(2)
u=0 在Γ上
(3)
自適應雙層網格的構建方法如下:
(1) 如圖2(a)所示,在優化部件及整個背景區域劃分初始網格。在優化過程中,背景網格將保持不動,與此同時,上層網格與背景網格的相對關系將保持不變。
(2) 如圖2(b)所示,在背景網格上確定發生兩層網格交疊的單元。
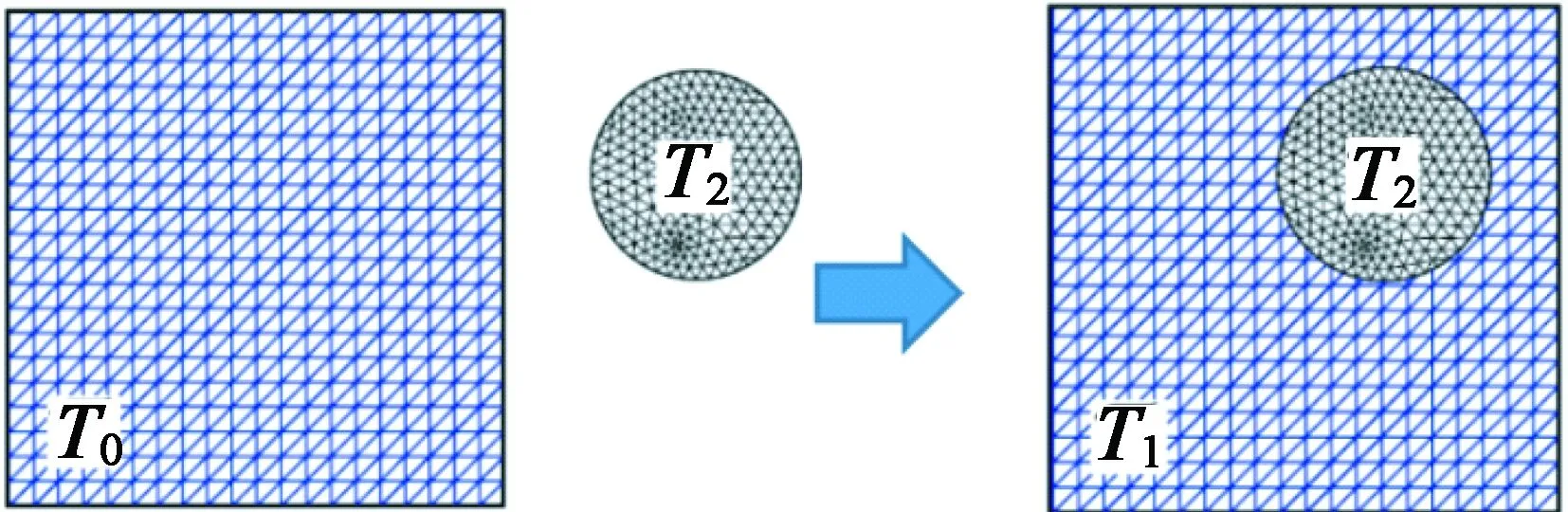
(a) 初始網格劃分
(3) 獲得交疊單元的單元信息,如節點坐標、交點坐標、節點數、單元數、單元邊界條件等,這些信息將被儲存起來供后續調用。
(4) 根據交疊單元的信息,在背景網格重新構建多邊形單元替代交疊單元。
根據交疊單元的信息,進行有限元單元計算及后處理,標量值函數u(x)的插值方案如下式:
(4)
(5)
(6)
式中:φi(x)為構成插值矩陣的系數;ξi(x)為與角度和系數有關的變量;ri=ri(x)是個體p和pi之間的歐式距離,其中角度αi如圖3所示。整個網格系統分為三種類型的單元:背景網格單元、上層網格單元、交疊網格單元。不同區域的單元分析可以單獨計算。圖4為雙層網格交疊部位示意圖。
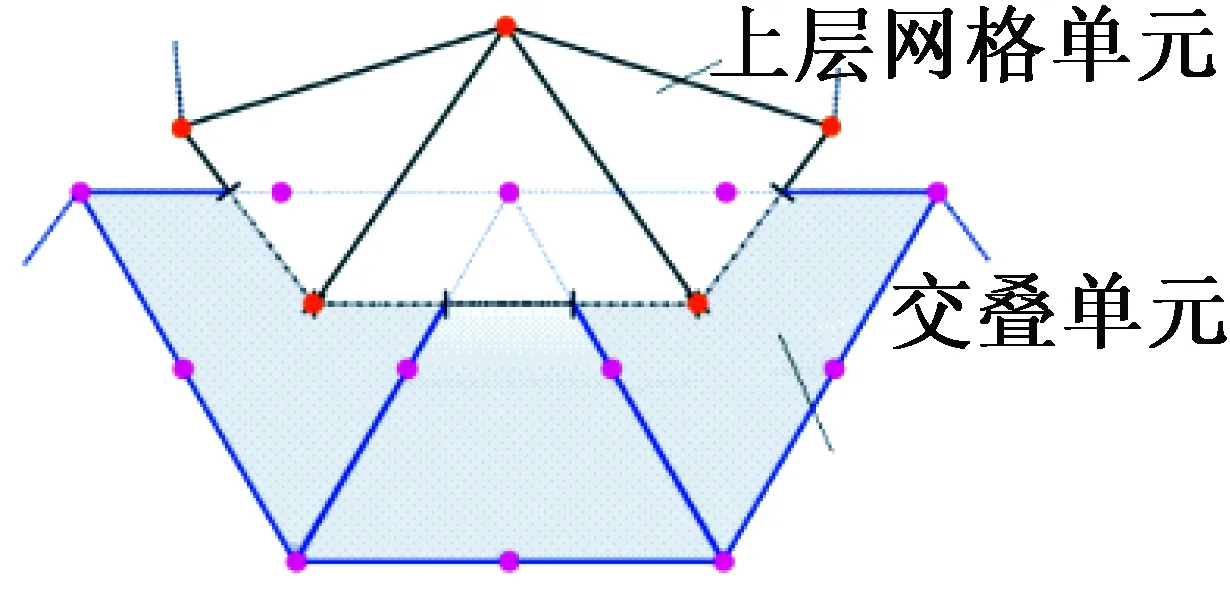
圖4 雙層網格交疊部位示意圖
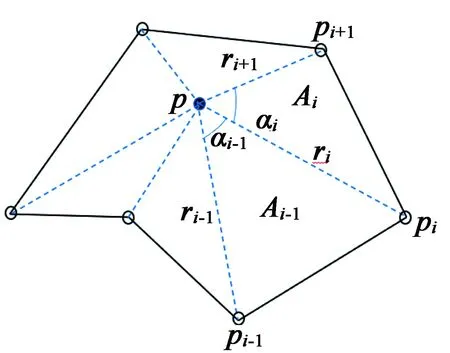
圖3 多邊形單元的平均值坐標
1.2 響應面模型
本文所采用的改進的響應面模型是基于移動最小二乘法以及先驗信息。移動最小二乘法用于搜尋響應面模型的有效系數,先驗信息用于構建可靠的響應面模型。最小二乘法函數L(x)定義為如下帶權重的誤差之和:
(7)
式中:y為n×1目標函數值向量;n為實驗次數;X為n×p獨立變量水平矩陣;ωi是第i個響應值權重;x是近似位置向量;W(x)為位置x處目標函數的權重矩陣。特別的,在移動最小二乘法中,W(x)是目標函數權重的對稱矩陣。為了得到最小化的L(x),移動最小二乘估計方法如下式:
(8)
b(x)=[XTW(x)X]-1XTW(x)y
(9)
1.3 氣隙導熱系數和對流換熱系數
在電機的氣隙部位,對流傳熱是通過如下等效傳熱假設實現的:當靜止的空氣轉移的熱量等于向流動的空氣傳遞的熱量,轉子的旋轉可以看作一個穩定的過程,在氣隙,空氣流動的傳熱能力由靜止的導熱系數表示。有效導熱系數的計算方法如式(10)~式(11)所示[4]。
轉子表面的對流換熱系數:
(10)
式中:υ為轉子表面的旋轉速度。槽內絕緣的等效導熱系數:
(11)
式中:λi和δi分別為不同絕緣材料的平均導熱系數和等效厚度。
2 數值實驗
2.1 電機結構及參數
本文采用的永磁體材料為N35SH,最大耐熱溫度為150 ℃, 剩磁為 1.14 T,矯頑力為860 kA/m。
圖5(a)為傳統的48槽22對極分數槽永磁同步電機(電機Ⅰ),相關初始參數如表1所示。圖5(b)

表1 電機Ⅰ的主要結構參數
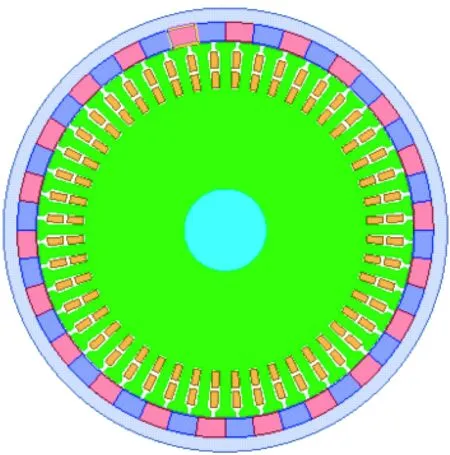
(a) 永磁同步電機(電機Ⅰ)
為18槽22對極徑向磁通調制電機(電機Ⅱ),電機Ⅱ具有一個氣隙,相關初始參數如表2所示。
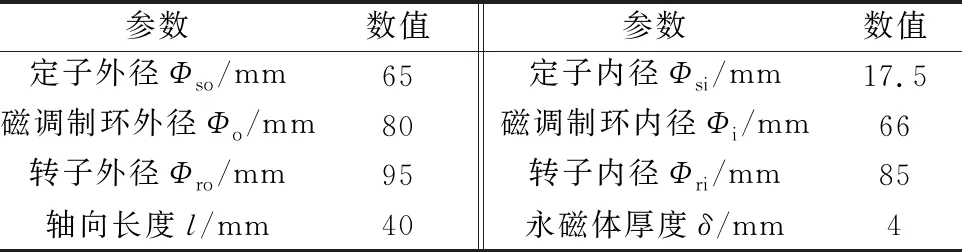
表2 電機Ⅱ的主要結構參數
2.2 響應面模型
為了將所提出的方法應用于電機結構的優化,本文設計并優化了分數槽永磁同步電機和徑向磁通調制電機。優化問題可以用下式:
(12)
式中:f(X)={f1,f2} 表示目標函數,f1為轉矩,f2為溫升;gi(X)為約束條件,m為約束條件數量;X={x1,x2,…,xn}為一系列結構參數,n為參數數量。本文通過調節兩臺電機的繞組電流來控制溫升。采用基于移動最小二乘法的電流-溫升關系模型,該模型可以替代優化過程中的有限元仿真,能夠較大地減少優化問題的計算時間。電機多目標優化的結果將用于驗證提出的優化方法的可行性。式(13)將用于驗證結果的準確性。
(13)
式中:N為對比測試中隨機樣本點的數量。本文中,溫升的響應面模型與有限元比較測試中,選取了15個隨機樣本點,轉矩的響應面模型與有限元比較測試中選取了20個隨機樣本點。
以溫升為例,通過磁場分析得到電機各部件的損耗后利用熱分析計算出兩臺電機的溫升。對電機Ⅰ、電機Ⅱ采用自適應雙層網格有限元方法模擬電磁場分布情況,獲得電機的溫升情況,通過調節繞組電流進行采樣,對樣本點采用基于移動最小二乘法的響應面模型建立電流-溫升關系模型,得到的電機Ⅰ、電機Ⅱ溫度模型分別如下:
yⅠ=0.000 197 32x3-0.030 456x2+2.519 1x
(14)
yⅡ=0.000 052 001x3-0.004 603x2+0.888x
(15)
電機Ⅰ、電機Ⅱ溫升隨電流變化及輸出轉矩的響應面模擬值與有限元對比如圖6、圖7所示。由此可見,本文采用的響應面模型對溫升及轉矩的模擬較為準確,可以作為多目標優化問題的目標函數,替代迭代尋優中的有限元分析。
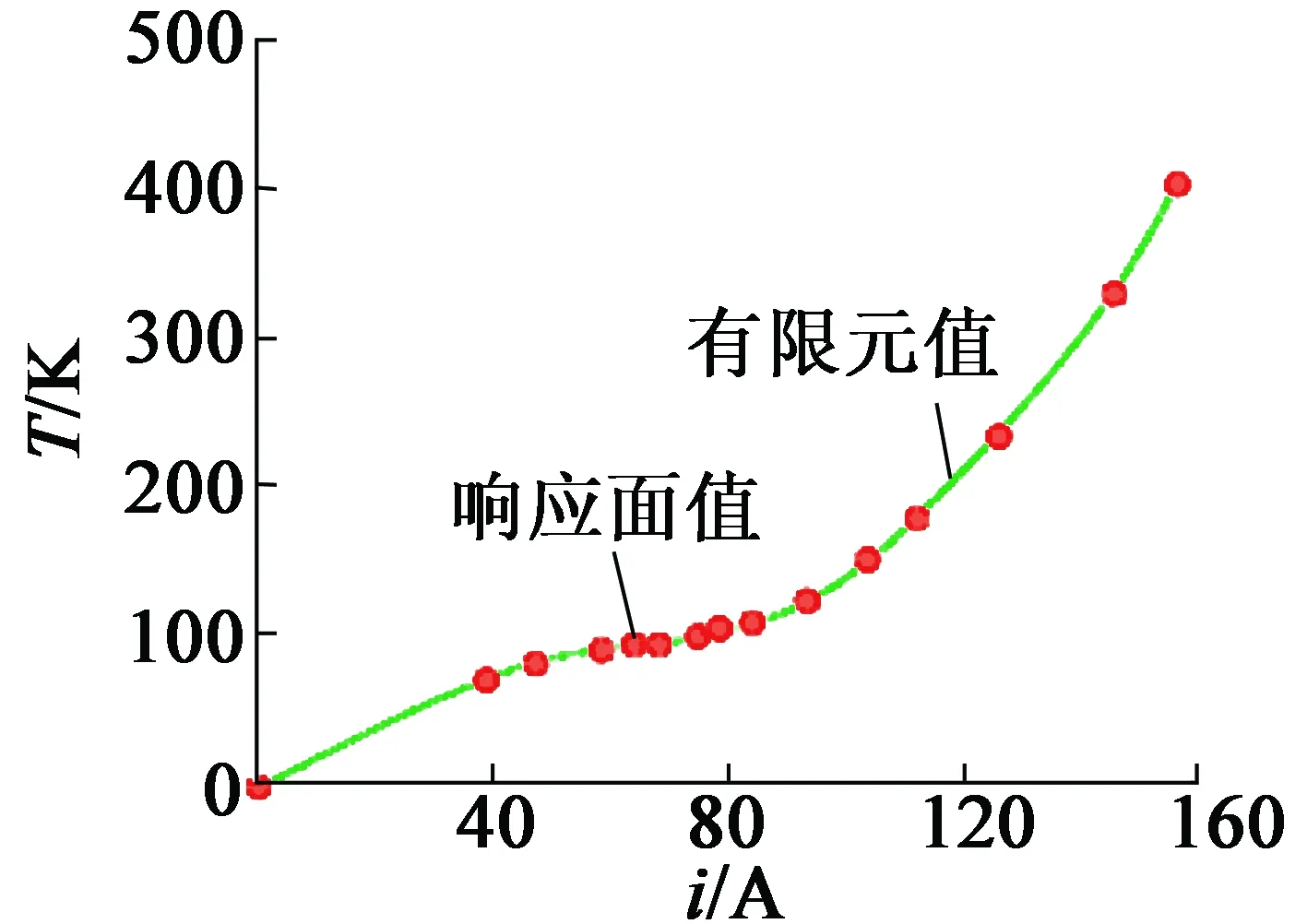
(a) 電機Ⅰ
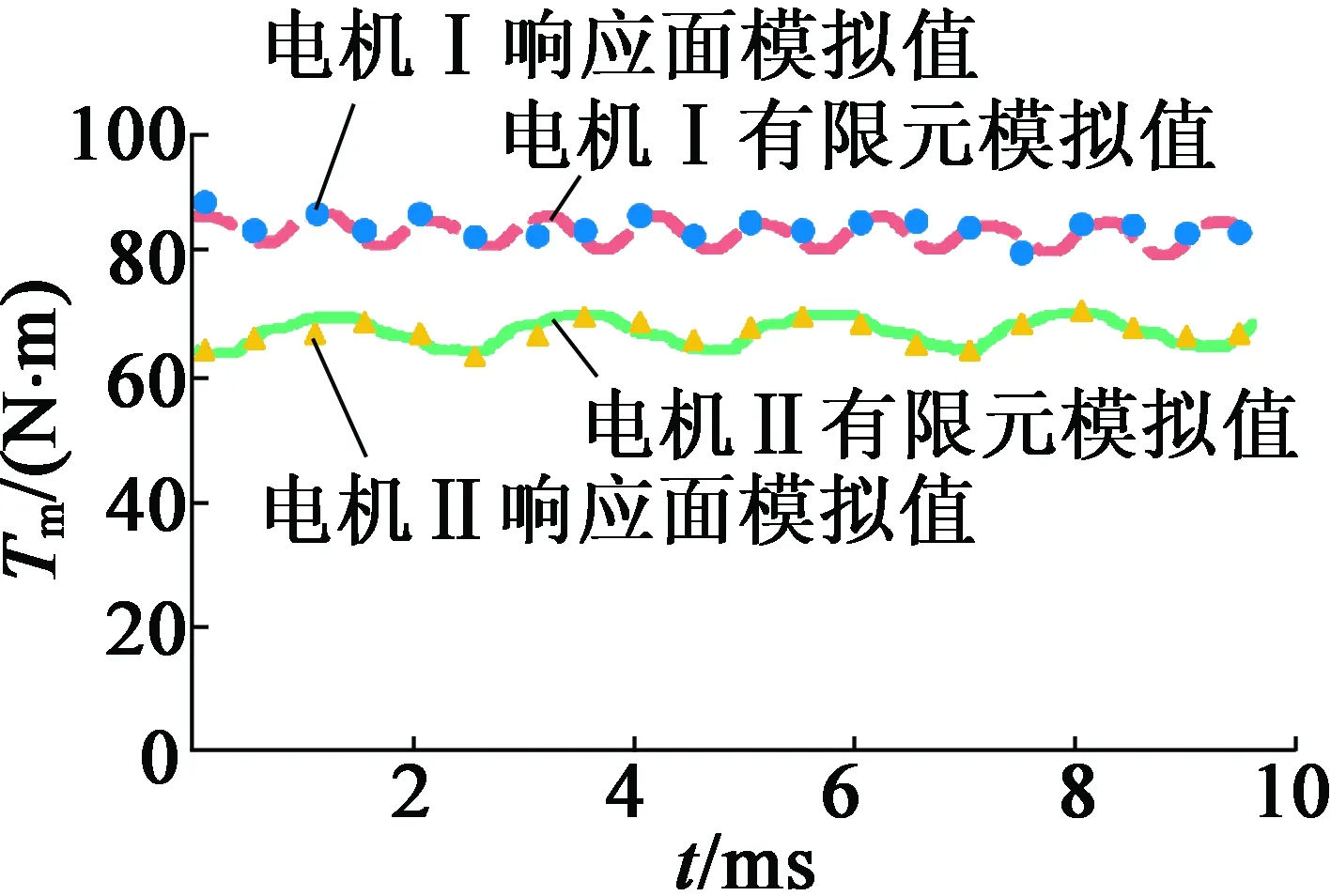
圖7 轉矩的響應面模型與有限元法比較
2.3 多目標優化
采用本文提出的自適應雙層網格有限元法,結合基于移動最小二乘法的響應面模型,依據多目標遺傳算法對電機Ⅰ、電機Ⅱ進行結構優化。優化后電機的磁通分布如圖8所示。兩種電機的最高溫升都在定子繞組內。電機Ⅰ、電機Ⅱ的定子和繞組的溫度分布如圖9所示。仿真結果顯示,優化后的電機結構磁通分布合理,溫度處于永磁體耐熱范圍內。
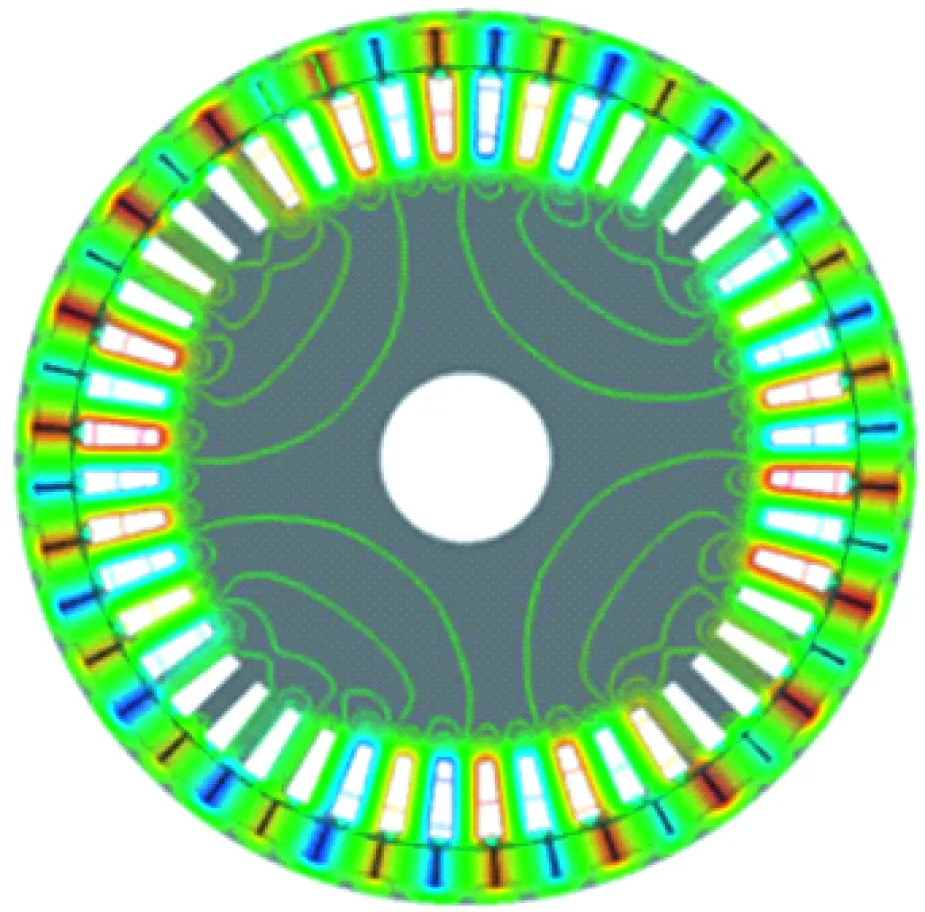
(a) 電機Ⅰ
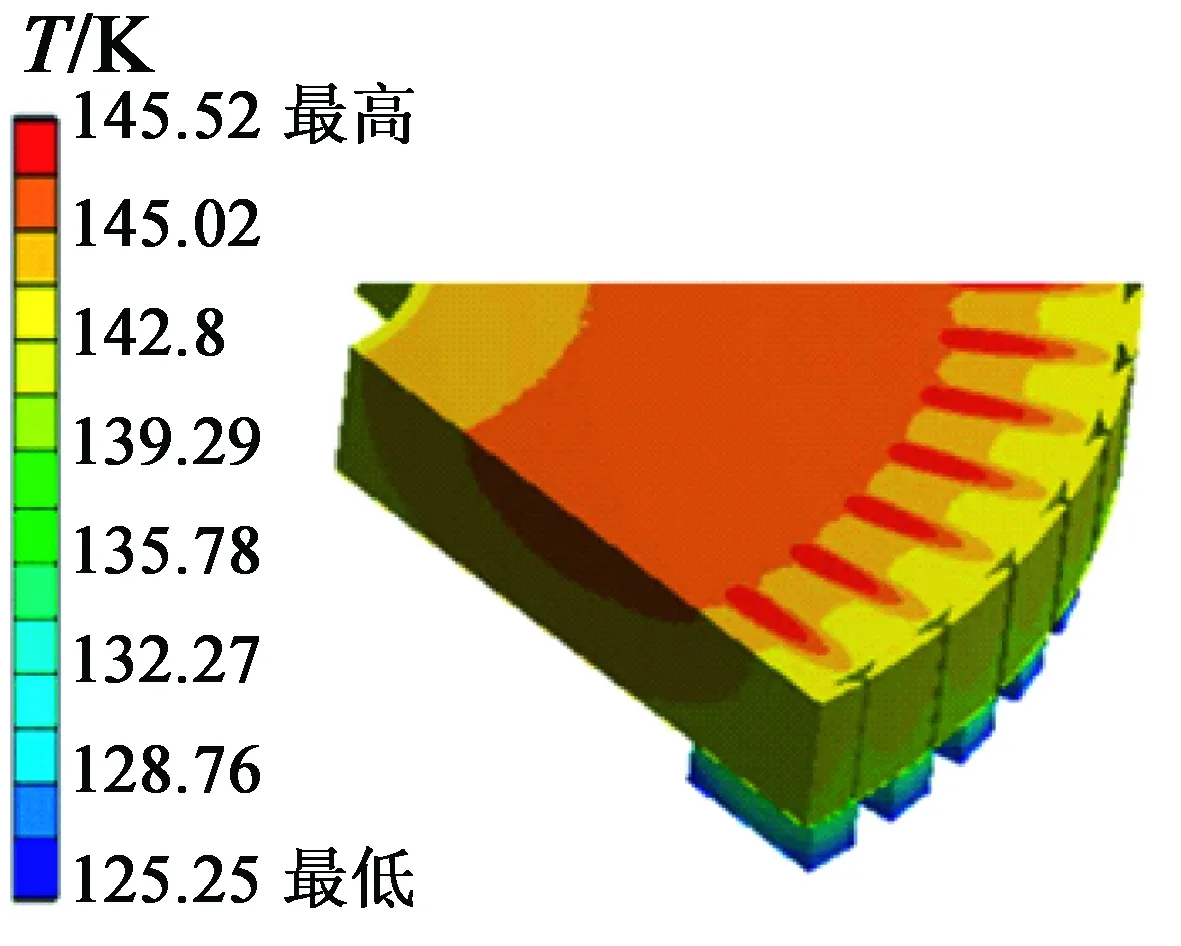
(a) 電機Ⅰ
多目標優化的最終計算結果以及有限元計算次數、計算時間等數據如表3與表4 所示。
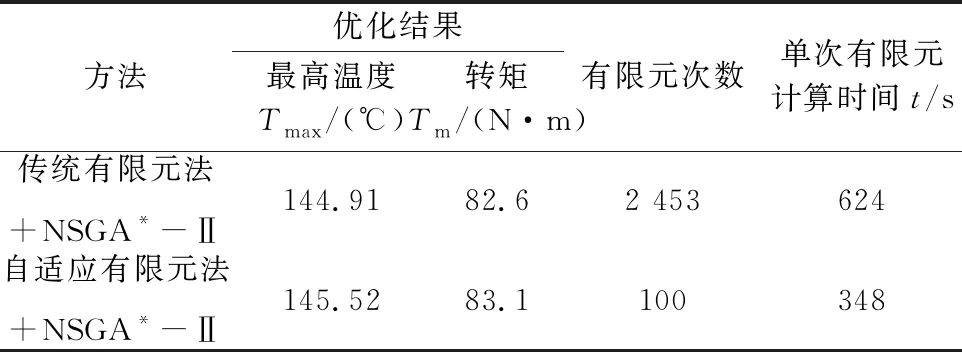
表3 電機I的優化結果比較

表4 電機II的優化結果比較
結果顯示,采用本文的基于自適應有限元法的多目標優化方法,優化結果與基于傳統有限元的多目標優化相比較為準確,能夠在保證結果準確性的前提下,有效地減少優化時間。
3 結 語
本文研究了一種優化永磁電機性能的方法。提出了一種自適應雙層網格有限元方法,通過分離設計區域,避免優化迭代時的整體網格重構。針對影響電機輸出轉矩及溫度的參數變量,即磁鋼厚度、電機軸向長度以及電機內外徑等參數,建立基于移動最小二乘法的響應面模型,與有限元模擬結果對比驗證該模型的可靠性。針對永磁同步電機和徑向磁通調制電機的多目標優化問題,以轉矩與溫度作為目標函數,實施電機結構優化。通過與傳統有限元方法的比較,驗證了準確性與可行性,以及應用該方法可以減少優化過程的計算量。

