指數有界雙連續n階α 次積分C半群的生成定理

周裕然， 趙華新， 周 陽

（延安大學 數學與計算機科學學院，陜西延安 716000）

算子半群的生成理論是算子半群的重要內容之一，許多學者對此作了大量的研究工作. 在文獻［1］中常勝偉和趙華新研究了局部有界雙連續n 次積分C 半群的生成元及其性質. 文獻［2］中張明翠給出了n 階α 次積分C 半群的概念、預解集以及次生成元等，并研究了相關問題. 文獻［3］中常勝偉等討論了指數有界雙連續n 次積分C 半群及其性質. 文獻［4］中趙丹丹討論了雙參數n 階α 次積分C 半群的概念、預解集、逼近以及生成元等. 在文獻［5］中洪偉和喬俊討論了有界線性算子廣義譜的譜映照定理. 文獻［6］中薛雙等討論了雙參數有界算子C 群的生成定理及相關性質. 文獻［7］中李玉霞等討論了指數有界雙連續α 次積分C 半群的擾動等相關定理. 文獻［8］中楊雯雯等研究了α 次積分C 半群的譜映照定理. 文獻［9-10］中秦喜梅和葛國菊研究了指數有界的雙連續n 次積分C 半群及其生成定理及譜映照定理. 文獻［11］中李紀闊討論了n 次積分C 半群的逼近定理和譜映照定理. 文獻［12］中胡敏等介紹了n 次積分C 半群的表示定理. 文獻［13-15］討論了指數有界C 半群的逼近問題.

1 預備知識

在本文中，X為無限維的復Banach空間，B（X）是X 上有界線性算子全體所成的Banach代數；D（A）為線性算子A 的定義域，設n ∈N，α ≥0.

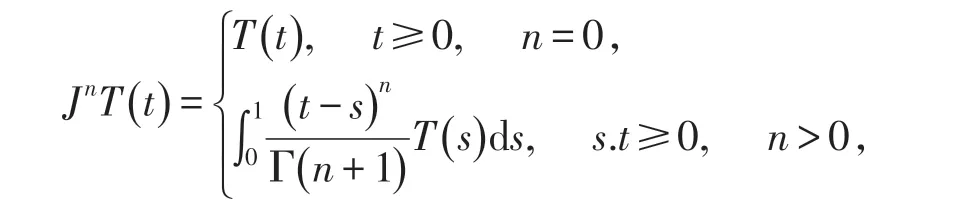
T=0 當且僅當存在n ≥0 使JnT（ t ）=0，t ≥0.

2 基本概念和引理

也即

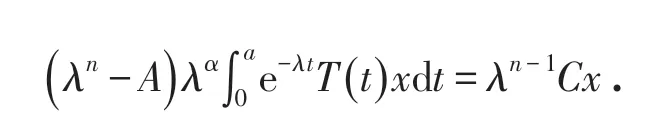
如果x ∈D（ A），可得

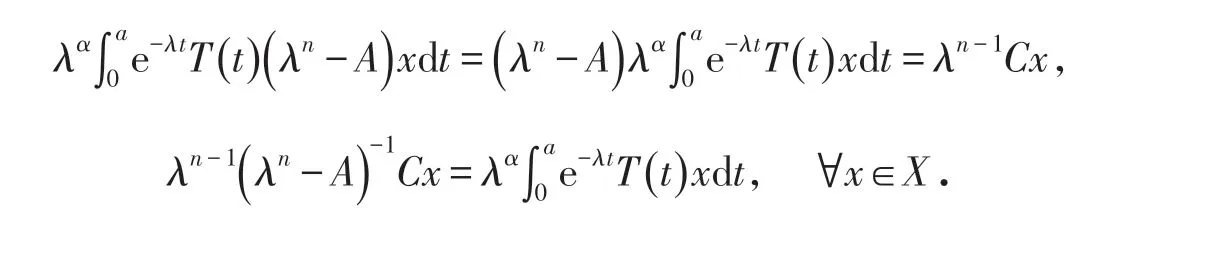
故

定理得證.