方肋微通道內流動沸騰的氣泡動態與傳熱特性分析

申宇，潘振海，吳慧英

（上海交通大學機械與動力工程學院，上海200240）

隨著近年來微電子技術和MEMS工藝在諸多工業領域的飛速發展，電子器件在尺寸縮小的同時，功耗卻不斷攀升。這導致電子設備表面的熱通量激增，嚴重影響系統性能甚至直接燒毀電子器件[1]。帶肋微通道熱沉的流動沸騰換熱在高熱通量芯片熱控制方面具有顯著優勢，得到了廣泛關注[2-10]：與常規通道不同，帶肋微通道的換熱比表面積大，結構緊湊，便于封裝；流動沸騰利用液體相變潛熱，換熱效率高，并能維持較好的壁面均溫性。此外，相較于平滑微通道，其內部的微肋結構還具有強化流體擾動和增加氣化核心的雙重功效，進一步增強對流換熱性能并降低沸騰起始溫度。

國內外諸多學者對帶肋微通道內獨特的氣液兩相流動和相變傳熱機制展開了研究。Lie等[6]通過實驗對比了制冷劑FC-72在帶肋微通道內兩相流和單相流的換熱效果，發現兩相流動的換熱系數遠大于單相流。Krishnamurthy和Peles[7]進行了并排帶肋微通道內的流動沸騰實驗，在通道內沿流動方向分別觀察到泡狀流、泡狀-彈狀混合流、環狀流等不同流型，并且發現帶肋微通道的流動沸騰換熱效率明顯高于光滑微通道。Guo 等[8]分別研究了光滑表面和柱狀微結構換熱面的流動-噴射復合式強化沸騰換熱。結果表明得益于柱間的微對流運動，相比光滑表面，相同工況下柱狀微結構的臨界熱通量（CHF）更高，沸騰穩定性得到提升。Qu 等[10]研究了進口流體過冷度對微通道內流動沸騰的影響，發現當過冷度增大，低含氣率區域的壁面傳熱系數會提高，但是在高含氣率區域傳熱變化不明顯。為了深入理解流動沸騰換熱的諸多物理機制，學者們[11-19]采用數值模擬的方法對該過程進行研究。楊朝初等[11]模擬了微氣泡的生長過程，發現氣泡一旦成核后會迅速吸熱膨脹，并在氣泡與通道壁面之間形成薄液膜。彈狀流是微通道內非常重要的兩相流型，具有良好的傳熱傳質特性[12]。Magnini等[13]基于Hertz-Knudsen 理論和高度函數法構建了高精度的氣液相變模型，對微圓管內彈狀流氣泡的流動沸騰過程進行模擬。結果表明微通道內兩相流的壁面傳熱系數比相同條件的單相流高出30%，并發現薄液膜的蒸發導熱是壁面傳熱強化的主要原因。徐進良等[14]模擬了高熱通量下微圓管內觸發種子氣泡的沸騰傳熱，并分析了不同氣泡觸發頻率對壁面冷卻的影響。從以上文獻可以看出，帶肋微通道具有良好的沸騰換熱性能，但是對流動沸騰過程中所涉及的氣泡運動規律以及肋表面的換熱特性還需進一步研究。

因此本文采用數值模擬的方法，構建氣-液流動和相變模型，對微通道內氣泡繞流加熱方肋這一基本的流動沸騰問題進行研究。以氣泡行為、流場演變以及方肋各表面的傳熱特性變化作為主要研究對象，通過分析初始氣泡體積及入口雷諾數Re 等不同參數的影響，探究帶肋微通道內沸騰氣-液兩相流動及相變傳熱傳質的規律，進而為實驗研究提供指導。

1 模型建立

1.1 物理模型

本文構造一個二維微通道物理模型，如圖1所示。微通道長度L=4mm，寬度D=0.2mm，通道壁面絕熱。邊長B=0.08mm 的方柱設置在通道正中心，方柱壁面為恒定熱通量q=5×104W/m2加熱。各壁面均為無滑移速度條件。微通道入口通入飽和R113制冷劑（Tsat=323.15K），其標準大氣壓下各相物性參數見表1。入口設置充分發展速度條件，出口為標準大氣壓出口條件，并在距離入口0.5mm，靠近通道上壁面的位置初始化一個氣泡。

以D為特征長度，定義入口雷諾數Re[式(1)]。

式中，u為入口平均速度；μl為液體動力黏度。定義局部傳熱系數hx[式(2)]。

圖1 幾何模型和邊界條件

表1 一個標準大氣壓下R113飽和狀態的物性參數

式中，Tw,x為方柱表面局部壁溫。

定義局部努賽爾數Nux[式(3)]。

式中，λl為液相導熱率。

1.2 網格劃分

本文采用ICEM 軟件劃分網格，部分計算區域網格如圖2所示。為了保證計算域內氣液兩相流動與沸騰傳熱特性的準確性，對微通道壁面以及加熱方柱周圍進行了網格加密處理，以確保對薄液膜的刻畫。為了驗證網格的無關性，在此基礎上將原有網格數量提高4倍，方柱換熱系數結果與原網格算例相比差異小于1.5%，因此可認為結果是網格無關解。

1.3 控制方程和算法設置

本研究中的數值模型基于如下假設：

（1）氣液相變溫度恒定為一個標準大氣壓下的飽和溫度；

（2）氣相和液相的熱物性均設置為該飽和溫度下的常值；

（3）不考慮液體黏性加熱；

（4）忽略重力作用。

以上假設的根據是：①微通道內壓降小于5kPa，其對應的液體相變溫度變化小于5%[21]；②最大過熱度低于13K，其對應的氣相和液相的熱物性變化均小于5%[21]；③最大Re 下，黏性耗散對流體的加熱僅為壁面加熱的0.1%[22]；④通道封閉數Co大于5[Co=(σ/gΔρD2)1/2]，重力作用被抑制[23]。

本文使用的流體體積函數（VOF）模型是一種在固定歐拉網格下追蹤氣液交界面的方法。氣相和液相用網格體積分數a 來表示：a=1 為氣相，a=0為液相。氣液界面處0＜a＜1，物性為各相物性體積分數的加權平均值。氣相及液相的質量方程如式(4)、式(5)所示，氣液兩相共用的動量、能量守恒方程如式(6)、式(7)所示。

式(6)中的Fs表示作用于氣液界面的表面張力，通過連續界面力（continuum surface force，CSF）模型將表面力轉化為體積力[式(8)]。

式(7)中的能量源項Sh基于Pan 等[18]提出的“飽和界面體積”相變模型，該模型中認為蒸發過程中氣液界面處維持在飽和溫度，因此計算可以不依賴于經驗系數，其表達式為式(9)。

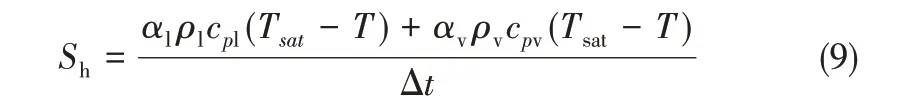
對應的式(4)、式(5)的質量源項表達式為式(10)。

本文使用基于有限體積法的Ansys Fluent 18.0離散型非穩態求解器，流動模型為層流模型。流場采用PISO（pressure implicit splitting of operator）算法求解耦合的壓力-速度方程，對時間項采用隱式格式離散。標量梯度的求解采用“基于節點的格林-高斯”法（Green-Gauss node-based method），采用VOF方法中的“結構重構”方法（geo-reconstruct）追蹤氣液界面。壓力插值采用PRESTO 算法（pressure staggering option），動量和能量方程的對流項均采用三階迎風格式進行離散。為了避免數值振蕩，通過設置CFL 條件實現對時間步長的控制，Courant 數設置為0.05，模擬過程中最大的時間步長為10-7s。質量、動量和能量方程的殘差分別控制在10-6、10-8和10-10以下。

圖2 計算網格劃分

1.4 模型可靠性驗證

為驗證計算模型的精確性和可靠性，本文首先用R113工質對經典的一維Stefan相變問題[24]進行模擬。圖3 給出了氣液界面位置隨時間的變化曲線，可以看出，本文的模擬結果與解析解吻合良好。

圖3 相界面位置隨時間變化

其次，Han和Shikazono[25]實驗研究了微通道內彈狀流的薄液膜厚度變化，本文針對液膜厚度與文獻結果進行對比。在Ca=μu/σ=0.0029 時，測量值為10.2μm，模擬值為10.7μm；Ca=0.044 時，測量值為63.2μm，模擬值為66μm，模擬值與實驗值比較接近。

最后，本文模擬了圓管微通道內彈狀氣泡的流動沸騰，并與文獻[13]中基于Hertz-Knudsen 理論的蒸發模型進行對比，結果如圖4、圖5 所示。可以看出本文的氣泡位置和局部傳熱系數均與文獻結果吻合較好，說明本文采用的模型和方法能夠準確模擬微通道內的相變流動問題。

圖4 氣泡前端位置隨時間變化

圖5 壁面傳熱系數沿軸向分布

2 計算結果及分析

2.1 氣泡動態及流場變化

基于上述模型，本文通過改變入口雷諾數（Re=60～360）和氣泡初始大小（d=0.04mm、0.08mm、0.12mm）進行了一系列模擬，以研究流體流速和氣泡體積對方肋微通道內兩相流動和強化傳熱的影響。

圖6 顯示的是初始直徑d=0.08mm 的氣泡在不同Re 下，流過加熱方柱時微通道內速度場、溫度場以及氣泡形狀的演變過程。其中，氣泡的輪廓在速度云圖中用黑線標識，在溫度云圖中用白線標識，帶箭頭的線為流線。

從圖6左側圖片可以看到隨著Re增大，受流體慣性力作用，氣泡變形程度加劇。同時分析速度場和流線圖，Re 為60 和120 時方柱后表面的尾渦區內有兩個對稱的渦旋；而當Re提高到240后，尾渦區內的渦旋開始周期性地脫落，增強了下游流體的擾動。當氣泡從方柱與壁面的狹縫穿過時，氣液界面掃掠方柱上表面的過熱液體，形成一層薄液膜，擠壓熱邊界層。對比氣泡進出方柱前后，尾渦區的流場和溫度場發生了明顯改變。

圖7 分別是四種Re 下，氣泡的當量直徑deq隨氣泡質心軸向位置xc變化的曲線。其中，氣泡的當量直徑deq定義為同等體積下球形氣泡的直徑；氣泡質心的軸向位置xc可用式(11)計算。

式中，N為計算域的網格數，xi是第i個網格的軸向坐標，ai和Vi分別為該網格的氣相體積分數與網格體積。

圖6 氣泡在4種不同Re下，通過加熱方柱過程中三個位置的絕對速度及溫度云圖

圖7 不同Re下氣泡當量直徑deq隨質心xc位置的變化

從圖7可以看出，當氣泡到達方柱中心時（xc=2mm），氣泡體積開始陡增，說明此時相變蒸發已經開始。從曲線斜率的變化可以看出，受過熱液體分布的影響，氣泡在方柱和尾渦區域（xc=2～2.5mm） 體積迅速增長，而到通道下游（xc＞2.5mm）體積增長則不明顯。此外，氣泡在低Re條件下的增長速度要遠遠大于高Re 的情況，尤其是在尾渦區內。出現該現象的原因主要有兩點：一是高Re 下，氣泡流速快，在過熱區停留時間短，蒸發吸熱過程不充分；二是在高Re 下，流場以渦旋脫落的方式將尾渦區過熱液體帶向通道下游，對冷熱液體進行混合，降低了尾渦區液體的過熱度，從而抑制了該區域的相變蒸發。

2.2 換熱效果分析

2.2.1 入口雷諾數Re對方柱傳熱的影響

圖8對比了4種Re下，方柱四個加熱面平均傳熱強化率隨時間的變化。其中，平均傳熱強化率定義為(htp-hsp)/hsp，反映了兩相流下表面平均傳熱系數htp與相同條件下單相流hsp的相對大小。定義量綱為1 時間τ=t/(B/u)，當氣泡前端靠近方柱時τ 設定為0 時刻。從圖中可以看出，當氣泡穿過方柱時，方柱4個表面的傳熱均受到不同程度影響。其中上表面的傳熱強化最為顯著：在Re=60下，最大的換熱系數超過單相流的4.5 倍。這是因為當氣泡穿過方柱時，氣泡在表面張力的作用下擠壓周圍液體，在方柱的表面和氣泡界面之間形成一層薄液膜（圖4）。此時薄液膜內部流動緩慢，薄液膜的蒸發導熱成為了主要換熱方式，其熱阻較小，強化傳熱顯著[15]。而隨著Re 增大，流體慣性力開始占據主導，液膜厚度變厚，導熱熱阻增大，導致強化傳熱效果迅速下降。方柱前表面和后表面也形成部分液膜，因此具有類似變化規律。而對于方柱下表面，雖然未與氣泡直接形成薄液膜，但由于氣泡堵塞上通道而使下通道的液體流動加快，增強了下表面的對流傳熱強度。

圖8 方柱各表面兩相流傳熱強化率隨量綱為1時間τ的變化

進一步對方柱4個表面的傳熱強化率做積分平均，圖9(a)比較了4種Re下方柱整體傳熱強化率隨時間的變化；對氣泡前端靠近方柱直到氣泡尾端離開方柱這段時間進行積分平均，圖9(b)統計了方柱的時均-整體傳熱強化率與Re的關系。從這兩個圖都可以看出，在氣泡流經方柱的過程中，Re越小，氣泡流動沸騰對方柱整體傳熱強化效果越明顯。

圖9 氣泡流經方柱過程方柱整體換熱強化率的變化

2.2.2 氣泡初始直徑對方柱傳熱的影響

圖10 比較了Re=120 下3 種量綱為1 初始直徑的氣泡（= deq/D），其質心位置xc恰好位于方柱中心位置（即xc=4mm）時氣泡的形狀、方柱壁面過熱度以及對應的局部努賽爾數Nux的分布情況。

圖10 不同初始體積的氣泡穿過方柱的對比

3 結論

本文基于VOF 方法，采用“飽和界面”相變模型，以R113 為工質對帶肋微通道內氣泡流動沸騰進行了二維數值模擬，分析了氣泡體積和入口雷諾數Re 對氣泡增長速率、液膜厚度和方柱表面傳熱等重要傳熱傳質參數的影響規律。得到如下結論。

（1）氣泡穿過方柱時，在氣泡界面和方柱表面之間形成一層薄液膜，擠壓溫度邊界層；氣泡對尾渦區的流動結構存在擾動作用。

（2）氣泡的蒸發相變主要發生在方柱和尾渦區內，且Re越小，氣泡的體積增長越快。

（3）薄液膜的蒸發導熱是傳熱強化的主導機制，氣泡的流動沸騰對方柱表面換熱有明顯的強化作用；對于相同體積的氣泡，隨著Re 增加，液膜厚度逐漸變厚，強化傳熱作用迅速減弱。

（4）對于相同Re，氣泡體積越大，所形成的薄液膜區覆蓋面積就越大，液膜蒸發帶來的強化換熱也越顯著；而小氣泡的兩相流換熱效果同單相流相比并無明顯差異。

符號說明

B—— 方柱邊長，mm

Co—— 通道封閉數，(σ/gΔρD2)1/2

Ca—— 毛細數，μu/σ

cp—— 比定壓熱容，J/(kg·K)

D—— 通道寬度，mm

d—— 氣泡直徑，mm

Fs—— 體積表面張力，N/m3

g—— 重力加速度，m/s2

hfg—— 氣化潛熱，kJ/kg

hx—— 對流換熱系數，W/(m2·K)

L—— 通道長度，mm

Nux—— 局部努賽爾數

n—— 單位法向量

p—— 壓強，Pa

q—— 熱通量，W/m2

Re—— 入口雷諾數，Re=ρluD/μl

Sm—— 質量源項，kg/(m3·s)

Sh—— 能量源項，W/m3

t—— 時間，s

U—— 速度矢量，m/s

u—— 軸向速度，m/s

a—— 體積分數

λ—— 熱導率，W/(m·K)

μ—— 動力黏度，Pa·s

ρ—— 密度，kg/m3

σ—— 表面張力系數，N/m

τ—— 量綱為1時間，tu/B

x—— 軸向坐標，mm

下角標

c—— 質心

eq—— 當量

l—— 液相

sat—— 飽和狀態

sp—— 單相流

tp—— 兩相流

w—— 壁面

v—— 氣相