從《一元二次不等式的解法》談數學課堂的生成性教學
劉曉偉
(江蘇省南京市聾人高級中學 210006)
一、教學背景
1.課例介紹
本節課是蘇教版必修5和第三章《不等式》中的第二節的內容.本節課是作者在校教研組內開設的一節公開課,并且參加了2017年的一師一優課的曬課活動,并且得了一等獎.
2.學情分析
本課之前,學生已經具備了二次函數、解一元二次不等式等相關知識,這些知識的掌握是學習本節課的基礎條件.也應對于畫二次函數的圖象,以及根據圖象寫對應x或y的范圍等相關知識點有一定的基礎.但是,對于聾生相對與聽力健全的學生,雖然已經進入高一,但是邏輯思維能力、探究問題的能力仍舊非常欠缺.
3.教學方法
以建構主義理論為指導,根據內容特點,結合學情,通過設置問題,開展教學活動,使學生經歷探究過程,在師生間展開分析、交流、溝通、質疑、思辨,總結等活動,在活動中,創設生成性教學,幫助和指導學生,促進生成性學習.
二、課堂教學實錄片段
1.以舊知引出新知,激發學生思維
問1:如何解一元二次不等式x2-x-6>0.
我們利用學習過的解一元一次不等式的方法可以解決嗎?
問2:把x2-x-6>0改寫為x2-x-6=0,變成了什么?
生1:變成了一元二次方程,解為x1=3,x2=-2.
問3: 把x2-x-6>0改寫為y=x2-x-6,變成了什么?
生2:變成了二次函數,我們可以畫出它的圖象.
問4:我們可以利用這兩個工具來解一元二次不等式嗎?
設計意圖:由學生已經掌握的知識嘗試來解決新的知識,是數學中最為常用的方法,通過問題的設計來不斷地引出新的問題的解題思路.
2.數學建構,探究新知
作二次函數y=x2-x-6的圖象,回答如下問題:
(1)圖象與x軸交點的坐標為____.
(2)該坐標與方程x2-x-6=0的解有什么關系:____.
(3)當x取____時,y=0?
當x取____時,y>0?
當x取____時,y<0?
(4)由圖象寫出解集:
不等式x2-x-6>0的解集為____.
不等式x2-x-6<0的解集為____.
總結歸納:
(1)拋物線與x軸的交點的____就是對應的一元二次方程的____.
(2)不等式的x2-x-6>0解集為____.
(3)不等式x2-x-6<0的解集為____.
設計意圖:以一個具體的例子來分析二次函數、一元二次方程以及一元二次不等式的具體關系,利用數形結合以及師生互動的方法,讓學生理解解一元二次不等式的方法,讓學生體會解法的獲取過程,從而提高學生獲取知識的能力.
3.例題解析,鞏固新知
例1解一元二次不等式:x2-x-6>0.
問:從以上的分析過程,你能總結出解一元二次不等式有哪些步驟嗎?
步驟:
(1)解:解對應的一元二次方程.
(2)畫:畫出對應的二次函數的圖象.
(3)寫:結合圖象寫出一元二次不等式的解集.
給出標準格式:
Δ>0,方程x2-x-6=0的解為x1=3,x2=-2.
根據y=x2-x-6的圖象,可得x2-x-6>0的解集為{x|x>3或x<-2}
4.小組合作,深化新知
以小組合作的形式完成表格再匯報交流.(a>0)
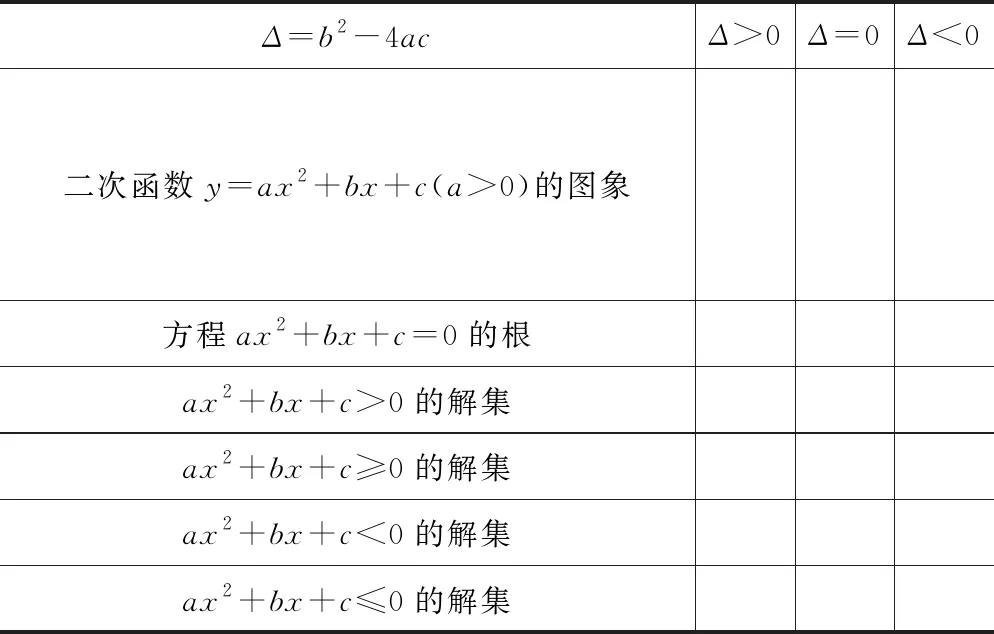
Δ=b2-4acΔ>0Δ=0Δ<0二次函數y=ax2+bx+c(a>0)的圖象方程ax2+bx+c=0的根ax2+bx+c>0的解集ax2+bx+c≥0的解集ax2+bx+c<0的解集ax2+bx+c≤0的解集
5.課堂總結,升華精髓
問:哪位同學可以總結一下本節課的收獲?
生:學習到了解一元二次不等式的方法,以及二次函數、一元二次方程和一元二次不等式的關系.
三、課后反思
1.格式化語言的使用幫助聾生提高思維能力
聾生的思維能力較聽力健全的學生有著很大的差距,其思維中存在的機械性記憶為學習基礎,思維過程跳躍而缺乏邏輯線索,不在意因果關系而盲目堅持自己的偶得觀點等特點;體現在數學解題過程中就是解題過程不規范,書寫不夠完整,這也從側面證明了聾生在解決問題的時候缺乏一定的邏輯思維能力,所以對于一些重點例題的解題過程,給予一種相對固定的解題格式,并通過反復訓練來幫助聾生發展邏輯思維能力.這對于聾生理解問題、解決問題能力的提高起到了很大作用.在進行了長時間的格式化解題的訓練之后,聾生數學題的書寫更符合規范和要求,思維混亂的狀況會大幅度改變.
2.重視學生的參與程度,提高學習能力
聾校高中數學教學普遍存在節奏快、容量大、教師講得多、學生理解得少等現象.教師不自覺地把學生當成知識的容器、完成教學進度的工具.其實,教師應該放慢腳步,這樣做是為了把發現、探究、體驗等機會留給學生,讓學生有機會反思自我,展現自我,有足夠的時間去消化積累,提升學科素養,積累內在力量,完成“數學知識忘記后沉淀下來的東西”,實現真正的數學思維能力的提高.本節課中,就一直以問題為主線,把本節課要學習的內容,通過一系列的學生活動,展現出來,同時找到了解決問題的方法,解決了重點和難點內容.
本節課的教學遵循學生獲取知識的規律,通過對以往的教育經驗細致思考,分析了解聾生的認知特點,在聾生有別于聽力健全學生的“最近發展區”中設計問題.以減少聾生“跨越臺階”的難度并通過適度的加問、必要的追問,充分利用現代教育技術,結合學生小組討論、合作探索,讓學生循序漸進地掌握了一元二次不等式的解法的相關知識,學生從已經獲得的關于二次函數、一元二次方程入手,利用數形結合的方法,先觀察它們之間的關系,再小組間合作,由聾生親手總結出它們之間的具體關系,最后形成解決一元二次不等式的解決方法.整個教學過程都是以學生為主體,教師加以輔助,努力讓學生自己生成解決的方法,突出了學生的主體地位,同時顯示了知識的生成過程,提高了學生的思維能力.

