舉升平臺雙剪刀叉結構的推力與有限元分析
□ 周 旭 □王 娟
1.索恩格汽車部件(中國)有限公司 長沙 4101292.中國電子科技集團第四十八研究所 長沙 410111
1 舉升平臺概述
剪刀叉舉升平臺分為固定式、拖動式、車載式三種,雖然形式各有不同,但是舉升動作都是由驅動系統、電動控制系統、剪刀叉結構、工作平臺四部分共同完成。
液壓驅動系統運行平穩,可以通過油缸活塞桿的伸縮來推動剪刀叉結構實現展開與折疊,所以剪刀叉舉升平臺選用液壓驅動系統最為常見。
剪刀叉結構在舉升過程中能夠保持較好的穩定性,如果高空作業工作范圍大,需要較強的承載能力,那么可以設計寬大的工作平臺,選用高強度鋼作為剪刀叉結構材質,并且通過結構優化,達到質量小、承載能力強的效果。
目前,剪刀叉舉升平臺在物流、設備維護、航空裝卸等領域應用廣泛。對于剪刀叉結構,可以根據受載大小選擇型材,小載荷時可以選用長條形板,大載荷時可以選用方管。
孫光旭等[1]基于液壓和機械系統的耦合作用,結合動力學仿真分析,得出舉升平臺剪刀叉結構的驅動力。海闖等[2]對三剪刀叉結構的鉸點及油缸受力進行了理論計算,并進行了結構仿真,得到初始狀態和完全升起狀態為最危險工況。趙曉[3]對剪刀叉舉升平臺進行了整體有限元分析,并基于多目標遺傳算法優化了油缸推力和整體應力。張威等[4]介紹了油缸處于不同位置時剪刀叉結構輸入力的統一計算式,但在某些情況下計算式計算結果與仿真結果存在一定偏差。李敏[5]通過仿真分析得出了舉升平臺剪刀叉結構的油缸推力。李鄂民等[6]應用虛功原理得出剪刀叉結構油缸推力與機構載荷的關系式。Sun Leibo等[7]針對不同結構形式計算出剪刀叉舉升平臺的最大舉升力。孫毅[8]分析了剪刀叉結構三種布置方式的油缸推力,并進行了強度研究。在目前已有的研究中,舉升平臺剪刀叉結構的推力大部分基于單一仿真模型或單一理論計算得到,缺乏準確性驗證,且少有對雙剪刀叉結構的推力進行計算。另一方面,對舉升平臺剪刀叉結構進行有限元分析,一般只分析靜強度,而沒有對穩定性進行校核。針對上述現有研究的不足,筆者對舉升平臺雙剪刀叉結構的油缸推力進行理論推導,對結構的強度進行有限元分析,并進行穩定性校核。
2 推力理論推導
油缸推力是確定剪刀叉舉升平臺液壓驅動系統參數的首要條件,在進行舉升平臺結構設計時應盡早獲得,以便對液壓驅動系統進行選型。舉升平臺雙剪刀叉結構如圖1所示,由油缸驅動,共有十個轉動副、一個油缸移動副、兩個支點移動副,J1、J2、J3、J4為底層剪刀叉的四個鉸點。設剪刀叉長為l,剪刀叉升角為α,油缸升角為γ。油缸的兩個支點I(Ix,Iy)、J(Jx,Jy)位于兩根剪刀叉的外伸梁上,上外伸梁長度為c,上外伸梁與剪刀叉的夾角為θ,上外伸梁固定點H與剪刀叉中心的距離為a,下外伸梁長度為d,下外伸梁與剪刀叉的夾角為β,下外伸梁固定點K與剪刀叉中心的距離為b。平臺所受載荷P作用于平臺中心點M(Mx,My),油缸推力為F。將鉸接位置和兩個支點移動副視為理想約束,根據虛功原理[9-10],得到虛功方程:
δWF=0
(1)
F(-δIxcosγ+δIysinγ)+F(δJxcosγ-
δJysinγ)-PδMy=0
(2)
Ix=(l/2-a)cosα+ccos(θ+α)
(3)
Iy=lsinα+(l/2-a)sinα+csin(θ+α)
(4)
Jx=(l/2+b)cosα-dcos(β-α)
(5)
Jy=(l/2-b)sinα-dsin(β-α)
(6)
My=2lsinα
(7)
式中:WF為外力功。

▲圖1 舉升平臺雙剪刀叉結構
由Ix、Iy、Jx、Jy、My對α取微分,得到:
F=2Plcosα/{[-(a+b)sinα-dsin(β-α)+
csin(θ+α)]cosγ+[(l-a+b)cosα+
ccos(θ+α)-dcos(β-α)]sinγ}
(8)
其中,cosγ和sinγ可以根據Ix、Iy、Jx、Jy求得。
由上述理論推導可知,Ix、Iy、Jx、Jy、a、b、c、d、β、θ、l、α、P都會影響油缸推力。在尺寸參數確定的情況下,根據剪刀叉升角α和平臺載荷P,利用式(8)可以快速計算出任意時刻的油缸推力,為液壓驅動系統參數的確定提供依據。
3 動力學仿真驗證
通過實例對式(8)進行動力學仿真驗證,所研究分析的舉升平臺雙剪刀叉結構實例如圖2所示。在ADAMS軟件中根據實際鉸點位置建立仿真模型,如圖3所示。在剪刀叉臂相互連接的鉸點處,以及油缸和剪刀叉臂連接的鉸點處設置轉動副,在油缸和活塞桿間設置移動副。平臺中心所受載荷為P,施加到頂層鉸點A1、A2、B1、B2上,施加給各個點的載荷會隨平臺升高而變化,可根據力平衡和力矩平衡原理求得,在ADAMS軟件中通過函數表達式進行設置。

▲圖2 舉升平臺雙剪刀叉結構實例▲圖3 舉升平臺雙剪刀叉結構仿真模型
通過ADAMS軟件進行仿真,輸出剪刀叉舉升平臺舉升過程中油缸推力與剪刀叉升角的對應關系。將仿真得到的剪刀叉升角代入式(8),得到理論計算結果。將理論計算結果與仿真結果進行對比,繪制油缸推力與剪刀叉升角的關系曲線,如圖4所示。
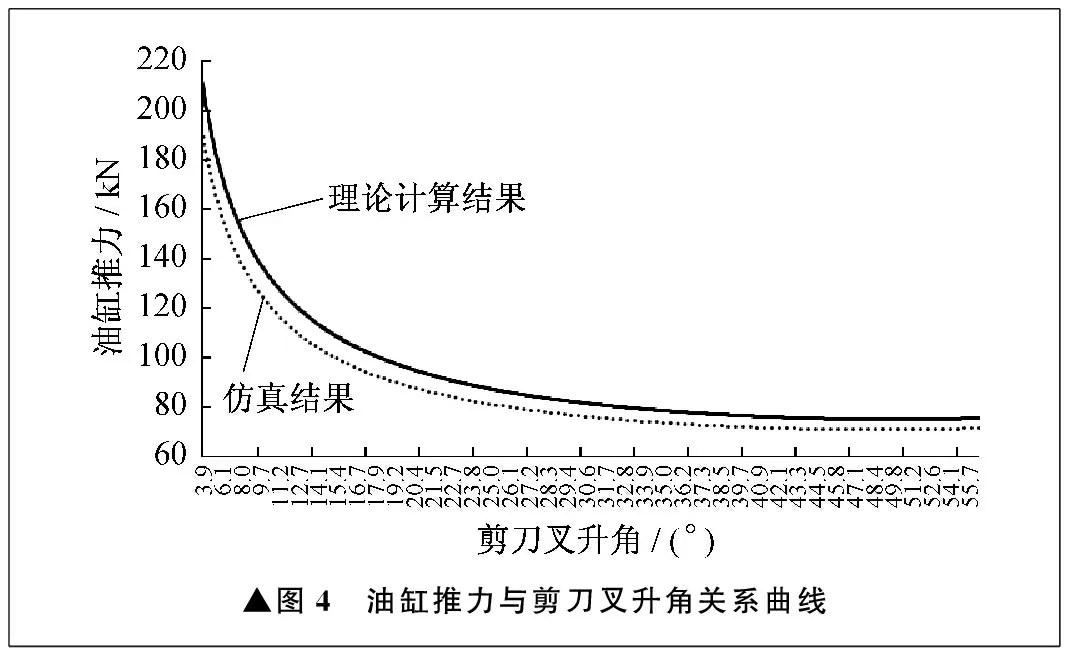
▲圖4 油缸推力與剪刀叉升角關系曲線
由圖4可知,理論計算結果和仿真結果的誤差很小,由此驗證了式(8)的正確性。進一步分析,可以得到如下結論:
(1) 在舉升過程中,隨著剪刀叉升角的增大,油缸推力減小,舉升初始點的油缸推力最大;
(2) 在舉升初始階段,油缸推力隨著剪刀叉升角的增大而急劇減小,應關注此階段的速度沖擊和液壓沖擊;
(3) 在舉升后期,油缸推力趨于平穩,舉升平臺運行也比較平穩。
基于舉升初始點的油缸推力,可以計算出液壓驅動系統的壓強,進而確定液壓驅動系統的參數。如果最大油缸推力過大而產生不良影響,那么可以通過調整油缸位置、剪刀叉長度、剪刀叉升角等來進行改進。
4 有限元分析
進一步應用ADAMS軟件分析得到舉升平臺雙剪刀叉結構各鉸點的鉸點力與剪刀叉升角的關系。限于篇幅,以底層剪刀叉為例,分析得到舉升平臺舉升過程中J1、J2、J3、J4四個鉸點的鉸點力與剪刀叉升角的關系,如圖5所示。舉升初始點底層剪刀叉鉸點力最大,因此分析對應工況下的強度。由于剪刀叉為薄壁細長桿,在大載荷情況下容易產生失穩,因此穩定性也需要進行校核。
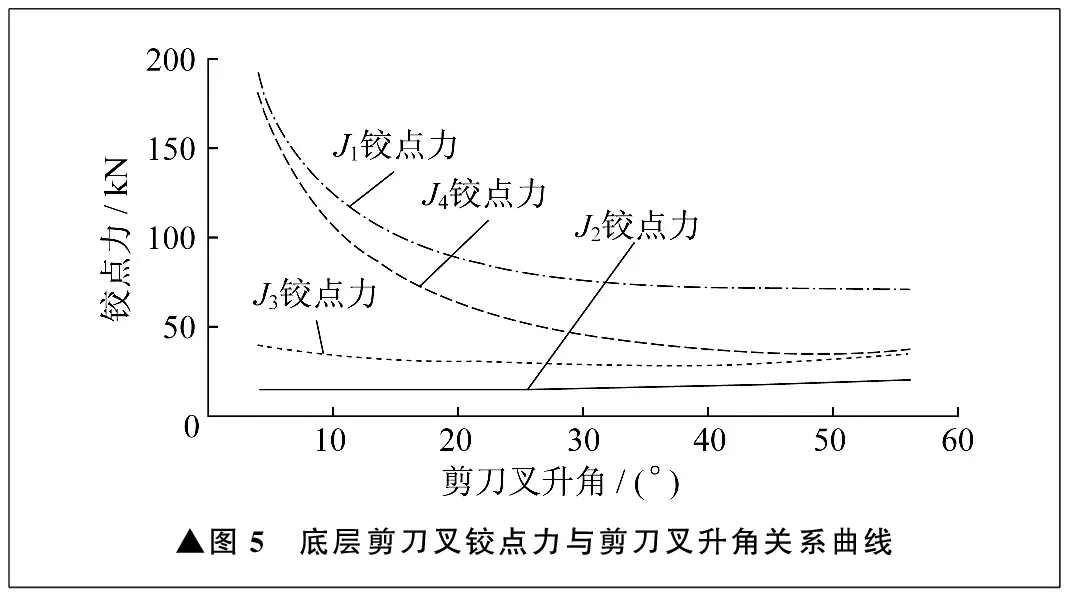
▲圖5 底層剪刀叉鉸點力與剪刀叉升角關系曲線
舉升平臺雙剪刀叉結構由方管、圓管、板等薄壁材料焊接而成,分析時采用面模型劃分殼單元,提高計算效率,同時保證準確性。材料采用Q345鋼,許用應力為235 MPa。在ANSYS Workbench軟件中固定鉸點J2,在其它鉸點處施加仿真得到的鉸點力,得到底層剪刀叉應力云圖,如圖6所示。由圖6可知,最大應力小于許用應力,靜強度滿足要求。屈曲分析結果顯示,一階屈曲因數為4.8,大于2,確認穩定性滿足要求。
5 結束語
筆者運用虛功原理推導了舉升平臺雙剪刀叉結構推力的理論計算式,并通過ADAMS軟件進行仿真,確認仿真結果與理論計算結果誤差很小,由此驗證理論計算式的正確性。應用理論計算式,可以在設計時快速求得剪刀叉舉升平臺的油缸推力。通過ADAMS軟件還得到了雙剪刀叉結構中底層剪刀叉鉸點力與剪刀叉升角的關系,并對底層剪刀叉結構進行了有限元分析,對穩定性進行了校核,確認結構的強度和穩定性滿足要求。

▲圖6 底層剪刀叉應力云圖

