不同參數組合下縱肋頂板細節疲勞開裂時焊趾關鍵測點應力變化分析

吳曉東

(西南交通大學，四川成都 610031)

正交異性鋼橋面板由于其自重輕、極限承載能力大、易于裝配化施工等優點，在國內外公路和鐵路橋梁中得到廣泛的應用。然而，該類結構在有著眾多優點的同時，由于其結構構造復雜，焊縫較多，應力集中問題突出，并且局部承受汽車輪載反復作用，疲勞開裂問題十分普遍。疲勞開裂一旦出現，其修復一般需要中斷交通并且費用高昂，嚴重影響結構的使用性能和運營與服役質量[1]。在正交異性鋼橋面板的眾多疲勞易損部位中，縱肋頂板焊縫開裂所占比例較大，所造成的危害也最嚴重[2]。根據美國土木工程學會疲勞與斷裂分委會的調查結果，80 %～90 %的鋼橋破壞與疲勞有關，疲勞已成為鋼橋結構失效的主要原因之一[3]。為了理清不同結構參數下此焊接處焊趾附近應力下降規律，本文擬建立不同熔透率及不同頂板厚度有限元模型，提取離焊趾5mm處應力，對比不同結構參數下關鍵測點應力隨裂紋擴展過程的變化。

1 試驗介紹

本文擬根據文獻[4]中試驗模型建立相應的有限元模型。試件的頂板的一部分通過高強螺栓將試件固定于試驗工裝上。試件主要結構參數為：頂板厚度為14mm或16mm，U肋腹板厚度8mm，縱肋腹板與頂板夾角為78 °，熔透率取80 %部分熔透和100 %完全熔透兩種。疲勞試驗過程中通過振動疲勞試驗機進行加載，加載面積為100mm×160mm。試件所施加荷載通過離焊趾5mm測點的應力進行控制，本文所施加荷載為100MPa。

2 有限元模型建立及模型驗證

2.1 有限元模型的建立

本文采用通用有限元軟件ANSYS[7]建立試件有限元模型，試件所有結構均采用實體單元Solid45[8]進行模擬，并在裂紋擴展區域對網格劃分進行細化，取距結構中心各6cm焊縫長度作為子模型，利用ANSYS內嵌cint命令實現子模型中裂紋擴展。鋼材彈性模量取2.0×105MPa，泊松比取為0.3。所建立的試件有限元模型及子模型選取如圖1所示。

(a)全局模型

(b)所選子模型圖1 全熔透全局模型及子模型

2.2 模型有效性驗證

由裂紋擴展情況與斷裂力學[5-6]相關理論知識，可以得到裂紋擴展疲勞壽命與裂紋擴展長度之間的關系，通過與文章中所列實測結果對比，可以看出，有限元模型能夠與實測結果較好地吻合，從而證明此有限元模型可以用于后續內容的展開。對比結果如圖2所示。

圖2 有限元模型與實測結果對比

3 計算結果對比

3.1 計算結果提取

有限元模型建立之后，設定裂紋初始尺寸及擴展步長后，應用ANSYS中Cint命令實現裂紋擴展，并從結果文件中提取關注點橫向應力大小和中裂紋擴展深度。為了方便對比，裂紋擴展深度及關注點應力變化均處理為無量綱的百分比形式。現將不同參數下的對比結果列出。

3.2 結算結果對比

相同熔透率不同頂板厚度下關注點應力變化如圖3所示。

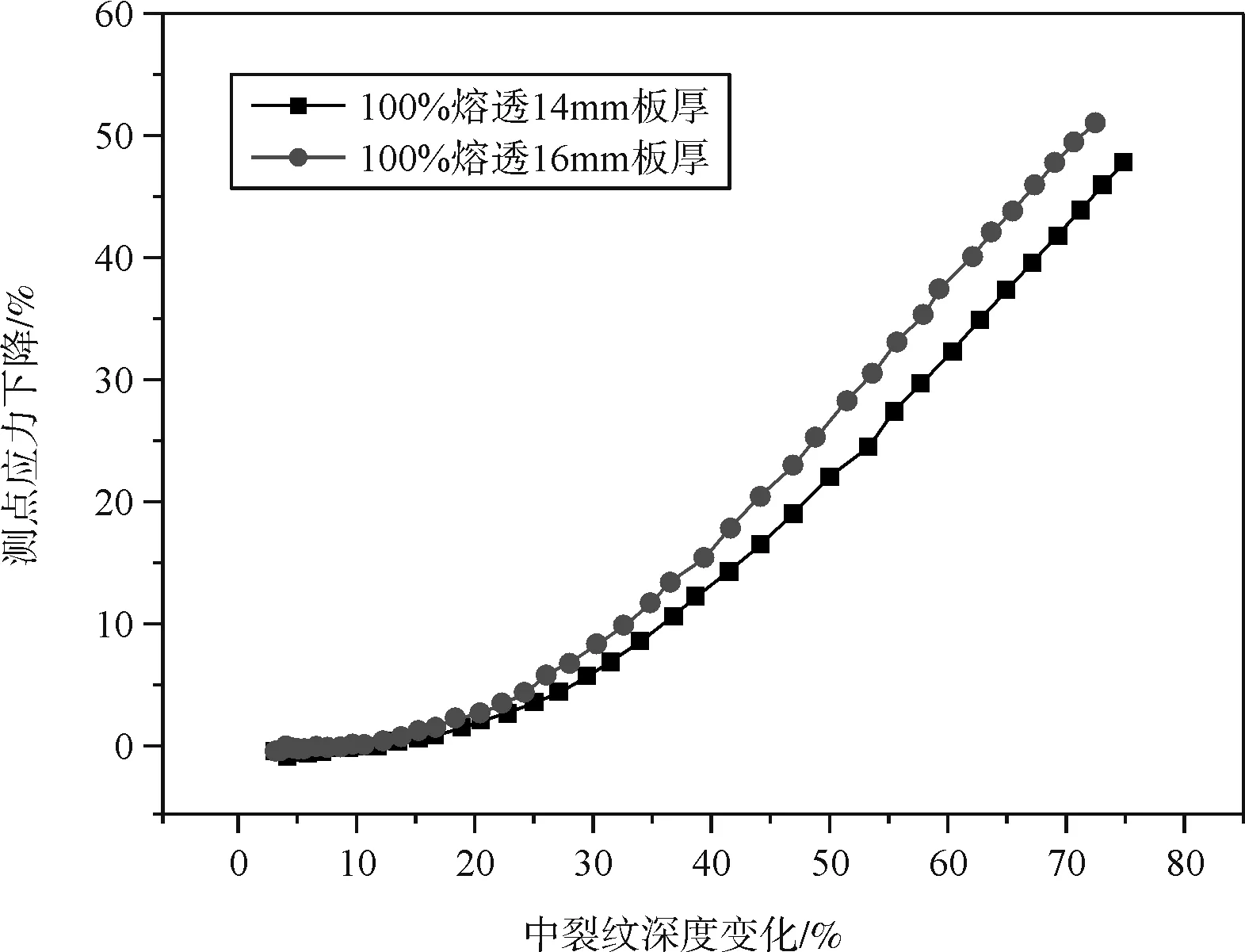
(a)全熔透時不同板厚曲線對比

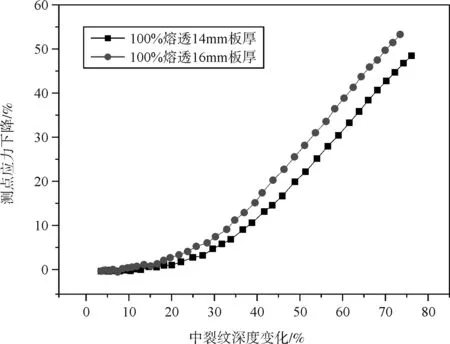
(b)80%熔透時不同板厚曲線對比圖3 相同熔透不同板厚應力變化曲線

通過以上兩圖中的對比可以發現，不管是在哪種熔透率的情況下，當頂板厚度取為14mm時應力下降水平均較相同情況下取16mm時頂板厚度時要快。

兩種板厚下取不同熔透率時關注點應力下降變化如圖4所示。

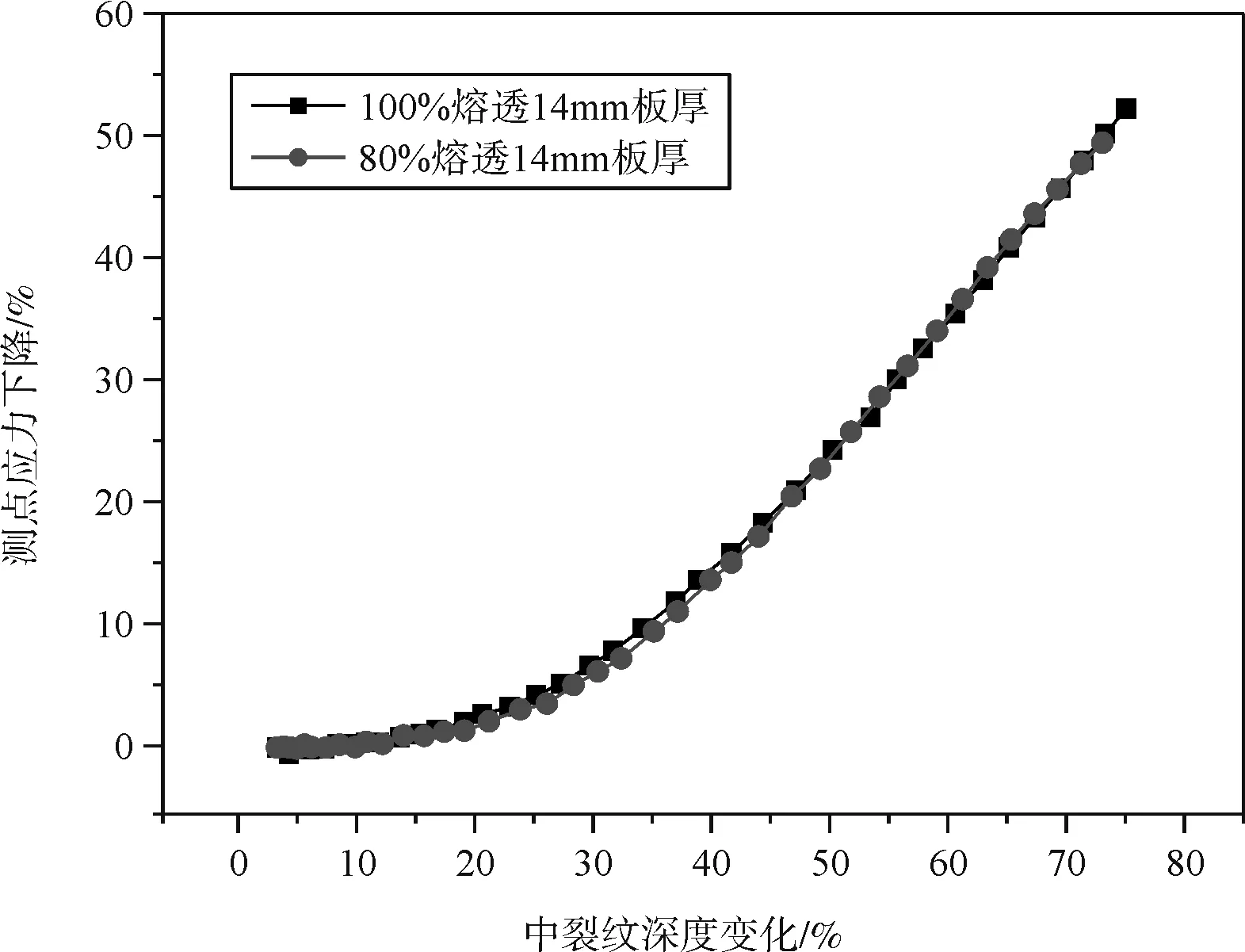
(a)14mm板厚時不同熔透率曲線對比

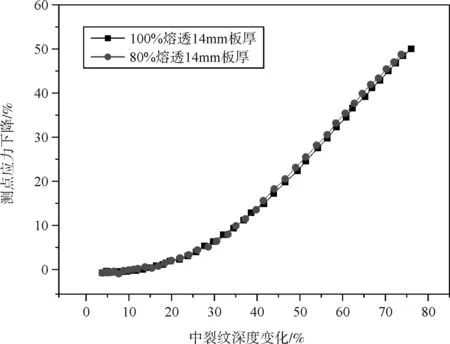
(b)16mm板厚時不同熔透率曲線對比圖4 兩種板厚取不同熔透率應力變化曲線

通過以上兩圖中曲線變化對比可以發現，在取相同的頂板厚度時，不同的熔透率對曲線的變化基本沒有影響，也就是說，熔透率對應力下降隨裂紋擴展深度的變化規律沒有影響。

4 結論

(1)通過驗證，所建有限元模型能夠較為準確地反映實際結構的受力情況，因此可以用于進行后續內容的展開。

(2)通過不同結構參數之間的對比可以發現，當所取結構取相同的熔透率時，不同頂板厚度下，曲線變化呈現出相同的規律，但是變化程度有所不同，在取較大的頂板厚度時關注測點應力下降水平相對較慢；而當取相同的頂板厚度時，不管選用哪種熔透率，曲線變化基本相同，也就是說熔透率對關注測點應力變化隨裂紋長度的變化規律幾乎沒有影響。

(3)通過以上曲線的綜合對比，增加頂板厚度能夠有效增加結構剛度，減緩裂紋的擴展過程。