層狀軟巖隧道穩定性及受力變形特性研究

周 星， 高 杭， 衛亞科， 胡 煒

(1.西南交通大學土木工程學院，四川成都 610031； 2 .中鐵十二局集團有限公司，山西太原 030024； 3.中鐵二院集團有限責任公司，四川成都 610031)

隧道在穿越層狀巖體時，由于巖體傾斜且存在層理、節理等弱結構面，隧道的開挖擾動可能使得圍巖產生局部失穩，圍巖和襯砌結構可能會承受不對稱的偏壓荷載[1-3]。對于層狀軟巖引起的偏壓隧道及其圍壓壓力的計算方法研究一般分為模型試驗和數值模擬兩類。如周曉軍[2]對順層巖體作用于隧道襯砌結構的偏壓載荷進行了模型試驗，得出了地質順層偏壓隧道圍巖壓力的分布特點及其與不同順層傾角之間的變化關系；裴曉彤[4]應用ABAQUS面-面接觸分析對地質偏壓隧道圍巖壓力及襯砌結構內力進行非線性接觸分析與計算；李曉紅等[5]結合共和隧道現場監測和數值模擬相結合的方法對隧道層狀巖體的破壞特征進行了分析；夏彬偉[6]通過數值模擬等手段對深埋隧道層狀巖體的圍巖變形破壞機理進行了研究。以往的數值模擬大多是將層面和基巖分別模擬再定義接觸，將層面視為一種特殊的結構，但這種方法不適用于層厚較薄、分層較多的復雜地質模型[7]。

本文以鄭萬高鐵為工程背景，建立符合圍巖體特征的節理材料模型，并結合現場量測結果，研究層狀軟巖隧道在不同層理面角度下的隧道穩定性及其受力變形特征。

1 工程實例

1.1 隧道概況

在建鄭萬高鐵為設計時速350km/h雙線隧道。某隧道進口里程DK500+200，出口里程DK513+980，全長14 574m。以里程DK508+297隧道截面為研究對象，埋深240m，圍巖巖性為頁巖夾砂巖，多為薄層狀，層厚10～20cm，屬Ⅳ級圍巖，巖層走向與隧道軸線方向一致，傾角大約45°，傾向隧道右側。斷面掌子面圍巖情況見圖1。

圖1 DK508+297掌子面圍巖

1.2 現場監測

根據現場實際情況，選取隧道斷面上幾個典型特征點進行量測，特征點分布如圖2所示。在圖中所示特征點初期支護背面埋設壓力盒，量測圍巖壓力，并量測記錄邊墻、拱腰、拱頂五個特征點的圍巖位移。

圖2 斷面典型特征點布置

2 算例模型

2.1 建立模型

應用ABAQUS軟件，以隧道斷面圖為基礎建立隧道模型，隧道位于模型中心。圍巖和襯砌均采用solid實體單元模擬，襯砌結構與圍巖之間的接觸采用面—面接觸的方式。左右邊界約束水平位移，底邊約束水平和垂直位移。圖3是按深埋隧道建立的計算模型初始豎向應力。

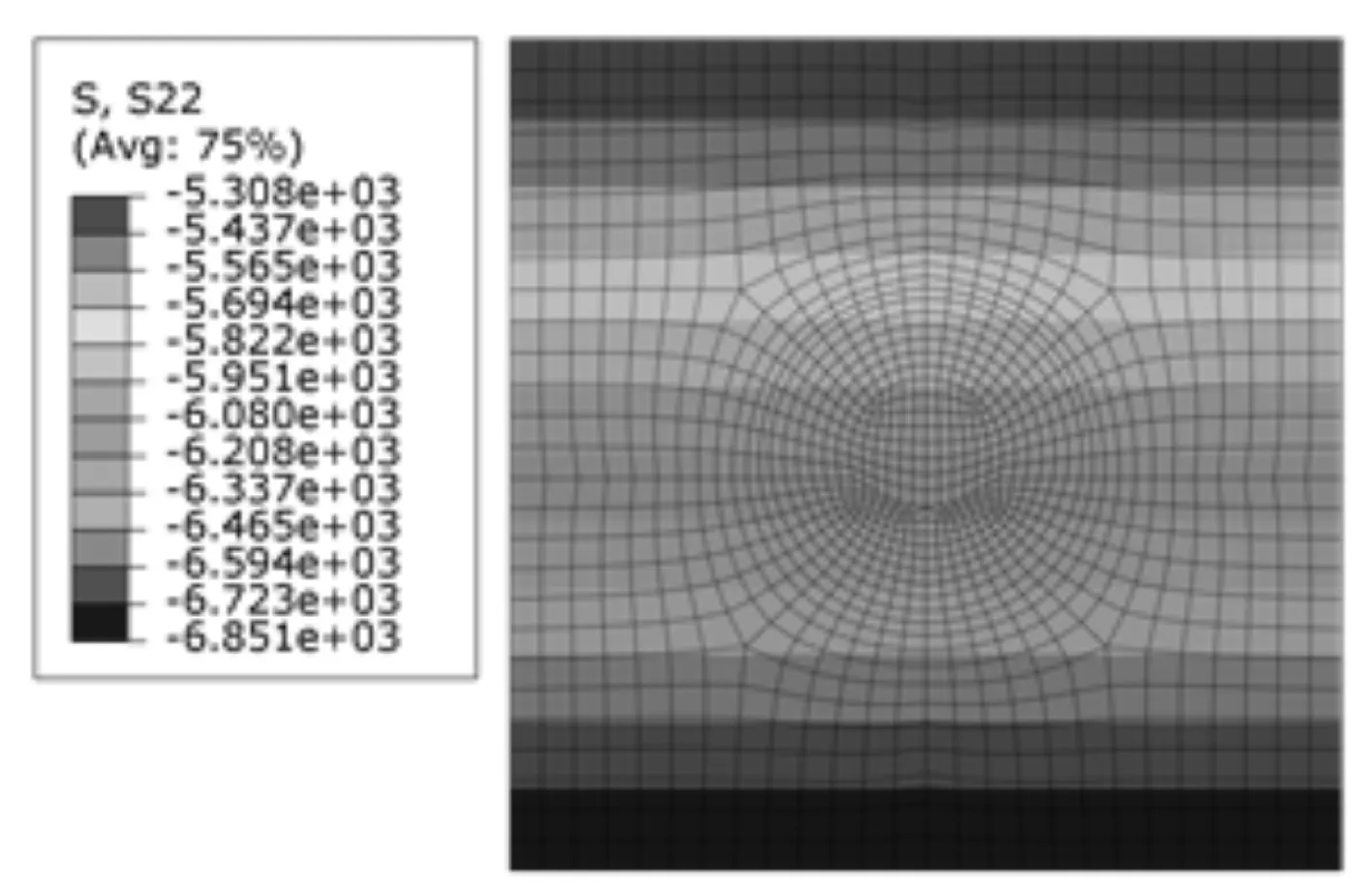
圖3 初始豎向應力場(單位：kPa)

2.2 計算參數

結合隧道現場地勘資料、相關文獻[8]和教程[9、10]，相關計算參數見表1。襯砌采用線彈性模型，而巖體和層理面采用ABAQUS節理材料模型。

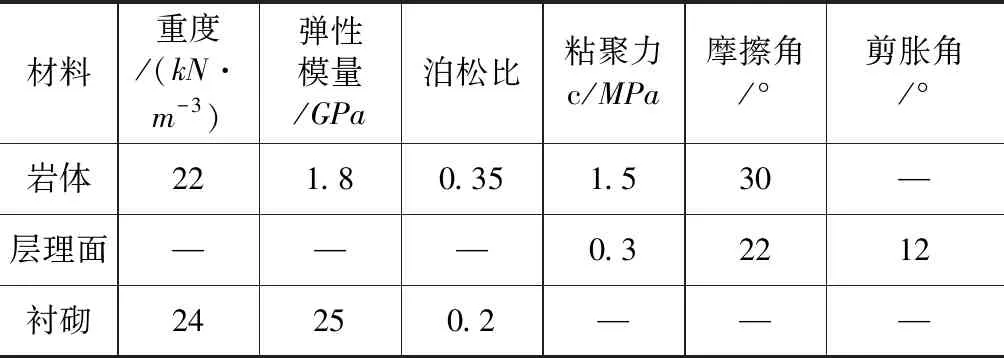
表1 計算參數

2.3 計算假定

本例為模擬實際情況，假設巖層走向與隧道軸線平行，傾向與軸線垂直且以傾角β傾向隧道右側，此時β取45 °；假設圍巖層理面平行均勻分布，層理面間距小，各層理面計算參數相同。

3 結果分析

3.1 圍巖的位移

圍巖開挖后的總位移云圖如圖4所示，圍巖變形計算結果與量測結果對比如圖5所示。計算結果顯示：圍巖總位移云圖呈現明顯不對稱現象，最大位移出現在拱頂與右拱腰，最大值為5.868cm，邊墻變形量最小，仰拱隆起量較大最大可達4cm。現場圍巖監測變形顯示拱頂出現較大沉降，最大7.4cm，與計算值相差1.2cm。計算結果較實測結果位移偏小但具有相似的規律，最大位移均為拱頂和右拱腰部位，隧道右側位移普遍大于左側，較好地模擬了隧道的偏壓作用。

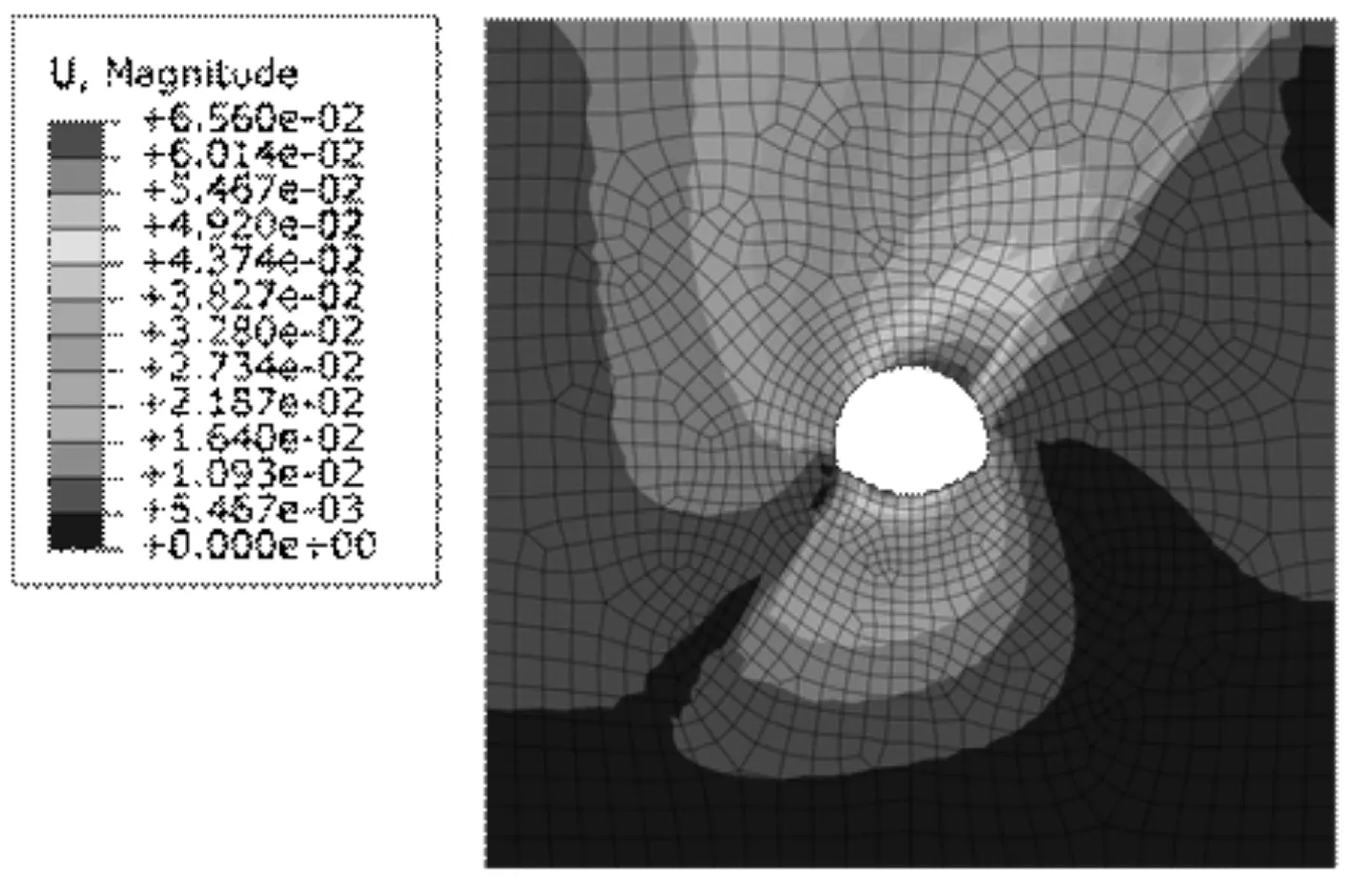
圖4 開挖后總位移云圖(單位：m)

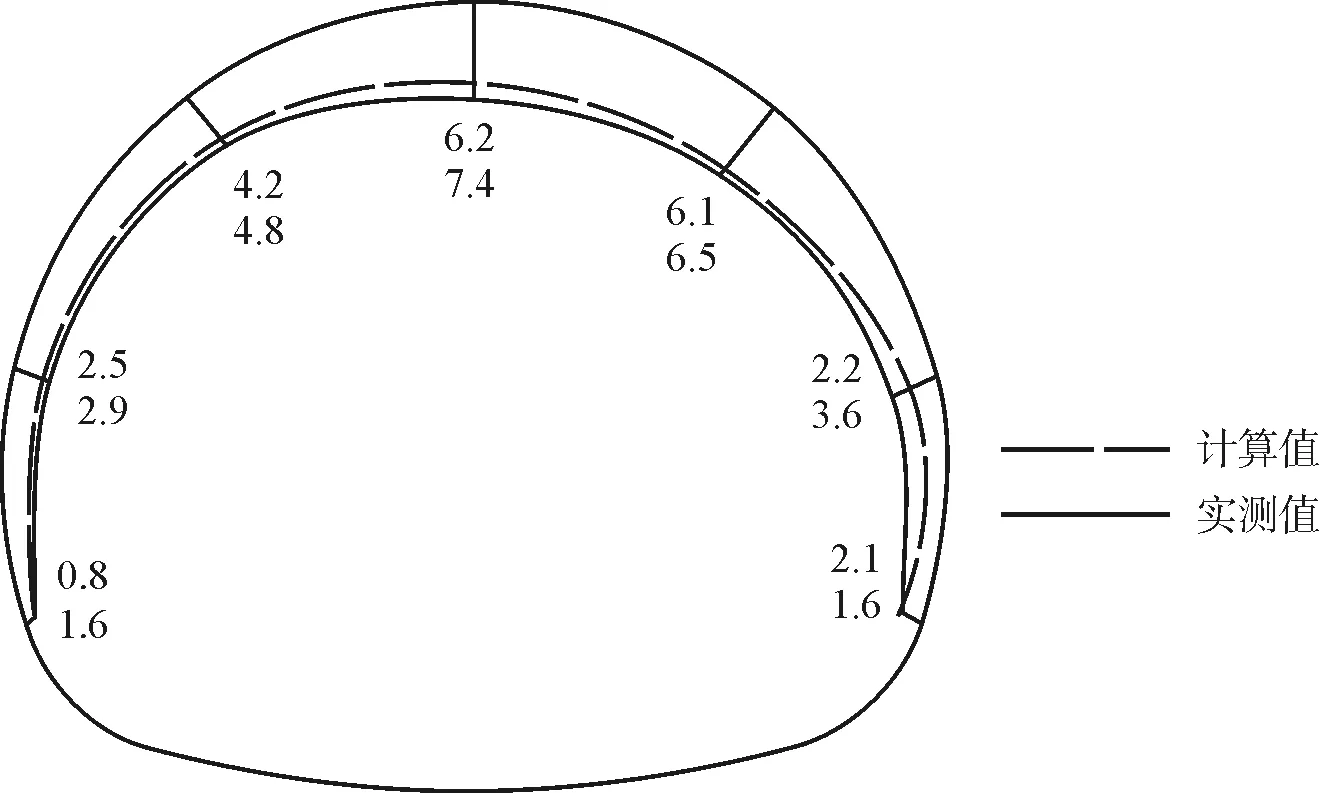
圖5 圍巖位移計算與實測對比(單位：cm)

3.2 圍巖壓力

圍巖壓力計算值與實測值對比如圖6所示。計算結果顯示：右側邊墻和拱腰壓力較大，最大壓力246.9kPa，仰拱壓力最小，拱腳局部壓力較大，如左拱腳150kPa，斷面右側壓力整體大于左側相應位置。實測結果中，拱頂、右側拱腰邊墻壓力較大，最大達到390kPa，與計算差值165kPa，左側和仰拱則較小，實測結果與計算結果具有相似的規律，但偏壓效應更顯著，圍巖兩側壓力差值較大。

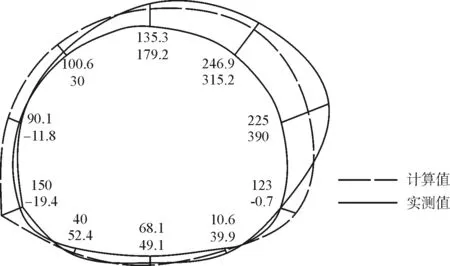
圖6 圍巖壓力計算與實測對比(單位：kPa)

上述結果還表明，由ABAQUS節理材料模型計算得到的結果與現場量測結果具有較好的統一性。以下將進一步利用其研究層理面傾角對隧道及圍巖受力變形的影響。

4 層理面傾角對隧道及圍巖受力變形的影響

為更全面地了解層狀軟巖中圍巖及隧道的受力變形規律，以下將進一步計算分析巖層傾角的影響。此時傾角β分別采用0 °、15 °、30 ° 、45 °、60 °、75 ° 、90 °以及無層面八種工況進行計算分析。

4.1 圍巖破壞區

圖7所示為不同層面傾角時圍巖的塑性區。傾角為0 °和90 °時塑性區對稱，最大塑性應變均位于仰拱部分，其余角度最大塑性應變分布在邊墻和拱腰位置，無層面時圍巖無塑性區，說明層面存在對圍巖破壞有顯著影響。隨著層面傾角的增大，隧道右側塑形區范圍從拱頂逐漸向下轉移到右拱腰、右邊墻，左側塑性區范圍從仰拱向上轉移到左拱腳、左邊墻。

圖7 不同層面傾角下圍巖塑性區分布

4.2 圍巖位移

不同層面傾角下圍巖位移沿拱墻路徑距離分布如圖8所示。各特征點位移隨傾角變化如圖9所示。路徑距離指以左拱腳為起點，右拱腳為終點，沿著洞壁順時針向的弧長距離。

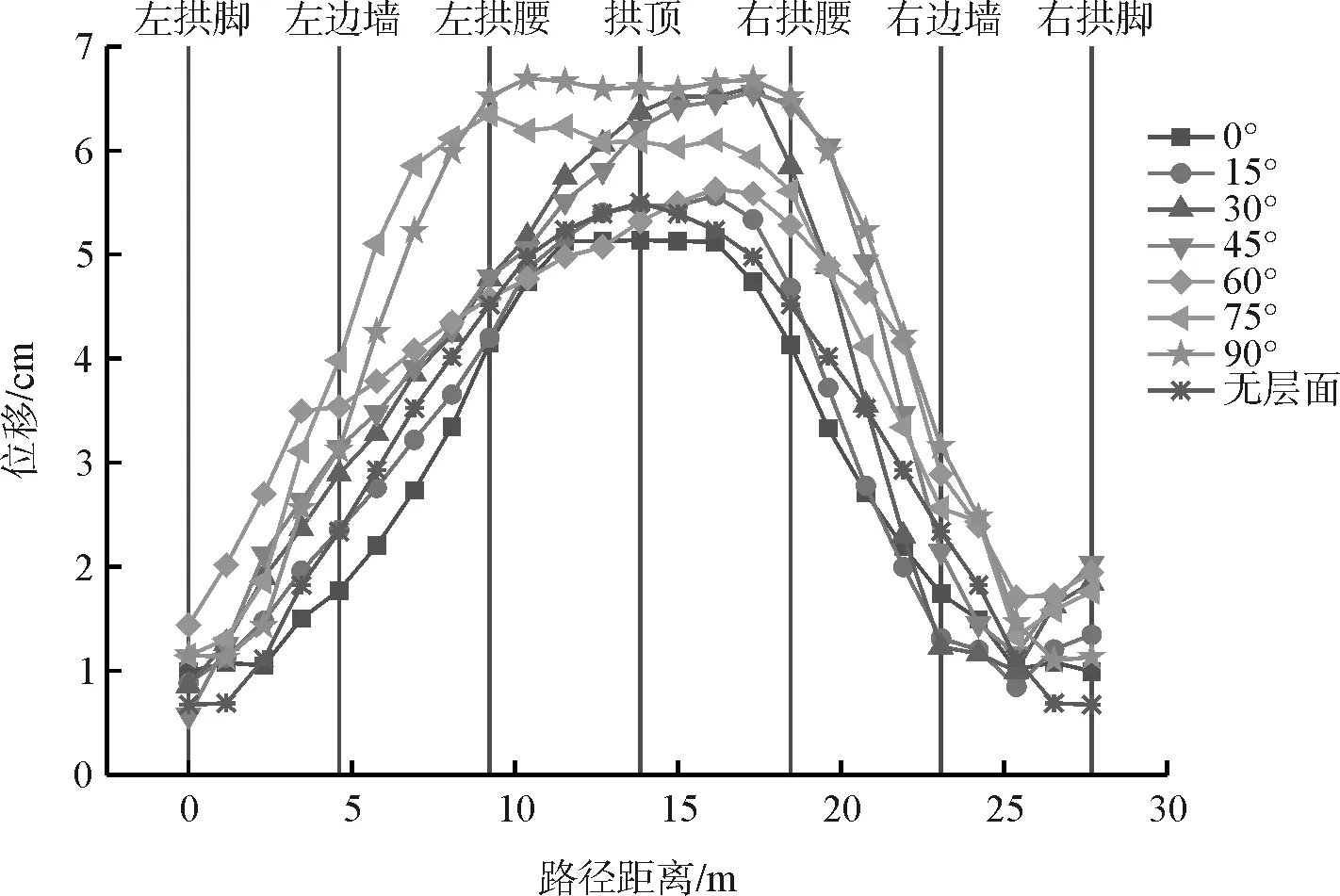
圖8 圍巖位移沿拱墻路徑距離分布曲線

圖9 各特征點位移變化曲線

從圖8、圖9可知：

(1)在同一傾角下，圍巖位移沿著路徑距離先增大后減小，即拱頂和拱腰的位移較兩側拱腳和邊墻大；圍巖左右兩側對應的特征點位移對比，除傾角為0 °和90 °具有對稱性外，其余角度均呈現出不同程度的偏壓現象，整體為斷面右側位移大于左側，值得注意的是，左側邊墻位移均大于右側。

(2)在不同傾角下，隨著層面傾角逐漸增大，圍巖位移呈現逐漸增大的趨勢，即0 °、15 °時位移最小，75 °、90 °時位移最大，無層面時位移大于0 °和15 °而小于其他角度；左右兩側對應特征點位移差值隨傾角增大呈現先增大后減小的趨勢，即位移差值在傾角β∈[ 0°，45°]時從零逐漸增大至最大，約1.5cm，在傾角β∈[ 45°，90°]時，兩側位移差值逐漸減小為零。

4.3 襯砌主應力

ABAQUS中默認應力以受拉為正，受壓為負，通常采用最大主應力評判受拉狀況，采用最小主應力評判受壓狀況。隧道襯砌受力主要為壓應力，因此選取代表性的最小主應力來分析襯砌的應力狀況。不同傾角下襯砌最小主應力沿拱墻路徑距離分布如圖10所示。各特征點最小主應力隨傾角變化如圖11所示。從圖10、圖11可知：

(1)同一傾角下，襯砌受力沿著路徑距離先減小后增大，即拱頂和拱腰的壓應力較小，而兩側拱腳和邊墻的所受應力較大；除傾角為0 °和90 °應力具有對稱性外，其余角度襯砌結構右側所受壓應力普遍大于左側對應特征點。

(2)在不同的傾角下，隨著層面傾角的增大，應力整體呈現逐漸增大的趨勢，其中邊墻和拱腳的增幅較大，而拱頂和拱腰則略有減小；當層面傾角β∈[ 0 °，45 °]時，左右兩側應力差從零逐漸增大，在45 °時差值最大達35MPa，當層面傾角β∈[ 45 °，90 °]時，兩側應力差逐漸減小，直至90 °時重新趨于對稱狀態。以上結果表明，層面傾角從0 °增大到90 °過程中，襯砌結構左右兩側的偏壓效應從弱變強再變弱，在傾角45 °時右側偏壓作用最為顯著。

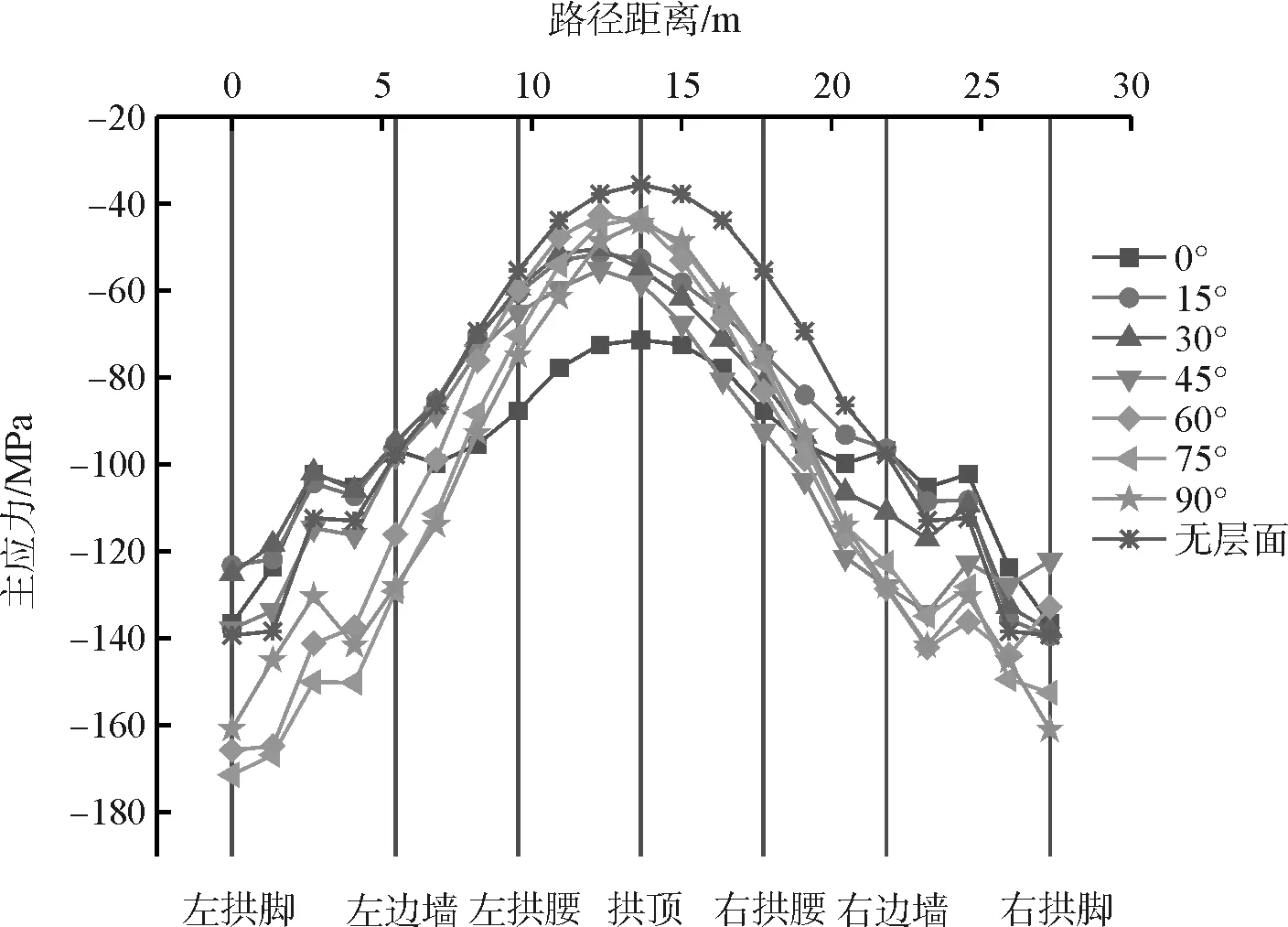
圖10 最小主應力沿拱墻路徑距離分布曲線

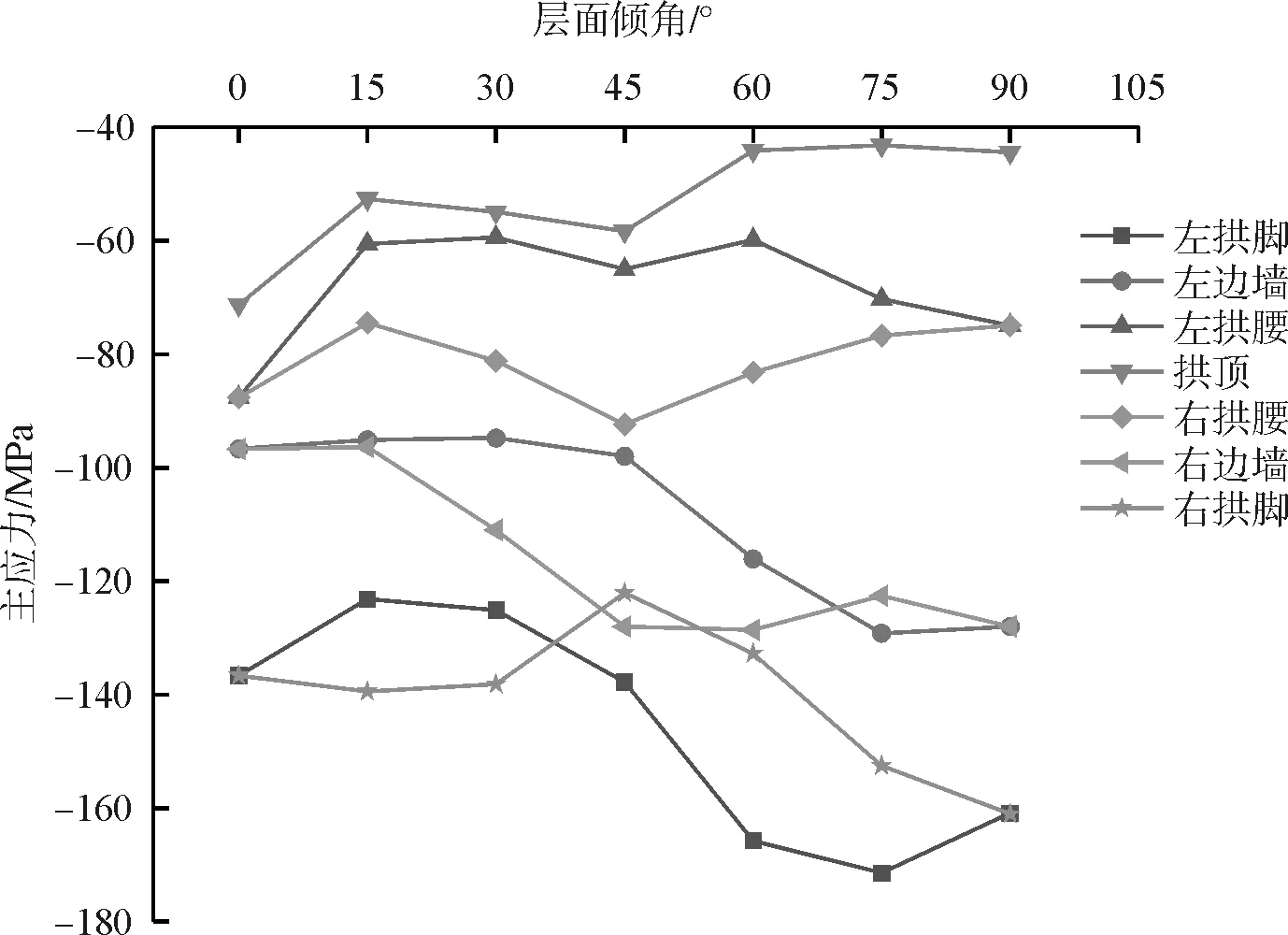
圖11 特征點最小主應力變化曲線

5 結束語

本文通過現場監測數據結合數值模擬結果對比分析，得出以下結論：

(1)隨著傾角的增大，隧道反傾側塑性破壞區范圍從拱頂逐漸向下轉移到右拱腰、右邊墻，順傾側塑性區范圍從仰拱向上轉移到左拱腳、左邊墻。

(2)在巖層傾角一定時，沿著路徑距離，圍巖位移先增大后減小，襯砌壓應力則相反；隧道反傾側的圍巖位移和襯砌受力普遍大于順傾側對應位置，體現出層狀圍巖隧道的偏壓效應。

(3)在不同傾角下，隨著層面傾角的增大，對應特征點圍巖位移和襯砌壓應力均呈現逐漸增大的趨勢，層狀軟巖隧道

的偏壓作用由弱變強再變弱，傾角45 °時偏壓作用最顯著。