基于神經隨機森林的局部空氣質量預測模型

程 蓉，錢雪忠

(江南大學 物聯網工程學院 物聯網技術應用教育部工程研究中心，江蘇 無錫 214122)

0 引 言

空氣質量指數(air quality index，AQI)是用來定量描述空氣質量的無量綱指數，其大小代表空氣的污染程度。主要利用PM2.5、 PM10 、 SO2、 NO2、 CO 、 O3這6項污染物來評價空氣質量。隨著我國經濟的快速發展，大氣污染日益嚴重，霧霾天氣頻頻出現，不僅嚴重威脅著人們的身體健康及地球的氣候系統，還造成了我國經濟利益的巨大損失。同時，對于像南京玄武湖、夫子廟這樣的旅游景區，人來車往，較差的空氣質量也給人們的外出旅行帶來了極大困擾。人們越來越關注空氣質量，希望像天氣預報一樣可以提前知曉，以便安排他們的出行活動計劃并提前做好保護措施。因此，研究局部空氣質量的預測方法，對人們的健康出行以及國家經濟發展意義重大。本文是利用南京市玄武湖地區的歷史天氣數據和空氣質量數據，對該地區下一日的空氣質量進行預測。

目前為止，已經提出了許多預測空氣質量的方法。Shamsoddini A等[1]將隨機森林特征選擇方法與多元線性回歸和多層感知器人工神經網絡相結合，實現空氣中PM2.5、 SO2、 NO2、 CO含量的預測。不僅利用了前一天的空氣污染物的含量，還分析了交通和植被密度對污染物的影響，有效預測了空氣中染污物的濃度。Zhang C等[2]基于Spark集群，提出了隨機森林的空氣質量預測模型，將PM2.5、 PM10、 SO2、 NO2、 CO、 O3作為影響因子，該模型在處理大數據集的時候能夠快速預測AQI，不僅縮短時間還具有可擴展性，但是忽略了AQI的其它影響因素。Junshan W等[3]考慮到天氣模式和空氣質量的時空依賴性，提出一種深度時空集合模型，它是由基于天氣模式的分區策略的集合方法，通過分析各站點間Granger因果關系并將空間數據生成為相對站點和相對區域來發現溫度的相關性，基于深度LSTM的時間預測器3個部分組成，并利用北京35個監測站的數據評估模型，驗證了該模型優于傳統的回歸方法和機器學習。Lifeng W等[4]為了獲取未來空氣質量的趨勢，利用分數階累積的FGM(1,1)模型預測京津冀地區2017年-2020年PM2.5、PM10、SO2、NO2、8-h O3、24-h O3年平均濃度。實驗結果表明，FGM(1,1)模型的預測性能明顯優于傳統的GM(1,1)模型。Gu K等[5]考慮到氣象因子與空氣污染物濃度及幾小時后的空氣質量指數之間的非線性關系，采用1小時中長期預測模型，遞歸地提出了一種啟發式的RAQP模型，并驗證了該模型的有效性以及通用性，它不僅具有較高的預測性能，還可以推導出中間時刻的空氣質量指數。

玄武湖地區的空氣質量不僅受天氣影響，同時也受該地區的交通狀況以及人流量的影響。在車流量和人流量較大的情況下，車子排放的尾氣以及人為的污染對空氣質量預測的影響也很大。所以，空氣質量具有很強的非線性特性。針對空氣質量非線性動態變化的特點，本文提出一種神經隨機森林局部空氣質量預測方法。

1 神經隨機森林局部空氣質量評價模型

1.1 CART回歸樹

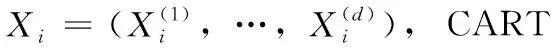
(1)

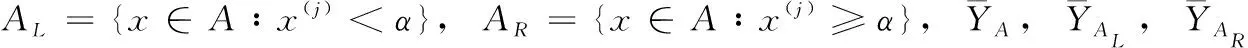
(2)

1.2 隨機森林

隨機森林是由M棵隨機的CART回歸樹組合而成的預測器。對于模型中的第m棵樹，查詢點x處的預測值用t(x;Θm,Dn) 表示，其中Θ1,…,ΘM是隨機變量，分布與一般隨機變量Θ相同。假設Θ1,…,ΘM,Θ與Dn相互獨立，模擬每棵樹結構中引入的額外隨機變量Θ，用于：①在單棵樹生長之前對訓練集進行重新取樣；②通過隨機的CART標準選擇連續的分裂方向；③最后，將所有的樹木組合起來，形成森林。式子如下

(3)

(4)

式(2)和式(4)的本質區別在于式(4)是在隨機選擇的坐標子集Mtry上進行估計的，而不是在整個范圍內 {1,…,d}。 參數mtry是為了減少計算負擔，并在樹之間創建一些多樣性，與n無關，通常將mtry設置為d/3。 此外，由于采用了無替換采樣，每棵樹都是在初始樣本中選取的an個示例的子集上構建的，而不是在整個樣本Dn上。在CART中，當每棵樹到達Kn終端節點時，停止構建單棵樹 (Kn∈{2,…,an},Kn是算法中的一個參數)，這里每棵樹上的葉節點樹等于Kn。

1.3 回歸樹和神經網絡

一般的框架是非參數回歸估計，向其中輸入一個隨機向量X∈[0,1]d， 然后通過估計回歸函數r(x)=Ε[Y|X∈x] 來預測平方可積隨機響應Y∈R。 根據這一思路，假設有一個訓練數據集Dn=((X1,Y1),…,(Xn,Yn))且n≥2， 獨立隨機變量的分布與獨立原型對 (X,Y) 相同。Dn用于構造函數r的估計值r(·;Dn)∶[0,1]d→R。 下文將r(x;Dn) 簡寫成rn(x)。

樹的結構依賴于數據，每棵樹的結構都是不同的。對于一棵回歸樹tn， 它的結構最終取決于數據Dn， 同時，在每個K≥2個終端節點上取恒定值。Tanno R等[6]提出將樹結構中根到葉的路徑由NN表示，形成自適應神經決策樹。在本文中，用同樣的思想將回歸樹與神經網絡結合，但是限制了網絡的層次，將其構建為具有特定連接權重的神經回歸樹。因此，該估計可以被重新解釋為具有兩個隱含層和一個輸出層的三層神經網絡估計。H={H1,…,HK-1} 為構建tn所有超平面的集合，其中jk∈{1,…,d}，αjk∈[0,1]，hk(x)=x(jk)-αjk， 則HK的形式為HK={x∈[0,1]d∶hk(x)=0}。 為了到達查詢點x的葉節點，x落在超平面HK的右邊用+1表示，左邊用-1表示。利用這種表示法，樹估計tn與下面描述的神經網絡相同。

第一個隱藏層。第一個隱層的神經元對應于K-1感知機(每個內部樹節點對應一個),其激活的定義為

τ(hk(x))=τ(x(jk)-αjk)

(5)

其中，τ(u)=2Ιu≥0-1是閾值激活函數，權重向量僅是特征jk的單個單熱矢量， -αjk偏差值。因此，對于樹中的每個分裂，第一層有一個神經元，它的活動編碼輸入x相對于相關分裂的相對位置。總的來說，第一層輸出±1的向量 (τ(h1(x)),…,τ(hK-1(x)))， 它描述了內部的所有決策樹節點(包括x的樹路徑之外的節點)。若x在超平面HK的一側，則τ(hk(x)) 為+1，若在另一側，則τ(hk(x)) 為-1。在這里強調，該層的每個神經元k有且只能連接一個輸入x(jk)， 并且該連接具有權重1和偏移-αjk。 如圖1所示，給出了一個列子。由于第一層的這些特殊激活，第二層可以輕松地構建x的終端單元。

圖1 回歸樹和相應神經元

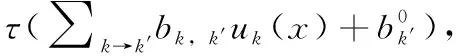
(6)

(7)

(8)

1.4 神經隨機森林

由1.3小節可知，在神經網絡的設置中，重新構造森林的每棵隨機樹估計t(x;Θm,Dn)， 1≤m≤M。 得到的M個網絡是不同的，因為它們對應不同的隨機樹。由上文可知第m個網絡在第一個隱藏層中具有Kn-1個神經元，而在第二個隱藏層中具有Kn個神經元。同時。神經元的連接方式和相關系數取決于Θm和Dn。 將第m棵樹估計t(x;Θm,Dn) 作為神經網絡估計。在Θm和Dn條件下，該網絡神經元的連接方式是固定的，三層的權重和偏移也是固定的。為了保持網絡結構的完整，一旦神經元之間的連接被樹到網絡的映射設計好了，就可以通過最小化樣本Dn上網絡的經驗均方誤差來學習更好的網絡參數。這種額外的訓練可以潛在地改進原始隨機森林的預測。

為了實現梯度反向傳播的訓練，激活函數必須是可微的。因此，用雙曲正切激活函數來代替原始的中繼型激活函數τ(u)=2Iu≥0-1， 即

(9)

取值范圍為[-1,1]。在第一個隱藏層中，每個神經元使用σ1(u)=σ(γ1u)。 在第二層神經網絡中，每個神經元使用σ2(u)=σ(γ2u)。 其中，γ1和γ2是決定雙曲正切激活函數對比度的正超參數：γ1和γ2越大，從-1到1的轉換越快；當γ1和γ2接近無窮大時，連續函數σ1和σ2收斂到閾值函數。雙曲正切激活函數除了提供更好的泛化效果外，還有助于決策邊界的平滑和樹節點隸屬度的松弛。最后，它們允許在不連續階躍激活函數的平滑近似下進行操作。這使得網絡損耗函數在各個參數上都是可微的，并且可以用反向傳播來訓練網絡。

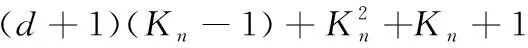
當允許層之間完全連接時，樹結構的松弛可以更進一步。在這種情況下，樹結構僅用作相同大小的完全連接網絡的初始化。在此設置中，屬于樹結構的所有權重都具有非零初始化值，而其它權重是以零開始。在訓練過程中，所有的權重都可以被修改，以便在各個層之間建立任意的連接。與隨機初始化相比，初始樹型參數化提供了很強的誘導偏差，為網絡提供了有效的熱啟動。隨機初始化包含有價值的信息，并在反向傳播訓練之前就已經模擬了CART決策樹的回歸函數。

綜上所述，可以將M個CART類型的樹轉換為M個樹類型的神經網絡。接下來，將描述如何組建M個網絡，將該方法稱為神經隨機森林(下文簡稱為NRF)。

每棵樹型網絡的參數是由網絡相互獨立地進行網絡擬合的，通過將樹型網絡進行獨立的訓練，然后得到一個由M個小神經網絡組成的估計集合r(·;Θm,Dn)， 其中1≤m≤M， 最后求平均形成估計

(10)

如圖2所示。下文，將r(x;Θ1,…,ΘM,Dn) 簡寫為rM,n(x)，rM,n(x) 取決于Θ1,…,ΘM和樣本Dn。

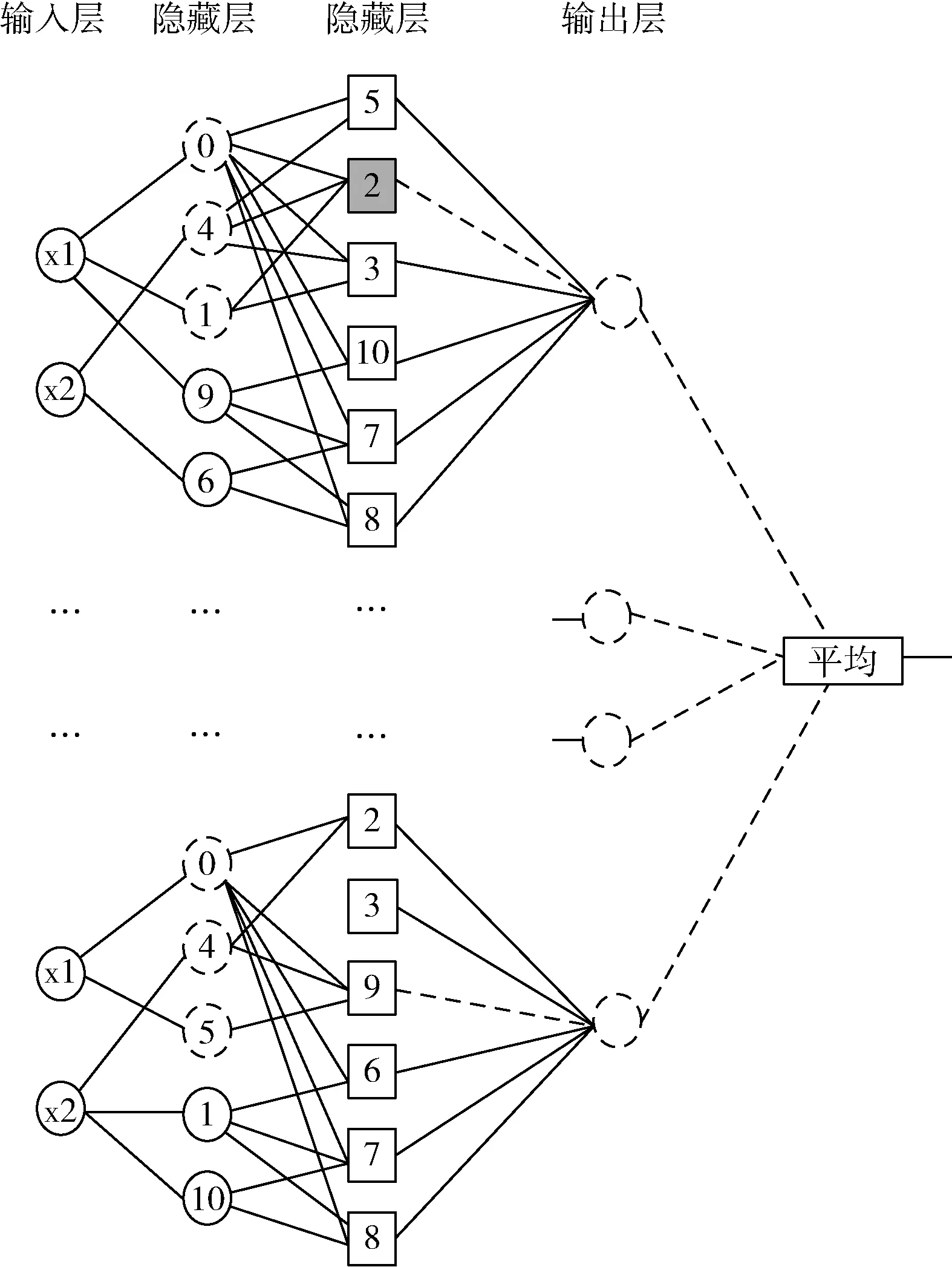
圖2 獨立訓練

下面將介紹在每個小網絡上實施的最小化程序，以及rM,n(x) 的統計特性。考慮到集合中的第m棵隨機樹，用g1=g1(Θm,Dn) 表示輸入向量x=(x(1),…,x(d)) 和第一個隱藏層的Kn-1神經元之間連接的二分圖。同樣的，用g2=g2(Θm,Dn) 表示第一個隱藏層與第二個隱藏層的Kn神經元之間連接的二分圖。

令M(g1) 為d×(Kn-1) 矩陣的集合W1=(aij)， 如果(i,j)?g1則aij=0。 同樣的，令M(g2) 為 (Kn-1)×Kn矩陣的集合W2=(bij)， 如果 (i,j)?g2則bij=0。 第一個隱藏層的參數由g1的權重M(g1) 的矩陣W1和大小為Kn-1 的偏移的列向量b1表示。類似的，第二個隱藏層的參數由g2的權重M(g2) 的矩陣W2和大小為Kn的偏移的列向量b2表示。最后，讓輸出權重和偏移量分別為Wout=(w1,…,wKn)Τ∈RKn(Τ表示轉置)和bout∈R。 因此，指定第m個網絡的參數由“向量”表示

λ=(W1,b1,W2,b2,Wout,bout)∈
M(g1)×RKn-1×M(g2)×RKn×RKn×R

(11)

這里，為了保持一致性，限制這些參數的變化范圍。對于給定的矩陣M， 符號 |M| 表示M的元素的絕對值矩陣。假設存在一個正常數C1， 這樣

(12)

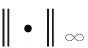
Λ(Θm,Dn)={λ=(W1,b1,W2,b2,Wout,bout)}

(13)

第m個神經網絡實現了這種形式的函數

(14)

其中，λ∈Λ(Θm,Dn)， 并且σ1和σ2是按元素來應用的。我們的目的是利用數據Dn來調整參數λ， 從而使所得到的網絡實現的函數可以很好地估計r。 使

F(Θm,Dn)={fλ∶λ∈Λ(Θm,Dn)}

(15)

其中，m∈{1,…,M}。 算法通過最小化經驗誤差來構造回歸函數估計r(·;Θm,Dn)

(16)

在F(Θm,Dn) 中的函數f， 即f∈F(Θm,Dn) 有

Jn(r(·;Θm,Dn))≤Jn(f)

(17)

在這里，假設存在一個最小值，盡管它不一定是唯一的。在不存在最小值的情況下，可以使用誤差任意接近下限的函數來執行相同的分析，但是為了簡單起見，本文堅持存在的假設。通過重復這個最小化過程，對于每個m∈{1,…,M}， 可以得到隨機估計的集合r(·;Θ1,Dn),…,r(·;ΘM,Dn)， 它們被合并求平均值形成了估計

(18)

估計rM,n只是隨機森林估計tM,n對神經網絡框架的推廣，由于雙曲正切激活函數的存在，額外松弛到模糊樹節點隸屬度：樣本不僅每個分裂和一個最終葉子落入一個方向，而且同時分成幾個樹枝和葉子。

2 實驗設計與結果分析

2.1 數據來源及選擇

NRF模型是對原始隨機森林算法的優化，為了驗證NRF模型的性能，本文在UCI機器學習倉庫中選取4個標準回歸數據集，分別是汽車MPG數據集(auto_mpg)、社區犯罪數據集(communities crime)、森林火災數據集(forest fires)以及波士頓房價數據集(Boston House Price)作為樣本數據集，并將樣本數據按照50∶25∶25的比例分為訓練集、驗證集和測試集，分別在NRF模型、RF模型和NN模型中運行。這里，隨機森林采用樹木數量為25，最大深度為6的最優參數組合。表1展示了不同數據集在NRF、RF和NN模型上運行的均方根誤差(RMSE)。

表1 NRF、RF、NN在不同數據集上的RMSE

從表1可看出，NN模型在大部分數據集中都沒有達到與NRF模型和RF模型一樣的預測效果。同時，NRF模型在不同數據集中的RMSE都明顯小于RF模型的RMSE。由此可見，NRF模型的預測效果要優于RF模型和NN模型，取得了不錯的效果。接下來，本文將NRF方法應用于實際問題，利用南京市玄武湖地區的歷史天氣和空氣質量數據，來預測該地區下一日的AQI指數。

本實驗采用的數據是來自南京市玄武湖監測站提供的空氣質量歷史監測數據。實驗選取了2013年10月1日-2019年3月31日玄武湖地區的空氣質量數據作為實驗樣本數據，共2008條，將樣本數據按50∶25∶25的比例分為訓練集、驗證集和測試集。

圖3和圖4分別展示了南京市玄武湖地區AQI指數日均值和月均值時序變化規律。從圖中可以看出，AQI指數日均值和月均值基本上服從正態分布規律，更好契合了該算法。從圖3可看出，AQI指數日均值隨著時間的推移出現峰谷型變化。從圖4可看出，AQI指數呈春冬高、夏秋低的特點，12月和1月是AQI指數高發月，這也是把季節作為一項特征的原因。

如表2所示，選取氣象條件、大氣污染、人類污染和季節4個方面共33個相關特征因素。其中，溫度、氣壓、紫外線、濕度、降水量、大氣污染物濃度以及人流量車流量屬于數值型特征用“real”表示，其余均屬于非數值型。在處理非數值型特征時，本文對其進行量化：將非數值型特征轉化為離散的數值型特征，并放入“[]”，以此表示取值范圍。如“(Before_)weather”的取值為“[0,1,2,3,4,5]”，代表6種天氣狀況：晴、多云、陰、雨、雪、霧；“(Before_)Direction”的取值為“[0,1,2,3,4,5,6,7]”，代表8種風向：東風、東北風、東南風、南風、西南風、西風、西北風、北風；“(Before_)speed”的取值為“[0,1,2,3,4,5]”，代表6種風力類型：1～2級、3～4級、4～5級、5～6級、6～7級、7～8級;“Season”的取值為“[1,2,3,4]”，代表初、夏、秋、冬4個季節。

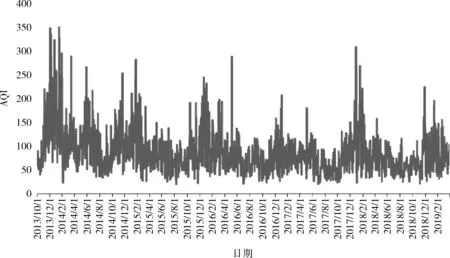
圖3 玄武湖地區AQI指數日均值時序規律

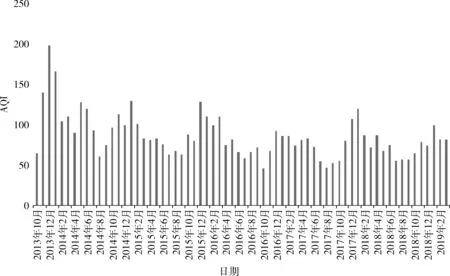
圖4 玄武湖地區AQI指數月均值時序規律

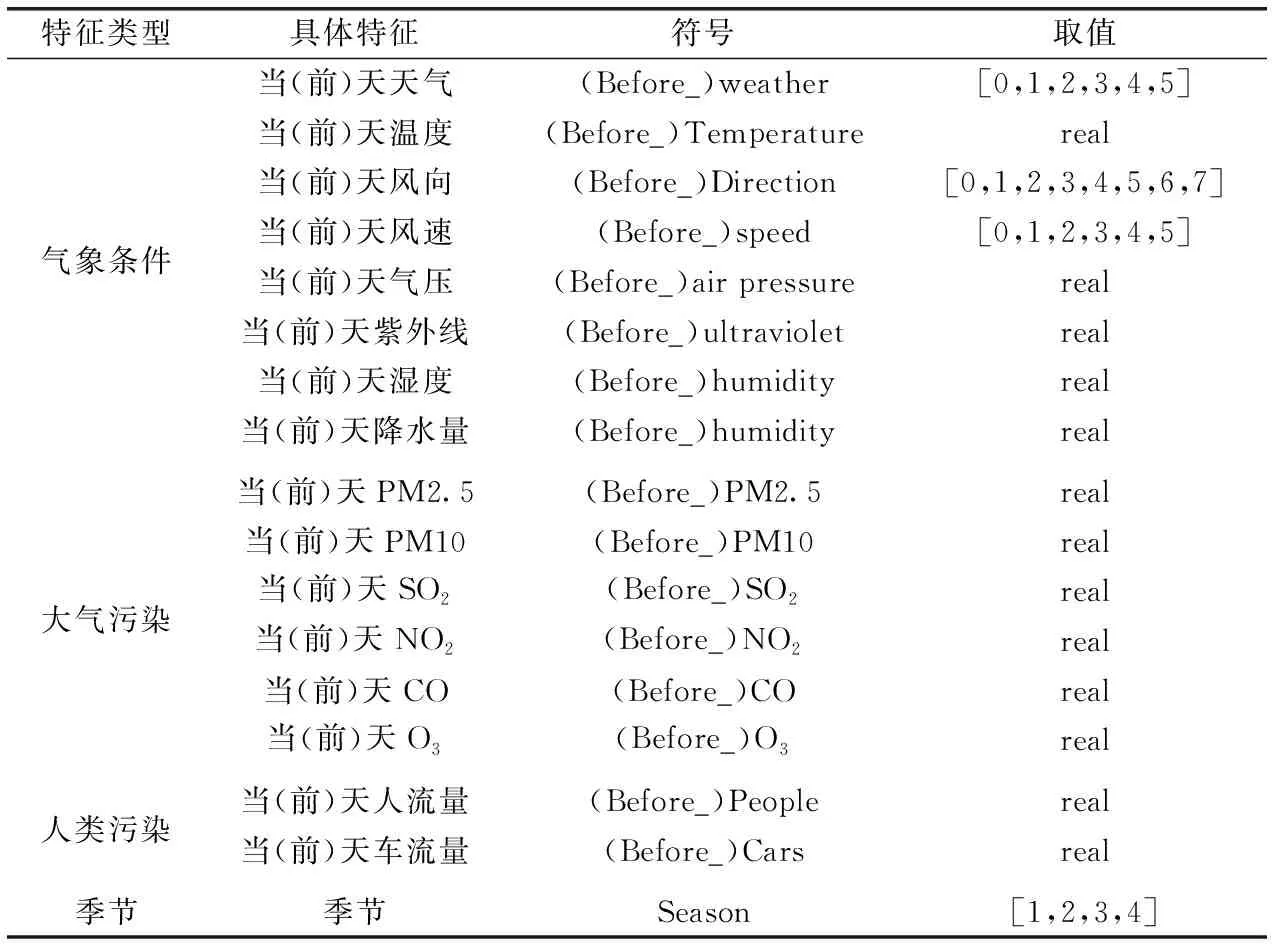
表2 特征因素的選取

2.2 模型評價指標

為衡量預測模型的穩定性和適應性，本文選取了擬合度(R2)、均方根誤差(RMSE)這兩個指標對模型進行評價。公式如下

(19)

(20)

2.3 實驗結果與分析

在構造NRF模型時，采用樹木數量為25，最大深度為6的最優參數組合，NRF層之間采用的是完全連接，即初始化網絡權重，這樣就有較少的權重需要優化，并且每層具有相同數量的神經元。首先使用scikit-learn運行隨機森林，在此基礎上，將所有分割方向和分割位置的集合用于構建神經網絡初始化參數，然后再使用TensorFlow框架訓練NRF模型。

在學習NRF和NN網絡模型時，優化目標是最小化某些訓練集上的均方誤差。在神經網絡訓練中，是通過使用基于迭代梯度的優化算法來實現的。該算法遍歷訓練集，生成預測，然后將產生的誤差信號相對于所有單獨的網絡參數的梯度傳播回網絡。更新網絡參數，可以減小該誤差，慢慢地模型學會了生成正確的預測。本實驗中，batchsize大小默認為32，隨機初始化權重分別默認為β1=0.9，β2=0.999，ε=1e-08， 以及初始學習率默認為0.001。在每次訓練開始時，都會對訓練集進行重新排序和分配，以避免過度擬合。

每棵神經樹的神經網絡都訓練迭代100次。在訓練過程中，每完成一次訓練后都會監測訓練損失和驗證損失，最后選擇的參數是在100次訓練過程中給出最小驗證誤差的參數。同時,γ2使用較小的值比γ1使用較小的值 (γ2，γ1分別是第二和第一隱藏層中的激活函數的初始對比度參數)更有用。這是因為有一個相對較小的對比度γ2， 激活函數從-1到+1的轉變更平滑，并且更強的梯度信號到達反向傳播訓練中的第一隱藏層。因此,本實驗使用γ1=100和γ2=1。

為了說明訓練行為，將NRF模型與RF模型和NN模型的訓練誤差和驗證誤差進行了對比，如圖5所示。

圖5 訓練和驗證誤差對比

從圖5中可以看出，NRF模型在訓練期間的RMSE明顯低于驗證期間的RMSE。同時，NRF模型不管是訓練RMSE還是驗證RMSE都低于RF模型對應的RMSE，說明了NRF具備較好的學習能力和泛化能力。將NRF與參數和層數完全相同的NN對比，很顯然，NRF模型在訓練集和驗證集上的RMSE均低于NN模型。由此可見，NRF模型優于RF模型和NN模型。

利用測試集對訓練好的模型進行AQI指數的預測。圖6 給出了NRF模型的測試效果，預測值與實際測試值擬合較好。

圖6 測試效果

圖7展示了模型預測值和實際值的線性擬合結構，其中相關系數為0.952，擬合度R2達到了0.973。圖8是隨機森林(RF)、神經網絡(NN)、支持向量機回歸(SVR)、線性回歸(LR)、LSTM神經網絡(LSTM)模型與NRF模型的預測誤差對比圖，RF和LR的誤差在(-90,60)范圍內，NN和SVR的誤差在(-280,70)之間，LSTM的誤差在(-60,270)之間，NRF的誤差則在(-70,30)之間。相比較其它模型，NRF的預測誤差范圍最小，分布也比較均勻集中。具體性能指標對比見表3。

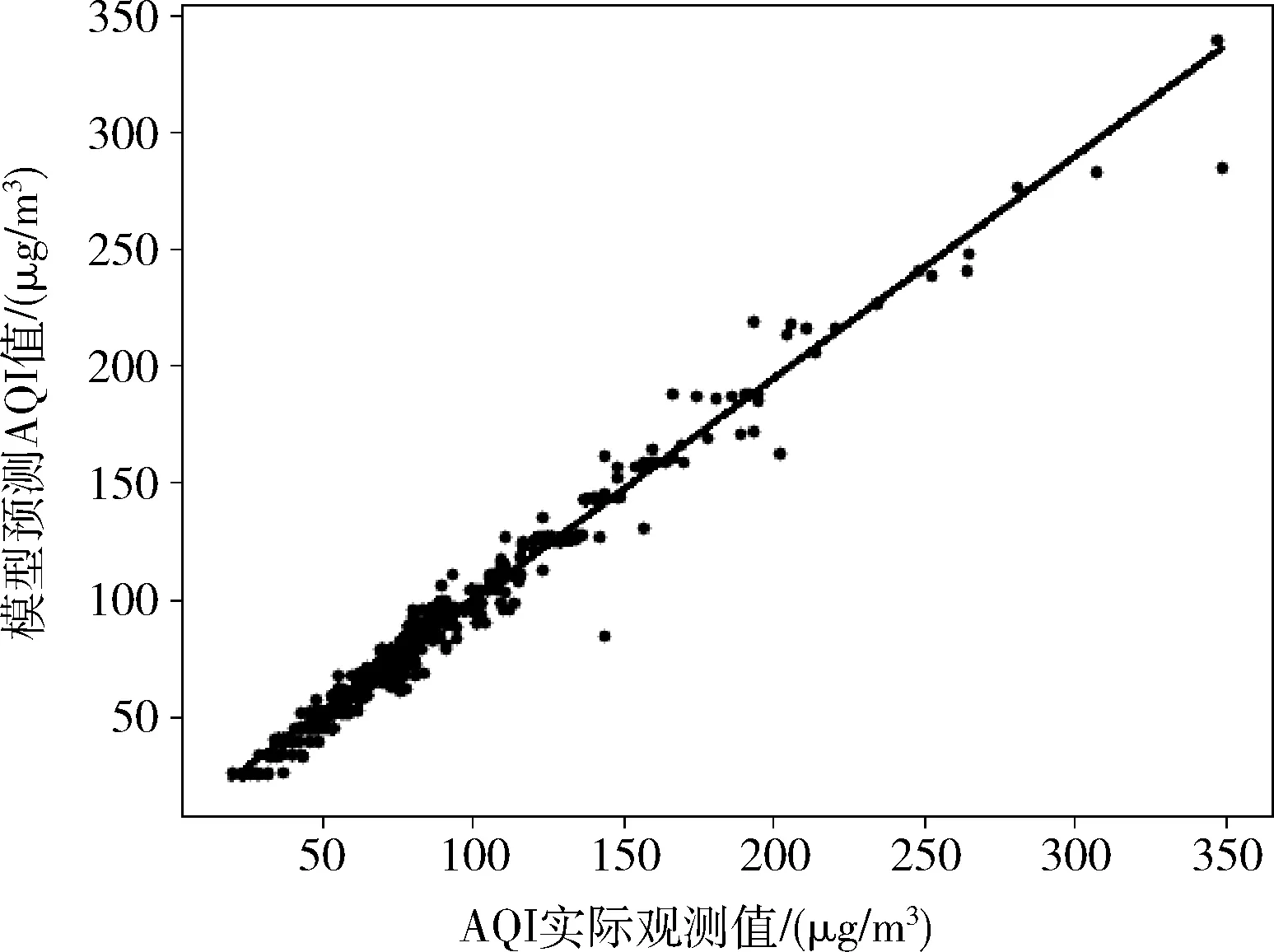
圖7 AQI預測值與實際值相關性分析

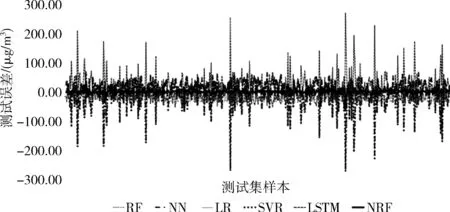
圖8 不同模型的測試誤差

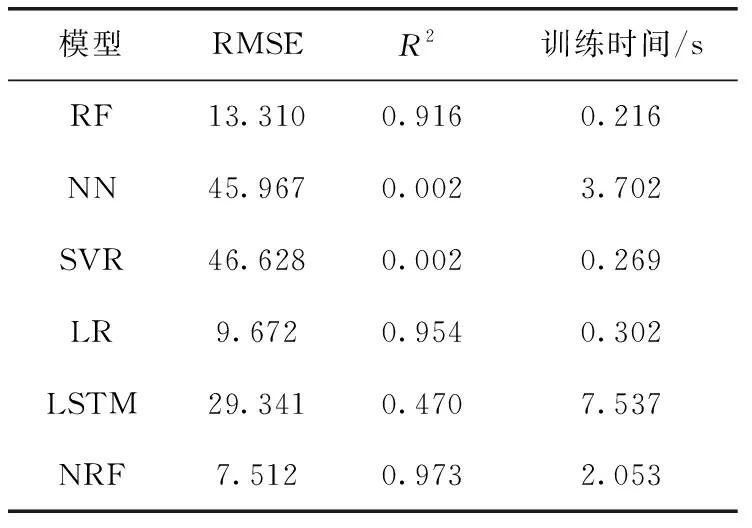
表3 不同模型的預測結果對比

通過表3比較發現，NRF在模型精度方面明顯優于其它方法。NRF模型的均方根誤差RMSE為7.512，相比較RF模型的13.310和NN模型的45.967，分別降低了5.798和38.455，同時NRF模型的擬合度R2也高于RF和NN，說明NRF不易過擬合，并且具備較好的學習能力和泛化能力。而NN模型存在計算量大、學習效率低，容易過擬合等問題。同時，NRF模型的RMSE明顯高于SVR模型、LR模型和LSTM模型。在模型的運行效率方面，NRF模型的訓練時間高于RF模型，低于NN模型，那是因為NRF模型需要對每棵神經樹進行單獨安裝，并單獨進行訓練，每次訓練迭代100次，所以導致NRF模型訓練時間高于RF模型。但是，NRF連接網絡使用的是森林結構，并且提供了智能初始化作為熱啟動，可以有效降低過度擬合，同時完全連接網絡優化速度快，在GPU上進行訓練時，使用密集矩陣乘法，將不存在的連接的條目強制為0，因此也大大減少了訓練時間，故訓練時間低于NN模型。同時，NRF模型的擬合度明顯高于RF模型的擬合度，說明NRF模型對數據的擬合效果更好，可以更準確預測該地區下一日空氣質量。從整體來看，NRF模型的預測效果優于RF模型。綜合比較預測結果，NRF模型在空氣質量指數預測問題上的效果優于RF、NN、SVR、LR、LSTM，具有較高的準確率，能夠很好地解決復雜的非線性問題。

NRF模型結合了RF模型和NN模型的優點，結構簡單易于理解、參數易于調節、模型實現簡單，且不需要對數據進行歸一化處理和交叉驗證，模型的精度高，擬合效果也更好。所以，NRF在綜合性能上具有一定的優勢。綜上所述，本文使用的方法具有可行性與有效性，能夠很好地滿足玄武湖地區下一日空氣質量的預測任務。

3 結束語

基于優化的隨機森林的局部空氣質量預測模型，通過將隨機回歸樹重構為具有兩個隱藏層和一個輸出層的神經網絡回歸樹，然后再將這些神經網絡回歸樹進行獨立訓練，最后合并求平均形成一個由M個小網絡構成的神經隨機森林。該神經隨機森林結合了隨機森林與神經網絡的優點，具有較高的擬合度，并且性能穩定，具有很好的泛化能力，可以很好地應用在局部空氣質量的預測上。NRF模型是對原始隨機森林RF的優化，有效提高了預測精度。同時，由于NRF模型的特定歸納偏差，不管在哪一個數據集上，都可以取得令人滿意的預測結果。因此，在實際應用中，本文為城市環境空氣質量評價提供了一種高效準確的處理辦法。下一步的工作是改變每棵神經網絡回歸樹的訓練方式，將它們放在一起訓練并研究該訓練方法對整個模型的影響，從而提高模型的運行效率。