基于分布式存儲(chǔ)的OHitchhiker碼

李 慧，李貴洋，胡金平，周 悅，江小玉，韓鴻宇

(四川師范大學(xué) 計(jì)算機(jī)科學(xué)學(xué)院，四川 成都 610101)

0 引 言

作為云計(jì)算基礎(chǔ)的大規(guī)模分布式容錯(cuò)存儲(chǔ)系統(tǒng)[1,2]，采用糾刪碼作為數(shù)據(jù)冗余技術(shù)能比多副本技術(shù)以更低的存儲(chǔ)開銷獲得相同的數(shù)據(jù)可靠性。例如Google文件系統(tǒng)[3]部署RS(9,6)碼、Baidu Atlas云平臺(tái)[4]部署RS(12,8)碼、Facebook 存儲(chǔ)系統(tǒng)[5]部署RS(14,10)碼，Hadoop分布式文件系統(tǒng)[6]則提供多種參數(shù)的RS (n,k) 碼，以供用戶選擇。在分布式存儲(chǔ)系統(tǒng)中，節(jié)點(diǎn)失效是一種常態(tài)。比如在Facebook的3000個(gè)節(jié)點(diǎn)生產(chǎn)集群中，每天發(fā)生高達(dá)20個(gè)或更多節(jié)點(diǎn)故障[7,8]，從而觸發(fā)修復(fù)作業(yè)，導(dǎo)致修復(fù)帶寬占比高達(dá)10%-20%。過高的修復(fù)帶寬使得糾刪碼技術(shù)在實(shí)際中的應(yīng)用受到限制，所以如何降低修復(fù)帶寬問題成為糾刪碼的研究熱點(diǎn)之一[9,10]。

Reed-Solomon碼[11]常常是分布式存儲(chǔ)系統(tǒng)的標(biāo)準(zhǔn)設(shè)計(jì)選擇，但是其高昂的修復(fù)成本被認(rèn)為是高存儲(chǔ)效率和高可靠性不可避免的代價(jià)。為降低修復(fù)成本，Rashmi等提出了Piggybacking設(shè)計(jì)框架，保證在較低的存儲(chǔ)開銷下，進(jìn)一步減少修復(fù)帶寬；Rashmi等對(duì)Piggybacking框架進(jìn)一步完善補(bǔ)充[12]。基于Piggybacking框架，Rashmi等又提出了一種在工程中易于實(shí)現(xiàn)的雙條帶結(jié)構(gòu)Hitchhiker碼[13]。Hitchhiker碼不僅具有RS碼的通用性，同時(shí)適用于各種 (n,k) 參數(shù)配置，在Facebook存儲(chǔ)系統(tǒng)和Hadoop分布式系統(tǒng)中已部署實(shí)現(xiàn)。

本文基于Hitchhiker碼，提出一種結(jié)合不同參數(shù) (n,k) 值動(dòng)態(tài)選擇的數(shù)據(jù)分配算法DSDA(dynamic selection of data allocation algorithm)，構(gòu)造出一種最優(yōu)分配的OHitchhiker碼，可以針對(duì)不同 (n,k) 值選擇具有最小修復(fù)代價(jià)的編碼結(jié)構(gòu)，進(jìn)一步降低下載帶寬。

1 相關(guān)工作

本文定義了如下參數(shù)，見表1。

表1 參數(shù)

糾刪碼可通過 (n,k) 兩個(gè)參數(shù)表示，其包含編碼、解碼兩個(gè)過程。編碼是指通過k個(gè)數(shù)據(jù)塊 {A1,…,Ak} 計(jì)算產(chǎn)生n個(gè)塊 {C1,…,Cn}。 解碼是指當(dāng) {C1,…,Cn} 中不大于n-k個(gè)塊失效時(shí)，則可任選其中k個(gè)未失效的塊，計(jì)算恢復(fù)失效塊數(shù)據(jù)。分布式系統(tǒng)中使用的糾刪碼通常滿足兩個(gè)性質(zhì)：①最大距離可分性(MDS性質(zhì))，即能實(shí)現(xiàn)所需的容錯(cuò)基礎(chǔ)上保證存儲(chǔ)冗余也最小；②系統(tǒng)性，即編碼后的n個(gè)節(jié)點(diǎn)中，有k個(gè)節(jié)點(diǎn)存儲(chǔ)原始數(shù)據(jù)，則r個(gè)節(jié)點(diǎn)存儲(chǔ)校驗(yàn)數(shù)據(jù)。

通常，我們將n個(gè)節(jié)點(diǎn)(數(shù)據(jù)節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn))統(tǒng)稱為一個(gè)條帶，條帶中的節(jié)點(diǎn)將會(huì)被分到不同的機(jī)架(如存儲(chǔ)服務(wù)器)上去分布式存儲(chǔ)。由于數(shù)據(jù)的分布式存儲(chǔ)，導(dǎo)致節(jié)點(diǎn)故障頻率增高，修復(fù)過程也就頻繁發(fā)生。所謂的修復(fù)過程，傳統(tǒng)的糾刪碼在分布式存儲(chǔ)系統(tǒng)環(huán)境中不是最優(yōu)的：因?yàn)楫?dāng)一個(gè)節(jié)點(diǎn)失效時(shí)，通常會(huì)從存儲(chǔ)在該節(jié)點(diǎn)中的每個(gè)子條帶中丟失一個(gè)塊。以RS碼和Hitchhiker碼為例進(jìn)行分析，Hitchhiker碼編碼思想：在雙條帶RS碼上利用異或操作將第一子條帶原始數(shù)據(jù)塊 {a1,…,ak} 附加在第二子條帶的校驗(yàn)數(shù)據(jù)塊上，以此減少修復(fù)成本。Hitchhiker碼主要采用均分的數(shù)據(jù)分配思想。由于數(shù)據(jù)分配算法的不同，Hitchhiker碼可細(xì)分為兩種：Hitchhiker-XOR碼和Hitchhiker-XOR+碼。

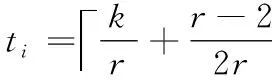
當(dāng)一個(gè)系統(tǒng)節(jié)點(diǎn)Nodei失效時(shí)，3種碼的修復(fù)下載量：雙條帶RS碼需要下載2k個(gè)數(shù)據(jù)塊；當(dāng)Nodei中ai∈Sj,(i=1,…,k),(j=1,…,r-1)， Hitchhiker-XOR碼和Hitchhiker-XOR+碼都需要下載k+|Sr| 個(gè)數(shù)據(jù)塊；當(dāng)Nodei中ai∈Sr時(shí)，Hitchhiker-XOR+碼則需要下載k+|Sr|+r-2個(gè)數(shù)據(jù)塊。

以參數(shù) (n,k)=(13,10) 為例，當(dāng)節(jié)點(diǎn)Node8失效時(shí)，此時(shí)RS碼、Hitchhiker-XOR和Hitchhiker-XOR+碼的修復(fù)下載情況，如圖1所示。

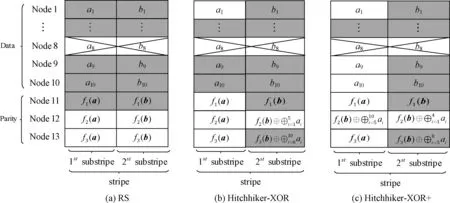
圖1 (n,k)=(13,10) 3種糾刪碼

從圖1中可以發(fā)現(xiàn)，Hitchhiker-XOR碼將原數(shù)據(jù)塊 {a1,…,a10} 均分成2份，其分塊情況S={5,5}， 其中S1={a1,…,a5},S2={a6,…,a10}， Hitchhiker-XOR+碼則分成3份，分塊情況S={4,4,2}， 其中S1={a1,a2,a3,a4},S2={a5,a6,a7,a8},S3={a9,a10}。 由于不同的編碼結(jié)構(gòu)，系統(tǒng)節(jié)點(diǎn)修復(fù)帶寬存在差異。

2 OHitchhiker碼

本文提出一種最優(yōu)分配的OHitchhiker編碼，通過在編碼的分配環(huán)節(jié)引入一種高效的動(dòng)態(tài)算法，使得OHitchhiker編碼可以針對(duì)不同 (n,k) 值選擇具有最小修復(fù)代價(jià)的編碼結(jié)構(gòu)。

2.1 動(dòng)態(tài)選擇的數(shù)據(jù)分配算法

根據(jù)數(shù)學(xué)推理和OHitchhiker碼的特征，本文提出了動(dòng)態(tài)選擇的數(shù)據(jù)分配算法DSDA(dynamic selection of data allocation algorithm)。DSDA執(zhí)行兩步分配：均分分配和移動(dòng)分配。

為了更好地描述根據(jù)不同(n,k)值來動(dòng)態(tài)選擇最優(yōu)的分配，現(xiàn)引入兩個(gè)參數(shù)q和p， 其中q表示商，即q=k/r；p表示余數(shù)，即p=k%r。

均分分配：將原始數(shù)據(jù)塊 {a1,…,ak} 劃分成r份，每一份存放的數(shù)據(jù)塊數(shù)為ti=q,(i=1,…,r)； 當(dāng)k不能整除r時(shí)，將余下數(shù)據(jù)塊存放到第r份中，即tr=q+p。 分塊情況S={|S1|,…,|Sr|}; 其中 |Si|=ti,(i=1,…,r-1),|Sr|=tr。 此時(shí)系統(tǒng)節(jié)點(diǎn)數(shù)據(jù)aj和bj,(j=1,…,k) 的修復(fù)下載量為

(1)

此時(shí)系統(tǒng)節(jié)點(diǎn)的平均修復(fù)數(shù)據(jù)下載量為

(2)

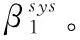
將兩者的平均修復(fù)數(shù)據(jù)下載量相減，得到

(3)

當(dāng)Δβsys>0時(shí)，即表示移動(dòng)后的下載量更少，則需要移動(dòng)分配，進(jìn)一步降低修復(fù)成本。

移動(dòng)分配：即當(dāng)Δβsys>0時(shí)，則需要將Sr中的數(shù)據(jù)移動(dòng)一塊到Si,(i=1,…,r-1) 中，再更新p=p-1， 循環(huán)m次移動(dòng)后，直到Δβsys>0不滿足為止。最后得到分塊情況S={|S1|,…,|Sr|}; 其中|Si|=q+1, |Sj|=q， |Sr|=q+p-m,(i=1,…,m;j=m+1,…,r-1)。

根據(jù)以上原則，動(dòng)態(tài)選擇數(shù)據(jù)分配算法DSDA的過程如算法1所示：①初始分塊，得到平均分塊數(shù)q和剩余分塊數(shù)p；②均分分配，將原數(shù)據(jù) {a1,…,ak} 劃分成r份；③移動(dòng)分配，當(dāng)Δβsys>0時(shí)，將Sr中的數(shù)據(jù)移一塊到Sj,(j=1,…,r-1) 中，更新p， 循環(huán)直到Δβsys≤0； ④分配結(jié)束，輸出分塊情況S。

算法1： 動(dòng)態(tài)選擇的數(shù)據(jù)分配算法DSDA

輸入：k—數(shù)據(jù)節(jié)點(diǎn)

r—校驗(yàn)節(jié)點(diǎn)數(shù)

輸出：

S—數(shù)據(jù)分配情況

過程：

步驟1 初始分塊：

q=k/r,p=k%r

步驟2 均分分配：

Foriin len (S)

Si←q

IFq>0 Then

Sr←q+p

步驟3 移動(dòng)分配：

While Δβsys>0

Si←Sr,q--

步驟4 結(jié)束， 輸出S。

動(dòng)態(tài)選擇數(shù)據(jù)分配算法DSDA緊密契合了OHitchhiker碼的雙條帶結(jié)構(gòu)特性，使得OHitchhiker碼在修復(fù)過程中首先實(shí)現(xiàn)全局均分分配，大幅度降低修復(fù)帶寬；然后通過不同 (n,k) 參數(shù)判斷執(zhí)行移動(dòng)分配，達(dá)到最優(yōu)動(dòng)態(tài)選擇模式，從而降低修復(fù)時(shí)所需的總數(shù)據(jù)下載量，保證系統(tǒng)節(jié)點(diǎn)的平均修復(fù)帶寬最低。

2.2 OHitchhiker編碼結(jié)構(gòu)

OHitchhiker碼繼承Hitchhiker碼的雙條帶結(jié)構(gòu)，利用異或操作將數(shù)據(jù)節(jié)點(diǎn)塊疊加在校驗(yàn)節(jié)點(diǎn)上的方式，根據(jù)動(dòng)態(tài)選擇的數(shù)據(jù)分配算法，將系統(tǒng)節(jié)點(diǎn)的修復(fù)成本降到最低。

OHitchhiker編碼過程分成如下3步：

(1)利用RS編碼，將原始k個(gè)數(shù)據(jù) {a1,…,ak} 進(jìn)行編碼，計(jì)算產(chǎn)生r個(gè)校驗(yàn)塊；然后將數(shù)據(jù)塊和校驗(yàn)塊，共n個(gè)塊 {a1,…,ak,f1(a),…fr(a)} 分布式存儲(chǔ)在n個(gè)節(jié)點(diǎn)中，即為一個(gè)條帶；

(2)根據(jù)DSDA分配算法，首先均分分配，將原始數(shù)據(jù)塊 {a1,…,ak} 劃分成r份；然后根據(jù)式(3)判斷Δβsys， 當(dāng)Δβsys>0時(shí)，進(jìn)行移動(dòng)分配；得到分塊情況S={|S1|,…,|Sr|}; 其中 |Si|=q+1,|Sj|=q， |Sr|=q+p-m,(i=1,…,m;j=m+1,…,r-1)；

(3)利用RS編碼生成兩個(gè)條帶拼接合成一個(gè)條帶，細(xì)分為第一子條帶 {a1,…,ak,f1(a),…fr(a)} 和第二子條帶 {b1,…,bk,f1(b),…fr(b)}。 通過將第一子條帶的系統(tǒng)節(jié)點(diǎn)數(shù)據(jù) {a1,…,ak} 分塊疊加在第二子條帶的校驗(yàn)節(jié)點(diǎn)上 {f2(b),…fr(b)}。 為保證MDS性質(zhì)，第一個(gè)校驗(yàn)節(jié)點(diǎn)中的數(shù)據(jù)不作修改。首先利用第一子條帶的數(shù)據(jù)分塊情況S， 將前r-1份數(shù)據(jù)Si,(i=1,…,r-1) 與第二子條帶中的后r-1 個(gè)校驗(yàn)節(jié)點(diǎn)數(shù)據(jù)進(jìn)行異或操作，更新保存到校驗(yàn)節(jié)點(diǎn)中。然后將第r份數(shù)據(jù)Sr通過橫向減法原則間接保存在第一子條帶中的第二個(gè)校驗(yàn)節(jié)點(diǎn)中，即第一子條帶的第二個(gè)校驗(yàn)節(jié)點(diǎn)的數(shù)據(jù)減去同一節(jié)點(diǎn)的第二子條帶數(shù)據(jù)。

以O(shè)Hitchhiker碼 (n=13,k=10) 為例，編碼結(jié)構(gòu)如圖2所示。

圖2 OHitchhiker碼 (n=13,k=10) 的編碼結(jié)構(gòu)

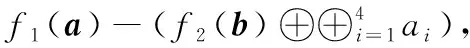
2.3 OHitchhiker修復(fù)過程

當(dāng)節(jié)點(diǎn)失效時(shí)，通過下載一定數(shù)據(jù)塊，利用MDS性質(zhì)計(jì)算恢復(fù)出節(jié)點(diǎn)數(shù)據(jù)，將失效的塊重新寫入，這個(gè)過程被稱為數(shù)據(jù)修復(fù)。OHitchhiker碼最多能容忍r個(gè)節(jié)點(diǎn)失效，而在分布式存儲(chǔ)系統(tǒng)中單節(jié)點(diǎn)失效占比高達(dá)90%，所以本文主要討論單節(jié)點(diǎn)失效而啟動(dòng)修復(fù)的過程。

OHitchhiker碼的修復(fù)過程分成如下4步：假設(shè)節(jié)點(diǎn)Nodei失效，即數(shù)據(jù)ai,bi失效。

(1)下載第二子條帶中的數(shù)據(jù){b1,…,bk,f1(b)}/bi， 共k個(gè)數(shù)據(jù)，據(jù)MDS性質(zhì)，計(jì)算恢復(fù)出原數(shù)據(jù)bi。

(2)通過動(dòng)態(tài)選擇數(shù)據(jù)分配算法DSDA生成分塊情況S， 判斷節(jié)點(diǎn)Nodei中ai屬于Sj,(j=1,…,r-1) 還是Sr。

(3)如果數(shù)據(jù)ai∈Sj,(j=1,…,r-1)， 即存放在第二個(gè)子條帶的校驗(yàn)節(jié)點(diǎn)中。那么首先下載含有數(shù)據(jù)ai的校驗(yàn)塊 [f2(b)⊕Sj]， 因?yàn)榇藭r(shí)b已經(jīng)全都下載，那么線性組合f2(b) 也就得到；再下載{Sj}/ai， 共|Sj|-1個(gè)數(shù)據(jù)，相互異或恢復(fù)出數(shù)據(jù)ai； 此時(shí)共下載 |Sj| 個(gè)數(shù)據(jù)。

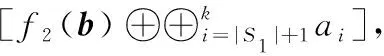
以O(shè)Hitchhiker碼 (n=13,k=10) 為例，當(dāng)節(jié)點(diǎn)Node8失效時(shí)，修復(fù)過程如圖3所示。

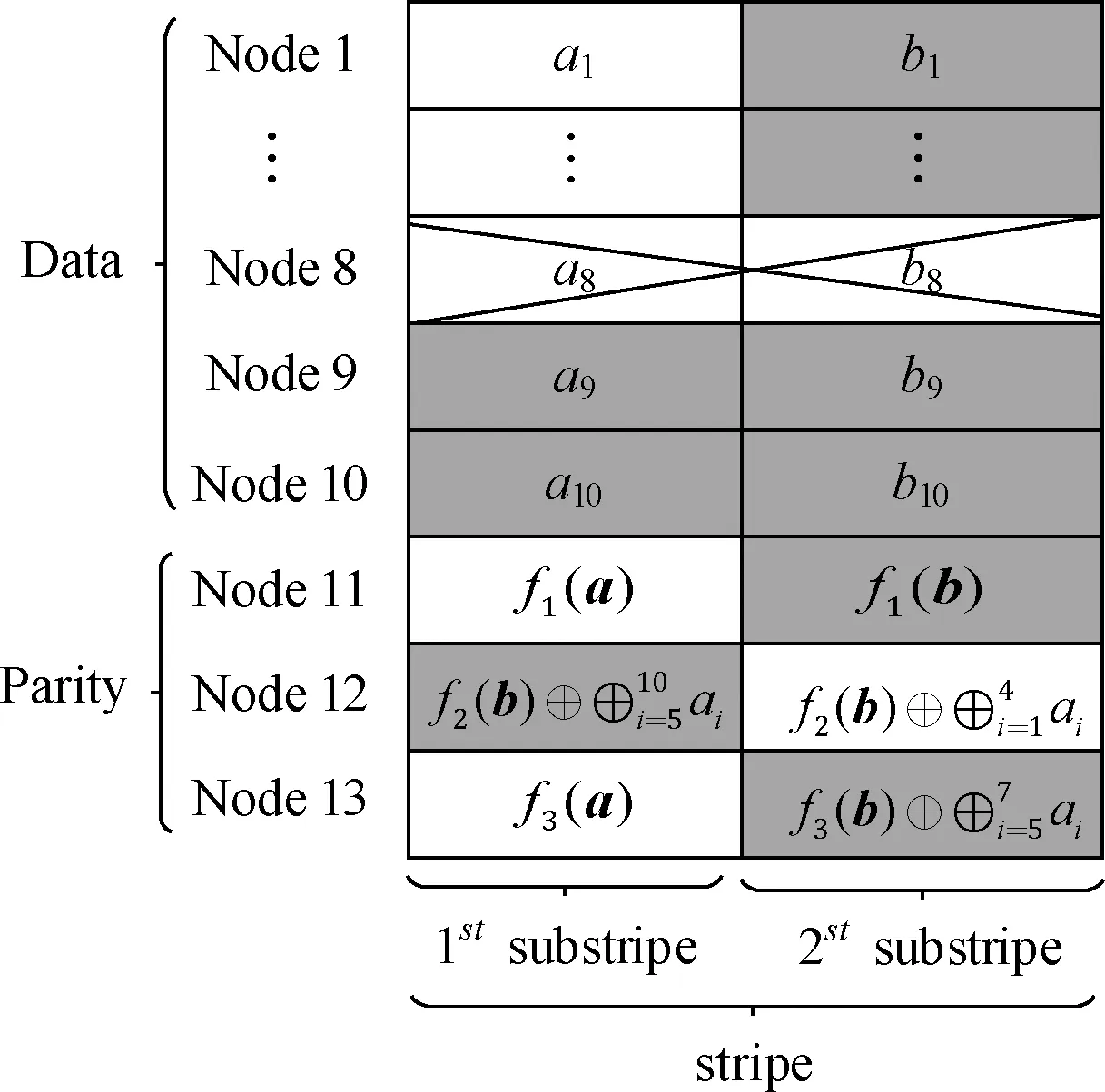
圖3 OHitchhiker碼 (n=13,k=10) 的節(jié)點(diǎn)修復(fù)

3 實(shí)驗(yàn)結(jié)果與分析

本文在HDFS-RAID[14]中實(shí)現(xiàn)OHitchhiker碼，通過插件方式將編碼加入HDFS中，此時(shí)的分布式容錯(cuò)存儲(chǔ)系統(tǒng)稱為HDFS-OHitchhiker。根據(jù)實(shí)驗(yàn)結(jié)果，對(duì)比分析OHitchhiker碼與RS碼、Hitchhiker-XOR碼和Hitchhiker-XOR+碼的平均修復(fù)帶寬、修復(fù)帶寬率和總修復(fù)下載量。

3.1 實(shí)驗(yàn)環(huán)境

實(shí)驗(yàn)通過部署分布式系統(tǒng)集群，集群由一個(gè)NameNode節(jié)點(diǎn)和19個(gè)DateNode節(jié)點(diǎn)組成。所有節(jié)點(diǎn)運(yùn)行在Ubuntu16.04系統(tǒng)和JDK1.7.0_37中，其中每個(gè)節(jié)點(diǎn)配置兩個(gè)8核Intel 2.5 GHz處理器，48 G RAM，2T硬盤和 2 GB/s 以太網(wǎng)卡。

實(shí)驗(yàn)數(shù)據(jù)為500個(gè)640M文件，保持默認(rèn)HDFS的數(shù)據(jù)塊大小64 M，通過設(shè)置不同 (n,k) 參數(shù)和4種編碼策略(OHitchhiker碼、RS碼、Hitchhiker-XOR碼和Hitchhiker-XOR+碼)，將每個(gè)文件分塊編碼分布式存儲(chǔ)在DataNode節(jié)點(diǎn)中。

3.2 實(shí)驗(yàn)分析

3.2.1 平均修復(fù)帶寬

為了更全面的比較，我們通過實(shí)驗(yàn)計(jì)算并對(duì)比了滿足k∈{1,…,100},n∈{k+1,…,2k} 的所有取值下4種編碼的實(shí)際平均修復(fù)帶寬，發(fā)現(xiàn)OHitchhiker碼在所有 (n,k) 參數(shù)情況下都是最優(yōu)的。

表2 系統(tǒng)節(jié)點(diǎn)平均修復(fù)帶寬對(duì)比

3.2.2 修復(fù)帶寬率

當(dāng)系統(tǒng)節(jié)點(diǎn)失效時(shí)，修復(fù)節(jié)點(diǎn)下載量占原數(shù)據(jù)總量的百分比，稱為修復(fù)帶寬率rsys

(4)

圖4描述在 (n,k)={(8,5),(9,6),(12,8)} 這3種取值下，Hitchhiker-XOR，Hitchhiker-XOR+和OHitchhiker碼之間的系統(tǒng)節(jié)點(diǎn)修復(fù)率對(duì)比圖，圖中的橫坐標(biāo)表示參數(shù) (n,k)， 縱坐標(biāo)表示系統(tǒng)節(jié)點(diǎn)的修復(fù)帶寬率。

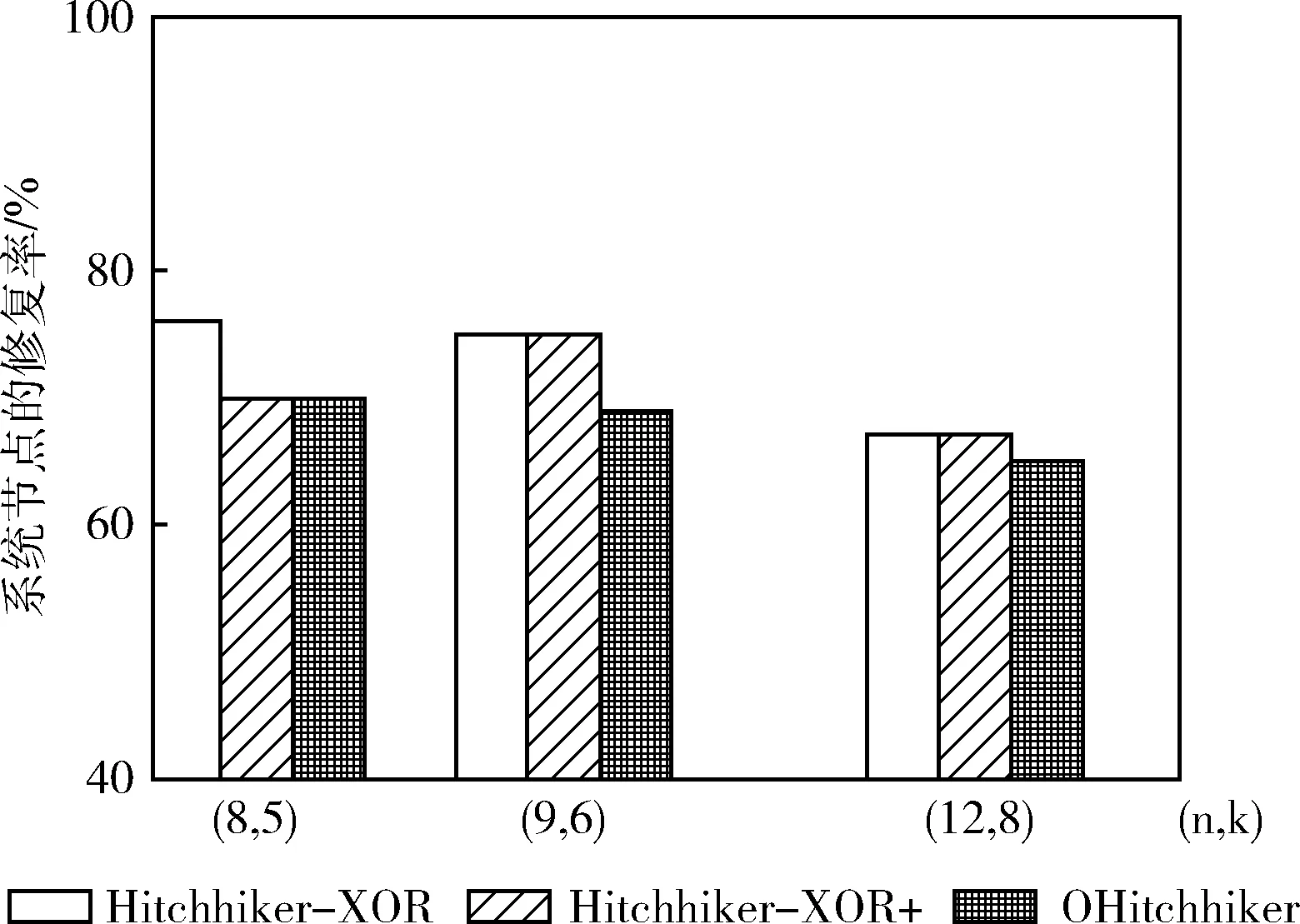
圖4 Hitchhiker和OHitchhiker碼的修復(fù)率對(duì)比

從圖4中可以發(fā)現(xiàn)，OHitchhiker碼的系統(tǒng)節(jié)點(diǎn)修復(fù)率始終保持最低。在參數(shù)為 (n,k)=(8,5) 時(shí)，OHitchhiker碼的修復(fù)帶寬率相比于Hitchhiker-XOR碼降低了6%，與Hitchhiker-XOR碼則相同。在參數(shù)為 (n,k)=(9,6) 時(shí)，OHitchhiker碼的修復(fù)帶寬率相比于Hitchhiker-XOR碼和Hitchhiker-XOR+碼都降低了5.6%。在參數(shù)為 (n,k)=(12,8) 時(shí)，OHitchhiker碼的修復(fù)帶寬率相比于Hitchhiker-XOR和Hitchhiker-XOR+碼都降低1.6%。

3.2.3 總修復(fù)下載量

修復(fù)每個(gè)系統(tǒng)節(jié)點(diǎn)所需的下載量之和，稱為總修復(fù)下載量δsys

(5)

圖5(a)描述在保持總節(jié)點(diǎn)數(shù) (n=12) 不變的情況下，隨著校驗(yàn)節(jié)點(diǎn)數(shù) (r=1,…,6) 增加，RS碼、Hitchhi-ker-XOR碼、Hitchhiker-XOR+碼和OHitchhiker碼之間的下載量對(duì)比折線圖。圖中橫坐標(biāo)表示校驗(yàn)節(jié)點(diǎn)數(shù)，縱坐標(biāo)表示系統(tǒng)節(jié)點(diǎn)總修復(fù)下載量。

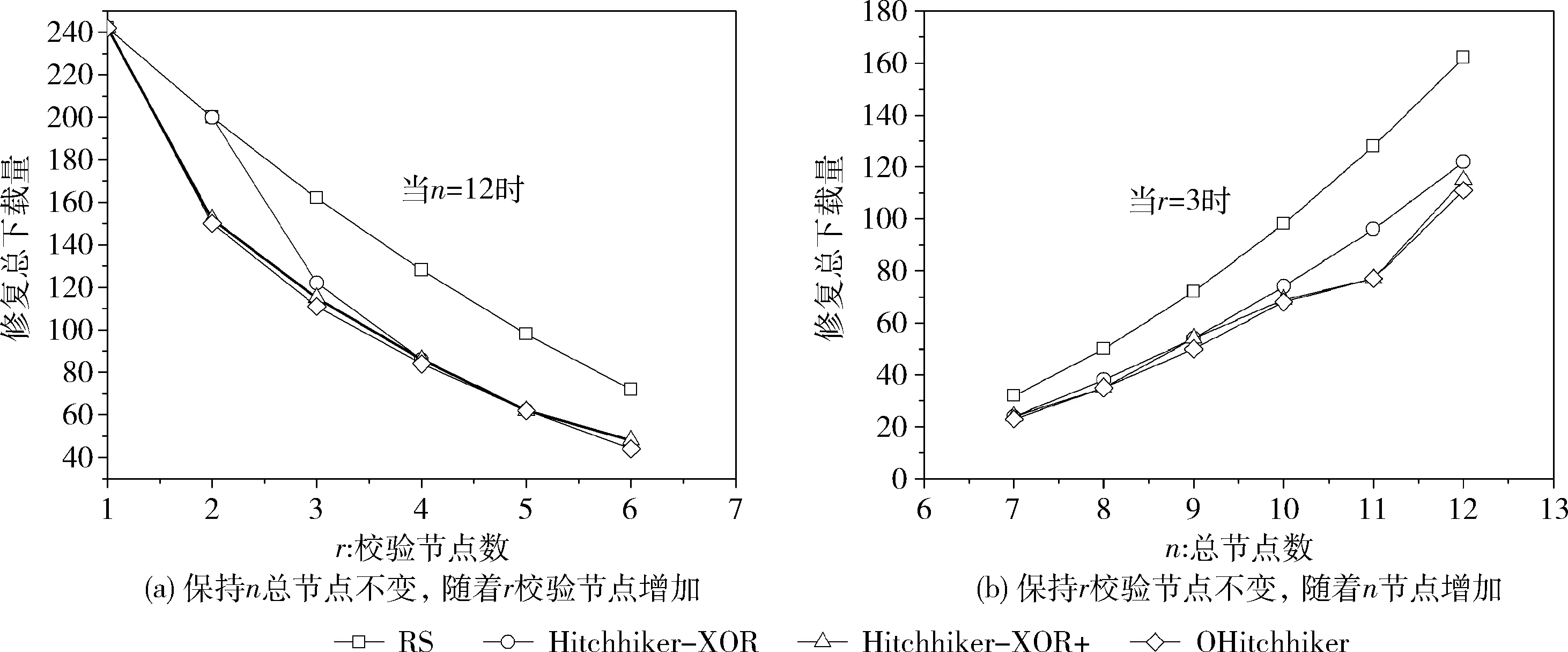
圖5 RS、Hitchhiker和OHitchhiker碼的總修復(fù)下載量對(duì)比

圖5(b)描述在保持校驗(yàn)節(jié)點(diǎn)數(shù) (r=3) 不變的情況下，隨著總節(jié)點(diǎn)數(shù) (n=7,…,12) 增加，RS碼、Hitchhiker-XOR碼、Hitchhiker-XOR+碼和OHitchhiker碼之間的下載量對(duì)比折線圖。圖中橫坐標(biāo)表示總節(jié)點(diǎn)數(shù)，縱坐標(biāo)表示系統(tǒng)節(jié)點(diǎn)總修復(fù)下載量。

從圖5中可發(fā)現(xiàn)，隨著r的增加，RS碼、Hitchhiker-XOR碼、Hitchhiker-XOR+碼和OHitchhiker碼的修復(fù)下載量整體減少；隨著n的增加，RS碼、Hitchhiker-XOR碼、Hitchhiker-XOR+碼和OHitchhiker碼的修復(fù)下載量整體增加。所以不管是總節(jié)點(diǎn)還是校驗(yàn)節(jié)點(diǎn)怎樣變化，相比于RS碼、Hitchhiker-XOR碼和Hitchhiker-XOR+碼，OHitchhiker碼的總修復(fù)下載量始終保持最低。

4 結(jié)束語

本文通過研究分布式存儲(chǔ)系統(tǒng)的Hitchhiker碼，在分析均分?jǐn)?shù)據(jù)分配算法的基礎(chǔ)上，提出一種最優(yōu)分配的OHitchhiker碼。它可針對(duì)不同 (n,k) 值動(dòng)態(tài)選擇最優(yōu)的數(shù)據(jù)分配算法，利用DSDA算法使得編碼結(jié)構(gòu)具有最小修復(fù)帶寬，進(jìn)一步降低修復(fù)成本。理論分析及實(shí)驗(yàn)結(jié)果表明，在任意 (n,k) 參數(shù)取值下，對(duì)比RS碼和Hitchhiker碼，OHitchhiker碼始終保持最低修復(fù)下載帶寬。

但是本文基于Pigyybacking框架下設(shè)計(jì)的OHitchhiker碼，只降低了系統(tǒng)節(jié)點(diǎn)失效時(shí)的修復(fù)下載帶寬；當(dāng)校驗(yàn)節(jié)點(diǎn)失效時(shí)，仍根據(jù)MDS性質(zhì)下載任意k個(gè)數(shù)據(jù)進(jìn)行修復(fù)，沒有進(jìn)行任何改進(jìn)。下一步工作將關(guān)注校驗(yàn)節(jié)點(diǎn)的修復(fù)過程，進(jìn)一步減少校驗(yàn)節(jié)點(diǎn)的修復(fù)下載帶寬。