基于氣象要素內插的地基GPS/PWV方法研究與精度分析

申建華

(上海市測繪院,上海 200063)

0 引 言

水汽作為大氣的重要組成部分,在空間中有著極不均勻的分布,同時它的細微變化足以影響著整個大氣環境,也是產生災難性天氣環節中的重要影響因子,如何精準分析水汽的分布及狀態變化是當前氣象學及天氣預報重點研究的方向[1-2]．GPS氣象學是集合了高精度、高時空分辨率、近實時等優點的非常具有應用前景的新一代大氣遙感技術學科之一[3-5]．在突發氣象災害預警[6]、監測大氣狀態[7]等方面被規模化應用．Bevis等人[8-9]在20世紀90年代提出利用GPS反演站點天頂方向大氣可降水汽量(PWV)的實驗,實現了利用GPS觀測PWV的設想,在氣象學中此項技術逐步得到了較高的關注[10],此后NIELL利用氣象專業技術手段比較分析出GPS反演的水汽精度可達到1 mm[11]．

近些年來隨著理論與技術的發展,GPS水汽反演也逐步在實際應用中嶄露頭角．Musal對GPS解算得到的PWV數據進行了分析,得出探空數據相關系數高于0.85,兩者之間存在極強的相關性[12]．Shoji[13]利用日本境內所有的GPS氣象站點,給出兩種可以體現對流層水汽局部變化的優于PWV的水汽指數,同時指出其在雷暴監測方面的可行性．楊嬌等[14]利用2010年香港地區地基GPS水汽數據和MODIS近紅外水汽數據,提出了一種基于地基GPS訂正MODIS水汽產品繼而得到高精度空間連續分布PWV的方法,修正結果較好．范士杰等[15]對GPS水汽反演的雙向濾波結果進行了分析,得出精密單點定位(PPP)雙向濾波可以克服單向濾波初期的水汽收斂問題,且雙向濾波PWV結果明顯優于單向濾波．我國的北斗衛星導航系統(BDS)在近些年得到了長足發展,郭巍[16]、施闖等[17]基于BDS進行了水汽反演結果分析,與GPS相比雖存在2～3.3 mm的系統誤差,但與探空數據有著很好的一致性．在三維水汽層析方面,王維等[18]對長三角地區進行了多模全球衛星導航系統(GNSS)水汽層析仿真實驗,改善了層析結果．姚宜斌等[19]提出一種附加虛擬傾斜路徑信號精化水汽層析模型的方法,使層析結果更加逼近真值．

當利用地基GPS獲取水汽數值時,站點氣壓和溫度也需要同時獲取得到．精確獲取的基站大氣壓強參數,可根據相應的數學模型解算得到精確的干延遲數據,進而根據干濕延遲關系分離得到準確的天頂濕延遲數據[20]．為提高天頂濕延遲到PWV的換算精度,需要獲得準確的站點溫度[21]．而我國地域遼闊,社會經濟發展差異較大,無法保證每一個地區的GPS站點都能擁有符合規范的氣象要素觀測儀器．怎樣準確實時獲取站點的氣象參數,是當前地基GPS氣象站網規劃的亟待解決的問題．

本文以2016年夏季獲取的GPS氣象文件(M文件)為原始數據.對于無法獲取氣象參數的站點,利用增加高度修正的反距離加權內插法.在全國范圍內以省為單位選擇25處試驗站點,對參數結果進行精度分析．同時將試驗氣象參數引入GPS水汽反演,分析解算結果精度,以確定此方法能否應用于實際的地基GPS反演水汽．

1 引入高度修正后的反距離加權

1.1 引入高度修正的氣壓值

海拔高度是大氣壓強的重要影響因素之一,海拔高度的變化會對氣壓產生如下影響[22]:

ΔP=P1(e-0.03415Δh/T1-1),

(1)

式中:ΔP為目標站點氣壓引入高度差后的修正值,hPa;P1為基礎站點的氣壓值,hPa;T1為基礎站點溫度值,K;Δh為測站間海拔高度差,m．

1.2 引入高度修正的溫度值

ΔT=Δh×0.0065,

(2)

式中,ΔT是目標站點引入高度差后的修正數值,K．

1.3 反距離加權原理

反距離加權是根據相近相似的原理,權重大小與基礎站點和目標站點之間的距離呈反比關系[23]．基本方法如下:

{P=∑ωi(Pi+ΔPi),

T=∑ωi(Ti+ΔTi).

(3)

式中:ΔPi、ΔTi分別為第i個基礎站的氣壓和溫度引入高度后的修正值;Pi、Ti為第i個基礎站的氣壓和溫度；ωi是權函數:

ωi=h-μi/∑nj=1h-μj)，

(4)

式中:μ=2;hi為目標站點至基礎站點的距離;n為參與內插的站點總數．

2 內插精度實例分析

2.1 實驗源數據選擇

在全國范圍內綜合考慮各省基站的分布情況及地形特征,選擇了具有代表性的25個目標站點,如圖1所示,圓圈為內插半徑范圍,圈內的點為目標站點與內插站點．其中部分省份由于站點分布較少如寧夏、海南等,因此沒有安排目標站點,在站點相對密集的省(市)份如北京、江蘇,則多安排了一個目標站點．將年積日153-244,采樣間隔為1 h的GPS站點氣象觀測文件集進行整理,單個站點的樣本容量約為2 208個．收集目標站點附近10～300 km具有氣象觀測文件的站點作為基礎站點,通過內插得到目標站點氣象參數．表1示出了實驗站點編碼、站點高程和內插半徑．

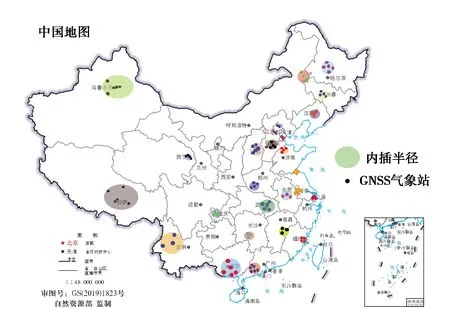
圖1 實驗站點分布圖(圓圈表示內插半徑)

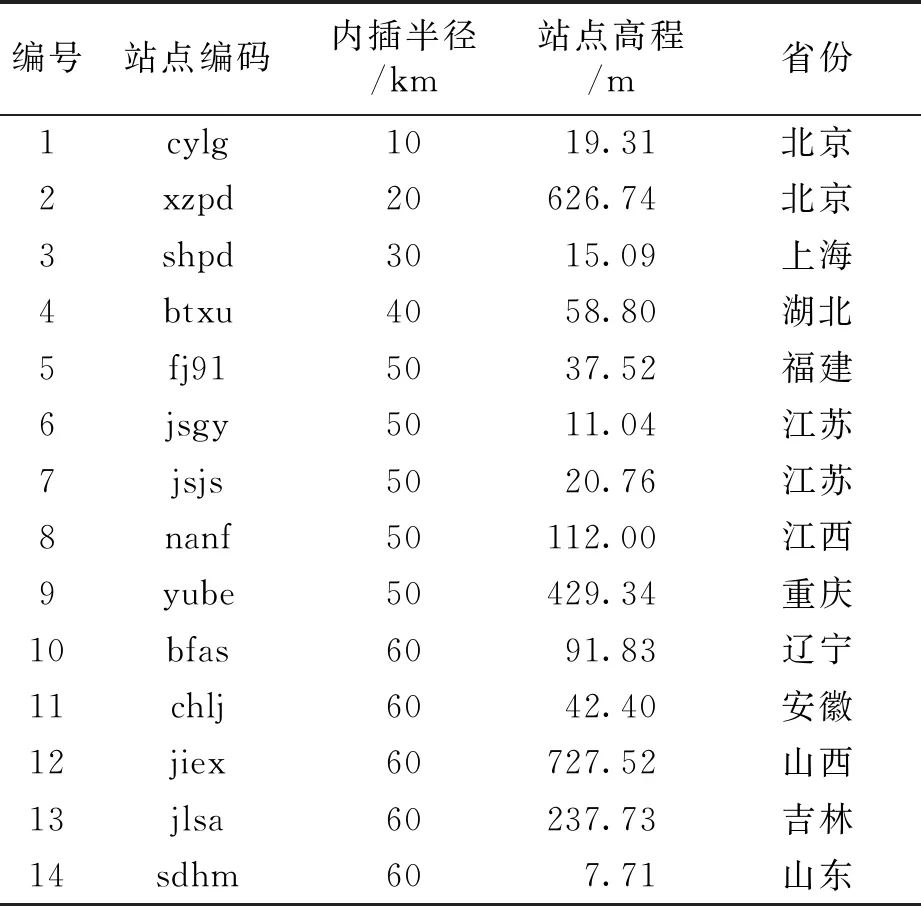
表1 實驗站點高程與內插半徑

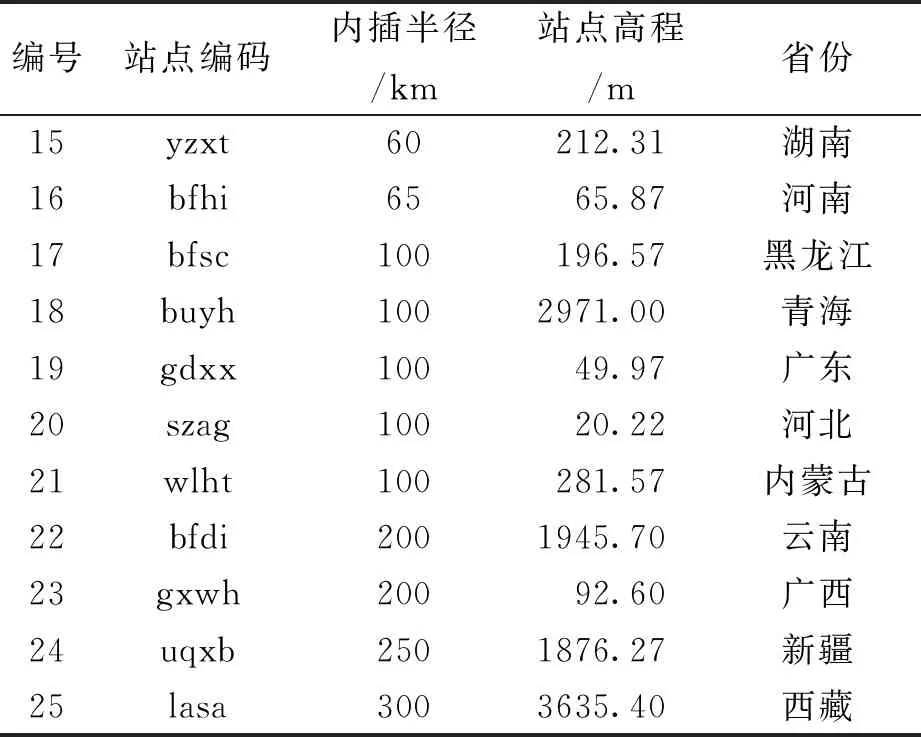
表1(續)

2.2 實驗結果分析

基于本文所提方法,對25個實驗目標站點氣象參數進行計算,獲得目標站點的內插值,將之與目標站點實測值進行比較．統計實驗結果的平均偏差、相關系數及均方差如表2所示．從表2可以得出,利用本文方法內插獲得的各目標站點溫度及氣壓實驗值與真實值的均方差及平均偏差都較小,且具有極強的相關性,可初步判斷本文計算獲得的氣象參數可信度較高．

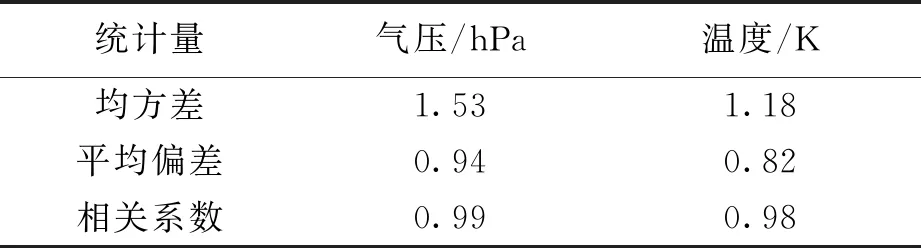
表2 25個目標站點的統計結果

1)所在區域差異

根據所選實驗區域分布特征,將25個目標站點按照東、中、西部區域劃分,其中東部區域有10個站點,中部區域有9個站點,西部區域有6個站點．對各區域氣壓和溫度的均方根誤差(RMS)進行分析,表3示出了統計結果．

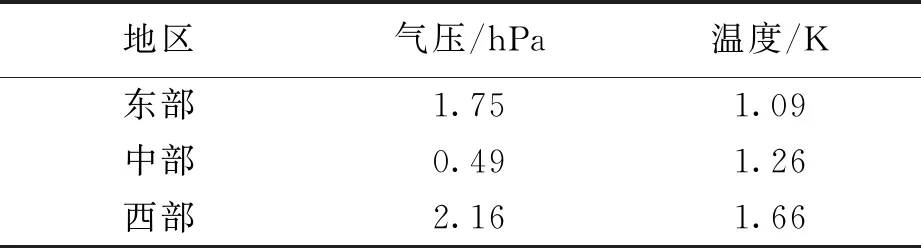
表3 東、中、西部內插結果的均方差

從表3可以看出,在氣壓數據上,中部區域數據計算結果遠優于東西部結果,中部RMS較東部低1.26 hPa,較西部低1.67 hPa;在溫度數據上,東部數據計算結果略優于中部及西部,差距僅在0.5 K左右．

2)實驗區域所處海拔高度的影響

將目標站點海拔高度按由高到低排序,分別計算氣壓與溫度的殘差序列,如圖2所示.

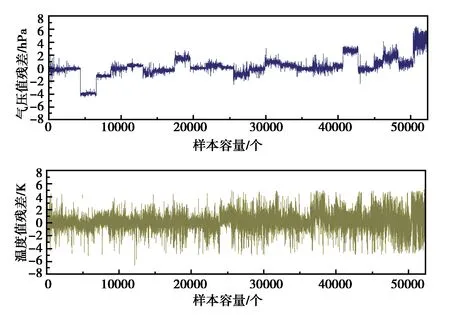
圖2 整體氣象要素的殘差序列

從圖2中可以看出,溫度及氣壓殘差值隨著目標站點所處海拔高度的上升均呈增大趨勢,氣壓殘差有明顯的站點集中性,即同一個站點的氣壓殘差大小幾乎相等,不同站點的氣壓殘差差別較大．而溫度殘差則在0刻度線附近上下波動,呈正態分布．

3)內插實驗區域分布半徑影響

將各目標站點按內插半徑從小到大排列，分析各站點的氣壓與溫度RMS如圖3所示．從圖中可以看出溫度的RMS隨著內插半徑的增加而增加,除個別站點外氣壓的RMS,變化趨勢與溫度相似．從整體來看溫度殘差的RMS雖然整體較為均勻,主要分布在0～1.5 K,但多數要高于氣壓殘差RMS．氣壓殘差RMS基本低于1 hPa．但是個別站點RMS出現跳躍情況,這說明對于某些特殊站點,氣壓內插的效果會存在一定的偶然誤差．

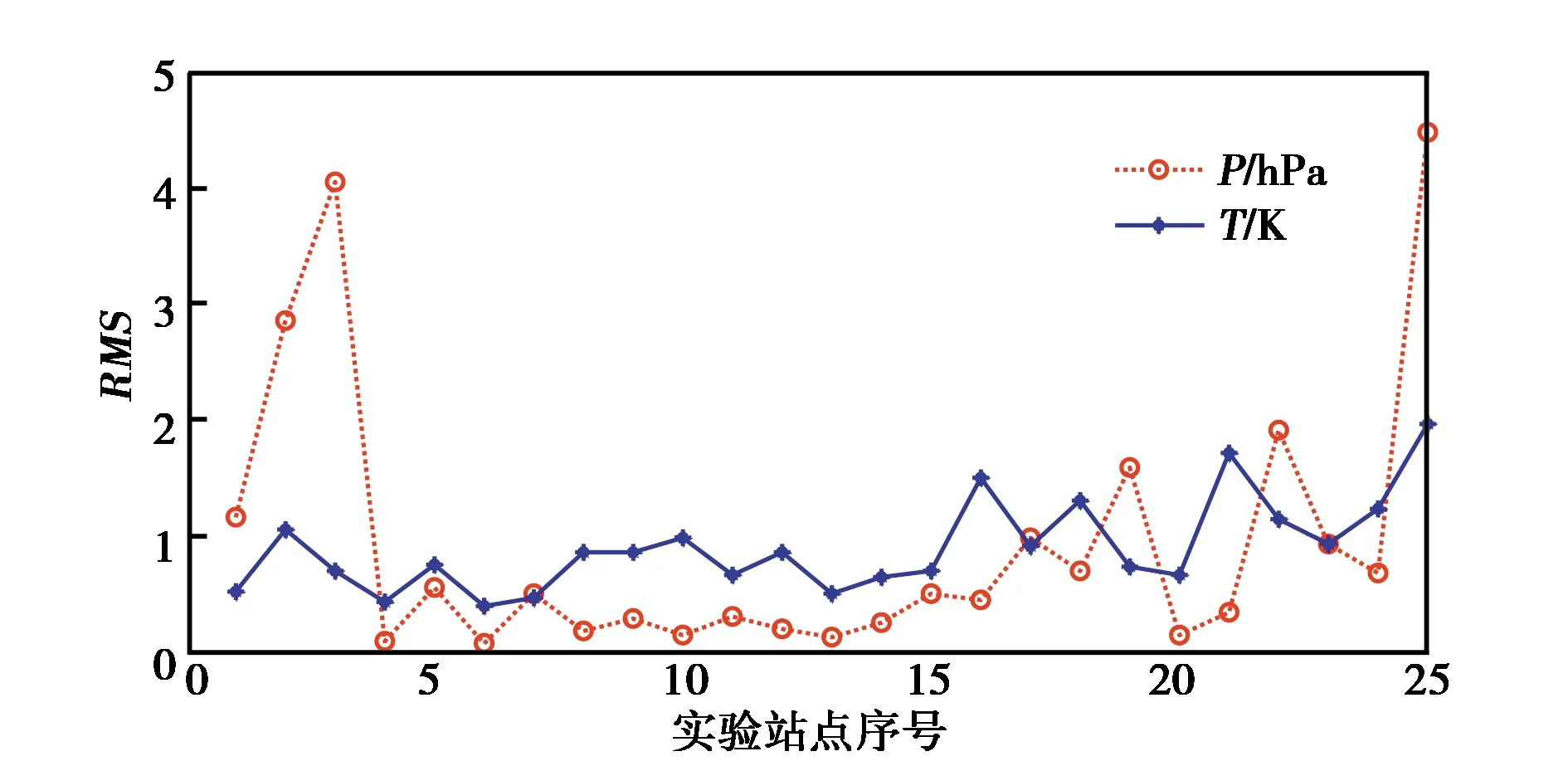
圖3 氣壓、溫度RMS序列(內插半徑越來越大)

綜合以上各組數據來看,本文所提方法獲得的氣壓、溫度數據可信度較高,同時精度也受到地理區域、海拔高度及站間距離的影響．同時，基于本文所提增加高度修正的反距離加權法計算得到的氣象參數，可以滿足GPS水汽解算精度需求．

3 基于本文方法內插結果對GPS水汽解算的影響

為驗證本文計算得到氣象參數是否對地基GPS水汽解算精度有顯著的影響,下面基于高精度數據后處理軟件 GAMIT/GLOBK,將均勻分布在我國周圍的國際GNSS服務(IGS)站(TSKB IISC POL2 GUAM KIT3)作為參考站點,對本文所選取的25個目標站點對應時段的GPS觀測數據進行批量化處理,獲得各目標站點逐小時PWV序列．將本文計算的氣象參數解算得到的水汽值為目標PWV,利用真實氣象參數解算得到的水汽值為真實PWV,將PWV兩者值進行比較分析,即可驗證實驗結果是否對GPS水汽解算精度有顯著影響,如圖4所示．同時為進一步分析氣象參數對水汽解算結果的影響區別,將實驗氣象參數與真實氣象參數相互置換,分別將單獨利用溫度和氣壓內插計算的水汽值記為T-PWV及P-PWV,統計各實驗結果與真實PWV間的數值關系,如表4所示．

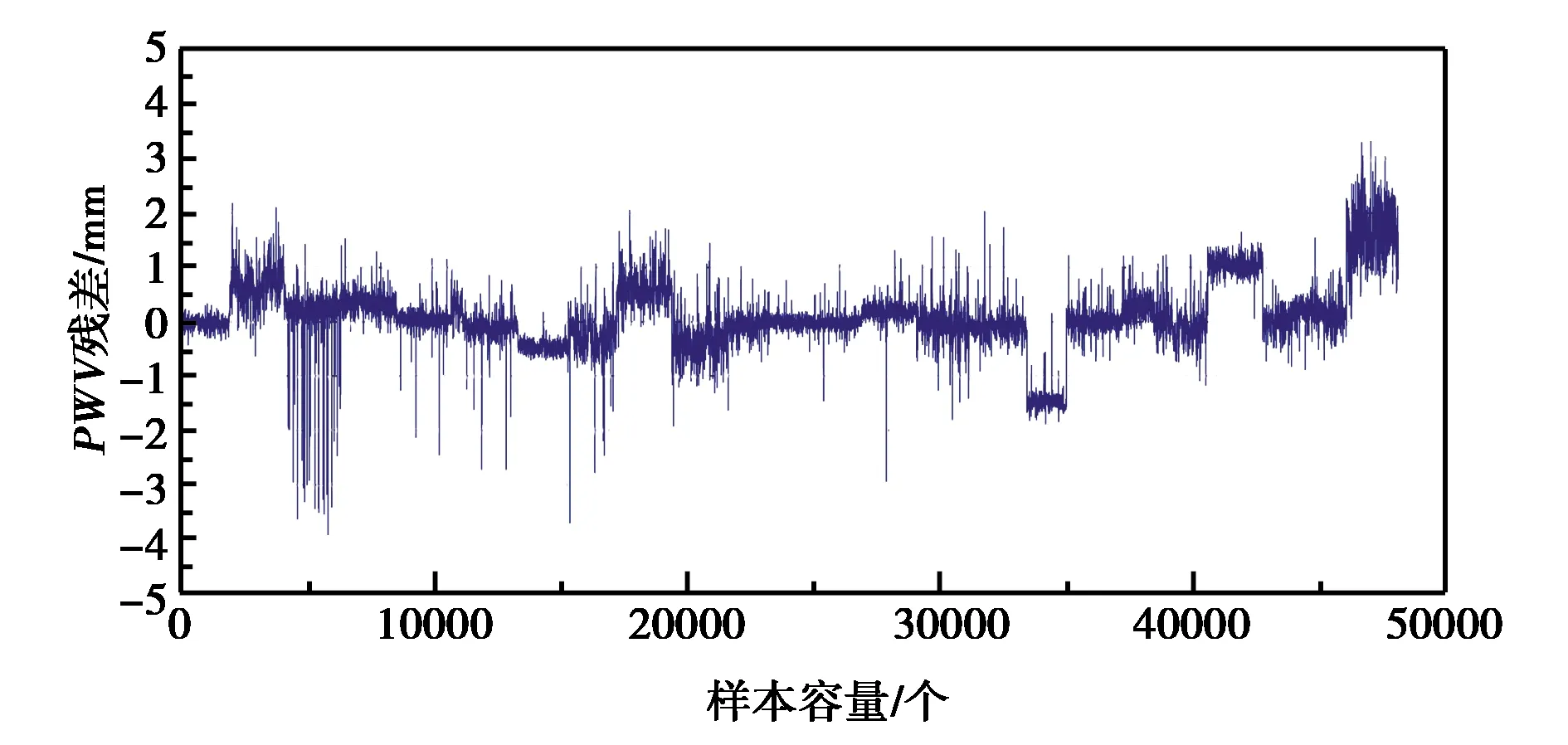
圖4 內插PWV和實測PWV的殘差

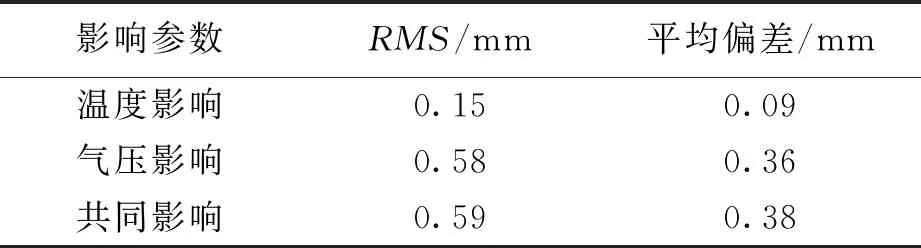
表4 內插PWV的統計結果

從圖4可以看到,在25個目標站點共有48 000份實測PWV與內插PWV殘差值樣本,數值均分布在0 mm上下,其中分布在-1～1 mm的殘差值約占樣本總量的89%.從表4中可以看到,二者的平均偏差及RMS分別為0.38 mm和0.59 mm,且高于單氣壓影響和單溫度影響,單溫度內插得到的PWV的RMS比單氣壓內插得到的RMS小0.43 mm,平均偏差要小0.27,因此，水汽解算的精度主要受氣壓內插精度的影響．

如圖5所示,25個實驗站點中,有22個站點的PWVRMS和平均偏差都小于1 mm，另3個站點的PWVRMS和平均偏差為1.5 mm左右．如圖6所示為這三個站點的內插PWV與實測PWV的對比．兩者的結果相差很小．

綜上,內插氣象要素對水汽解算的精度沒有顯著影響,本文所用方法能夠滿足GPS水汽解算的精度要求．

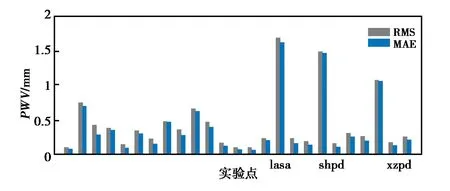
圖5 25個目標站點的內插PWV的RMS與平均偏差直方圖

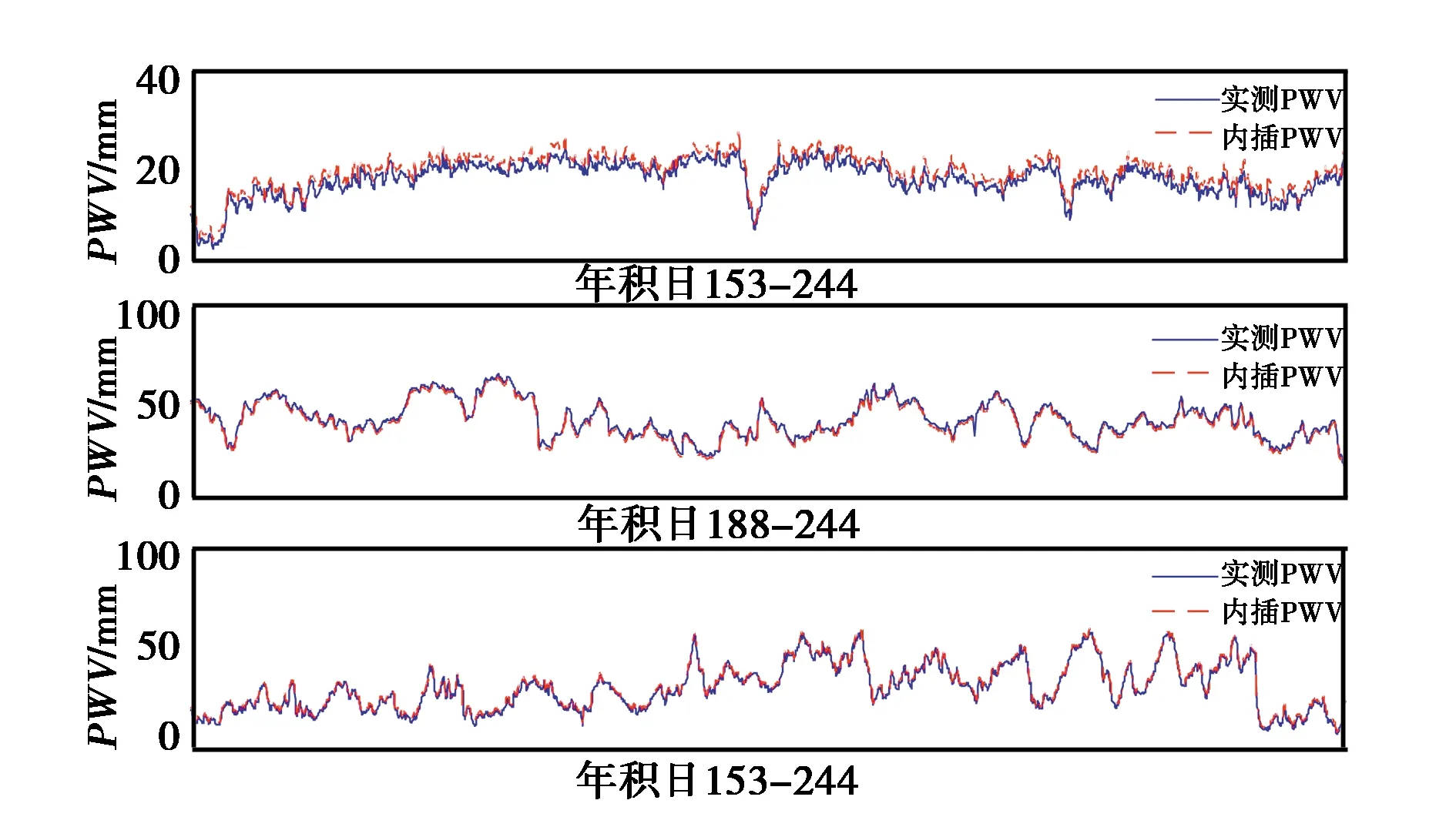
圖6 lasa、shpd和xzpd三個站點的PWV對比

4 本文方法與溫壓模型GPT2得到的水汽結果精度分析

GPT2模型是對全球氣溫和氣壓經驗模型(GPT)的優化,在GPS數據解算中常被用作氣象參數的計算,也在GPS水汽反演中有較多的應用[24]．本文將基于香港地區的觀測數據對本文方法計算得到的水汽值同基于GPT2模型計算得到水汽值進行精度比較．

選擇HKOH、HKWS、HKSL、HKSC四個具有不同地形特征的香港連續運行參考站(CORS)作為實驗站點,收集2019年年積日192-201共9天的觀測數據及氣象數據、實驗站點10 km之外的其它站點的氣象文件．建立三個實驗方案對結果進行對比分析．實驗方案一：將實驗站點實際觀測得到的氣象文件參與水汽解算結果記為PWV,并視為真值;實驗方案二：將基于GPT2模型計算得到氣象參數參與到水汽解算并將結果記為G-PWV;實驗方案三：將利用本文方法計算得到氣象參數參與到水汽解算,并將結果記為TP-PWV;圖7是不同實驗方案的各站點水汽計算結果折線圖,表5所示為二、三種方案的平均偏差及RMS．

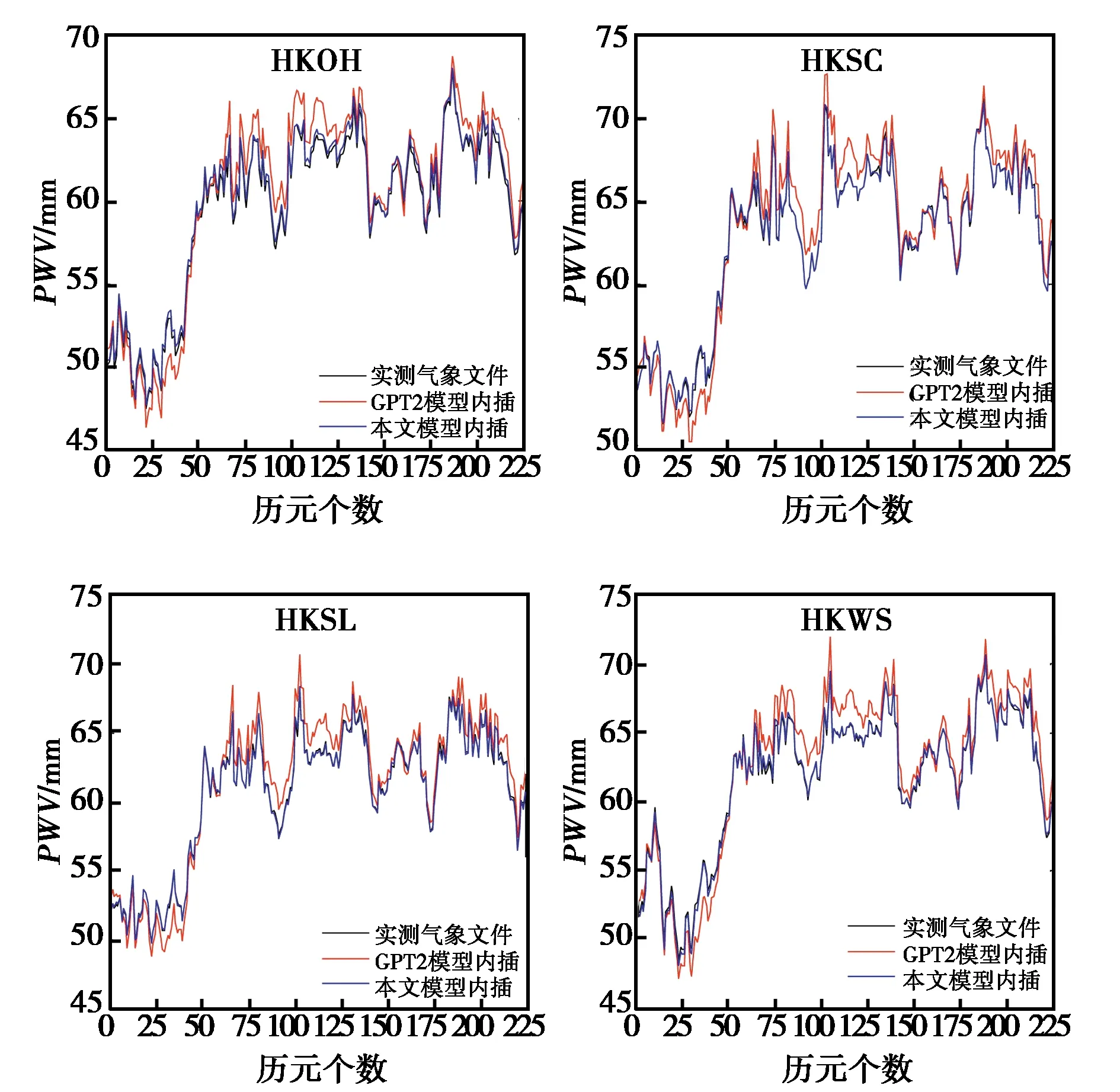
圖7 各站在不同實驗方案下解算結果

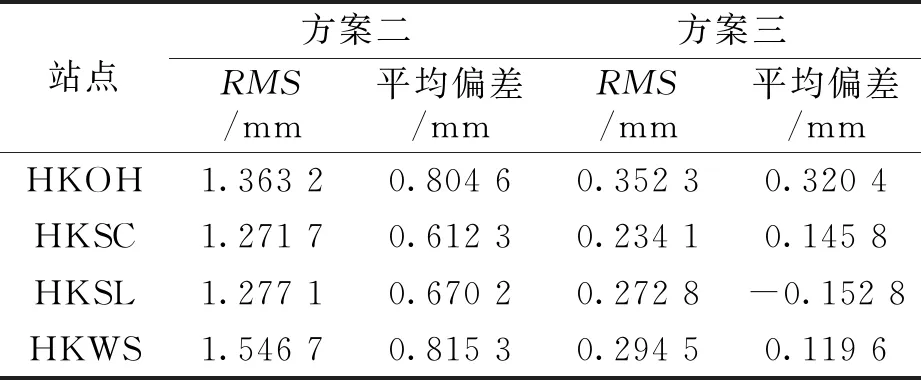
表5 二、三方案平均偏差與誤差

從圖7中可以看出各站點各方案計算的水汽值變化趨勢基本相同,但在一、二號方案間始終存在±2 mm的差值,而一、三方案基本一致．從表5中可以看到,二號實驗方案的RMS均在1.1 mm以上,平均偏差高于0.5 mm．三號方案除在HKOH站點處平均偏差為0.320 4 mm差值之外,其余站點均在0.2 mm之下,除HKOH站點的RMS為0.352 3 mm之外,其余均在0.3 mm以內．因此實驗表明,相對準確的氣象參數有利于提高地基GPS水汽反演精度,且在香港地區本文所提出方法在計算地面氣象參數精度方面優于GPT2模型．

5 結 論

準確地獲取站點氣象數據，是影響地基GPS水汽解算精度重要因素之一,但相當部分GPS連續運行站點受建設時條件限制,未能安裝相應的氣象傳感器件．針對這一問題，本文提出了增加高度修正的反距離加權法內插來獲取觀測站點的氣象數據,并在全國觀測站點中選擇了25個作為實驗站點,將距實驗站點一定范圍的基礎站點的氣象要素內插到了實驗站點．并將其在GPS水汽解算中應用,得到以下結論:

1)利用本文方法得到的氣象數據與實際獲取的氣象數據相關性極強,氣壓及溫度的RMS分別為1.53 hPa和1.18 K,所以通過本文方法解算的氣象數據精度可靠性較高．

2)所有試驗站點的氣象數據精度都較高,綜合分析發現中部精度高于東部和西部,同時內插精度也隨著海拔高度和內插半徑的改變而改變,但影響并不顯著．

3)在地基GPS水汽解算實驗中,加入本文方法得到的氣象數據解算的PWVRMS為0.59 mm，平均偏差為0.38 mm，因而通過本文方法計算得到的氣象數據可滿足實際水汽解算精度要求．

4)對香港地區實驗站點數據分析表明，基于本文所提方法計算的地面氣象參數精度優于GPT2模型．