MADOCA-LEX高頻GPS衛星鐘差短期預測精度分析

虢盛,張紹成,李瑋,獨士康

(中國地質大學(武漢) 地理與信息工程學院,湖北 武漢 430078)

關鍵字: 全球定位系統;衛星鐘差;阿倫方差;穩定性分析;鐘差預報

0 引 言

衛星鐘的穩定性是影響全球衛星導航系統(GNSS)導航定位精度的重要因素[1]．國際GNSS服務組織(IGS)提供采樣率為30 s和5 min的GPS精密鐘差,但其較低的采樣頻率和產品時延無法滿足實時高頻高精度用戶的需求[2]．日本準天頂衛星系統(QZSS)作為一個區域性衛星導航系統,除播發與GNSS相同的導航定位信號外,還通過衛星頻段播發采樣率為1 s的精密鐘差和采樣率為30 s的精密軌道產品[3],使得能夠消除在分析衛星鐘穩定性時使用較低頻采樣率數據內插高頻數據引起的粗差[4]．日本宇宙航空研究開發機構(JAXA)提供的精密軌道和鐘差產品是MADOCA (Multi-GNSS Advanced Demonstration tool for Orbit and Clock Analysis)數據處理軟件生成,并通過L頻段1278.75 MHz的實驗頻率播發給地面用戶,因而也被稱為MADOCA-LEX(L-band Experiment)產品[5]．

國內外學者已就GNSS衛星鐘差的中長期穩定性和預報技術進行了較多的研究：文獻[6]基于IGS提供的采樣率為30 s的鐘差產品對衛星鐘的中長期穩定性進行了分析[6],文獻[7]采用灰色模型對6 h的鐘差進行了中長期預報和最優預報模型的探究[7]．這些研究主要針對衛星鐘在與地面監測站失聯后,僅靠自身維持與系統時間同步時所做的中長期預報,文獻[8-9]揭示了其普遍精度一般在納秒級別,主要用于數米精度的導航應用．JAXA發布的MADOCA-LEX產品提供了0.1 ns精度的鐘差,但實時播發中可能存在6～8 s的時延[5],在用戶使用過程中鐘差對測距精度的影響會進一步增加．因此需要分析衛星鐘差在數秒內的短期穩定性,評估實時鐘差在數秒時延條件下的精度．

本文首先對MADOCA-LEX產品及特性進行簡要介紹,然后介紹了衛星鐘差穩定性分析和預報的方法,最后基于MADOCA-LEX提供的高頻GPS鐘差數據和阿倫方差對衛星鐘短期穩定性進行分析,并采用多項式模型和灰色模型進行短期鐘差預報,評價模型對不同類型GPS衛星鐘差預報的精度．

1 MADOCA-LEX產品

日本準天頂系統(QZSS)是由日本宇宙航空開發機構(JAXA)運營,自2017年2月28日起由日本內閣府(CAO)控制QZS-1覆蓋整個亞洲-大洋洲的區域性衛星導航系統．2018年11月1日,日本官方宣布QZSS開始正式提供LEX增強服務[10]．為滿足GNSS用戶實時精密單點定位(PPP)等高頻高動態應用的需求,JAXA基于MADOCA軟件平臺實時收集處理全球52個GNSS系統監測站的觀測數據,解算GNSS衛星的高頻軌道參數和衛星鐘差,并通過互聯網或QZSS衛星的導航頻段實時播發給地面接收機,為用戶提供不需要外部互聯網連接的實時PPP服務．

若用戶需要對產品質量進行分析,可以從JAXA的FTP服務器上下載包括 RTCM10403.2-SSR (ssrXXXXX.rtcm)、RINEX SP3(madocaXXXXX.sp3)格式的MADOCA產品(ftp://mgmds01.tksc.jaxa.jp/)．本文所用1 s采樣率的MADOCA實時鐘差改正產品格式為RTCM-SSR,電文類型為1058,實時GPS精密鐘差產品是通過廣播星歷計算的衛星鐘差和 MADOCA 實時鐘差改正產品恢復得到．

MADOCA-LEX產品的數據主要包括軌道、時鐘、差分碼偏差和用戶測距精度(URA)等信息,其中衛星軌道數據每30 s更新一次;鐘差數據每1 s更新一次,延遲一般為6～8 s;而URA則用于評估GPS、GLONASS、Galileo和QZSS的距離精度,每30 s更新一次;差分碼偏差的更新周期為1 d．該產品GPS衛星鐘差的目標精度為0.1 ns,實時定位誤差小于10 cm[5]．國內外學者已從該產品的鐘差精度[11]、可用性[10]和在PPP領域的應用[12]等多方面對MADOCA-LEX產品進行了分析,證實了該產品的定位服務精度能夠達到厘米級PPP應用的需求．

2 鐘差穩定性分析及預報模型

2.1 數據預處理方法

星載原子鐘在軌期間,因硬件故障或外界環境等因素,原始鐘差數據中不可避免地會出現粗差．為消除粗差數據對評估結果的影響,需對原始鐘差數據進行數據預處理[1]．數據預處理前,通常需要先將原始鐘差轉化為頻率數據．轉換公式為

(1)

式中:xi為i時刻鐘差數據;fi為頻率數據．考慮到較長時間的鐘差頻率數據的數據量較大,為提高效率,本文使用中位數法對粗差數據進行剔除,具體公式如下[13]:

MAD=Median{|yi-m|/0.6745},

(2)

式中,m=Median{yi},當觀測量|yi|>(m+n·MAD)時,將其標為粗差點,本文僅對數據進行n=3的粗差剔除的預處理操作．

2.2 基于阿倫方差的穩定性分析

GPS星載原子鐘主要有銣鐘和銫鐘兩種,其中銫鐘頻標輸出頻率頻漂接近于0,常使用阿倫方差[14]進行穩定度分析;而銣鐘長期頻漂較為明顯,一般采用哈達瑪方差[6]進行穩定度分析．但考慮到銣鐘短期內頻漂并不十分明顯[15],為保證各原子鐘穩定性分析方法的一致性,本文統一使用阿倫方差對衛星鐘穩定性進行分析,其公式表達如下:

(3)

2.3 參數估計模型

2.3.1 多項式模型(PM)

PM是短期鐘差擬合預報中應用最廣泛的模型之一,能夠較好地表征衛星鐘時頻特性,常應用于GNSS實時導航定位等應用的鐘差預報[1]．常用的多項式模型主要包括一階模型(LM)[16]、二階模型(QP)[17]和高階多項式模型．數學表達式如下:

xi=a0+a1(ti-t0)+a2(ti-t0)2+…+

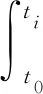
(4)

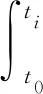
2.3.2 灰色模型(GM)

對于采樣間隔均勻的鐘差時間序列,可利用灰色模型進行建模和預報,其模型公式可表達如下[18]:

(5)

式中：x(0)(k)表示鐘差原始序列中的第k個數據,k=1,2,…,n;a、u為待確定參數,其值可以通過對樣本或樣本的衍生數列采用最小二乘準則求得．灰色模型的優點是只需要少量的已知數據就能建立模型;缺點是無法充分利用更多的已有數據來提高其預報精度．本文預報鐘差所用時間序列數據最少為5個,最多僅有30個,灰色模型具備可行性．

3 數據分析

3.1 算例數據

本文采用2020年1月1日-21日連續21天的1 s鐘差數據(MADOCA服務器1月24-28日處于維護狀態,數據產品中斷服務),對所有在軌GPS衛星鐘性能進行評估．由于MADOCA-LEX產品暫無最新的Block ⅢA衛星的鐘差產品,因而本文無法對最新的G04、G18衛星鐘差進行評估．為便于比較分析,將本文涉及的所有衛星分類列舉如表1所示.

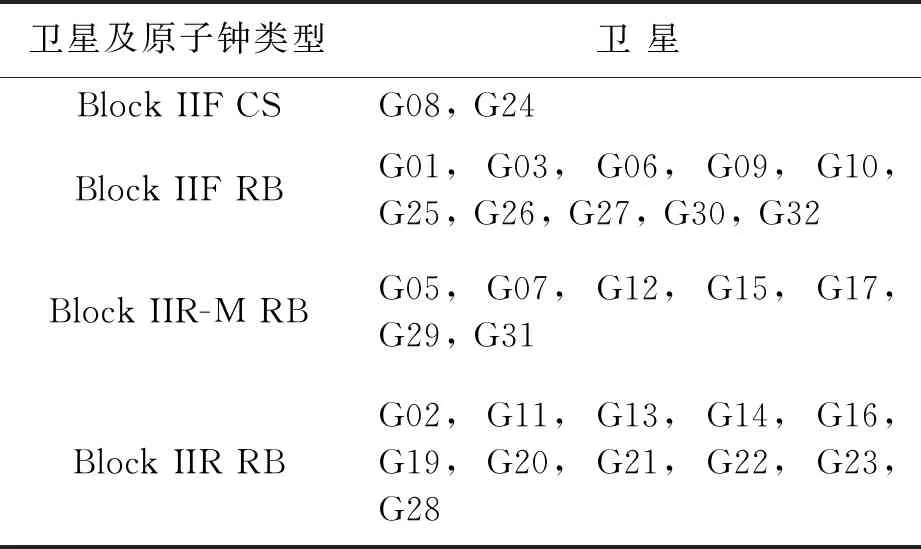
表1 本文涉及GPS衛星及原子鐘類型分類

3.2 穩定性分析

使用2020年1月1日-21日的數據,采用阿倫方差畫出原子鐘在[1,5,10,50,100,200,300,400,1000]s的穩定性結果如圖1所示．由圖可知,幾種不同類型衛星鐘差的10 s穩定性均在10-12s量級且5 s以內穩定性無明顯差異;就5 s以上的穩定性而言，配備銣鐘的Block IIF衛星鐘差穩定性的優勢逐漸體現,百秒穩在10-12到10-13量級,而配備銫鐘的Block IIF衛星鐘差穩定性略差于其他衛星．Block ⅡR-M鐘與Block ⅡR鐘差穩定特性整體上無明顯差異,千秒穩在10-13s,相較于Block IIF銣鐘而言,該鐘穩定性一致性要略微分散．圖1中體現的各種衛星100 s以上穩定特性與使用IGS中心提供的采樣率為30 s的數據分析的GPS衛星鐘穩定性的結論一致[19]．由于本文考慮的是實時PPP中,高頻鐘差在6～8 s的數據延遲情況下所存在的精度損失,因此主要關注原子鐘5～10 s時間間隔的穩定特性．

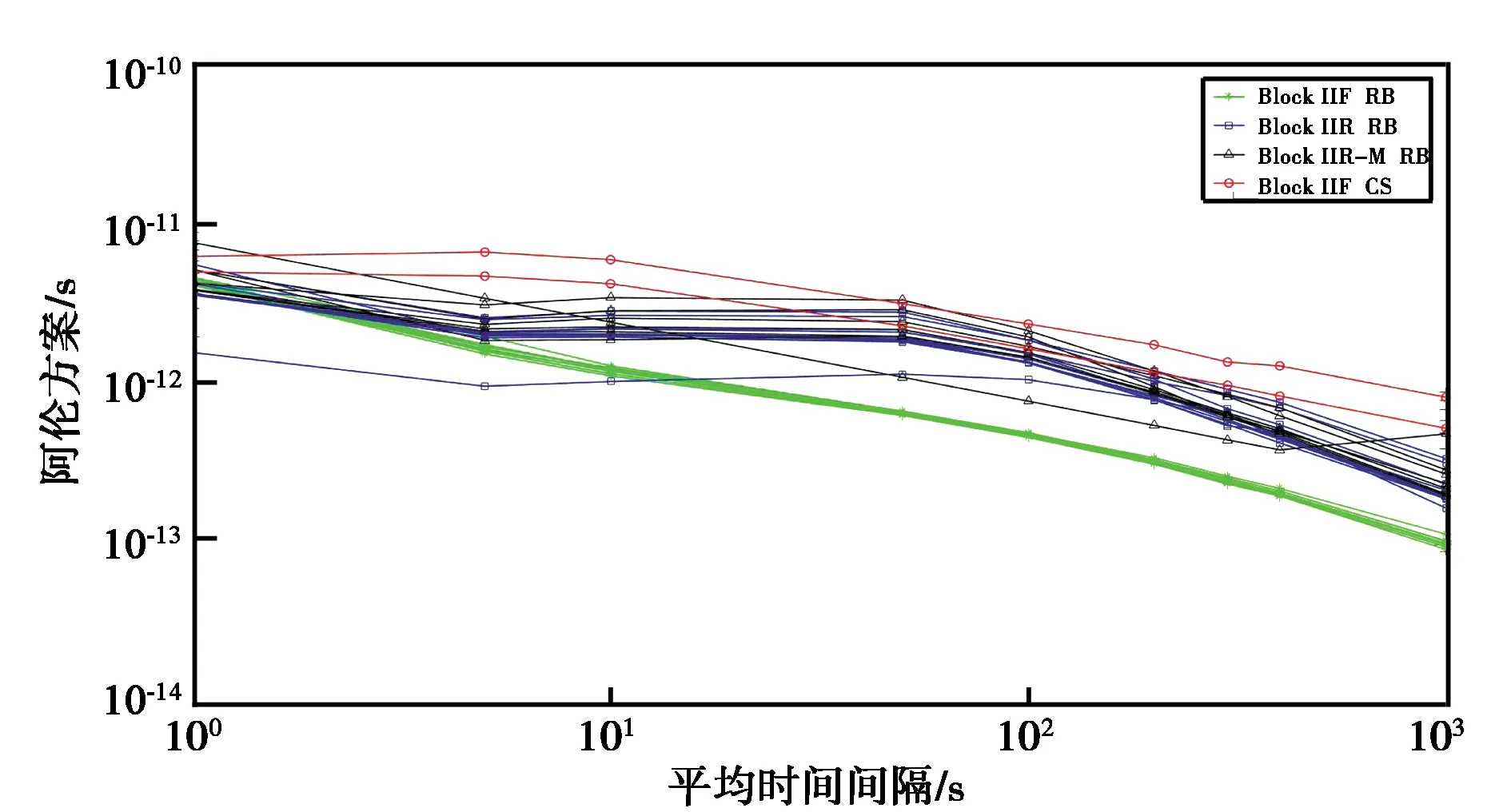
圖1 不同類型GPS衛星高頻鐘差穩定性

為驗證各種衛星鐘差多天的短期鐘差穩定性,本文以G08(Block ⅡF銫鐘)，G15(Block ⅡR-M 銣鐘),G21(Block ⅡR銣鐘),和 G32(Block ⅡF 銣鐘)4顆典型衛星為例,其2020年1月1日-21日連續21天的10 s穩定性對比如圖2所示:4種不同類型衛星鐘差的10 s穩定性都在10-12量級,且絕對數值無明顯變化,驗證了本文的鐘差產品穩定性分析的可靠性．

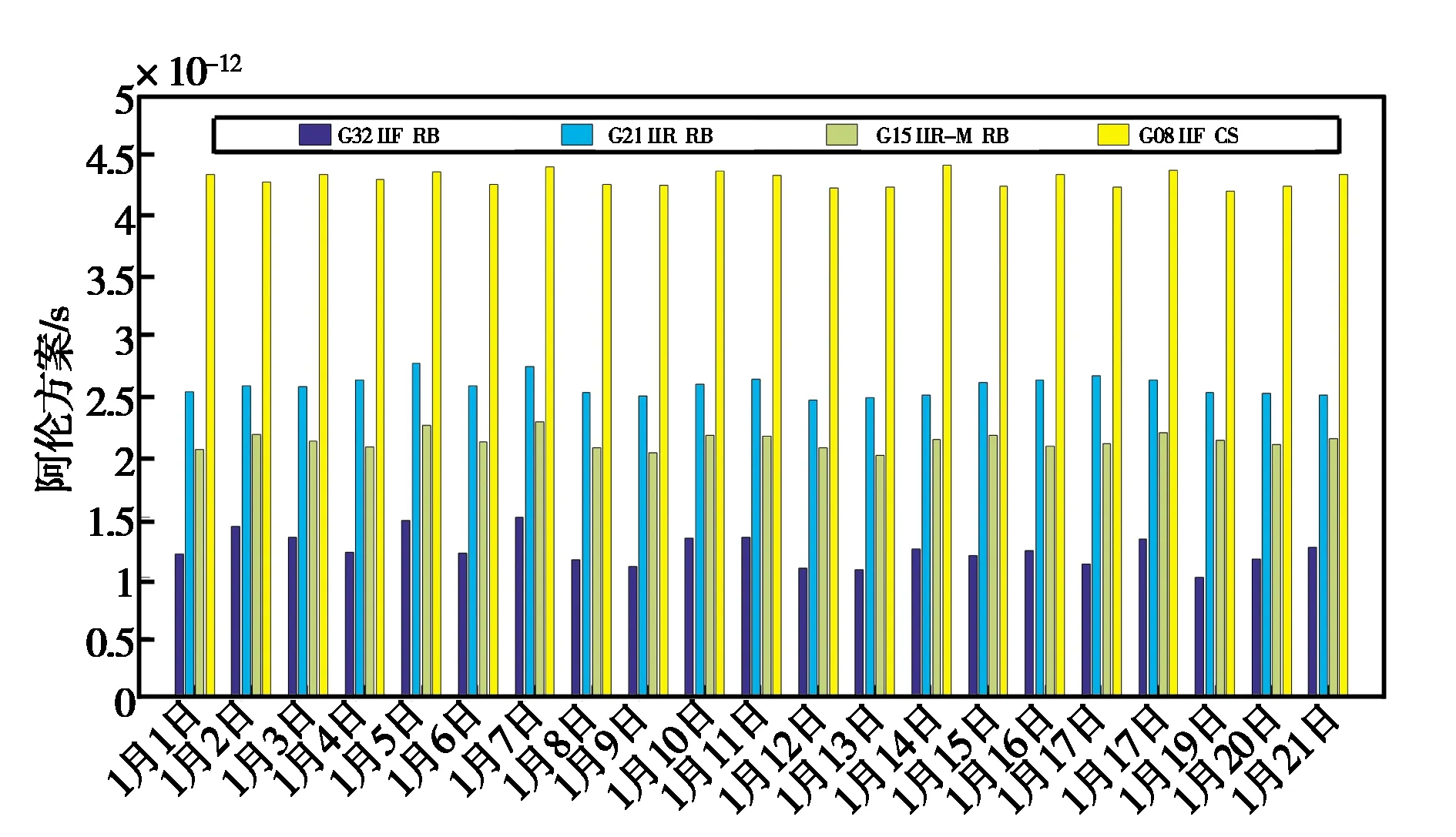
圖2 四顆典型GPS衛星單天鐘差的10 s穩定性

3.3 短期鐘差預報

分別使用LM、QP和GM對GPS衛星鐘差進行建模預報,評估不同擬合窗口長度對鐘差預報精度的影響．選取JAXA數據中心提供的2020年1月1日一整天的采樣間隔為1 s的實時精密鐘差數據,將全天86 400個歷元分別按照5 s,10 s和30 s間隔分為若干組,每組數據均采用LM、QP和GM建立鐘差預報模型并預測后續10 s時長的鐘差,然后以MADOCA-LEX提供的后續實際鐘差為參考值,評價預報鐘差的精度．本文選用預報殘差的均方誤差(RMS)作為衡量鐘差預報精度的指標,來比較不同模型和擬合窗口長度的精度差異．

首先使用5 s擬合窗口,分別采用LM、QP和GM模型建模,預報殘差的RMS值隨預報時長的變化趨勢如圖3所示:三種模型的預報精度都隨著預報時長增加而降低,且銫鐘精度隨時間衰減最為顯著,其中LM模型預報殘差的RMS值均在0.1 ns以內,GM模型的精度稍差,RMS值最大達到0.15 ns．QP模型預報精度較低,10 s后RMS值可達0.4 ns,此偏差折合測距誤差達到12 cm,無法保證厘米級的定位精度．

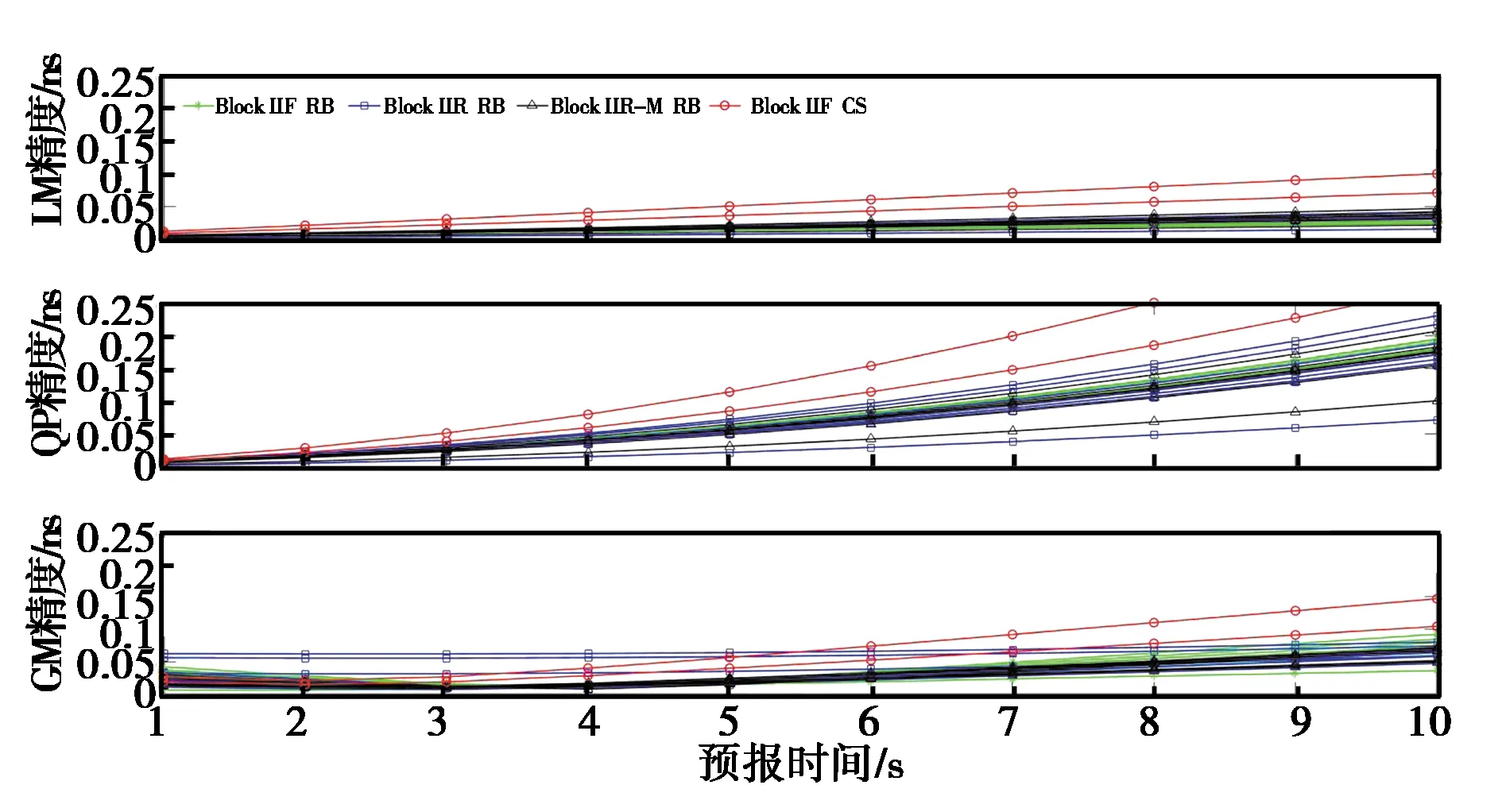
圖3 5 s擬合窗口長度10 s鐘差預報殘差RMS對比

將擬合窗口增加到10 s后,預報精度如圖4所示:三種模型的預測精度與使用5 s時長時基本一致,其中LM模型預報精度仍為最佳,RMS小于0.1 ns,QP模型的預報精度有較大提高,其RMS值大多低于0.2 ns,而GM預測模型則有兩顆RMS值接近0.2 ns的Block-IIR 銣鐘,預報精度較差,穩定性還有待提高．

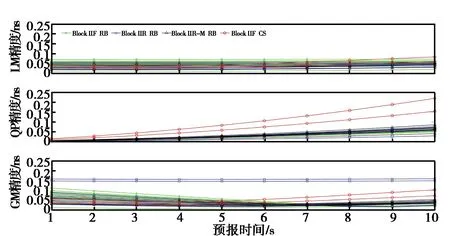
圖4 10 s擬合窗口長度10 s鐘差預報殘差RMS對比

擬合窗口再次增加至30 s時長的鐘差預報精度如圖5所示:QP模型的預報精度顯著提高,所有衛星的RMS值均低于0.1 ns．LM模型因未考慮鐘的頻漂特性,預報精度明顯退化,誤差可達0.4 ns;該現象在GM預報模型中體現得更為明顯,除兩顆精度明顯發散的Block IIR衛星以外,其他衛星預報鐘差的RMS值也接近0.5 ns．因此,使用30 s擬合時長進行鐘差預報時,QP模型精度要高于LM和GM模型．

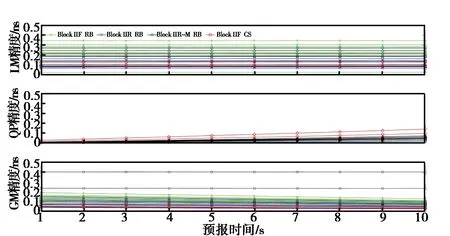
圖5 30 s擬合窗口長度10 s鐘差預報殘差RMS對比

上述基于不同種類衛星鐘差的短期預報對比結果可見,加載銣鐘的衛星鐘差預報精度整體略高于Block IIF銫鐘,與圖1鐘銣鐘10 s短期穩定性高于銫鐘一致．采用5 s和10 s擬合窗口時,一階線性模型即可得到較好鐘差預報精度,延遲10 s之后其預報精度仍然不超過0.1 ns．如采用30 s擬合窗口,則需要考慮衛星鐘的頻漂特性,因此采用QP預報精度更優,達到0.15 ns以內．灰色預報模型常見于鐘差產品的長期預報,本文的3種擬合窗口長度下短期鐘差預報中未體現優勢,不建議用于鐘差短期預報．

4 結束語

本文基于MADOCA-LEX產品提供的1 s采樣率的GPS精密鐘差,首先用阿倫方差分析各衛星原子鐘的短期穩定性,并用多天的數據比較不同類型GPS衛星鐘的多天10 s穩定性．然后分別使用LM、QP和GM對原子鐘10 s內的鐘差進行了預報和精度評估．分析結果顯示:

1)MADOCA-LEX提供的高頻鐘差產品5 s和10 s穩定性都達到了10-12量級,數據產品10 s以內漂移理論上不會超過0.1 ns;

2)采用5 s或10 s擬合時長窗口進行鐘差預報時,因衛星鐘差的頻漂都不明顯,LM模型相對于QP和GM模型而言預測精度最高且效果最為穩定;若采用30 s時長的窗口進行鐘差預報,QP模型因考慮了衛星鐘的頻漂效應,預測效果更為可靠．兩種模式的鐘差預測殘差RMS值都可達到0.15 ns以內,滿足厘米級PPP的需求．