基于NARX神經網絡的FPSO系泊纜張力預報

鄧林青， 朱耀文， 王宏偉， 張勇青， 李彤濱

(1. 中海石油深海開發有限公司，深圳 518067；2. 哈爾濱工程大學 船舶工程學院，哈爾濱 150001；3. 海洋石油工程股份有限公司，天津 300451)

0 引 言

浮式生產儲卸油平臺FPSO(floating production storage and offloading)在海洋石油勘探開發中被廣泛應用，一般采用系泊系統限制其在海面的運動。由于人類對資源需求的日益增長，海洋油氣的開發不斷走向深海，從而使浮式平臺及其附屬系統面臨更為惡劣的海況[1]。為了保證各類平臺的安全作業，浮式結構的運動響應范圍以及系泊纜的張力極值必須在規定的范圍之內。因此，在設計初期，需要借助復雜的時域耦合分析軟件，對復雜的外部環境荷載進行相應的計算與分析。在外部風、浪、流等載荷的聯合作用下，浮式結構運動與系泊及立管系統之間的耦合作用不能忽視，深水細長結構物顯著的動態特性也需要準確地模擬，這些因素將導致整個系統在時域仿真求解時需要耗費較多的計算時間。

當前已有大量的研究投入到尋求一個可靠的、耗時較少的浮式結構系泊系統耦合分析方法[2-4]。人工神經網絡是一種基于數據驅動的方法，在輸入與輸出之間起到了類似傳遞函數的作用，適用于尋找隨機輸入與相應輸出之間的映射關系，其在船舶與海洋工程領域已經得到了廣泛的應用，包括浮式結構及其系泊系統設計參數的優化，波浪有義波高、環境荷載、船舶運動的預報，纜線與結構的疲勞分析等[5-8]。Guarize等人[9]提出了一種基于人工神經網絡與有限元模型的混合方法，用于細長海洋結構物的時域動態分析，前期使用仿真軟件得出短時間內的結果，作為神經網絡的訓練數據，將已知的浮體運動輸入訓練好的神經網絡中進行張力預報，得到一個長期的時域響應。孫麗萍等人[10]將BP神經網絡和遺傳算法相結合，對FPSO系泊系統的長度進行優化，縮短了優化所需的時間。張隆輝等人[11-12]在構建系泊系統主動式截斷仿真過程中，使用NARX神經網絡模型代替了傳統纜索數值模型，用于預報系泊線截斷點的運動響應。該模型能夠加快計算求解的速度，有助于主動式混合模型試驗的實現。Pina[13-15]使用NARX神經網絡進行了系泊線和立管的力學分析。以浮體的運動為輸入參數，系泊和立管的頂端張力為輸出參數，通過對比神經網絡模型預報結果與有限元計算結果，驗證了該模型能夠準確地預報頂端張力，并具有較高的計算效率。隨后，將小波函數作為激活函數，使用小波神經網絡代替傳統的有限元仿真，進行海洋細長結構物的分析。上述方法均是基于預先規定的浮體運動，沒有考慮浮體與系泊系統之間的耦合作用。為此，本研究將波浪的時歷升高作為神經網絡模型的輸入參數，使用神經網絡模型進行浮式生產系統的時域耦合分析。

本文將NARX神經網絡應用于某一分布式FPSO系泊系統時域耦合分析中，該模型包括兩種訓練模式，序列并行模式(NARX-SP)與并行模式(NARX-P)。前者需要將當前時間步之前的真實輸出目標數據進行反饋，而后者需要將預報出的數據反饋回輸入層，由于輸出的真實目標數據無法提前得知，因此選取并行模式(NARX-P)進行訓練與預報。首先使用OrcaFlex軟件計算得到短時的時域耦合結果，以已知波浪的時歷升高數據作為輸入，系泊纜張力響應為目標輸出，使該神經網絡具有預報余下時間歷程張力響應的能力。經比較發現，預報結果與時域耦合分析計算結果之間的最大相對誤差為7.61%，而且該替代模型能夠大幅減小數值仿真的時間。

1 NARX神經網絡與實施方案

NARX神經網絡是一種動態的循環神經網絡，以誤差反向傳播的多層前饋神經網絡(BPNN)為基礎，引入了適當的延時參數與反饋作用。此神經網絡的輸出不僅取決于當前時間步的輸入，還受到過去幾個時間步神經網絡輸入、輸出值的影響，在一定程度上能夠緩解時域數據間存在的長期依賴問題，改善神經網絡的性能，適用于時域非線性動態系統的預報，其作為一種強大的時域預報模型已被廣泛地應用[16-17]。

1.1 神經元與激活函數

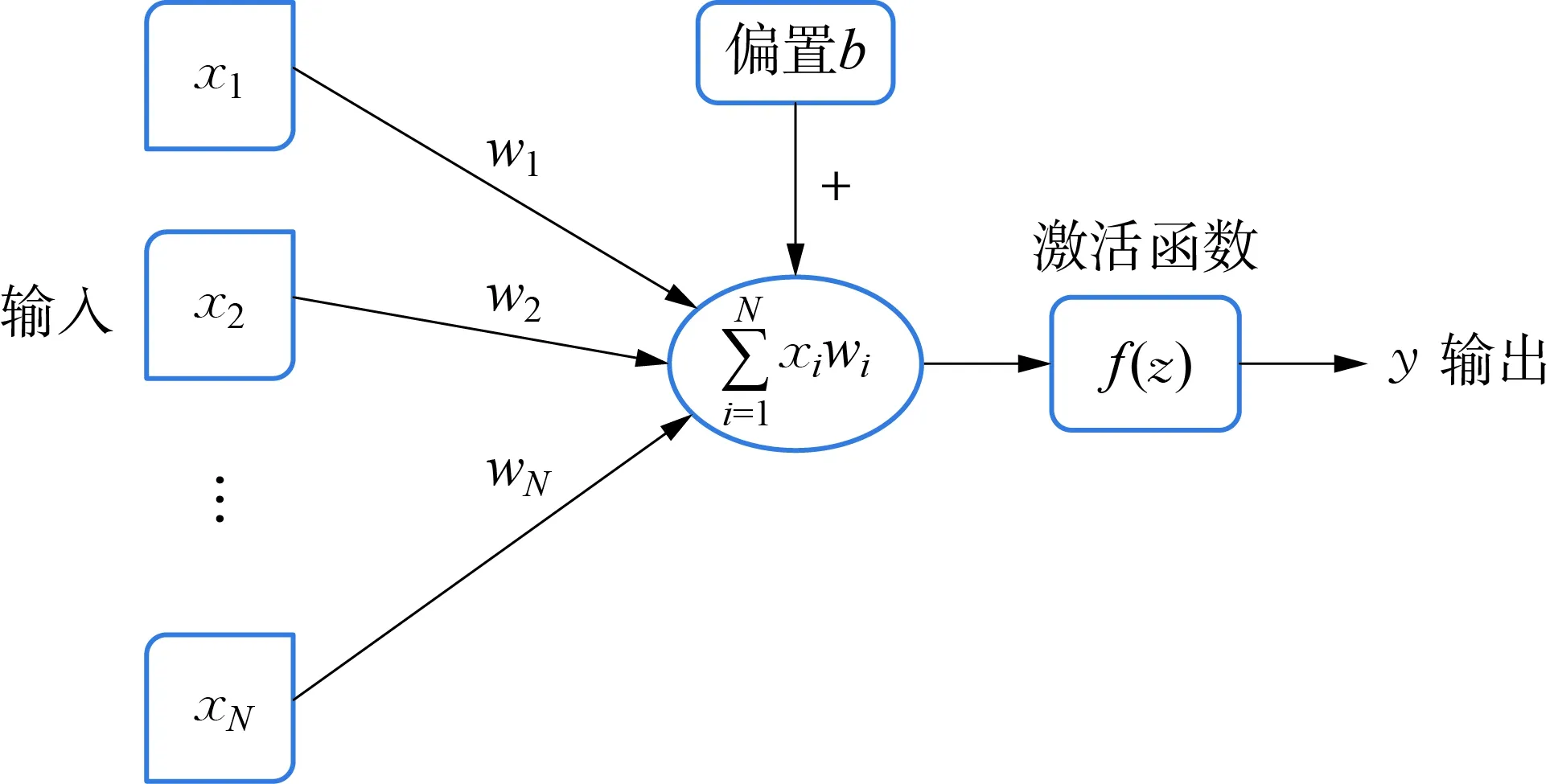
圖1 McCulloch-Pitts模型Fig.1 McCulloch-Pitts model

神經元是神經網絡的基礎，也是神經網絡的基本單元，其有興奮和抑制兩種狀態。在一般情況下，大多數的神經元處于抑制狀態，但是一旦某個神經元受到刺激，將導致它超過某個閾值，這個神經元就會被激活，處于“興奮”的狀態，進而向其他的神經元傳遞信息。1943年，心理學家McCulloch和數學家Pitts參考了生物神經元的結構，發表了抽象的神經元模型——MP模型，如圖1所示。MP模型接受已知特征數據的輸入xi，i=1，N，每個神經元使用權重wi、偏置b與輸入數據進行線性組合后得到權值輸出z，為了引入非線性特性，加權輸出還需經過激活函數f(z)的轉換得到輸出y。MP模型的建立為神經網絡的發展奠定了基礎，但是由于其預先定義的權值無法進行學習，后來逐步提出了單層感知器、多層感知器以及誤差的反向傳播算法。當前各種形式的神經網絡模型被不斷地提出，廣泛應用于各個領域。

神經網絡已有多種激活函數可供選擇，例如常用于分類問題的邏輯函數，以及用于回歸問題的線性整流函數。本文使用的是如圖2所示的雙曲正切激活函數，它是一個值域具有上下界的連續函數：

(1)

式中：y為輸出結果；z為加權輸出。

圖2 雙曲正切激活函數Fig.2 Hyperbolic tangent activation function

1.2 NARX神經網絡結構

基于圖3所示的雙層BP神經網絡(由于輸入層未進行任何變換，沒有作為單獨的一層考慮)只包含了一個隱藏層，圖4展示了NARX神經網絡的結構。當前的神經網絡輸出不僅取決于當前和過去的輸入，還取決于過去的輸出，其輸入集和最終輸出結果可以分別表示為

X(t)=(x(t),x(t-Δt), …,x(t-pΔt),
y(t-Δt), …,y(t-qΔt))

(2)

yt=f(w，X(t))

(3)

式中：x(t)為神經網絡的輸入；yt為輸出結果；w為權重參數；f(·)代表了NARX神經網絡結構建立的映射關系模型；Δt為時域耦合分析所用的時間步長；p和q分別為輸入與輸出反饋的延遲階數；pΔt和qΔt為延時的時間長度。輸入與輸出的延遲效應使得NARX具有了一定的記憶能力。

圖3 雙層BPNN結構Fig.3 Double-layer BPNN structure

圖4 NARX神經網絡結構Fig.4 NARX neural network structure

神經網絡模型輸入參數的選擇對于最終的結果有很大的影響。在浮式結構系泊系統時域耦合分析過程中，浮式結構水動力性能(AQWA軟件預先計算)與外部的環境荷載是已知的條件，但這些都是不變的常數項，為了能夠預報時域的輸出，需要有相應的時域輸入數據。文中選用波高的時歷曲線作為輸入，FPSO系泊系統的系泊線頂部張力值作為輸出。

需要注意的是，NARX神經網絡具有兩種訓練模式。第一種模式是序列并行模式(NARS-SP)，這種方式的輸入層由實際的目標值d(t)組成，即反饋回去的是實際的軟件仿真結果，可表示為

X(t)=(x(t),x(t-Δt), …,
x(t-pΔt),d(t-Δt), …,d(t-qΔt))

(4)

另一種模式為并行模式(NARX-P)，不同之處在于其將預報的輸出反饋到輸入層，如式(2)所示。在實際進行預報時，只有在訓練集與驗證集中的d(t)是已知的，可以通過OrcaFlex軟件進行短時的時域耦合分析得到，而測試集的結果則使用訓練完成的神經網絡模型進行預報。

本文使用神經網絡模型預報系泊線的頂端張力響應，以提高計算效率，減小時域耦合計算時間。由于無法得知當前時刻實際的張力值，因此使用NARX-P模式進行訓練和預報。后續提到的NARX神經網絡均表示使用NARP-P模式進行訓練與預報的模型，該模型使用MATLAB提供的神經網絡工具箱來完成[18]。

1.3 應用方案

如NARX此類的監督神經網絡均需要一定數量的訓練集進行訓練，再通過驗證集對模型的參數等進行適當的調整，最終運用到測試集上去預報未知的數據結果，這需要一個短時的時域耦合計算結果。同時，神經網絡模型對訓練集與驗證集上的輸入與輸出數據必須是已知的，由于FPSO及其系泊系統在時域耦合分析過程中無法預先得知船舶運動時歷數據，即無法使用船舶運動作為神經網絡的輸入參數。本文選擇波高時歷數據作為輸入，系泊線頂端張力作為輸出。

浮式結構系泊系統時域耦合運動模擬時間設置為3 h(10 800 s)，計算步長為0.1 s。首先使用OrcaFlex軟件計算800 s內的浮體系泊系統時域結果，其中600 s用于訓練，200 s用于驗證，每一個訓練周期后，該模型都會預報驗證集上的系泊張力，并與實際3 h數值模擬計算結果進行對比。如果在6個周期中驗證集上的誤差均呈現增長，則表明該模型無法繼續優化，即完成訓練，余下時間的張力響應可由建立的NARX神經網絡模型預報得出。為了驗證最終在測試集上的預報結果，文中進行了3 h的時域計算，實際使用時只需要計算短時目標數據(800 s)即可。實施方案如圖5所示，其中的誤差指的是均方誤差：

(5)

式中：n為輸入數據的數量；y(t)和d(t)分別為預報值和實際目標值。

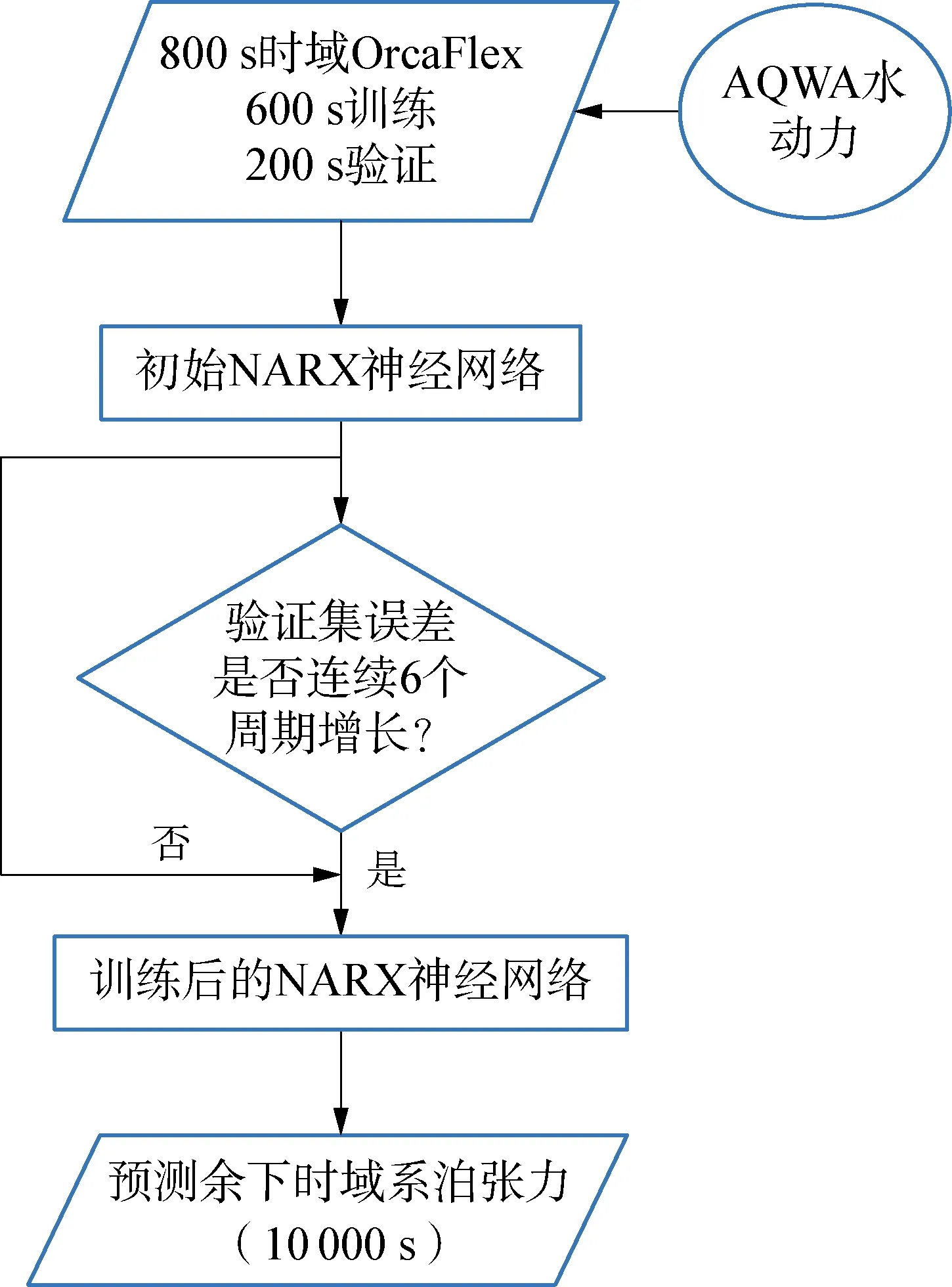
圖5 NARX神經網絡應用方案Fig.5 The application scheme of NARX neural network

2 數值計算分析

2.1 FPSO系泊系統模型與環境參數

上述方法被應用于某一分布式FPSO系泊系統，作業水深為1 200 m，平臺與系泊纜的具體參數如表1和表2所示，共有12根系泊纜，分為4組，每組3根。每根系泊纜均鏈條-鋼纜-鏈條三段材料構成，系泊編號及模型如圖6所示。系統受到210°方向的風、浪、流的聯合作用，表面流速為1.53 m/s，平均風速為25.6 m/s，波浪有義波高與峰值周期分別為7.25 m和19.78 s。在整個仿真過程中，流速與風速的大小和方向都是定常的，而波高是隨時間變化的。為了預報系泊纜張力的時歷輸出，使用波高時歷數據作為輸入。波浪采用JONSWAP譜，可定義為

(6)

式中:α為能量尺度參數；γ為譜峰升高因子；σ為峰形參數；ωm為譜峰頻率。

表1 FPSO平臺參數

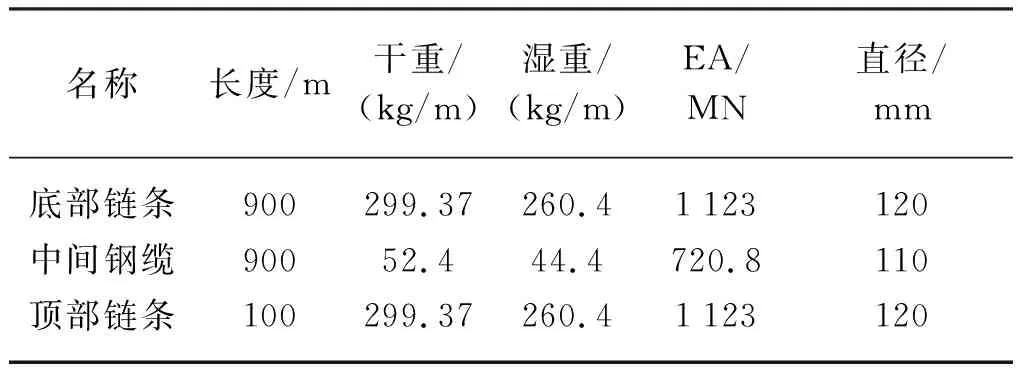
表2 系泊線參數

波浪譜確定后，即可以得到相對于空間某點的波面升高時歷曲線。在OrcaFlex軟件中可以得到整個時域過程的波高時域數據，這些數據在計算之前即可得知，這是前提條件。在實際應用時會發現，輸入多點的波面升高更有利于NARX神經網絡發現數據間的映射關系。因此，基于FPSO系泊系統靜態平衡位置(-48.5, -55.6)處的波面升高時歷曲線，再選擇(-28.5, -35.6)、 (-38.5, -45.6)、 (-58.5, -65.6)、 (-68.5, -75.6)，共五個點的波浪升高作為輸入參數。圖7給出了(-48.5, -55.6)位置處的波面升高時歷曲線，上述靜態平衡位置的計算也可以避免時域耦合分析時浮式平臺的瞬態效應，防止不合理數據的生成。

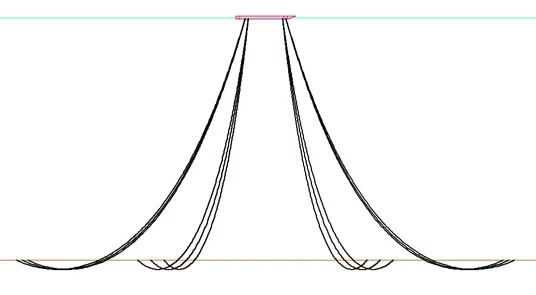
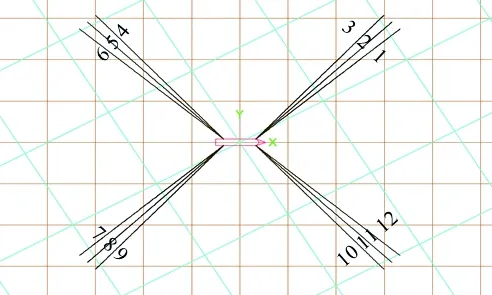
圖6 FPSO系泊系統模型

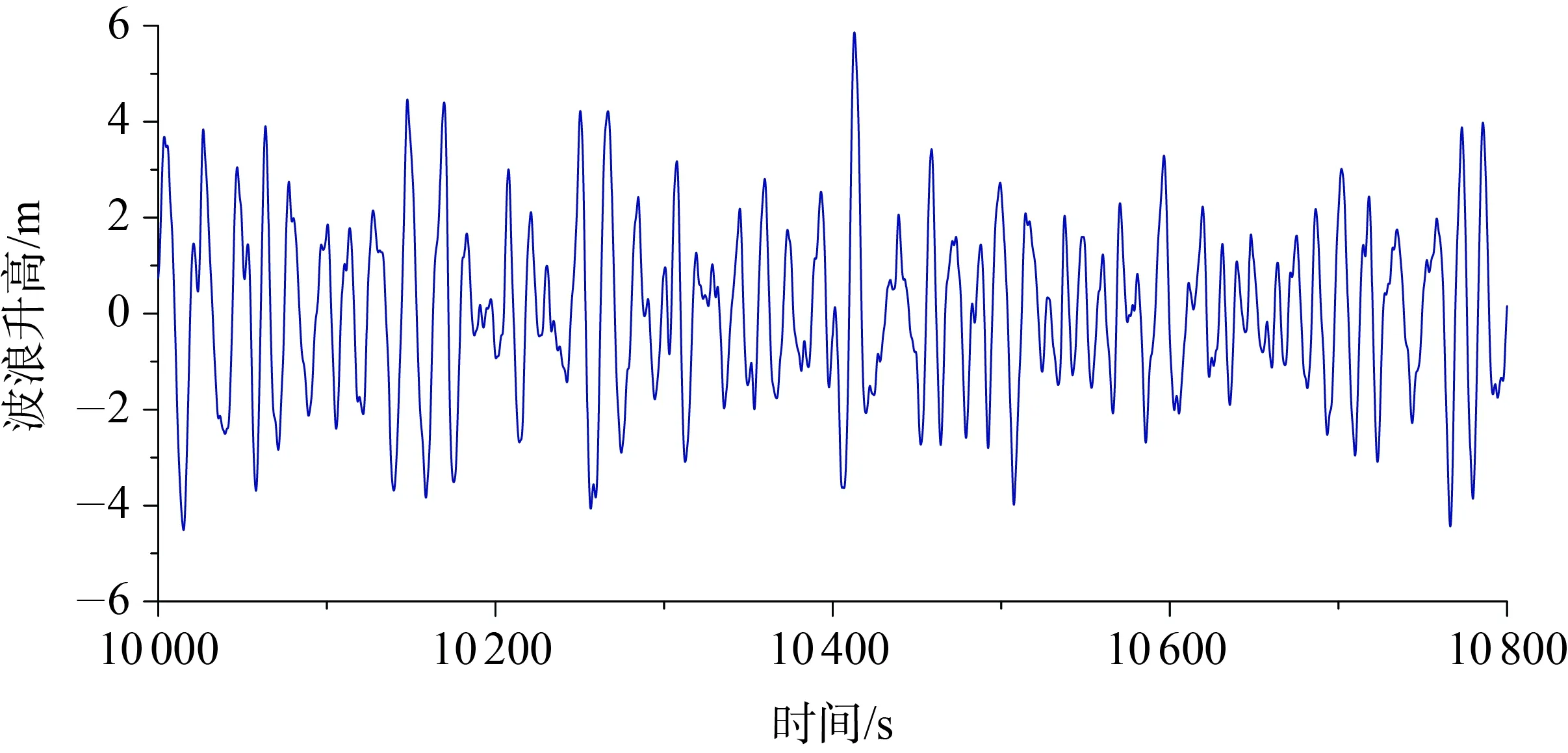
圖7 波浪升高時歷曲線Fig.7 Time history of wave elevations

2.2 超參數設定

首先使用OrcaFlex計算800s內的時域耦合數據，作為NARX神經網絡的訓練集和驗證集。隨后，需要確定該模型的輸入與輸出延遲數，以及隱藏層的神經元數量，這些超參數對神經網絡模型的性能有很大影響。采用試湊法對隱藏層數和延遲數分別為5～20和5～30，間隔為5的區間范圍內進行搜索，尋找結果較優的超參數，輸入與輸出使用相同的延遲數。選用系泊纜Line3，由于系泊纜張力量級較大，為了清晰地表示真實值與預報值之間的誤差，表3展示的為均方根的誤差。此處只給出了部分結果，當隱藏層神經元數為20時，輸入與輸出的延遲數為15時，均方根誤差最小，為87.92 kN。在此過程中，NARX神經網絡的訓練也已經完成，當相應超參數確定后，即可用此參數下的NARX模型對測試集上的系泊纜張力進行預報。

一般神經網絡的學習能力能夠隨隱藏層數與延遲數的增大而加強，但是太過復雜的神經網絡結構會導致在訓練過程中的過擬合問題，使其在驗證集上的性能反而不好。網絡層數太少又會導致訓練時的欠擬合，使得該神經網絡無法學習到輸入和輸出之間的關系。因此，對于超參數的正確選擇是神經網絡模型能否有效的關鍵因素之一，此處采用試湊法確定了一個較優的神經網絡模型結構。

2.3 結果與分析

使用訓練好的神經網絡模型去預報余下10 000 s系泊纜Line3的時域張力結果，在此基礎上，可以使用相同的神經網絡結構進行系泊纜Line4的訓練和預報。分別使用OrcaFlex軟件和神經網絡模型進行計算，圖8～圖11分別展示了2 000～2 400 s和10 400～10 800 s的Line3和Line4張力時歷曲線對比結果。可見，預報結果與目標值(OrcaFlex軟件計算結果)之間的時歷曲線趨勢幾乎完全一致，結果吻合良好，但在每個時間段的峰值上略有差異。兩種計算方式在時域結果上的相對誤差如表4和表5所示，其中系泊纜頂端張力平均值的相對誤差較小，系泊纜Line3和Line4張力最小值的相對誤差分別為7.10%和7.61%，張力最大值的相對誤差分別為5.33%和5.81%。整體上，相對誤差的最大值為7.61%，在可接受的范圍內。

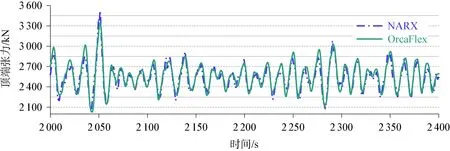
圖8 Line3頂部張力時域曲線2 000～2 400 sFig.8 Line3 top tension time series 2 000～2 400 s

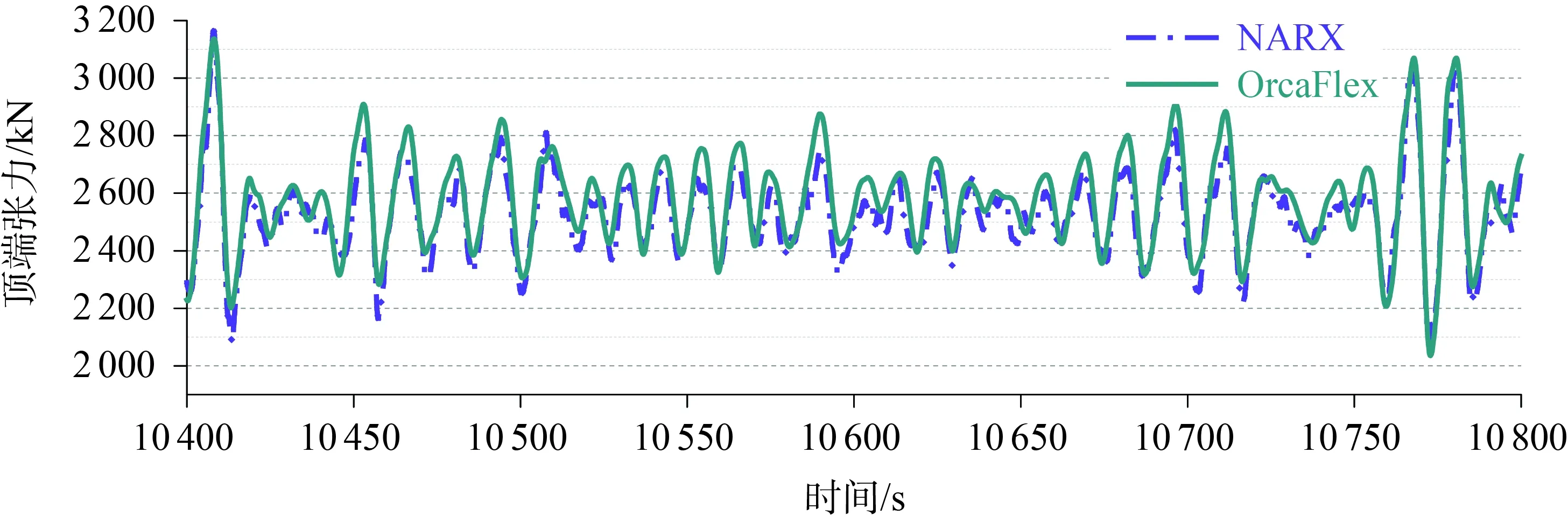
圖9 Line3頂部張力時域曲線10 400～10 800 sFig.9 Line3 top tension time series 10 400～10 800 s

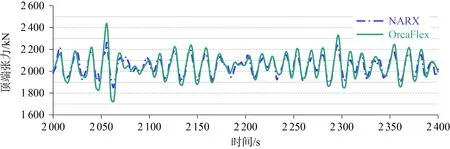
圖10 Line4頂部張力時域曲線2 000～2 400 sFig.10 Line4 top tension time series 2 000～2 400 s

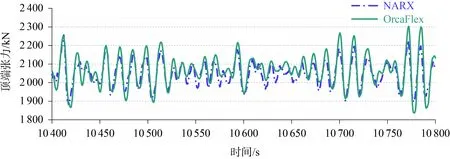
圖11 Line4頂部張力時域曲線10 400～10 800 sFig.11 Line4 top tension time series 10 400～10 800 s

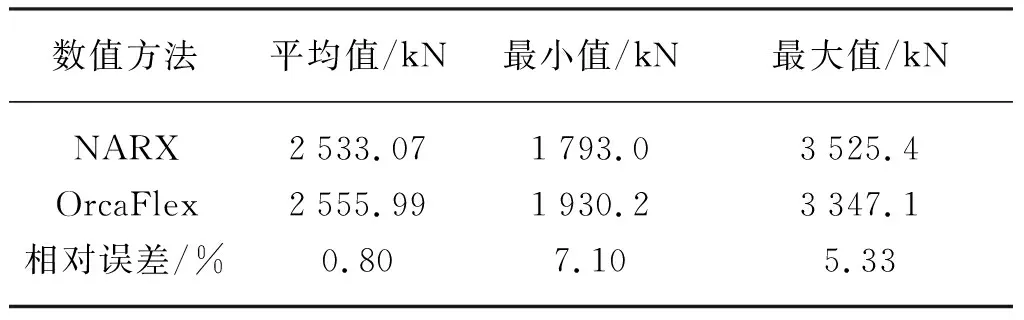
表4 Line3頂部張力時域數據分析

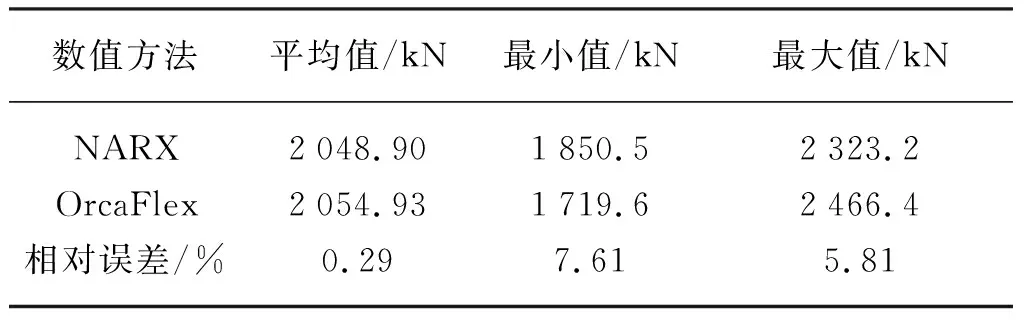
表5 Line4頂部張力時域數據分析

此種方法只需計算短時(800 s)時域耦合分析數據，使用神經網絡模型預報其后10 000 s的系泊纜頂部張力，可以大幅減小OrcaFlex軟件進行浮式結構系泊系統時域耦合分析的時間，計算效率大約為常規方法的13倍。這里的計算效率沒有考慮神經網絡構建以及訓練、預報的時間，其中神經網絡的構建，包括文中提到的超參數的選擇會耗費相對較多的時間。但是，對于同一類的問題，使用相同或相近的網絡結構，也可以得到較好的結果。本文中的神經網絡結構與相關文獻所用結構十分接近[13]，使用了具有20個神經元的單隱藏層、延遲數為15的神經網絡結構。

3 結 語

以某一分布式FPSO系泊系統為例，基于NARX神經網絡模型進行FPSO系泊系統耦合分析中系泊纜頂部張力預報，對比OrcaFlex軟件計算結果與NARX神經網絡模型預報結果，可知兩者的最大相對誤差為7.61%。此方法是將OrcaFlex軟件仿真計算與NARX神經網絡模型相結合的一種方法，可以大幅減小軟件時域耦合分析的時間，計算效率大約為常規方法的13倍。但是，文中使用的NARX神經網絡模型只適用于上述浮式平臺系泊系統的張力預報，如果需要更換浮式平臺以及系泊系統的參數，則需要重新對該神經網絡模型進行訓練。