基于MAA全溫滯后模型的MEMS陀螺儀零偏補償技術

吳 英，蔣 博，邸 克，鄒新海，劉 宇

1. 重慶科技學院 智能技術與工程學院, 重慶 401331; 2. 重慶郵電大學 智能傳感技術與微系統重慶市高校工程研究中心，重慶 400065)

0 引言

隨著微機電系統(MEMS)技術的持續發展，MEMS陀螺儀技術逐漸成為人們的研究熱點[1]。MEMS陀螺儀具有體積小、精度高、壽命長等優點，被廣泛用于慣性導航與定位領域[2]；但也存在初始安裝校準時間較長，器件材料對溫度較敏感，角度積分誤差隨時間累積等缺點[3-4]。由于MEMS陀螺儀內部構造材料膨脹系數的差異會產生相應的熱阻值和熱應力[5-7]，環境溫度的變化對陀螺零偏穩定性影響較大。

研究者從多方面對零偏補償進行了研究，典型的補償方法有：恒定參量激勵法、滑動平均法及多元向量回歸法等。文獻[8]采用一種基于恒定參量激勵的驅動控制方案，改善了小范圍溫度下降時陀螺儀溫度敏感性，但缺少在寬溫范圍內的溫度實驗結果。文獻[9]利用滑動平均法(MAA)對陀螺信號進行趨勢項提取，減小了輸出信號的時延問題。文獻[10]使用一種基于支持向量回歸的多元溫度補償方法，建立基于溫度梯度的多元補償模型，但在溫度轉折點處補償效果較差。

以上研究僅對溫度建立一個單一擬合曲線，對復雜溫度變化下MEMS陀螺的零偏補償效果較差。當環境溫度升降循環變化時，陀螺的零偏誤差并不是一條重合的曲線，而是多條有一定滯后偏移距離的曲線。

基于此，針對傳統的MEMS陀螺儀的溫度補償模型難以解決由溫度滯后變化引起零偏誤差的問題，本文提出了一種基于MAA全溫滯后模型的MEMS陀螺儀零偏補償技術。

1 陀螺儀全溫滯后模型

1.1 溫度滯后原理

溫度誤差是 MEMS 慣性器件的主要誤差之一。當環境溫度變化時，材料熱擴散速度有差異，引起陀螺結構尺寸、材料彈性模量和振動頻率變化，從而引起零偏變化。溫度的滯后性主要源于慣性器件的不同組成材料的熱阻值和熱應力各不相同，如緩沖膠的單位熱阻值比陶瓷管的單位熱阻值約高3個數量級。另外，由于溫度傳感器在固體上的空間位置不同而引起的測量誤差，慣性裝置中的金屬和陶瓷外殼的溫度滯后于傳感器裝置的輸出溫度，這也導致了溫度滯后現象。

1.2 全溫滯后模型

圖1 全溫滯后模型示意圖

在安全額定溫度范圍內陀螺儀進行溫度實驗，溫度滯后零偏的變化近似于梭型(或橄欖球型)。全溫滯后模型示意圖如圖1所示。由圖可見，其形狀飽滿、近似橢圓，反映出該結構的塑性變形能力和吸收震動能量的能力較強，具有良好的延展性。

首先設定30 ℃時的靜態零位角度值作為溫度誤差基準值；然后溫度循環實驗測得的零偏值減去溫度誤差基準值，即為由溫度變化引起的溫度零偏值。在升降溫度循環實驗中，當溫度回到30 ℃時，零偏B1、B2并未回到0 (°)/s，這種情況是由于溫度的滯后性導致的現象，它將嚴重影響系統輸出航向精度，因此需要對升溫和降溫分別建立補償曲線，建立升降溫度滯后零偏補償模型，從而提高陀螺在環境溫度循環變化下的零偏穩定性，減小溫度滯后對陀螺儀精度的影響。

2 基于MAA全溫滯后模型的零偏補償技術

2.1 滑動平均算法

在離散動態實驗數據中，利用區間離散點的函數值表示研究對象的真實變化規律。為了消除動態實驗數據里的隨機噪聲波動，對于非平穩的陀螺儀數據，在一定長度的小區間上認為是穩定的。對其做局部求平均值的處理，過濾掉數據中的隨機噪聲，從而得到較平滑的數據曲線，即滑動平均算法。

在處理陀螺儀零偏數據過程中，對于一個長度為M的有序數據集合，按順序滑動選取r個相鄰數值，對每一個數值乘以一個比例權重系數，并相加求和，得到平滑的數據。

(k=p+1,p+2,…,M-q)

(1)

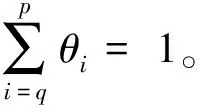
(k=s+1,s+2,…,M-s)

(2)

當p=0，q=r-1，θi=1/r，即左端點等權平滑法：

(3)

當p=-r+1，q=0，θi=1/r，即右端點等權平滑法：

(4)

本文對陀螺零偏數據采用右端點等權平滑法，如選取滑動步長r=9，通常用前9個零偏數據的均值來等效替換表示右端點，即第9個數據的測量結果：

g7+g8+g9)

(5)

對于滑動步長為r的右端點等權平滑法，它可以得到右端全部的值，但缺少左端頭部的平滑濾波值，稱為端部效應，即在區間[1,r-1]里的r-1個測量數據無法按公式(4)直接得到，需要額外補充錄入。

2.2 全溫滯后模型的零偏補償技術

分析陀螺儀靜態時溫度零偏的滯后性，采用滑動平均算法對陀螺儀信號進行數據提取，提出一種升降溫度滯后零偏補償模型。對不同溫度下的MEMS陀螺儀零偏進行標定，達到在全溫變化范圍內對陀螺儀零偏的精準補償目標。MEMS陀螺儀的MAA溫度滯后零偏補償模型Hω(T)為

(6)

式中：f0，f1，f2，f3為擬合系數函數；T為MEMS陀螺儀溫度；dT/dt為MEMS陀螺儀溫度變化率。

實驗中采樣得到的數據都是離散化的，計算dT時，利用ΔT(現在時刻溫度值減去前一時刻溫度值)近似表示，即dT/dt=ΔT/Δt，其中設定采樣頻率為1 Hz，Δt為定值。因此，MAA溫度滯后零偏補償模型可近似簡化為

(7)

由于升溫和降溫時的零偏值有差異，若用傳統單一曲線來擬合升降溫度的零偏，得到的零偏誤差較大。因此，不僅要采集此刻的溫度值，還要考慮前一時刻的溫度值，MAA升降溫度補償模型流程圖如圖2所示。本文以當前陀螺儀溫度值T和溫度變化率ΔT(此刻溫度值減去前一時刻溫度值)作為判斷條件，分別通過傳統補償模型、升溫模型(ΔT>0)和降溫模型(ΔT<0)來補償零偏誤差。

圖2 MAA升降溫度補償模型流程圖

3 實驗與分析

3.1 實驗過程

本實驗選用SCR系列陀螺，ESPEC系列SET-A-04型號溫箱，數據采集頻率為1 Hz ，整體實驗流程圖如圖3所示。

圖3 整體實驗流程圖

實驗步驟主要分為4步：

1) 溫箱恒溫30 ℃，對陀螺預熱30 min。

2) 以1 ℃/min的速度持續升溫，溫度上升至90 ℃，保持恒溫運行30 min。

3) 以-1 ℃/min的速度持續降溫，溫度降至-30 ℃，保持恒溫運行30 min。

4) 重復2)、3)步實驗30次。

在安全額定溫度-30～+90 ℃進行實驗，其中實驗循環1次的時間-溫度曲線圖如圖4所示。

圖4 實驗循環1次的時間-溫度曲線

3.2 零偏補償實驗結果分析

首先選取局部溫度變化區間-30～0 ℃和時間段 210～300 min的零偏變化數據進行分析，對應的局部時間、溫度、零偏擬合曲線如圖5所示。由圖可見，溫度從0降溫至-30 ℃，保持-30 ℃恒溫30 min，再升溫至0。無滯后曲線的零偏隨溫度呈單一線性變化；有滯后曲線的零偏隨溫度呈現復雜曲線變化，在溫度上升和下降趨勢發生變化時，會暫時保持原有狀態，從而出現溫度滯后零偏的情況。滯后區間對應的時間持續約5 min，溫度零偏相差約0.02 (°)/s。

圖5 局部時間、溫度、零偏擬合曲線圖

選取全溫變化區間-30～+90 ℃的零偏數據進行整體分析，先對傳統補償模型進行試驗，根據陀螺儀升溫與降溫時的初始零偏數據計算出平均擬合曲線，接著代入傳統補償模型得到補償后的升降溫度零偏輸出值，對應的傳統零偏補償前、后對比圖如圖6所示。傳統補償前的初始升溫、降溫曲線是在-0.5～+0.5 (°)/s波動的傾斜曲線，而通過傳統校準擬合曲線補償后，變成在-0.1～+0.1 (°)/s波動的近似水平曲線。

圖6 傳統零偏補償前后對比圖

對MAA補償模型進行試驗，根據陀螺初始零偏數據計算出校準擬合升、降溫曲線，代入MAA升降溫度滯后零偏補償模型得到補償后的零偏值，對應的MAA零偏補償前、后的對比曲線如圖7所示。通過MAA校準擬合曲線補償后，變成在-0.04～+0.04 (°)/s波動的近似水平曲線。

圖7 MAA零偏補償前后對比圖

分析對比MAA補償法與傳統補償法的結果，對應的陀螺儀零偏補償前、后參數變化情況如表1所示。零偏補償前的零偏標準偏差為0.21 (°)/s。通過傳統零偏補償后的零偏標準偏差為0.06 (°)/s，其減小了近3倍；通過MAA零偏補償后的零偏標準偏差為0.02 (°)/s，其減小了近10倍。由表可見，在減小溫度滯后零偏誤差方面，MAA補償法優于傳統補償法，提高了近3倍。

表1 零偏補償前、后參數變化表

4 結束語

本文針對傳統的MEMS陀螺儀的溫度補償模型難以適應溫度滯后變化的問題，我們利用滑動平均算法建立溫度滯后模型，采集升、降溫情況下的零偏數據，并做出擬合曲線，對陀螺儀的零偏進行校準補償。在-30～+90 ℃全溫范圍內的實驗表明，通過MAA升、降溫滯后零偏補償模型，可將陀螺儀零偏標準偏差從0.21 (°)/s 降至0.02 (°)/s，零偏穩定性增加了近10倍。通過MAA全溫滯后模型的零偏補償技術，可以適應全溫范圍的溫度變化，有效提高了MEMS陀螺儀的零偏穩定性和測量角度精度。