三段式撲翼飛行器氣動特性的仿真研究

趙衛凱,李文彬,黃 燦,吳 杰

(南京理工大學智能彈藥技術國家重點實驗室， 南京 210094)

撲翼飛行器在低雷諾數下的氣動特性是其研究過程中的一大難點，早在1909年Knoller和Betz[1]發現二維翼型在撲動過程中可同時產生升力和推力；1975年Weis-Fogh解釋了昆蟲升力產生的拍合機制[2]；1997 年,Van Den Berg 等在對飛蛾飛行的研究中發現了“延時失速” 機制[3],并在后來被Dickinso等在果蠅模擬實驗中得以證實；曾理江等研究蜜蜂飛行時翅膀的氣動特性[4]；孫茂等用Navier-Stokes(N-S)方程計算了柔性翼的氣動特性[5]；黃鳴陽、昂海松等設計出了一款多段柔性仿鳥折疊翼模型[6-8]。

目前，對撲翼飛行器的氣動研究主要依靠數值模擬和風洞實驗，且研究對象多為仿昆蟲的單段式撲翼，建立的撲翼模型為“拍動+扭轉”的兩自由度模型。近年來，通過分析鳥類翅膀的拍動過程，在撲翼模型中引入折疊這一運動，建立了“拍動+折疊+扭轉”的三自由度模型[9-10]。

以往的單段翼模型[11]是以小翼展、高頻率拍動的昆蟲為仿生對象，主要描述的是撲翼沿翼展拍動運動和沿翼弦的扭轉運動，并不適用于鳥類這樣的大型飛行生物，因為該模型也未考慮過鳥類翅膀拍動過程中的彎曲折疊問題。近年來建立的兩段翼模型[12]具有3種運動：翼展方向的拍動，翼弦方向的扭轉和內外翼之間的彎曲折疊，并采用分段建模的方式來達到近似柔性的效果。

本文以鴿子為研究對象，建立“拍動+內折疊+外折疊+扭轉”的三段式撲翼模型，用XFlow仿真軟件進行氣動仿真，主要研究低雷諾數下，三段式撲翼的各參數對飛行器氣動力的影響，為三段式撲翼的設計奠定基礎。

1 三段式撲翼模型的建立

1.1 鴿子飛行的高速攝影的分析

對鴿子的飛行過程進行高速攝影，觀察各個飛行周期內鴿子翅膀的拍動圖片。分析發現以往的兩段式撲翼模型只解決了鳥類翅膀拍動過程中的內外翼的主動折疊問題(內折疊角，圖1中的A處)，但并未考慮到鳥類在實際飛行中，在氣流的作用下，翅膀周圍的羽毛會因自身的柔性而發生被動折疊(外折疊角，圖1中的B處)，本文主要研究的是翼尖羽毛的被動展向折疊現象，分析內外折疊角共同作用下撲翼的氣動特性。

圖1 鴿子高速攝影圖片

因此，本文建立一個簡化的三段式撲翼模型，來描述翅膀撲動過程中的這內外折疊現象。

1.2 三維建模

針對上述分析的主要現象，進行適當的簡化，建立的三維模型主要包括機身和左右兩翼，撲翼由翼根到翼尖依次分為A、B、C三段，其中內翼為A段，翼展為100 mm，外翼由B、C兩段組成，合翼展為200 mm，翼根處翼弦為100 mm，A、B兩段連接處翼弦為200 mm，且A翼面為梯形，B、C兩段共同組成四分之一橢圓，如圖2所示。

根據對鴿子飛行過程高速攝影得到的圖像進行分析，可將撲翼飛行的復雜運動簡化為：翅膀上下拍動和扭轉、內外翼的折疊、翼尖折疊，三維模型如圖3所示。

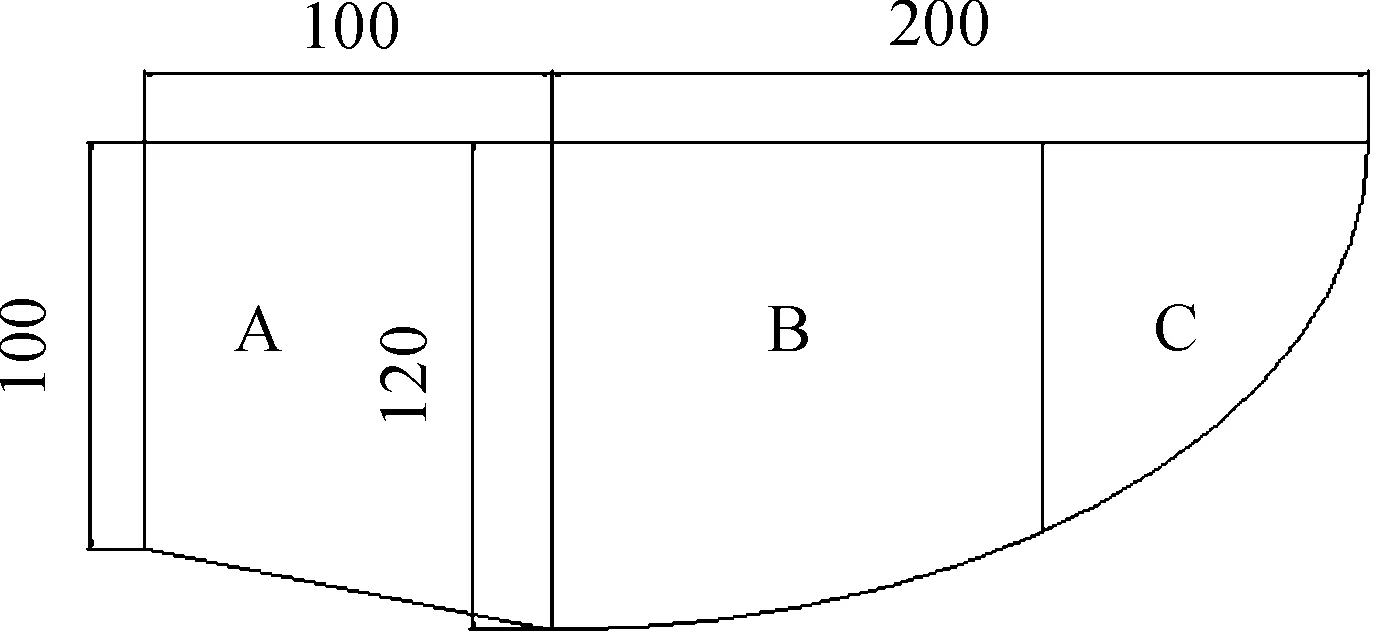
圖2 右翼面二維平面圖

圖3 撲翼飛行器的三維模型示意圖

圖3中β是內翼的拍動角，δin和，δex分別為撲翼的內外折疊角，還有撲翼的扭轉角設為α。其中扭轉角為翅膀繞翼展方向轉動時，內翼面與機身水平面的夾角。

撲翼截面應選用帶弧形彎曲的翼型[13]，此處采用上表面弧形、下表面內凹的S1223翼型，文獻[14]對6種翼型進行仿真對比，發現S1223具有最大的升力系數，適中的推力系數。飛行器的三維模型如圖3所示，其中機身長300 mm，翼展660 mm，內翼展為100 mm，外翼展為200 mm。

另外鳥類翅膀撲動會發生柔性變形，建立剛柔性混合撲翼模型，其中A段翼定義為剛性翼，B、C兩段按適當寬度分段建模，模擬撲翼的柔性部分。

2 撲翼運動模型的定義

2.1 拍動函數

本文以分段建模為基礎，A、B、C三段分別代表撲翼的內翼、外翼、翼尖，并分別列出各自的運動方程。其中A段翼只描述翅膀的拍動，B段翼描述拍動角和內折疊角，C段翼描述拍動角和內外折疊角。此外，撲翼飛行還需要考慮急回特性，即下撲階段所占時間為整個撲動周期的60%～80%，此處選為75%，對撲動過程的語言描述如下：

1) 下撲階段：翅膀由最高處開始下撲，在最高處，各段翼保持平直，隨后，在下撲過程中，內外折疊角逐漸展開，達到最大值后，保持內外折疊角度最大值繼續向下撲動，快到最低處時，折疊角緩慢收斂，在最低處，折疊角歸0，各段翼又保持平直。在下撲的同時，翅膀做扭轉運動，從而產生向前的推力。

2) 上撲階段：翅膀到達最低處后，撲翼向內折疊，快速上撲，內外折疊角也是緩慢打開，保持最大，然后收斂的過程，但因為急回特性的存在，這一過程相對于下撲階段的要快。同樣，在上撲的同時，翅膀也在做扭轉運動，產生推力。

綜上，結合急回特性和分段近似柔性的思想后，各翼段的撲動函數如下所示：

1)A段翼，參考文獻[11],以單段翼撲動函數為模型：

(1)

2)B段翼，與A段翼之間會有一個內折疊角：

(2)

(3)

(4)

其中，內折疊角為：

δin=δ1

(5)

βBx(t)表示B段翼中第x小段機翼撲動角函數，xB為B段翼的第x小段，nB表示B段翼共分為nB段，βB(t)表示B段翼末端處的撲動角函數。

該段翼參考了分段近似柔性思想，并從鴿子飛行的高速攝影圖像分析，發現無論在上拍，還是下拍階段，內折疊角都有一個完整的展開、保持最大、收縮的過程，因此，內折疊角作為一個獨立的函數存在，有自己的折疊幅值，且折疊頻率應大于內翼拍動頻率，不再用內翼撲動函數的相位差形式[12]來描述；

3)C段翼，與B段翼之間會有一個外折疊角：

(6)

(7)

(8)

其中，外折疊角為：

δex=δ2-δ1

(9)

βCx(t)表示C段翼中的x小段機翼撲動角函數，xC為C段翼的第x小段，nC表示C段翼共分為nC段，βC(t)表示C段翼末端處的撲動角函數。

2.2 扭轉函數

撲翼在上下拍動折疊的同時，也在進行扭轉運動，且大鳥實際拍動時，外部扭轉大，內部扭轉小。

(10)

(11)

f表示撲翼撲動頻率，φ表示扭轉滯后角，αx(t)表示第x小段撲翼的扭轉角，α(t)表示翼尖的扭轉角，n表示撲翼共分為n段。

考慮進急回特性后，上式中各翼段在各個時刻的撲動頻率分別為：

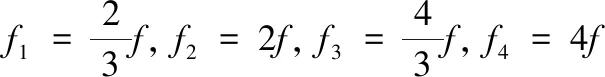
(12)

運動參數設置如表1所示。

表1 撲動參數設置

在XFLOW中按公式編寫程序，得一個周期內撲翼的拍動過程，如圖4所示。

3 數值仿真

3.1 仿真環境設置

本文選用XFlow軟件進行仿真，XFlow是基于玻爾茲曼方法的流體仿真軟件。XFlow采用無網格技術，由系統在后臺自動繪制網格，與Fluent[15]相比節省了大量繪制網格的時間。

將流場域設置為4 m×2 m×2 m的模擬風洞，y軸正方向指向撲翼飛行器正上方，流體速度指向x軸正方向，z軸正方向指向左翼翼展方向。計算域流體為空氣，且軟件仿真中無風動壁面和支撐系統對來流進行干擾。計算模型選用單相外部流絕熱模型，其他仿真參數設置如表2。

圖4 一周期內撲翼運動過程示意圖

表2 仿真參數設置

在計算域的設置中，還需要考慮風洞的阻塞比問題，即當風洞的阻塞比大于2%時，需要修正阻塞干擾產生的誤差。阻塞比設為δ：

δ=Sn/S

(13)

Sn為撲翼飛行器沿x軸正方向的投影面積,S為風洞氣流入口的面積，由XFlow導出模型參數可知，前者值為0.031 7 m2，后者值為4 m2，計算得阻塞比為0.79%，因此不需要進行對阻塞干擾的修正。

3.2 參數選擇

影響撲翼飛行器氣動特性的參數有很多，比如撲動頻率、機身迎角、內外翼折疊角等。本文主要研究撲翼飛行器的內外折疊角對飛行器氣動特性的影響，擬要研究的參數有折疊角個數、內外折疊角幅值、外折疊角的折疊位置(用C段翼的長度來表示)等。

其中，當沒有折疊角存在時(0折疊)，表示單段翼；當只有內折疊角存在，即為1個折疊角飛行(1折疊)，表示兩段翼；內外折疊角都存在，則為2個折疊角飛行(2折疊)，表示三段翼。本文采用控制變量法，設定多個研究參數，將其中一個參數設為變量進行對比分析，變量范圍設置如表3。

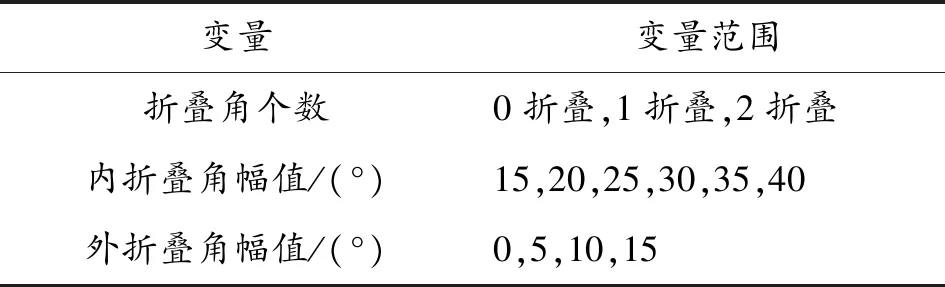
表3 變量范圍

4 仿真結果分析

在數值仿真中，內翼拍動幅值為60°，撲動頻率4 Hz，仿真時長1.5 s，按鴿子飛行速度，設置來流速度為10 m/s，計算時間步長為0.001 ms，幀頻率為100 Hz，并采用無量綱數平均升力系數Cl和推力系數Ct來衡量升力和推力。

對XFlow仿真出的數據進行處理，得到無折疊角的情況下，撲翼飛行器的平均升力系數為0.347，平均推力系數為0.902。

4.1 內外折疊角幅值對氣動特性的影響

從XFLOW中導出不同內外折疊角下升力系數與阻力系數的數據計算平均值，得圖5、圖6。

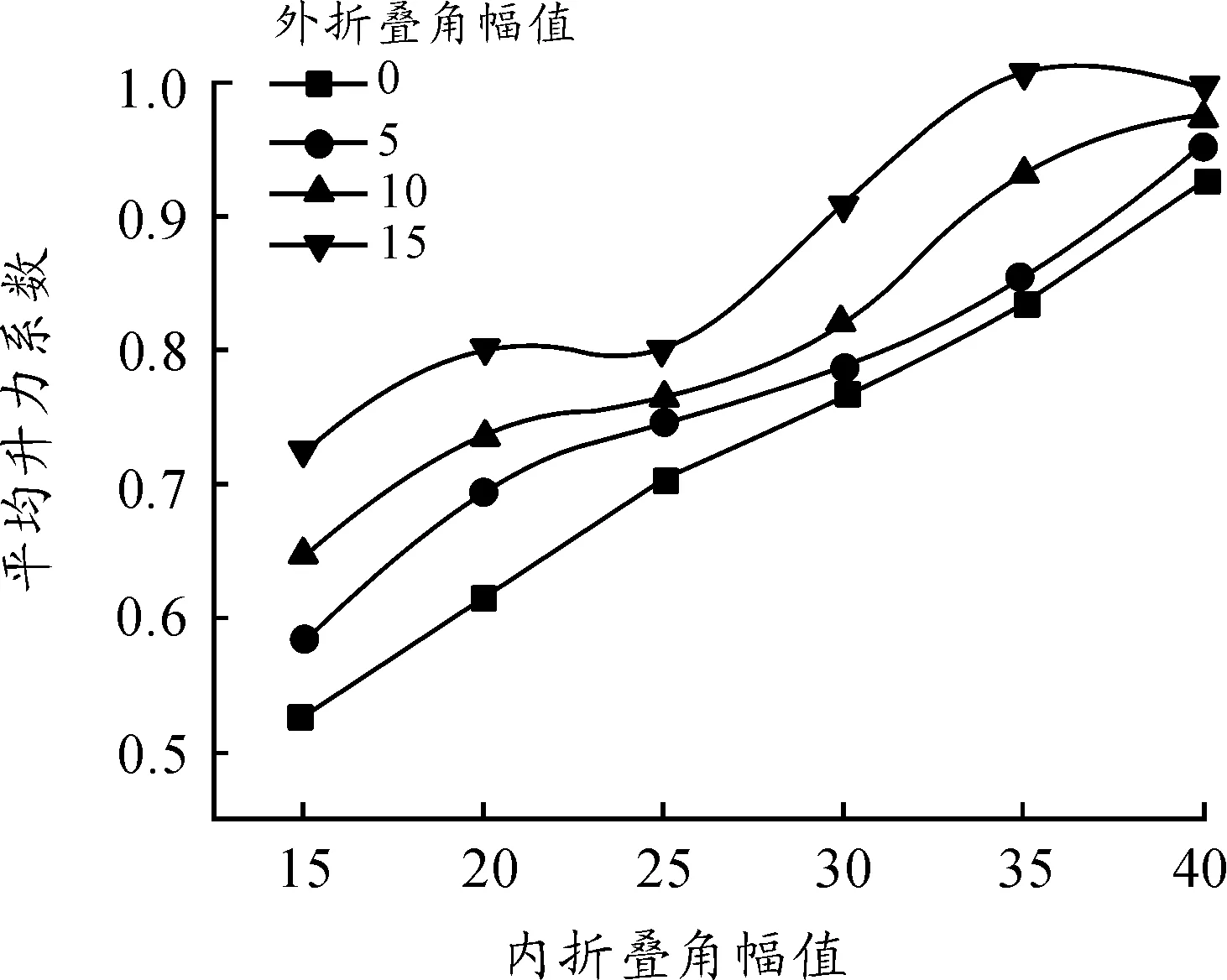
圖5 內外折疊角幅值對平均升力系數的影響曲線

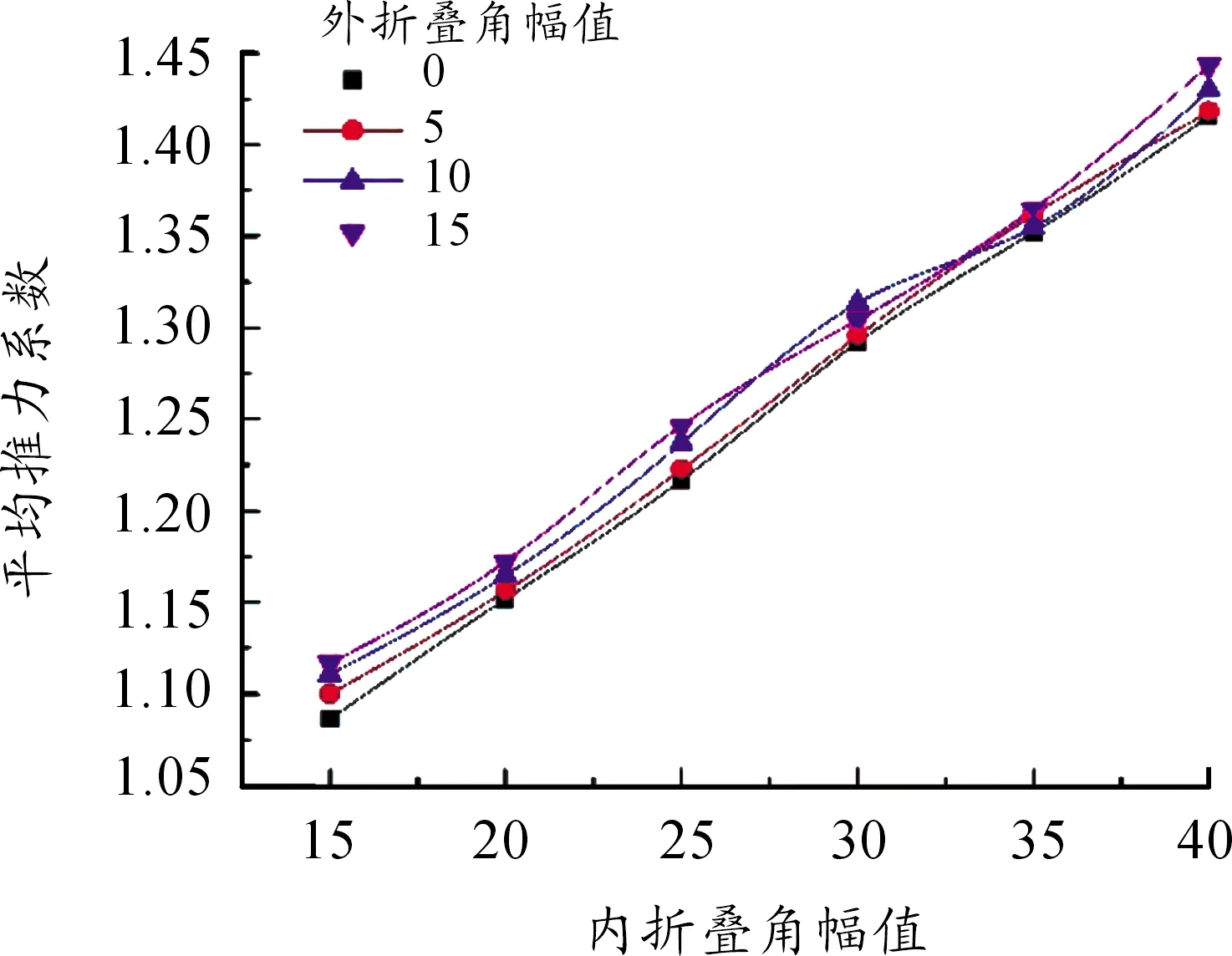
圖6 內外折疊角幅值對平均推力系數的影響曲線

首先是平均升力系數，當外折疊角幅值不變時，平均升力系數隨著內折疊角幅值的增加而增加，當內折疊角幅值不變時，平均升力系數也隨著外折疊角幅值的增加而增加。但當兩者聯合作用時，呈現出復雜的非線性增長關系，這種非線性會隨著外折疊角幅值的增加而更加明顯。

其次在平均推力系數方面，當外折疊角幅值不變時，平均推力系數隨內折疊角幅值的增加而增加，但當內折疊角幅值不變時，平均推力系數基本不會受到外折疊角幅值的影響。

因此推測：內折疊角是影響撲翼升力和推力的主要因素，而外折疊角進對推理幾乎無影響，對升力的影響遠小于內折疊角。

原因是：外折疊角幅值遠小于內折疊角，折疊過程對迎風面積的改變極小，故飛行器推力幾乎不變；但又因折疊作用，氣流加速繞過翼尖，產生壓力差，從而對升力有小幅增加。

4.2 與無折疊、單折疊飛行器的對比分析

從XFlow中導出0折疊、1折疊、2折疊的仿真數據，運用Origin繪制曲線，得圖7與圖8。

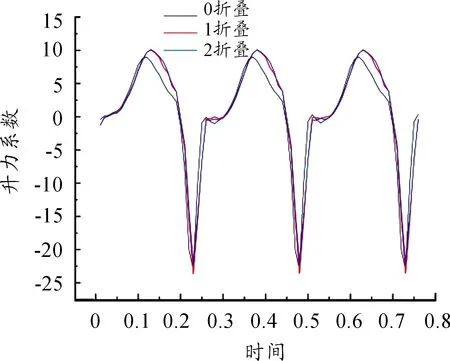
圖7 不同折疊角個數下的升力系數曲線

圖7中，下拍階段的正升力峰遠小于上拍階段的負升力峰，且下拍時，帶折疊角的升力峰大于無折疊角的升力峰，這是因為急回特性的作用，上拍階段所用時間僅占拍動周期的25%，上拍至最高處需要更高的拍動頻率，拍動頻率越高，產生的氣動力越大，因此負升力峰才會出現急劇的增加。

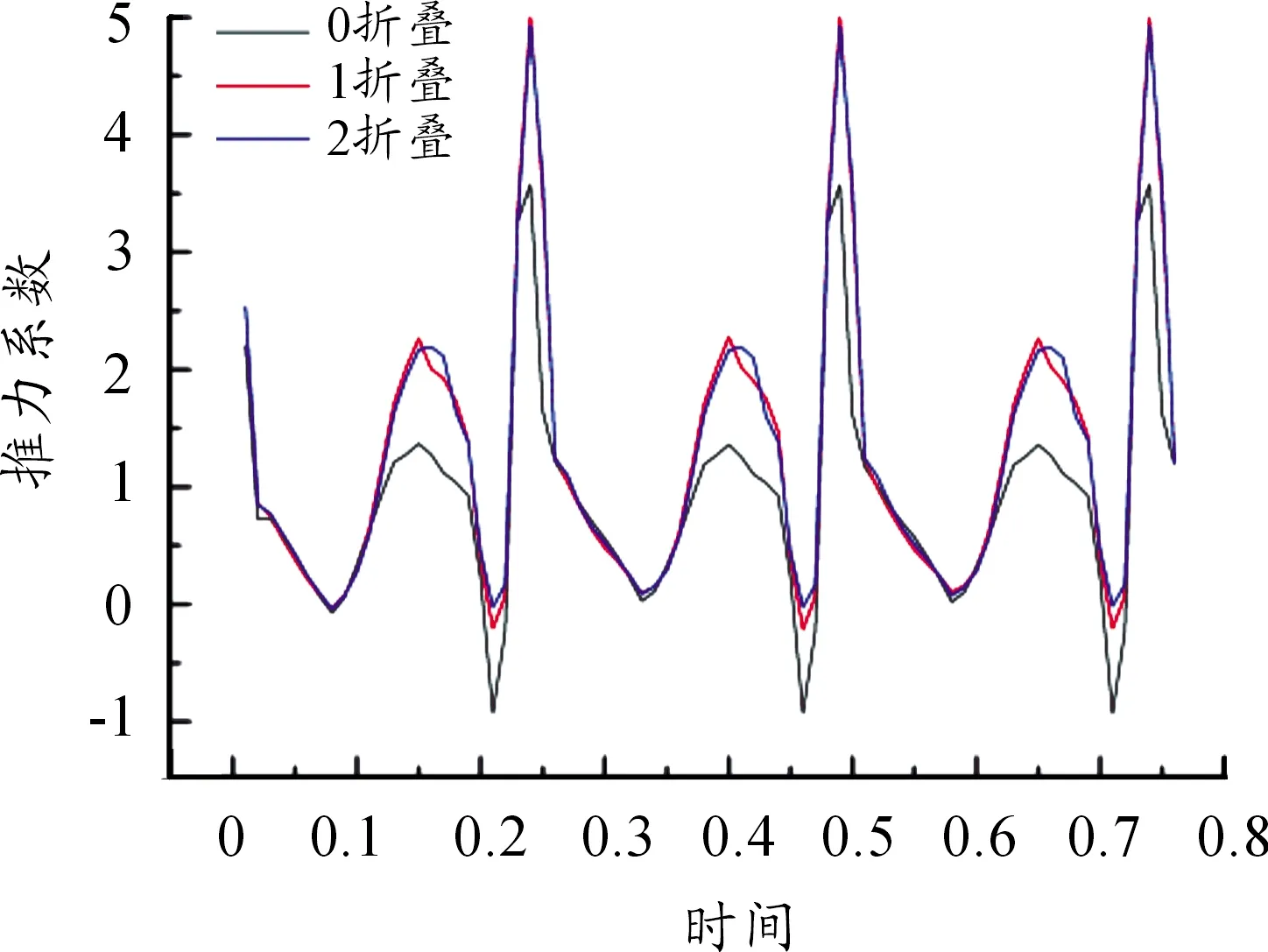
圖8 不同折疊角個數下的推力系數曲線

同理，在圖8中，下拍時的推力峰值，會因為折疊角的出現而又明顯的增益，但與 由翅膀的扭轉運動產生的，其方向指向飛行方向。而升力是由翅膀上下拍動產生，一個周期內升力有正有負，但總升力仍為正值。

觀察兩圖發現，帶折疊角的氣動特性遠優于無折疊角的撲翼模型，且在圖7、圖8中折疊角個數的影響幾乎分辨不出。結合1.1節對高速攝影的分析和4.1節中的推論，再次說明折疊角會增加撲翼飛行器的升力和推力，但不同折疊角下氣動力變化曲線接近一致，而均值不同，可見內折疊角在氣動力增益中起主要作用，而外折疊只能小幅增加飛行器的氣動力。

對推力幾乎無影響的原因是：翅膀在拍動過程中，外側羽毛會出現展向和弦向兩個方向的被動折疊，而本文所建的簡化模型主要研究展向折疊現象，未考慮外側羽毛的弦向扭轉(圖9展示羽毛的弦向扭轉過程)。按照翅膀上下拍動時，氣流產生升力，前后扭轉時，氣流產生推力的飛行機理，故此推測羽毛的展向折疊影響升力，弦向扭轉影響推力。但該推測是否成立，需要進一步的研究論證。

圖9 外側羽毛的弦向扭轉

4.3 各翼段所受氣動力矩

從XFlow中導出右翼A、B、C三段翼各自的升力力矩Ml和推力力矩Mt數據，得圖10與圖11。其中力矩的葉素法計算公式如下：

(14)

(15)

圖10和圖11中，各翼段的升力力矩和推力力矩也呈周期性變化，且因急回特性，負力矩峰值大于正力矩峰。另B段翼的升力力矩和阻力力矩都是最大的，這是因為B段翼拍動時的受力面積最大，經葉素法的積分值最大。

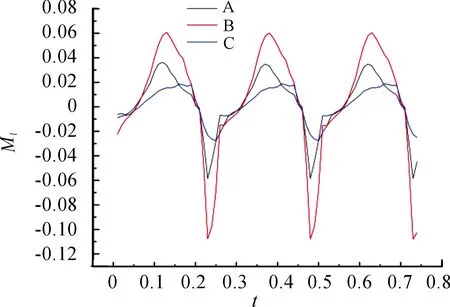
圖10 各翼段升力力矩變化曲線

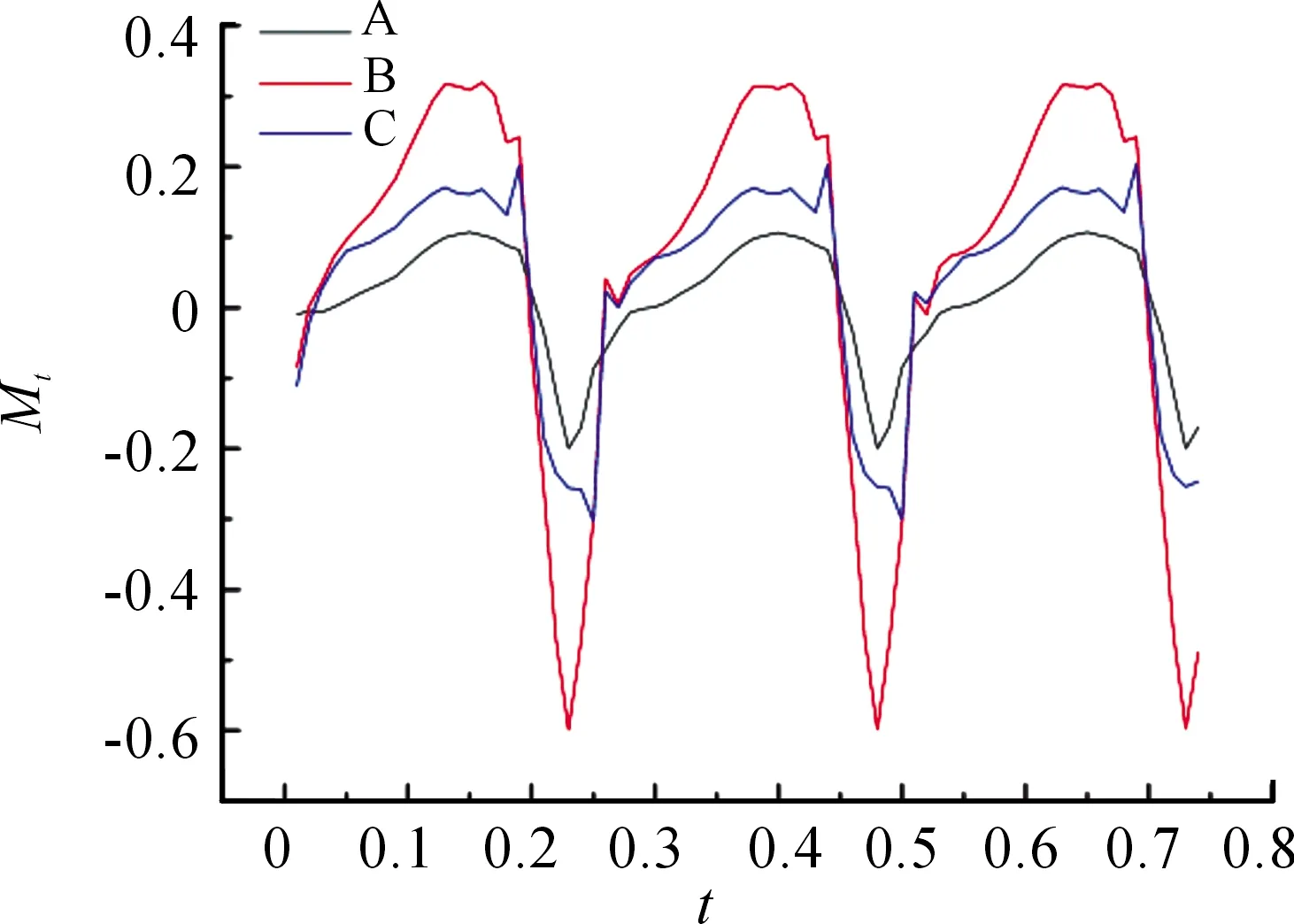
圖11 各翼段推力力矩變化曲線

結合式(13)和式(14)可知，翅膀拍動產生氣動力有著周期性的變化規律，其中B段翼，也就是外翼，是產生氣動力矩的主要部位。

5 結論

1) 內折疊角可明顯增加撲翼飛行器的升力和推力，但外折疊角卻只能小幅增加飛行器升力，對推力幾乎無影響。

2) 升力和推力都呈現出周期性變化，且因為急回特性的存在，上拍階段的升力峰和推力峰都會大于下拍階段的峰值，這也說明氣動力的大小與拍動頻率呈正比。帶折疊角撲翼的升力和推力會明顯高于無折疊角撲翼，不同折疊角數目下的曲線卻十分接近，再次說明內折疊角是改變氣動力的主要因素。

3) 觀察各翼段的升力矩和推力矩發現：氣動力矩呈周期性變化，且負力矩峰大于正力矩峰，外翼是撲翼產生氣動力和氣動力矩的主要部位。