一類捕食-食餌模型正解的存在唯一性與穩(wěn)定性

楊夢(mèng)娜, 李艷玲

(陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，西安 710119)

1 引言

具有Holling-III 型功能反應(yīng)函數(shù)的捕食-食餌模型作為一類重要的生物模型，得到了國(guó)內(nèi)外很多學(xué)者的關(guān)注[1-6].其中文獻(xiàn)[1]使用迭代方法和構(gòu)造相關(guān)序列研究了一類具有Holling-III 型反應(yīng)函數(shù)的捕食-食餌模型，得到了正常數(shù)平衡解的全局漸近穩(wěn)定性；文獻(xiàn)[2]利用錐上不動(dòng)點(diǎn)理論和線性穩(wěn)定性理論研究了一類具有Holling-III 型非線性密度制約的捕食-食餌模型，得到了正解的存在性與穩(wěn)定性；文獻(xiàn)[4]利用分歧理論、隱函數(shù)定理以及攝動(dòng)技巧研究了一類具有非單調(diào)生長(zhǎng)率且功能反應(yīng)函數(shù)為Holling-III 型的捕食-食餌模型，得到了其正解在一維情形下的存在性及穩(wěn)定性.本文是在文獻(xiàn)[4]的基礎(chǔ)上，進(jìn)一步研究如下的捕食-食餌模型

本文主要利用不動(dòng)點(diǎn)指標(biāo)理論和擾動(dòng)理論研究問(wèn)題(2)在N 維情形下正解的存在唯一性與穩(wěn)定性.

2 預(yù)備知識(shí)

本節(jié)首先給出一些基本的定義和引理，其次運(yùn)用極值原理和上下解方法得到問(wèn)題(2)正解的先驗(yàn)估計(jì)和正解存在的一些必要條件.

如果問(wèn)題(2)的一個(gè)解滿足對(duì)任意的x ∈?, u(x) ＞0 且v(x) ＞0，則稱(u,v)為問(wèn)題(2)的一個(gè)正解.

設(shè)q(x)∈Cα(?)(0 ＜α ＜1), λ1(q)為如下特征值問(wèn)題

的主特征值.由文獻(xiàn)[9]可知，λ1(q(x))連續(xù)依賴于q(x)，且λ1(q(x))是簡(jiǎn)單的.另外，λ1(q(x))是關(guān)于q(x)的遞增函數(shù).為了簡(jiǎn)單起見，定義λ1(0) = λ1，對(duì)應(yīng)的特征函數(shù)記為φ1，且φ1＞0, x ∈?.

考慮以下非線性邊值問(wèn)題

和

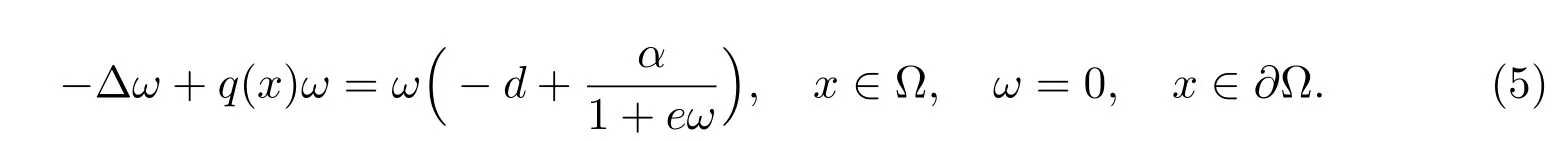
由文獻(xiàn)[10]可知，若a ≤λ1，則問(wèn)題(4)只有平凡解u = 0；若a ＞λ1，則問(wèn)題(4)存在唯一正解，記為θa.特別地，θa＜a 且連續(xù)依賴于a.由文獻(xiàn)[4]可知，若α ?d ＞λ1(q(x))，則問(wèn)題(5)存在唯一正解，記為θα,d(q)，并簡(jiǎn)記θα,d(0) = θα,d.因此，在一定條件下，問(wèn)題(2)存在半平凡解(?u,0)及(0,?v)，其中?u=θa, ?v =θ1,d.

1) 若F′(y)具有α 性質(zhì)，則indexW(F,y)=0；

2) 若F′(y)沒(méi)有α 性質(zhì)，則indexW(F,y)=(?1)β，其中β 是F′(y)的所有大于1 的特征值的代數(shù)重?cái)?shù)之和.

引理2[11]令q(x) ∈Cα()(0 ＜α ＜1)，M 為正常數(shù)，使得對(duì)任意的x ∈, ?q(x)+M ＞0，則以下結(jié)論成立：

1) λ1(q(x))＜0 ?r[(?△+M)?1(?q(x)+M)]＞1；

2) λ1(q(x))＞0 ?r[(?△+M)?1(?q(x)+M)]＜1；

3) λ1(q(x))=0 ?r[(?△+M)?1(?q(x)+M)]=1；其中r[(?△+M)?1(?q(x)+M)]為算子(?△+M)?1(?q(x)+M)的譜半徑.

引理3如果(u,v)為問(wèn)題(2)的正解，則

證明 假設(shè)(u,v)為問(wèn)題(2)的正解，從關(guān)于u 的方程可以得到

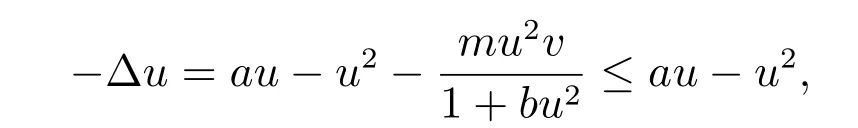
因此?u 可以作為下述問(wèn)題

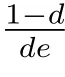
令z =cu+mv，結(jié)合u 和v 的方程，則z 滿足

由極大值原理可知

又由于z =cu+mv，從而

引理4如果問(wèn)題(2)存在正解，則

證明 設(shè)(u,v)是問(wèn)題(2)的正解，則

對(duì)上式兩端同時(shí)乘以u(píng)，再在? 上積分，運(yùn)用格林公式，則

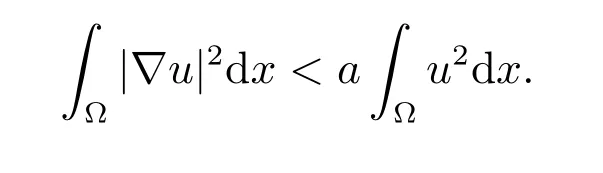
又由Poincar′e 不等式可知

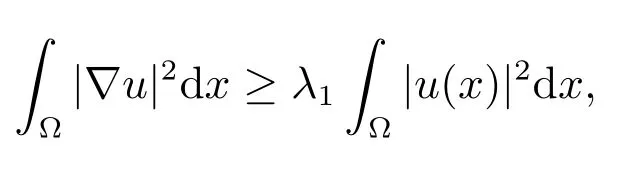
從而a ＞λ1.

從v 的方程中，可以得到

因此

3 正解的存在性

本節(jié)主要利用不動(dòng)點(diǎn)指標(biāo)理論[2,12]研究問(wèn)題(2)正解的存在性.為了計(jì)算不動(dòng)點(diǎn)指標(biāo)，引入以下記號(hào)：

則通過(guò)計(jì)算得到：

取M 充分大，使得(u,v)∈D 時(shí)

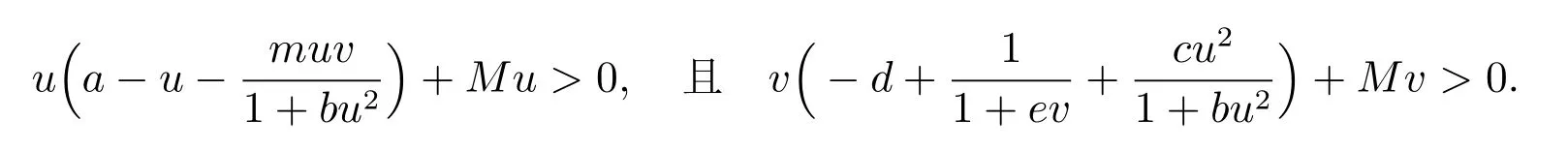
定義算子F: E →E:

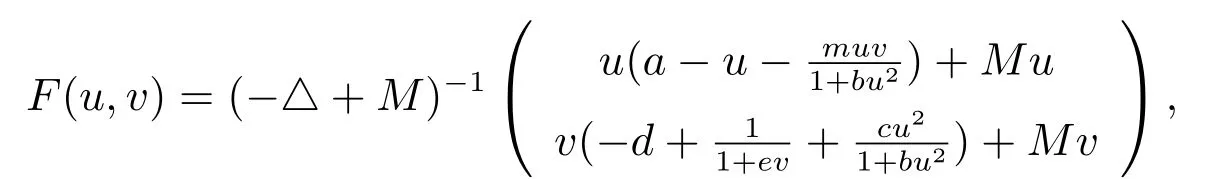
則F :D →W 是緊算子，則問(wèn)題(2)有解等價(jià)于算子方程F(u,v)=(u,v)有解.

對(duì)于任意的t ∈[0,1]，定義

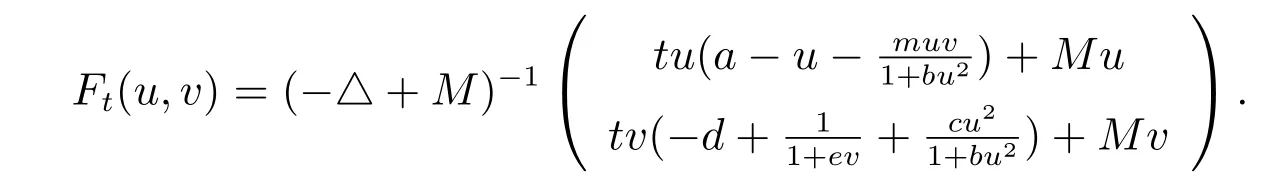
引理5假設(shè)a ＞λ1，則有：

1) degW(I ?F,D)=1；

2) 若?d+1 ?=λ1，則indexW(F,(0,0))=0；

證明 1) 由引理3 知，F(xiàn) 在?D 上沒(méi)有不動(dòng)點(diǎn)，因此degW(I ?F,D)有意義，對(duì)于任意的t ∈[0,1]，F(xiàn)t的不動(dòng)點(diǎn)為下述方程的解

則對(duì)于任意的t ∈[0,1]，F(xiàn)t的不動(dòng)點(diǎn)滿足u ≤a, v ≤R.因此Ft的不動(dòng)點(diǎn)一定落在D 內(nèi)，再由度的同輪不變性知，degW(I ?Ft,D)不依賴于t，于是

degW(I ?F,D)=degW(I ?F0,D)=degW(I ?Ft,D).

當(dāng)t=0 時(shí)，問(wèn)題(7)只有平凡解(0,0)，所以degW(I?F0,D)=indexW(F0,(0,0)).注意到

記

由引理1 知，indexW(F0,(0,0))=1，因此degW(I ?F,D)=1.

如果ξ ＞0，則a = λ1，這與已知相矛盾.因此ξ ≡0，同理可證η ≡0.從而I ?F′(0,0)在(0,0)上可逆.

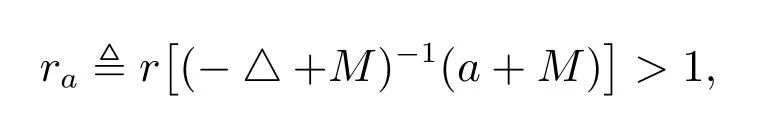
又由于a ＞λ1，則同時(shí)ra為算子(?△+M)?1(a+M)的主特征值，對(duì)應(yīng)的特征函數(shù)φ ＞0，取t0= r?1a，則0 ＜t0＜1，并且(I ?t0F′(0,0))(φ,0)=(0,0)∈S(0,0)，因此F′(0,0)具有α 性質(zhì)，從而由引理1 知，indexW(F,(0,0))=0.

3) 通過(guò)計(jì)算得到

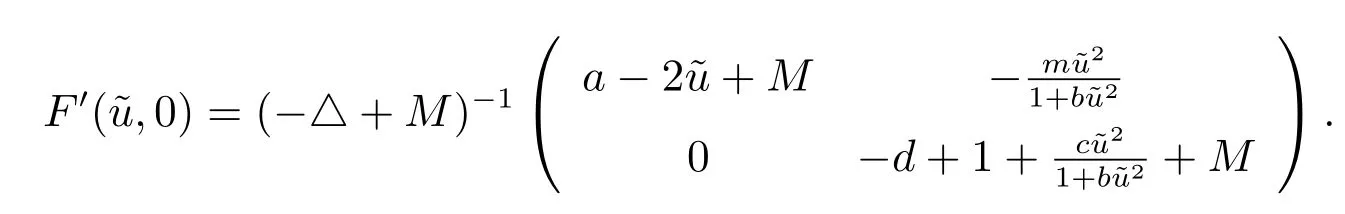
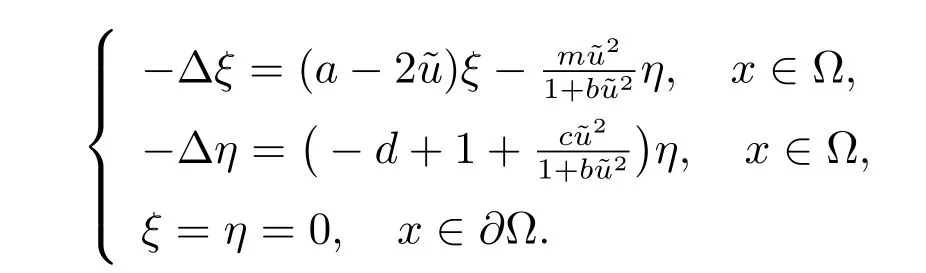
若η ?≡0，則由η ∈K 知

記

由于

從而由引理2 可知，r(A) ＞1 且是算子A 的主特征值，相應(yīng)的特征函數(shù)φ ＞0，取t0=r?1(A)，則0 ＜t0＜1, (0,φ)∈(u?,0)S(u?,0)，并且

因此F′(u?,0)在W(u?,0)上具有α 性質(zhì)，從而由引理1 知，indexW(F,(u?,0))=0.

4) 由上節(jié)可知，當(dāng)

時(shí)，I ?F′(u?,0)在(u?,0)上可逆.由于

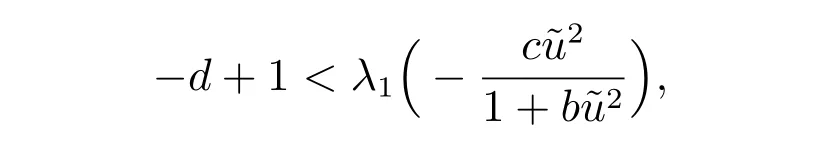
從而r(A) ＜1.假設(shè)F′(u?,0)在(u?,0)上具有α 性質(zhì)，則存在0 ＜t ＜1, (φ1,φ2) ∈(u?,0)S(u?,0)，使得

于是

又由于φ2∈K{0}.從而為算子A 的一個(gè)特征值，這與r(A) ＜1 相矛盾.因此F′(u?,0)在W(u?,0)上不具有α 性質(zhì)，根據(jù)引理1 可知，indexW(F,(u?,0)) = (?1)β，其中β 是F′(u?,0)的所有大于1 的特征值的代數(shù)重?cái)?shù)之和.

即

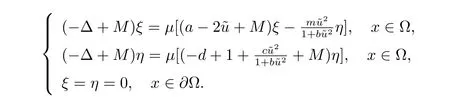
如果η ?≡0，則

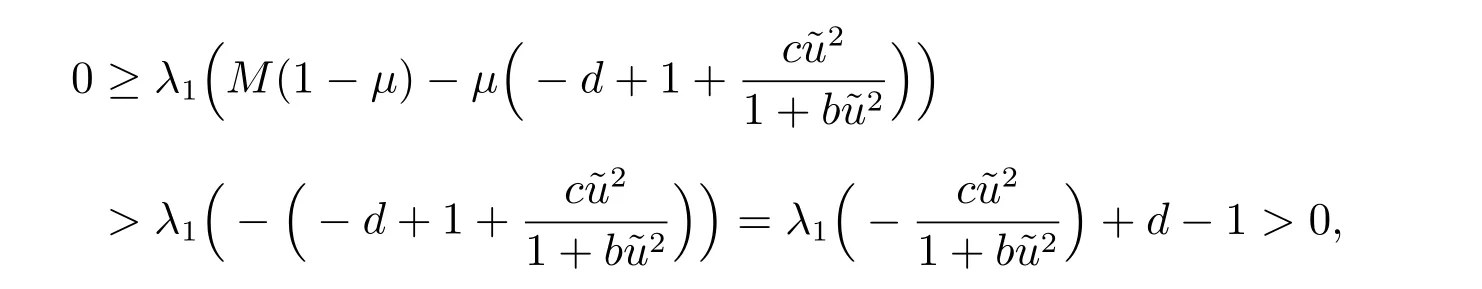
從而矛盾，因此η ≡0.

若ξ ?≡0，則

從而矛盾.因此F′(?u,0)沒(méi)有比1 大的特征值.于是根據(jù)引理1 得indexW(F,(?u,0))=1.

類似引理5，我們可以證明如下結(jié)論：

引理6設(shè)?d+1 ＞λ1，則：

1) 若a ＞λ1時(shí)，則indexW(F,(0,?v))=0；

2) 若a ＜λ1時(shí)，則indexW(F,(0,?v))=1.

從而由引理5 和引理6，以及度的可加性得到問(wèn)題(2)正解的存在性定理.

定理11) 如果?d+1 ＞λ1, a ＞λ1時(shí)，則問(wèn)題(2)除(0,0), (?u,0), (0,?v)之外，至少還有一個(gè)正解；

2) 如果?d+1 ＜λ1，則問(wèn)題(2)存在正解當(dāng)且僅當(dāng)

證明 1) 根據(jù)引理6 和引理7 可以得到

1=degW(I ?F,D)=indexW(F,(0,0))+indexW(F,(?u,0))+indexW(F,(0,?v))=0,從而矛盾，因此問(wèn)題(2)至少還有一個(gè)正解.

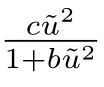
從而矛盾，因此問(wèn)題(2)至少有一個(gè)正解.

4 正解的唯一性與穩(wěn)定性

本節(jié)主要運(yùn)用度的可加性質(zhì)和線性算子的擾動(dòng)技巧[14-16]來(lái)討論當(dāng)參數(shù)m 充分小時(shí)，問(wèn)題(2)正解的唯一性與穩(wěn)定性.

首先考慮下述方程

引理7設(shè)

則當(dāng)m ＞0 且趨于0 時(shí)，問(wèn)題(2)的任意正解都是非退化且線性穩(wěn)定的.

證明 采用反證法來(lái)證明.假設(shè)存在mi→0，使得問(wèn)題(2)在m = mi時(shí)的正解(ui,vi)是退化的或者線性不穩(wěn)定的，則存在(ξi,ηi)?≡(0,0)，使得如下線性化問(wèn)題的特征值μi滿足Re(μi)≤0，不妨設(shè)‖ξi‖2+‖ηi‖2=1.

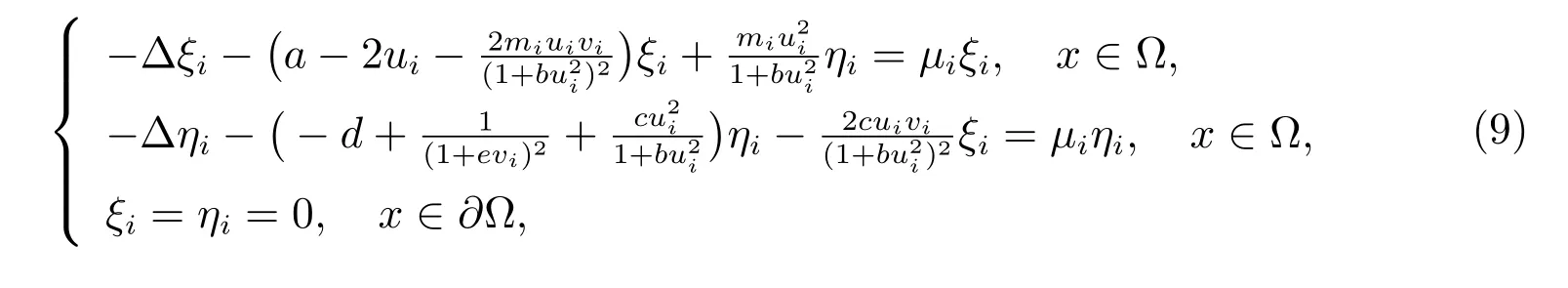
顯然，當(dāng)mi→0 時(shí)，(ui,vi) →(?u,v?).記ˉξi和ˉηi分別是ξi和ηi的共軛算子，對(duì)(9)式的第一個(gè)方程乘以ˉξi，第二個(gè)方程乘以ˉηi，然后在? 上積分，最后兩者相加得到

由引理3 知，ui和vi都有界，所以Re(μi)和Im(μi)有界，因此μi有界.可設(shè)μi→μ，則Re(μ)≤0.又由Lp估計(jì)和Sobolev 嵌入定理可得，ξi和ηi有界，設(shè)ξi→ξ, ηi→η.

再對(duì)(9)式兩端關(guān)于i 取極限，得到

若ξ ?≡0，則算子?△?(a ?2?u)I 的特征值全大于0，因此μ ≥λ1(?a+2?u) ＞0，從而與Re(μ)≤0 相矛盾，因此ξ ≡0.

若η ?≡0，將ξ =0 代入(10)式中第二個(gè)方程，則

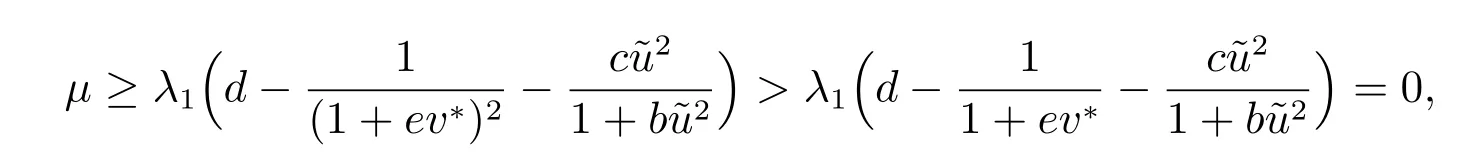
從而與Re(μ)≤0 相矛盾，因此η ≡0.

所以問(wèn)題(9)的所有特征值的實(shí)部都大于0，這意味著問(wèn)題(2)的正解是非退化的且線性穩(wěn)定的.

定理2設(shè)

則當(dāng)m ＞0 且充分小時(shí)，問(wèn)題(2)有唯一正解，而且是非退化和線性穩(wěn)定的.

證明 由定理1 和引理7 可知問(wèn)題(2)存在正解，而且是非退化和線性穩(wěn)定的，故只需要證明正解的唯一性即可.首先容易驗(yàn)證平凡解和半平凡解都遠(yuǎn)離正解，再根據(jù)緊性理論可知問(wèn)題(2)至多有有限個(gè)正解，記為{(ui,vi) : i = 1,2,··· ,l}.又由引理7 可知，indexW(F,(ui,vi))=1.結(jié)合度的可加性及引理6 可得

因此問(wèn)題(2)只有一個(gè)正解，而且是非退化和線性穩(wěn)定的.

5 數(shù)值模擬

這節(jié)主要討論系統(tǒng)(1)對(duì)應(yīng)的一維空間的情形，即

利用Matlab 工具做數(shù)值模擬，根據(jù)直觀圖像來(lái)驗(yàn)證前面研究得到的理論結(jié)果，通過(guò)計(jì)算可得λ1=.

首先，根據(jù)定理1 的條件進(jìn)行數(shù)值模擬，參數(shù)取值分別為a = 0.65, b = 1, c =1, d = 0.4, e = 1.25 和m = 0.5.圖1 驗(yàn)證了系統(tǒng)(1)在一維情形下正解的存在性，這與定理1 的結(jié)論一致，這說(shuō)明兩物種在定理1 的條件下，食餌和捕食者可以共存.并且隨著時(shí)間t 的增大，可以看出兩物種趨于穩(wěn)定.

圖1: 系統(tǒng)(11)的正解(u(x,t),v(x,t))的模擬圖，其中圖(a)和圖(b)分別為正解(u(x,t),v(x,t))的模擬圖；圖(c)為正解(u(x,t),v(x,t))在T =100 時(shí)刻的剖面圖；圖(d)為任意時(shí)刻正解(u(x,t),v(x,t))在(0,2π)上的L1 范數(shù)

其次，圖2 分別驗(yàn)證了當(dāng)食餌種群的生長(zhǎng)率充分小時(shí)，或者捕食者種群的死亡率充分大時(shí)，食餌和捕食者不能共存；除此以外，當(dāng)食餌種群的生長(zhǎng)率充分小且捕食者種群的死亡率充分大時(shí)，食餌和捕食者也不能共存，這些符合引理4 的結(jié)論.

下面給出一個(gè)二維空間的例子，驗(yàn)證定理1 的結(jié)論.

這里取a=0.65, b=1, c=1, d=0.4, e=1.25, m=0.5 和t=4，從圖3 中可以看出，系統(tǒng)(12)的正平衡態(tài)解的存在，這說(shuō)明兩物種可以共存.從圖4 可以看出，隨著時(shí)間t 的增大，兩物種趨于穩(wěn)定.

圖3: 系統(tǒng)(12)在t=4 時(shí)刻(u(x,y,t),v(x,y,t))的模擬圖，其中圖(a)和圖(b)分別為正解(u(x,y,t),v(x,y,t))的投影圖；圖(c)和圖(d)分別為正解(u(x,y,t),v(x,y,t))的模擬圖

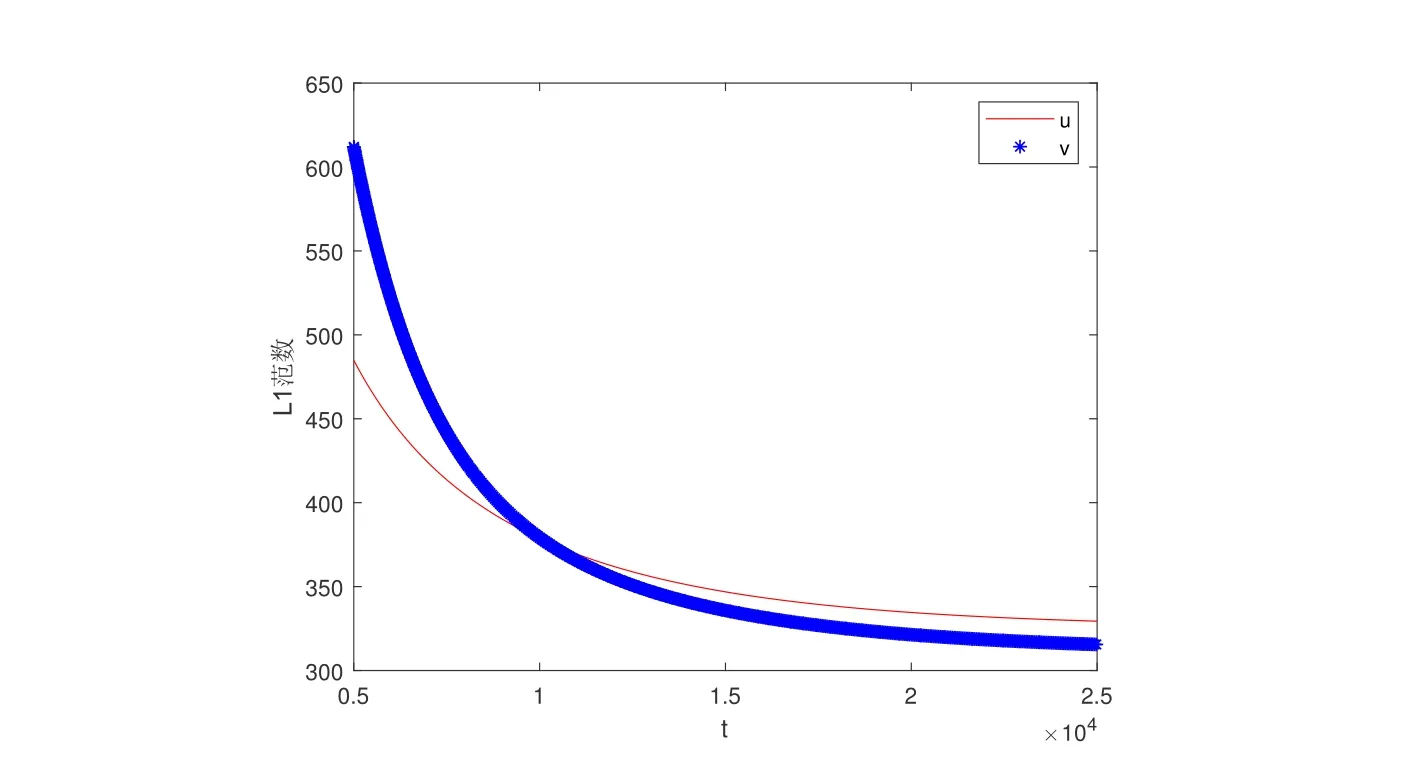
圖4: 系統(tǒng)(12)的正解(u(x,y,t),v(x,y,t))在(0,2π)×(0,2π)上的L1 范數(shù)