機器學習方法在中醫證候分析中的應用

張龍 王國明

摘要：傳統的中醫辨證診療主要基于“望、聞、問、切”得到的四診信息，由于摻雜過多的醫師主觀因素，即使對同一個病人的辨證結果也可能不盡相同，因此如何建立一個科學而規范化的中醫證候的量化標準是一個值得研究的課題。本文將機器學習中的層次聚類和因子分析方法應用于中醫證候量化分析，通過對采集到的1499例典型高血壓病例的處理與分析，實驗結果表明，機器學習方法可以有效地挖掘中醫證候中隱藏的信息，為中醫輔助診療提供重要的途徑。

關鍵詞：機器學習;因子分析;層次聚米;數據挖掘;證候扮析

中圖分類號：TP391 文獻標識碼：A

文章編號：1009-3044（2020）14-0001 1-03

層次聚類算法出現于1963年，其指導思想是對給定的待聚類數據集合進行層次化分解。因子分析最早出現于1904年英國統計學家斯皮爾曼（C.Spearman），最初應用于心理學與教育學中，其主要目的是對顯在變量找出其潛在變量（因子），用少數的潛在變量來揭示相互之間有關系的顯在變量，將具有相同本質的變量歸納為一個因子。

聚類分析在中醫領域有諸多的應用，如阮雪萍等人將聚類分析應用于探究阻塞性睡眠呼吸與血清SOD、MDA的相關性研究;鐘小雪等人提出基于聚類分析的中醫癥候的研究。因子分析同樣高頻率的出現在中醫的應用中，如李亮亮等人基于因子分析對中醫證素辨證研究。而本文以高血壓病例為例，探索基于聚類分析和因子分析在中醫證候中的應用。

1層次聚類算法

1.1數據來源

本文的數據是來源于全國五所醫院中提取的1499份高血壓患者的四診信息，將篩選過后符合標準的四診信息進行編碼。

1.2基本思想與算法流程圖

1.2.1基本思想

層次聚類法是使用比較廣泛的一種方法，這種方法首先把多個變量各自看作為一個類簇，根據兩個類之間的相似性統計量，把兩個最接近的類簇合并成一個新的類簇，計算新的類簇和其他各類簇間的相似性統計量，再選擇最接近的兩個類簇合并成一個新的類簇，直到達到設定的分類數目為止。相似性統計量通常是以距離為相似性統計指標常用的指標有歐式距離、重心法、最長距離法、離差平方和法（Ward法）。本文是基于離差平方和法進行兩個類簇之間距離的計算，其主要是基于方差分析的思想，如果分類正確那么同類簇的樣品之間的離差平方和較小，類簇與類簇之間的離差平方和較大。

1.2.2算法流程圖

1.3實驗結果

實驗是將篩選過后的四診信息變量進行聚類。使用R語言的hclustf）函數或者SPSS軟件都可以畫出聚類圖。聚類結果如下圖2所示。

1.4層次聚類實驗結論

由于聚類分析是無監督學習，在分類過程中，它能自動的將樣本進行歸類處理，減少了主觀判斷造成的分析誤差，使得分類的結果更加具有客觀性和科學性。但同時我們也意識到對于中醫這種專業性比較強的領域，在部分聚類分析的結果中，可能會出現沒有臨床癥狀的四診信息會被聚為一類，也有可能出現并無關聯甚至相互矛盾的癥狀被聚為一類。而因子分析作為一類降維的相關分析技術，其主要目的是從多個變量中找出因子，以少數幾個因子解釋一群具有相互關系的變量，因其能夠根據權重反映變量自身的重要程度，提高綜合評價的效率，近些年來被廣泛應用于社會學、管理學、經濟學等領域中。

2因子分析

2.1基本思想

探索性因子分析（Exploratory Factor Analysis，EFA）可在許多變量中找出隱藏的具有代表性的因子，將相同本質的變量歸入一個因子，從而減少變量的數目，還可檢驗變量間關系的假設。通常探索性因子分析是以協方差為基礎來估計其方程的參數，這就要求數據是連續的并且服從正態分布。但是中醫中收集到的四診信息通常是等級資料，無法滿足因子分析的潛在變量和顯在變量均為連續變量的前提條件。因此利用基于協方差系數矩陣的因子分析方法對收集到的四診信息進行分析，可能會出現錯誤的結果。Muthen后來提出了將等級資料變換為潛在連續變量，求得連續變量間多項相關系數，以多項相關系數進行探索性因子分析。本文采用基于多項相關系數矩陣的探索性因子分析和基于協方差矩陣下的探索性因子分析進行比較研究。

2.2數據建模

2.2.1協方差系數矩陣下的因子分析建模

2.3.1因子可行性分析

在對數據進行因子分析時，需要檢驗數據間是否存在一定的相關性，如果不存在相關性，則對該數據進行因子分析則毫無意義。進行可行性分析常用的方法有KMO系數與Bartlett卡方檢驗。

從表1的檢驗結果來看，KMO值等于0.832，接近于1，說明所有變量之間的簡單相關系數平方和遠大于偏相關系數平方和，因此適合于作因子分析;此外，從Bartlett球形檢驗的結果也可以發現，其相伴概率幾乎等于零，遠小于顯著性水平，則拒絕原假設，說明原始相關系數矩陣不可能是單位陣，即原變量之間存在相關性，適宜作因子分析。

2.3.2確定公因子個數

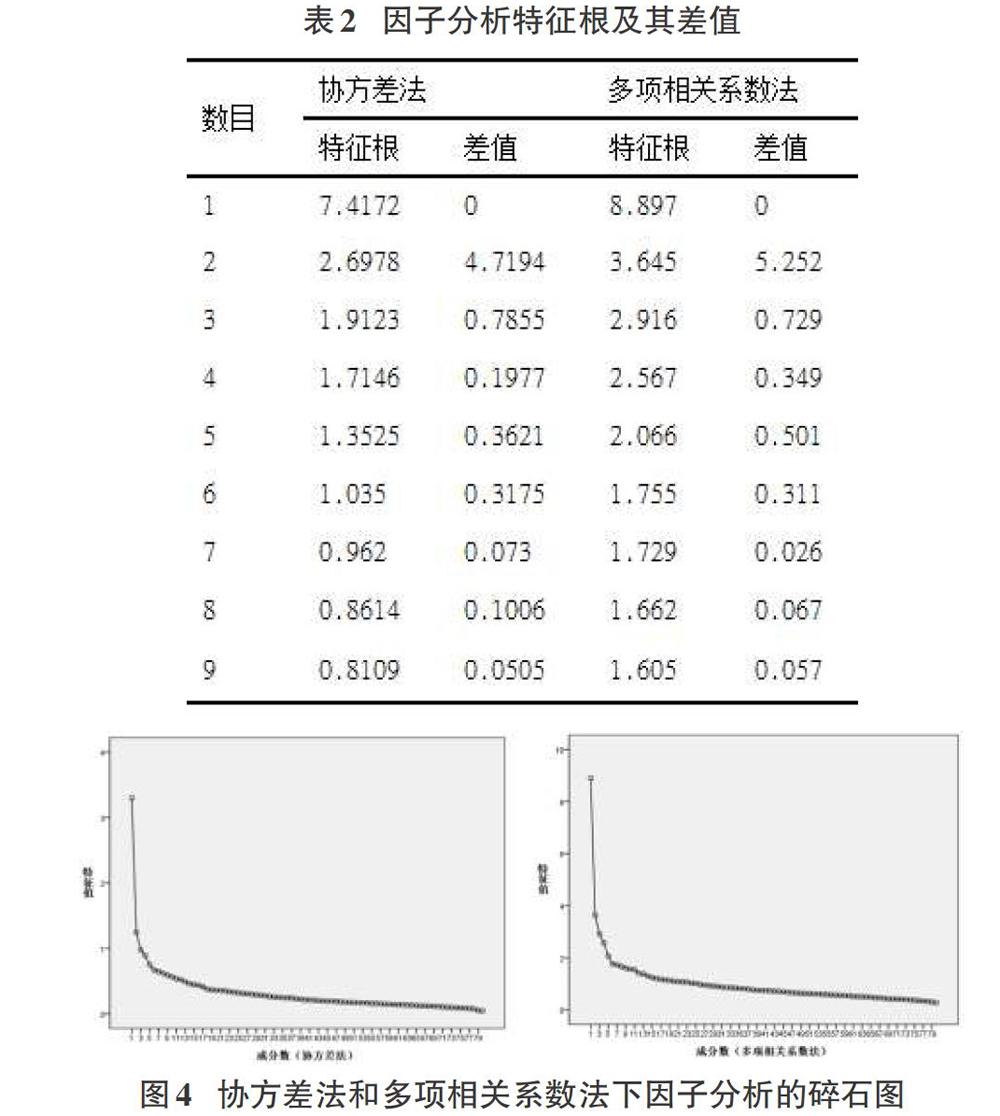
通常情況下，探索性因子分析中所提取的因子數量主要由特征根、方差累計貢獻率以及碎石圖等來決定。其中所提取因子的特征根一般要求大于1，且累計方差貢獻率要達到80%以上才能保證因子具有較強的解釋力度，但由于本文中數據的變量個數過多，因此需要結合特征根及其差值（表2）以及碎石圖（圖4）來選取因子。

首先從特征根及其差值（表2）來看，基于協方差矩陣的因子分析法和基于多項相關系數矩陣的因子分析法所提取的前5個因子的特征根都是大于1的，并且其差值相對較大，從第6個因子開始，特征根的差值逐漸變小，因此我們可以考慮選取5個因子。此外，從圖4的兩種因子分析方法下的碎石圖來看，都是在第6個因子處具有一個明顯的拐點，第6個因子開始趨于平滑曲線，這與特征根及其差值的結論相一致，即兩種方法對于所提取的因子數目沒有太大差別，都是提取5個因子較為適宜。

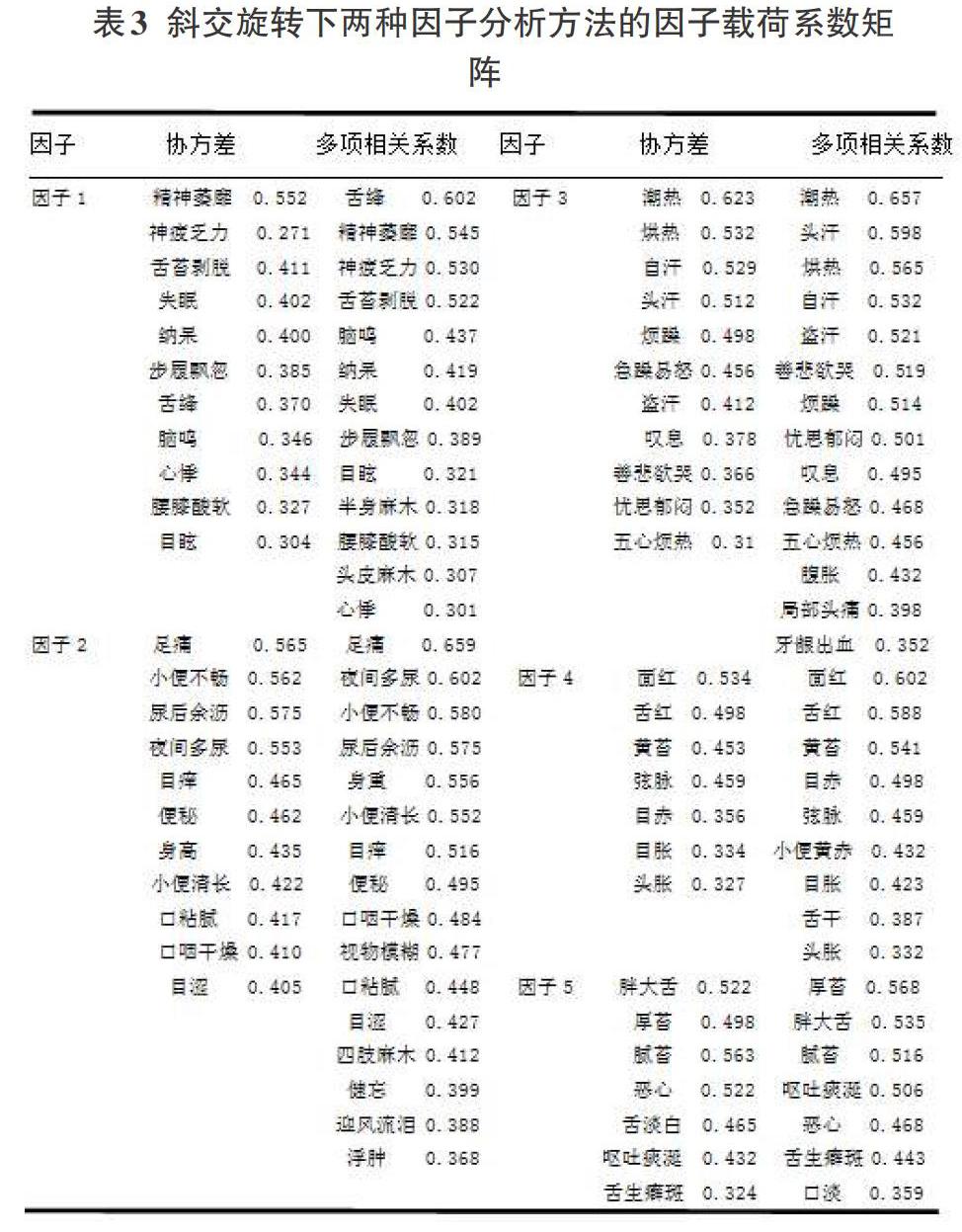
2.3.3結果（見表3）

2.4因子分析實驗結論

從因子載荷系數矩陣整體來看，兩種方法所提取的五個因子都存在其相對應的中醫證候。從每個因子所對應的中醫證候的載荷系數大小來看，基于多項相關系數矩陣的因子分析法更為精確、細化，并且載荷系數普遍高于基于協方差矩陣的因子分析方法下的載荷系數.這說明，如果取載荷系數較大時，基于協方差矩陣的因子分析方法極易忽略一部分變量，從而造成一定的分析誤差。綜上，使用基于多項相關系數矩陣的探索性因子分析方法所得到的結果更為合理可靠。