動態精密單點定位在鐵路勘測上的應用研究

董穎略

摘 要：利用2020年實測雙頻GNSS觀測數據，對動態精密單點定位的精度進行驗證和評估。與后處理差分軟件進行比較，結果顯示動態精密單點定位在每個方向上均能獲取厘米級的定位準度，其主要偏差體現在高程方向;同時衛星幾何空間分布極大的影響動態精密單點定位的結果，相比單一的GPS系統，融合GLONASS的觀測數據能較大的改善該問題。通過對上述結果進行分析得出動態精密單點定位可以在鐵路勘測等領域進行推廣應用。

關鍵詞：動態精密單點定位;GNSS精度;GPS+GLONASS雙系統

0引言

隨著測繪科學的發展，大量的先進儀器和技術應用到鐵路勘測、施工和監測的應用中。GNSS作為新興的測繪技術在鐵路測繪事業中得到了廣泛的應用[1]。其中RTK技術由于操作效率和可靠性較高等優點，在地形圖測繪、施工放樣等領域受到了青睞[2]。但RTK技術的應用需要與基準站同時進行觀測，并攜帶電臺發射改正數，這便大大限制了其工作范圍。而且在部分高山峽谷地帶，RTK技術不能正常工作[3]。精密單點定位技術的出現有望解決這一問題[4]。靜態精密單點定位技術已經得到了大量的驗證，其定位準確度與高精度差分定位技術相當[4-6]。但目前對于動態精密單點定位技術在實地的應用研究較少，大部分是基于靜態模擬動態[7]。基于上述情況，本文對動態精密單點定位技術的準確度進行實地研究，并根據相關結果分析得出相應的結論。

1 動態精密單點定位原理

衛星信號在傳播的過程中會涉及到許多誤差因素的影響，那么接收到的觀測量必須對這些誤差加以修正，這些誤差主要包括：衛星天線相位中心、衛星端天線相位轉繞、相對論效應、電離層延遲、對流層延遲、接收機天線相位中心和地球自轉。忽略部分誤差，簡化后基本的碼和相位觀測量方程如下[8]：

式（1）中，P表示偽距觀測量，L表示轉化成距離的相位觀測量，下標1和2表示不同頻率，I表示電離層延遲;Trop表示對流層延遲;N則表示模糊度;f表示頻率;λ表示對應頻率波長;tr與ts分別表示接收機和衛星鐘差，其中衛星鐘差采用IGS 30s產品;c表示光速;ρ表示幾何距離，其隱含的衛星軌道坐標也由IGS精密產品提供。

為方便消電離觀測量進行解算，則需要對其進行線性化。經過線性化后，等式左邊為已知量，等式右邊則是關于待求參數的線性表達式，每個歷元待求參數可以用下述公式表示：

式中xk，yk，zk分別表示k時刻需求的位置參數，dt表示接收機鐘差，ztd表示對流層天頂延遲，N表示對應衛星的模糊度參數，1至m表示衛星。

利用最小二乘或者卡爾曼濾波均可對線性化后的等式進行求解，這里僅列舉采用卡爾曼濾波的解算步驟。標準的卡爾曼濾波包含2個步驟，分別為預測和更新，如下式[9]：

其中上標為“-”的表示預測;X表示待求的參數;Ф表示上個時刻到當前時刻的狀態轉移，對于動態精密單點定位可將該矩陣設置為單位陣;w為未考慮的誤差;P表示協方差陣，初始歷元協方差陣由經驗值確定，后續則根據卡爾曼濾波進行傳遞;Q表示過程噪聲，對于模糊度如不發生周跳則為一常數，故其過程噪聲為0，對流層過程噪聲可設置為1cm/sqrt（hour），對于位置和接收機鐘差參數則可設置較大的噪聲;K表示增益;H表示待求參數的系數陣R表示觀測量的測量噪聲矩陣，測量噪聲主要與高度角相關，偽距和相位噪聲比值設為100∶1;Z表示上述消電離層觀測量線性化后的等式左邊;I表示階數與待求參數個數相同的單位矩陣。

2 試驗數據及方案

數據采集工作于2020年3月進行。為與RTK進行比較，總共利用3臺GNSS接收機，其中基站采用LEICA GX1230接收機，流動站接收機則均采用LEICA GS15接收機，3臺接收機天線均為LEIAX1202GG型內置天線。基站架設于新建銀西鐵路的CPI控制點上，流動站則在附近先靜止后運動，運動過程中隨機反復，最后又回到原地，采樣率均為15秒。其中LEICA GX1230接收機只能接收GPS信號觀測量，LEICA GS15接收機則能同時接收GPS和GLONASS信號觀測量。為獲取基站的準確位置，基站接收機觀測時間約為2小時，其坐標由高精度軟件靜態解算得到，并與往期的坐標進行比較。在差分解算時將基站坐標作為已知值，解算出流動站的坐標，這一過程利用LGO軟件完成。同時利用西南交大PLAOD軟件進行動態解算流動站的坐標，PLAOD軟件所有解算均為非差模式，里面包含動態精密單點定位模塊[10]。

3 解算結果及分析

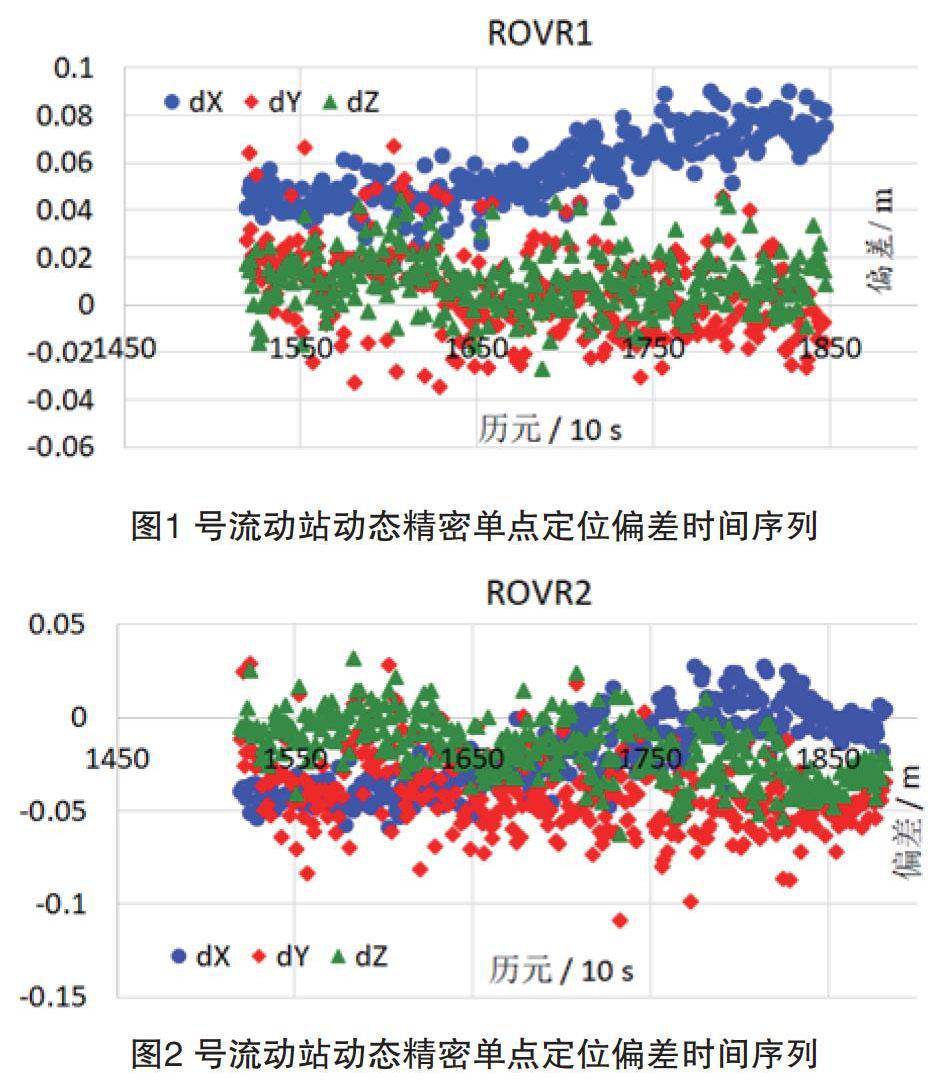
首先利用PLAOD解算兩個流動站的GPS觀測量，確保觀測時段內兩個流動站可以共視衛星顆數均大于設定的最小閾值（5顆），且衛星的高度角均大于15°為驗證其定位精度，將LGO解算的流動站結果作為真值，將PLAOD解算結果與其作差，結果如圖1、圖2所示。

從圖1、圖2可以看出利用動態精密單點定位解算的結果大部分歷元達到了厘米級結果，極個別的歷元超出了1dm的限制。

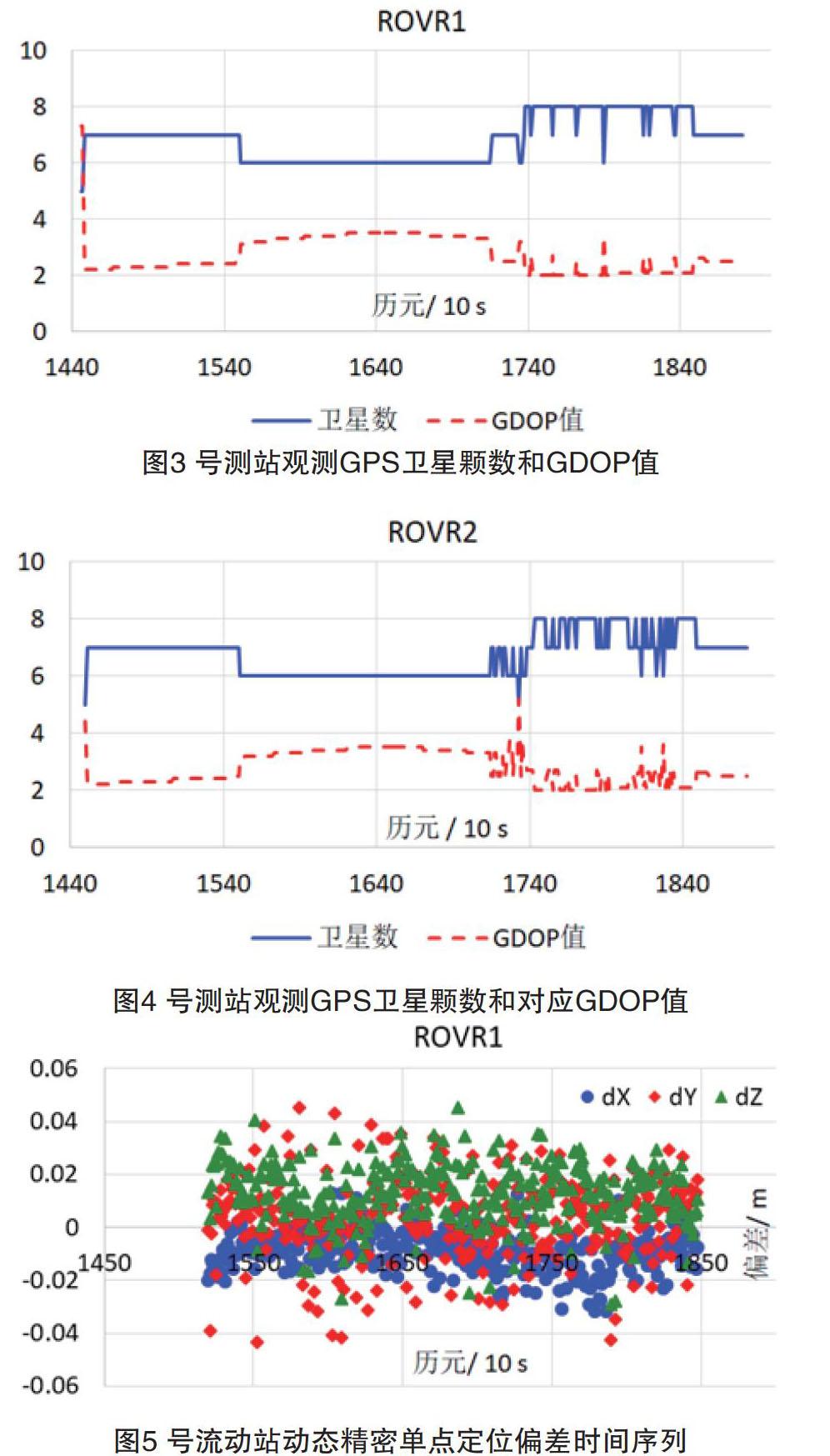
進一步分析其衛星的幾何分布和DOP值，如圖3和4所示。

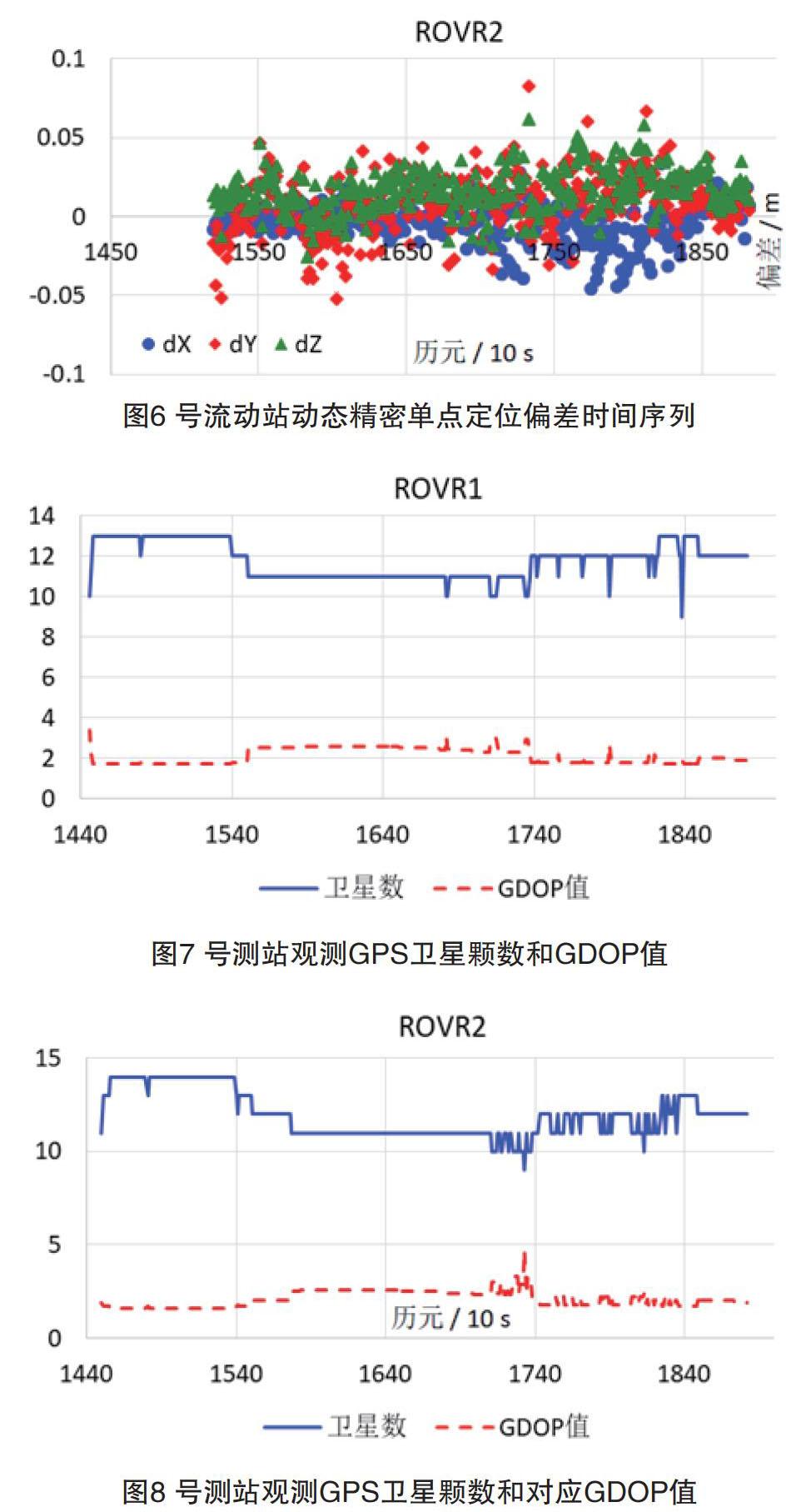
從圖3、圖4可以看出，衛星在接收機靜止時鎖定的GPS衛星顆數比較穩定，其對應的GDOP值也比較穩定。當接收機處于運動時，其鎖定的衛星顆數存在一定的波動，同時對應的GDOP值也波動頻繁。衛星發生升降不僅會影響GDOP值，同時會影響模糊度的估計，因為模糊度可能需要重新初始化，重新收斂需要一定的時間。基于這些因素，解算融合GLONASS和GPS觀測量的動態精密單點定位結果如圖5、圖6所示。

從圖5、圖6圖看，加入GLONASS衛星觀測量后，定位結果得到了較大的改善，大部分方向偏差均在5cm以內， 2號流動站有極少數歷元的方向偏差超過了5cm，但均在1dm以內。融合GPS和GLONASS后的衛星顆數和GDOP值如圖7和8所示。

4 結論

通過上述實驗分析發現，利用動態精密單點定位技術能獲取厘米級的定位準確度，尤其是利用GPS+GLONASS雙系統，每個方向上大多能獲取±5cm的準確度。通過后續分析發現，平面定位精度較高，而主要偏差則體現在高程方向。這也意味著利用動態精密單點定位在鐵路建設行業進行勘測等工作是具備可行性的，同時多星座系統的組合解算，也會對定位精度有很好的提升。

參考文獻

[1] 徐紹銓，張華海，楊志強，等.GPS測量原理及應用[M].武漢：武漢大學出版社，2002.

[2] 黃丁發，熊永良，袁林果.全球定位系統（GPS）-理論與實踐 [M].成都：西南交通大學出版社，2006.

[3] 張廣發.GPS-RTK定位技術在礦山測量中應用及優缺點的探討[J].西部探礦工程，2014，26（03）：145-146+150.

[4] Zumberge， J. F.， M. B. Heflin， D. C. Jefferson， et al. Precise Point Processing for the Efficient and Robust Analysis of GPS Data from Large Networks[J].J. Geophys. Res.，1997，102（B3）：5005-5017.

[5] Kouba J， Heroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J].GPS Solut，2001，5：12-28.

[6] 韓保民，歐吉坤.基于GPS非差觀測值進行精密單點定位研究[J].武漢大學學報（信息科學版），2003，28（4）：409-412.

[7] 任曉東，張柯柯，李星星，等.BeiDou、Galileo、GLONASS、GPS多系統融合精密單點[J].測繪學報，2015，44（12）：1307-1313.

[8] Jan Kouba.A Guide To Using International GNSS Service （IGS） Products[EB/OL].（2009-04-23）[2019-01-15].http：//igscb.jpl.nasa.gov/igscb/resource/pubs/usingig-sproductsver21.

[9] Welch G，Bishop G.An Introduction to the Kalman Filter[M].University of North Carolina at Chapel Hill，2001.

[10] Xu Shaoguang， Xiong Yongliang， Liu Ning， et al.? Status and Progress of PLAOD[C].International Symposium on GPS/GNSS 2012，Xian，China.2012-10-31.